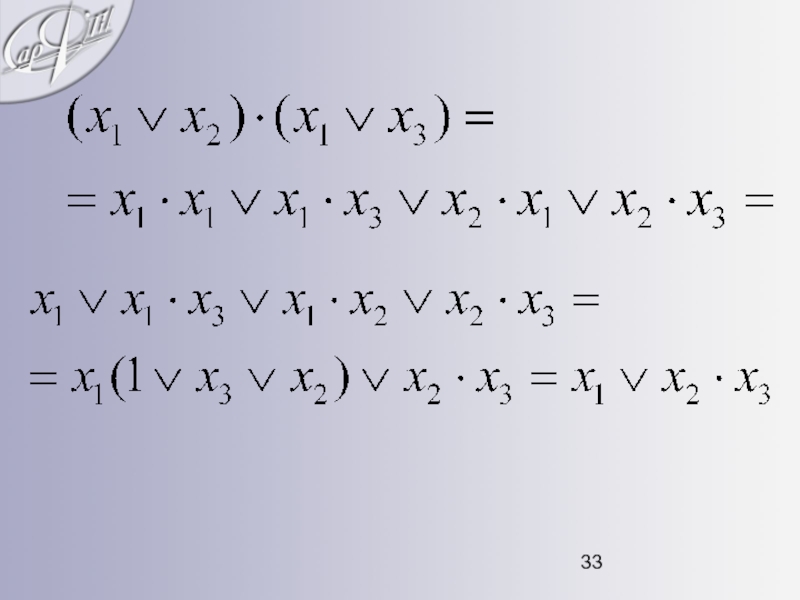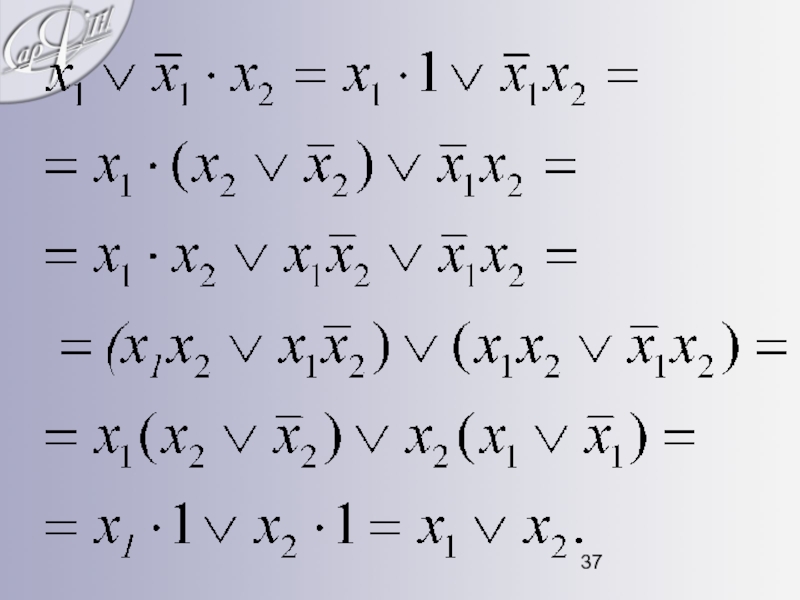- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Элементы алгебры логики презентация
Содержание
- 1. Элементы алгебры логики
- 2. Понятие цифрового автомата цифровым автоматом называется устройство,
- 3. различают автоматы синхронного и асинхронного действия.
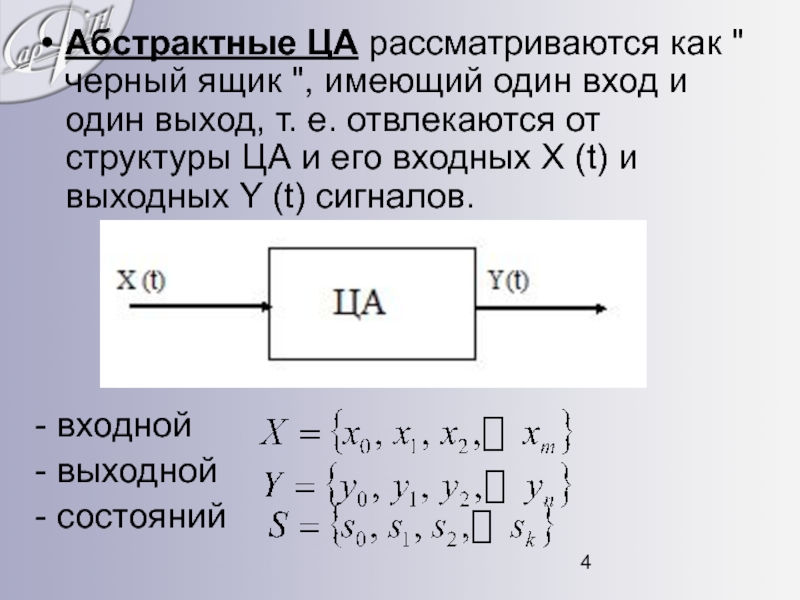
- 4. Абстрактные ЦА рассматриваются как " черный ящик
- 5. Тогда закон функционирования абстрактного автомата может быть
- 6. ЦА, выходные сигналы в которых зависят только
- 7. ЦА, имеющая более одного внутреннего состояния, называются
- 8. Функции алгебры логики и их основные свойства.
- 9. 3. Логическая функция ( функция алгебры логики
- 10. 5. Если две ФАЛ
- 11. 7. ФАЛ называют не полностью определенными или
- 12. Теорема: Число различных ФАЛ, зависящих
- 13. Теорема: Число ФАЛ, существенно зависящих от n
- 14. Правая часть соотношения есть разность между числом
- 15. Пример: Найти число ФАЛ, существенно зависящих
- 16. Элементарные функции алгебры логики n=1. Число
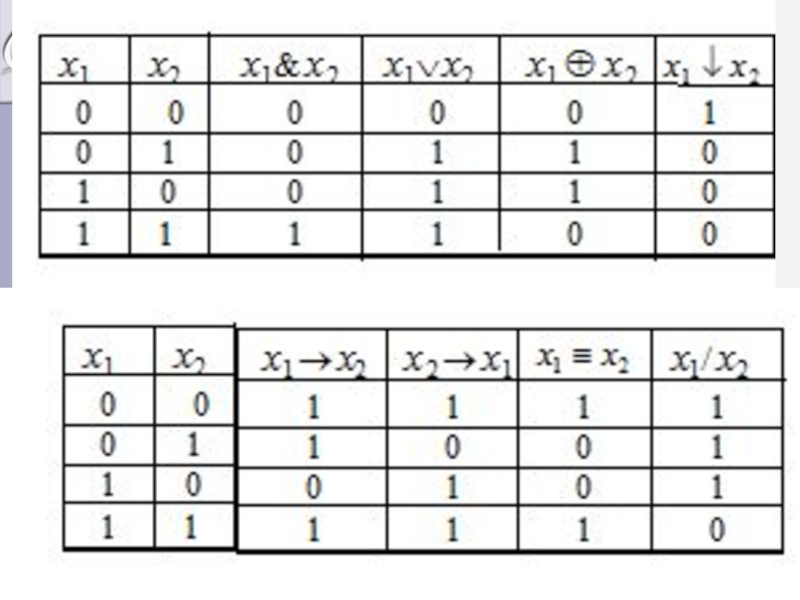
- 17. Элементарные ФАЛ 2-х переменных n=2; Число ФАЛ равно 16.
- 19. конъюнкция (логическое умножение, или функция И) истинна
- 20. дизъюнкция (логическое сложение, или функция ИЛИ) истинна
- 21. 3. Функция сложения по модулю 2
- 22. 4. функция равнозначности, которая истинна тогда и
- 23. 5. импликация х1 в х2 ложна
- 24. 6. функция Пирса ( Вебба ) истинна
- 25. 7. Функция Шеффера ложна только тогда
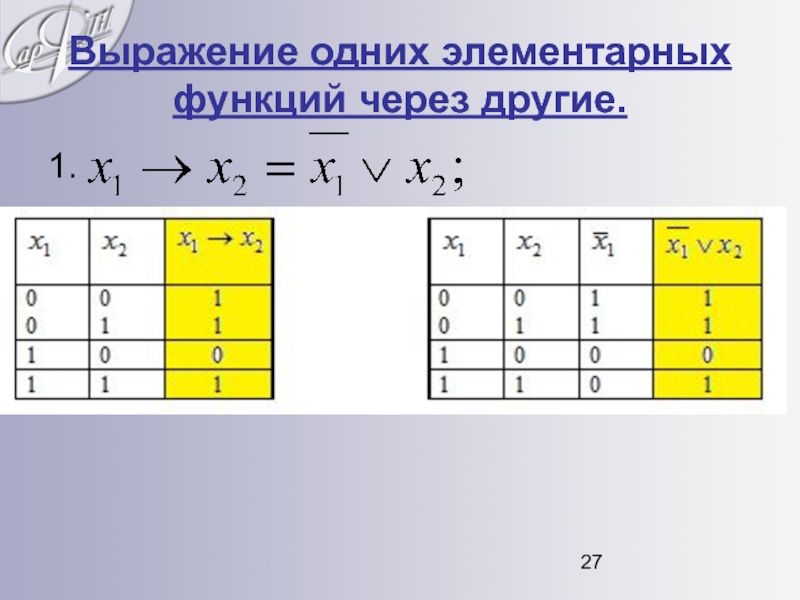
- 27. Выражение одних элементарных функций через другие. 1.
- 28. 2. 3.
- 29. 4. 5.
- 30. Свойства элементарных ФАЛ.
- 31. Свойства конъюнкции, дизъюнкции, отрицания Свойство ассоциативности (сочетательный
- 32. 3. Свойство дистрибутивности (распределительный закон): для конъюнкции
- 34. Законы Де-Моргана: 1. 2.
- 35. Законы (правила) поглощения: 1. 2.
- 36. Из логических функций устанавливается правило склеивания: правило вычеркивания:
- 38. Знание свойств, законов и правил элементарных
- 39. Свойства функции сложения по модулю два
- 40. ассоциативности (сочетательный закон): дистрибутивности (распределительный
- 41. Функции НЕ, ИЛИ, НЕ могут быть
- 42. Свойства функции импликации Для функции
- 43. Функции НЕ, ИЛИ, И выражаются через импликацию следующим образом:
Понятие цифрового автомата цифровым автоматом называется устройство, предназначенное для преобразования цифровой (дискретной) информации, способное переходить под воздействием входных сигналов из одного состояния в другие и выдавать выходные сигналы. Отличительные особенности
Слайд 1Саровский физико-технический институт
Национального исследовательского ядерного университета МИФИ
Элементы алгебры логики
Алексеев В.В.
Саров
2016
Слайд 2Понятие цифрового автомата
цифровым автоматом называется устройство, предназначенное для преобразования цифровой (дискретной)
информации, способное переходить под воздействием входных сигналов из одного состояния в другие и выдавать выходные сигналы.
Отличительные особенности ЦА заключаются в том, что они имеют дискретное множество внутренних состояний и переход из одного в другое осуществляется скачкообразно.
Отличительные особенности ЦА заключаются в том, что они имеют дискретное множество внутренних состояний и переход из одного в другое осуществляется скачкообразно.
Слайд 3различают автоматы синхронного и асинхронного действия.
Для идеализированных ЦА не учитывается
переходные процессы в схемах и разница в фактических величинах Т для правильного функционирования не имеет значение.
По степени детализации описания ЦА различают автоматы абстрактные и структурные. В соответствии с этим различают абстрактную и структурную теорию ЦА.
По степени детализации описания ЦА различают автоматы абстрактные и структурные. В соответствии с этим различают абстрактную и структурную теорию ЦА.
Слайд 4Абстрактные ЦА рассматриваются как " черный ящик ", имеющий один вход
и один выход, т. е. отвлекаются от структуры ЦА и его входных Х (t) и выходных Y (t) сигналов.
- входной
- выходной
- состояний
- входной
- выходной
- состояний
Слайд 5Тогда закон функционирования абстрактного автомата может быть задан уравнениями:
(1)
- где ƒ (s, x) - функция переходов
автомата ;
p (x, s) - функция выходов автомата ;
s0- начальное состояние автомата .
(Автомат Мили)
- где ƒ (s, x) - функция переходов
автомата ;
p (x, s) - функция выходов автомата ;
s0- начальное состояние автомата .
(Автомат Мили)
Слайд 6ЦА, выходные сигналы в которых зависят только от состояния автомата и
не зависят от значения входных сигналов, называются автоматами Мура
(2)
где μ [ s (t) ] -сдвинутая функция выхода.
(2)
где μ [ s (t) ] -сдвинутая функция выхода.
Слайд 7ЦА, имеющая более одного внутреннего состояния, называются автоматами с памятью. Частный
случай абстрактных ЦА - автоматы с одним внутренним состоянием. Такие тривиальные автоматы называют автоматами без памяти или комбинационными схемами. Закон функционирования таких автоматов будет определяться одним уравнением:
Y (t) = ƒ [ x(t)]
Y (t) = ƒ [ x(t)]
Слайд 8Функции алгебры логики и их основные свойства.
Основные
определения
Основное понятие АЛ - высказывание. Высказывание - некоторое предложение, о котором можно утверждать, что оно истинно или ложно.
Логическая (Булева) переменная - такая величина X, которая может принимать только два значения:
X = { 0, 1 }.
Основное понятие АЛ - высказывание. Высказывание - некоторое предложение, о котором можно утверждать, что оно истинно или ложно.
Логическая (Булева) переменная - такая величина X, которая может принимать только два значения:
X = { 0, 1 }.
Слайд 93. Логическая функция ( функция алгебры логики - ФАЛ ) -
функция
ƒ , принимающая значение, равное нулю или единице на наборе логических переменных .
Пусть и
4. Функцией алгебры логики (ФАЛ) называется функция, дающая однозначное отображение X в Y, т.е.
ƒ , принимающая значение, равное нулю или единице на наборе логических переменных .
Пусть и
4. Функцией алгебры логики (ФАЛ) называется функция, дающая однозначное отображение X в Y, т.е.
Слайд 105. Если две ФАЛ
и принимают на всех возможных наборах значений аргументов одинаковые значения, то функции ƒ1 и ƒ2 называются равносильными (равными), т.е.:
=
6. Функция существенно зависит от аргумента , если имеет место соотношение:
=
6. Функция существенно зависит от аргумента , если имеет место соотношение:
Слайд 117. ФАЛ называют не полностью определенными или не- доопределенными, если на
некоторых наборах значения ФАЛ не определены.
Если ФАЛ не определена на m наборах аргументов, то путем ее произвольного доопределения можно получить 2m различных полностью определенных функций.
Если ФАЛ не определена на m наборах аргументов, то путем ее произвольного доопределения можно получить 2m различных полностью определенных функций.
Слайд 13Теорема:
Число ФАЛ, существенно зависящих от n аргументов, определяется следующим рекуррентным соотношением:
где Аi - число ФАЛ, существенно зависящих от i аргументов,
Слайд 14Правая часть соотношения есть разность между числом всех ФАЛ и суммой
всех ФАЛ, существенно зависящих от любого числа аргументов, меньших чем n.
Вместо рекуррентного соотношения можно найти прямое выражение для значений:
Вместо рекуррентного соотношения можно найти прямое выражение для значений:
Слайд 19конъюнкция (логическое умножение, или функция И) истинна тогда и только тогда,
когда и x1 и x2 истинны.
1.
Слайд 20дизъюнкция (логическое сложение, или функция ИЛИ) истинна тогда, и только тогда,
когда истинны или x1, или x2, или обе переменные.
2.
Слайд 213.
Функция сложения по модулю 2 (или функция разноименности, или
функция исключающее ИЛИ) истинна тогда и только тогда когда x1≠x2.
Слайд 224.
функция равнозначности, которая истинна тогда и только тогда, когда обе переменные
или истинны, или ложны.
Слайд 31Свойства конъюнкции, дизъюнкции, отрицания
Свойство ассоциативности (сочетательный закон):
Свойство коммутативности (переместительный закон):
;
Слайд 323. Свойство дистрибутивности (распределительный закон):
для конъюнкции относительно дизъюнкции:
для дизъюнкции относительно конъюнкции:
Действительно:
Слайд 38
Знание свойств, законов и правил элементарных ФАЛ необходимо для аналитического описания
функций алгебры логики, их преобразований.
Слайд 39Свойства функции сложения по модулю два
Функция сложения по модулю два
обладает следующими свойствами:
коммутативности (переместительный закон)
коммутативности (переместительный закон)
Слайд 40ассоциативности (сочетательный закон):
дистрибутивности (распределительный закон):
справедливы правила:
Слайд 41
Функции НЕ, ИЛИ, НЕ могут быть выражены через функцию сложения по
модулю два следующим образом:
