- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
ЕГЭ информатика, задания А1 и А2 презентация
Содержание
- 1. ЕГЭ информатика, задания А1 и А2
- 2. Источники kpolyakov.spb.ru inf-ege.sdamgia.ru ctege.info/informatika-teoriya-ege/
- 3. Задание А1 Различные системы счисления Развернутая форма
- 4. Свойства чисел в двоичной системе счисления четные
- 5. Пример задачи Дано: a=D816 и b=3328.
- 6. Задание А2 Построение таблиц истинности логических выражений
- 7. Понятие алгебры логики Основные понятия В
- 8. Операции алгебры логики Базовыми элементами, которыми оперирует
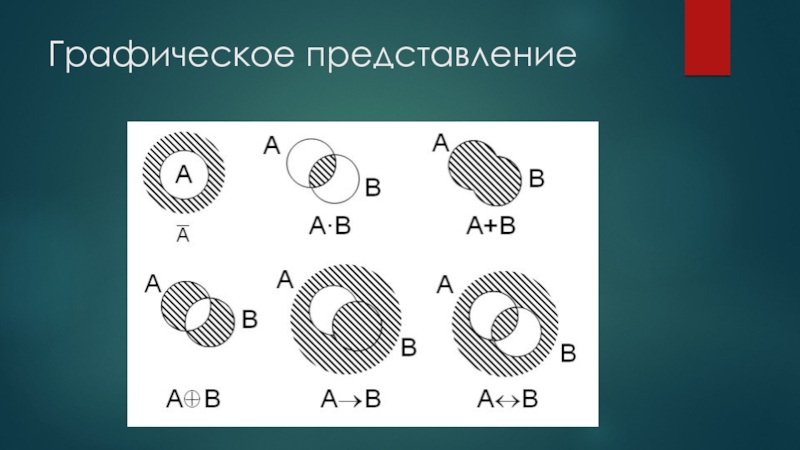
- 9. Графическое представление
- 10. Примеры задач
Слайд 3Задание А1
Различные системы счисления
Развернутая форма записи числа
Когда мы записываем число
в десятичной системе счисления (q=10), мы как бы раскладываем его в сумму единиц, десяток, сотен, тысяч и т.д., при этом количество в каждом разряде строго меньше 10.
Число x в q-ричной системе счисления представляется также в виде суммы целых степеней числа q с коэффициентами: an−1⋅q^(n−1)+an−2⋅q^(n−2)+⋯+a1⋅q^1+a0⋅q^0
Перевод в десятичную систему счисления осуществляется прямым вычислением по этой формуле.
Число x в q-ричной системе счисления представляется также в виде суммы целых степеней числа q с коэффициентами: an−1⋅q^(n−1)+an−2⋅q^(n−2)+⋯+a1⋅q^1+a0⋅q^0
Перевод в десятичную систему счисления осуществляется прямым вычислением по этой формуле.
Слайд 4Свойства чисел в двоичной системе счисления
четные числа оканчиваются на 0
нечетные –
на 1;
числа, которые делятся на 4, оканчиваются на 00; …; числа, которые делятся на 2k, оканчиваются на k нулей.
числа вида 2k записываются в двоичной системе как единица и k нулей, например: 16=24=10000;
числа вида 2k−1 записываются в двоичной системе k единицами, например: 15=24−1=1111; • если число N принадлежит интервалу 2k−1≤N
числа, которые делятся на 4, оканчиваются на 00; …; числа, которые делятся на 2k, оканчиваются на k нулей.
числа вида 2k записываются в двоичной системе как единица и k нулей, например: 16=24=10000;
числа вида 2k−1 записываются в двоичной системе k единицами, например: 15=24−1=1111; • если число N принадлежит интервалу 2k−1≤N
Слайд 5Пример задачи
Дано: a=D816 и b=3328.
Какое из чисел с, записанных в
двоичной системе счисления, удовлетворяет неравенству a1. 110110012
2. 110111002
3. 110101112
4. 110110012
2. 110111002
3. 110101112
4. 110110012
Слайд 6Задание А2
Построение таблиц истинности логических выражений
Типы задач:
Частично заполненные таблицы истинности логических
выражений
Логические выражения, содержащие более трёх переменных
Логические выражения, содержащие три переменные
Логические выражения, содержащие более трёх переменных
Логические выражения, содержащие три переменные
Слайд 7Понятие алгебры логики
Основные понятия
В основе теории множеств лежат первичные понятия:
множество и отношение быть элементом множества (обозначается как x∈A - «x есть элемент множества A»).
Над множествами определены следующие операции:
• объединение (или сумма) (обозначается как A∪B );
• пересечение (или произведение) (обозначается как A∩B );
• разность (обозначается как A∖B, реже A−B );
• симметрическая разность (обозначается как A△B).
Для множеств определены следующие бинарные отношения:
• отношение равенства (обозначается как A=B );
• отношение включения (обозначается как A⊂B )
Над множествами определены следующие операции:
• объединение (или сумма) (обозначается как A∪B );
• пересечение (или произведение) (обозначается как A∩B );
• разность (обозначается как A∖B, реже A−B );
• симметрическая разность (обозначается как A△B).
Для множеств определены следующие бинарные отношения:
• отношение равенства (обозначается как A=B );
• отношение включения (обозначается как A⊂B )
Слайд 8Операции алгебры логики
Базовыми элементами, которыми оперирует алгебра логики, являются высказывания. Высказывания
обозначают строчными буквами — логическими переменными. Возможные значения логической переменной: 1 — истина, 0 — ложь. Высказывания строятся из логических переменных и логических констант 1 и 0 при помощи операций:
¬ — отрицание (унарная операция),
∧ — конъюнкция, логическое умножение (бинарная),
∨ — дизъюнкция, логическое сложение (бинарная),
↔ — эквивалентность («тогда и только тогда, когда») (бинарная),
→ — импликация («следовательно») (бинарная),
⊕ — сложение по модулю два («исключающее или»), (¬А∧B)∨(A∧¬B)
| — штрих Шеффера, (¬А∨¬B)
↓ — стрелка Пирса и другие. (¬А∧¬B)
Приоритет логических операций: если в выражении нет скобок, сначала выполняются все операции «НЕ», затем – «И», затем – «ИЛИ», и самая последняя – «импликация»
¬ — отрицание (унарная операция),
∧ — конъюнкция, логическое умножение (бинарная),
∨ — дизъюнкция, логическое сложение (бинарная),
↔ — эквивалентность («тогда и только тогда, когда») (бинарная),
→ — импликация («следовательно») (бинарная),
⊕ — сложение по модулю два («исключающее или»), (¬А∧B)∨(A∧¬B)
| — штрих Шеффера, (¬А∨¬B)
↓ — стрелка Пирса и другие. (¬А∧¬B)
Приоритет логических операций: если в выражении нет скобок, сначала выполняются все операции «НЕ», затем – «И», затем – «ИЛИ», и самая последняя – «импликация»