- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Эффективное кодирование сообщений презентация
Содержание
- 1. Эффективное кодирование сообщений
- 2. ПОСТАНОВКА ЗАДАЧИ КОДИРОВАНИЯ ИСТОЧНИКА При кодировании, в
- 3. ПОСТАНОВКА ЗАДАЧИ КОДИРОВАНИЯ ИСТОЧНИКА Типы кодирования источника:
- 4. БАЗОВЫЕ СТРАТЕГИИ КОМПРЕССИИ ДАННЫХ 1. Статистическое кодирование:
- 5. КОДОВЫЕ СЛОВА ФИКСИРОВАННОЙ ДЛИНЫ Блоковое кодирование сопоставляет
- 6. КОДОВЫЕ СЛОВА ФИКСИРОВАННОЙ ДЛИНЫ Пример. Передача числового
- 7. НЕРАВНОМЕРНЫЕ КОДЫ Применение: при неравных вероятностях сообщений
- 8. НЕРАВНОМЕРНЫЕ КОДЫ Префиксному коду сопоставляется бинарное ориентированное
- 9. НЕРАВНОМЕРНЫЕ КОДЫ Обобщенная теорема кодирования источника: Дискретный
- 10. КОДИРОВАНИЕ ИСТОЧНИКОВ БЕЗ ПАМЯТИ Метод Шеннона Расположим
- 11. КОДИРОВАНИЕ ИСТОЧНИКОВ БЕЗ ПАМЯТИ Метод Шеннона
- 12. КОДИРОВАНИЕ ИСТОЧНИКОВ БЕЗ ПАМЯТИ Статический метод Хаффмана
- 13. КОДИРОВАНИЕ ИСТОЧНИКОВ БЕЗ ПАМЯТИ Статический метод Хаффмана
- 14. КОДИРОВАНИЕ ИСТОЧНИКОВ БЕЗ ПАМЯТИ Статический метод Хаффмана
- 15. КОДИРОВАНИЕ ИСТОЧНИКОВ БЕЗ ПАМЯТИ Адаптивный метод Хаффмана
- 16. КОДИРОВАНИЕ ИСТОЧНИКОВ БЕЗ ПАМЯТИ Адаптивный метод Хаффмана
- 17. КОДИРОВАНИЕ ИСТОЧНИКОВ БЕЗ ПАМЯТИ Адаптивный метод Хаффмана
- 18. КОДИРОВАНИЕ ИСТОЧНИКОВ БЕЗ ПАМЯТИ Адаптивный метод Хаффмана
- 19. КОДИРОВАНИЕ ИСТОЧНИКОВ БЕЗ ПАМЯТИ Метод Хаффмана
- 20. КОДИРОВАНИЕ ИСТОЧНИКОВ БЕЗ ПАМЯТИ Арифметическое кодирование
- 21. КОДИРОВАНИЕ ИСТОЧНИКОВ БЕЗ ПАМЯТИ Арифметическое кодирование
- 22. КОДИРОВАНИЕ ИСТОЧНИКОВ БЕЗ ПАМЯТИ Арифметическое кодирование
- 23. КОДИРОВАНИЕ ИСТОЧНИКОВ БЕЗ ПАМЯТИ Арифметическое кодирование. Целочисленная реализация
- 24. КОДИРОВАНИЕ ИСТОЧНИКОВ БЕЗ ПАМЯТИ
- 25. КОДИРОВАНИЕ ИСТОЧНИКОВ БЕЗ ПАМЯТИ Арифметическое кодирование. Декодер
- 26. КОДИРОВАНИЕ ИСТОЧНИКОВ БЕЗ ПАМЯТИ Integer Coding (целочисленное
- 27. КОДИРОВАНИЕ ИСТОЧНИКОВ БЕЗ ПАМЯТИ Integer Coding
- 28. КОДИРОВАНИЕ ИСТОЧНИКОВ БЕЗ ПАМЯТИ Коды Элайеса
- 29. КОДИРОВАНИЕ ИСТОЧНИКОВ БЕЗ ПАМЯТИ Коды Элайеса
- 30. КОДИРОВАНИЕ ИСТОЧНИКОВ БЕЗ ПАМЯТИ Еще один вариант
- 31. КОДИРОВАНИЕ ИСТОЧНИКОВ БЕЗ ПАМЯТИ Код Левенштейна
- 32. КОДИРОВАНИЕ ИСТОЧНИКОВ С ПАМЯТЬЮ Кодирование длин серий
- 33. КОДИРОВАНИЕ ИСТОЧНИКОВ С ПАМЯТЬЮ Словарное сжатие
- 34. КОДИРОВАНИЕ ИСТОЧНИКОВ С ПАМЯТЬЮ Алгоритм LZ77
- 35. КОДИРОВАНИЕ ИСТОЧНИКОВ С ПАМЯТЬЮ Алгоритм LZ77. Сжатие
- 36. КОДИРОВАНИЕ ИСТОЧНИКОВ С ПАМЯТЬЮ Алгоритм LZSS
- 37. Алгоритм LZSS. Сжатие фразы "кот_ломом_колол_слона"
- 38. КОДИРОВАНИЕ ИСТОЧНИКОВ С ПАМЯТЬЮ Алгоритм LZ78
- 39. КОДИРОВАНИЕ ИСТОЧНИКОВ С ПАМЯТЬЮ Алгоритм LZ78. Сжатие
- 40. ПРЕОБРАЗОВАНИЕ БЛОКОВ ДАННЫХ Преобразование Барроуза-Уиллера (BWT)
- 41. ПРЕОБРАЗОВАНИЕ БЛОКОВ ДАННЫХ Преобразование Барроуза-Уиллера (BWT)
- 42. ПРЕОБРАЗОВАНИЕ БЛОКОВ ДАННЫХ Преобразование Барроуза-Уиллера (BWT)
- 43. ПРЕОБРАЗОВАНИЕ БЛОКОВ ДАННЫХ Преобразование Барроуза-Уиллера (BWT)
- 44. ПРЕОБРАЗОВАНИЕ БЛОКОВ ДАННЫХ Преобразование Барроуза-Уиллера (BWT)
- 45. МЕТОДЫ АНАЛИЗА (СРАВНЕНИЯ) АЛГОРИТМОВ КОМПРЕССИИ Наборы тестовых
Слайд 1ЭФФЕКТИВНОЕ КОДИРОВАНИЕ СООБЩЕНИЙ
Постановка задачи кодирования источника
Базовые стратегии компрессии данных
Кодовые слова фиксированной
Неравномерные коды
Методы оптимального кодирования без памяти
Методы трансформации данных
Методики сравнения алгоритмов. Наборы тестовых данных
Слайд 2ПОСТАНОВКА ЗАДАЧИ КОДИРОВАНИЯ ИСТОЧНИКА
При кодировании, в соответствии с определенным правилом (кодом)
f : U* → X*,
а код последовательности ui или кодовое слово xi – как xi = f(ui).
Слайд 3ПОСТАНОВКА ЗАДАЧИ КОДИРОВАНИЯ ИСТОЧНИКА
Типы кодирования источника:
- слова источника ui различной длины
- слова источника ui одинаковой длины ni=n=const -> кодовые слова xi одинаковой длины ki=k=const;
- слова источника ui одинаковой длины ni=n=const -> кодовые слова xi различной длины ki;
- слова источника переменной длины ui -> кодовые слова xi переменной длины ki.
Коды фиксированной длины
Коды переменной длины
Эффективное кодирование обеспечивает увеличение средней информационной нагрузки на кодовое слово (символ кодового словаря).
Слайд 4БАЗОВЫЕ СТРАТЕГИИ КОМПРЕССИИ ДАННЫХ
1. Статистическое кодирование:
- блочное, когда статистика хранится
- поточное, когда статистика постоянно обновляется
2. Трансформация потока (словарные методы)
3. Трансформация блока
Слайд 5КОДОВЫЕ СЛОВА ФИКСИРОВАННОЙ ДЛИНЫ
Блоковое кодирование сопоставляет уникальную последовательность из R кодовых
Число двоичных символов кодера на один символ источника
R=[log2L]+1.
Поскольку H(X)≤log2L, то R≥H(X). Эффективность кодирования определяется отношением H(X)/R.
Если L равно степени 2 и символы источника равновероятны, то R=H(X).
Если L не является степенью 2, но символы источника все еще равновероятны, R отличается от H(X) самое большее на 1 символ.
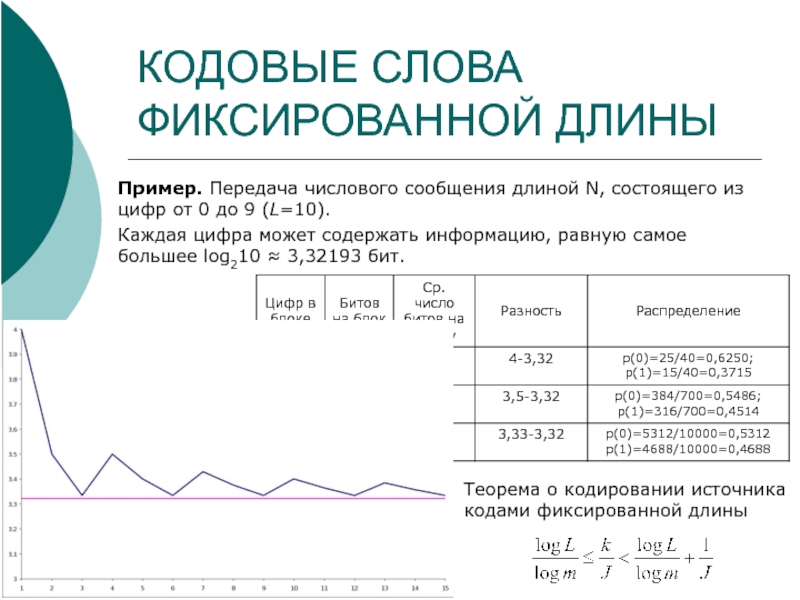
Слайд 6КОДОВЫЕ СЛОВА ФИКСИРОВАННОЙ ДЛИНЫ
Пример. Передача числового сообщения длиной N, состоящего из
Каждая цифра может содержать информацию, равную самое большее log210 ≈ 3,32193 бит.
Теорема о кодировании источника кодами фиксированной длины
Слайд 7НЕРАВНОМЕРНЫЕ КОДЫ
Применение:
при неравных вероятностях сообщений источника.
Требования к кодам переменной длины:
- свойство
- отсутствие префикса (возможность мгновенного декодирования).
Условие существование мгновенного кода – неравенство Крафта:
Необходимое и достаточное условие для существования двоичного кода с кодовыми символами длины k1≤k2≤...≤kL, удовлетворяющего условию отсутствия префикса
или
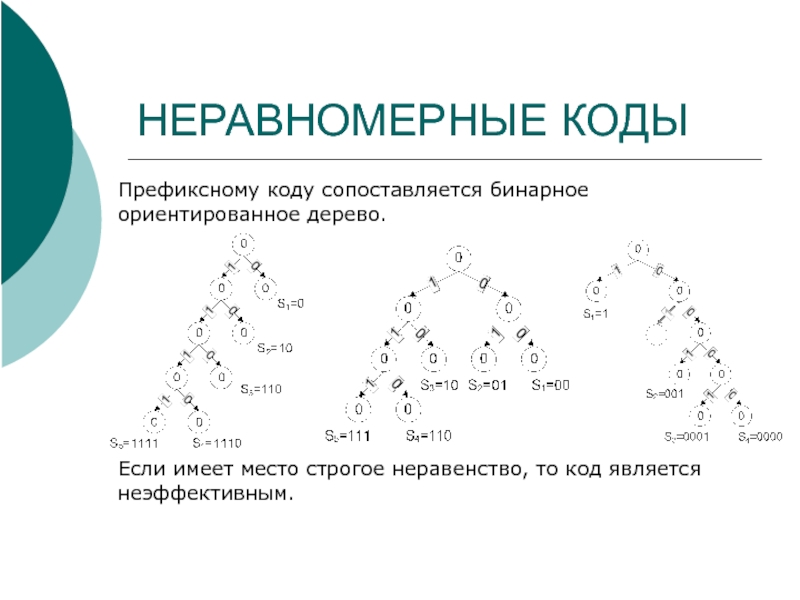
Слайд 8НЕРАВНОМЕРНЫЕ КОДЫ
Префиксному коду сопоставляется бинарное ориентированное дерево.
Если имеет место строгое неравенство,
Слайд 9НЕРАВНОМЕРНЫЕ КОДЫ
Обобщенная теорема кодирования источника:
Дискретный источник без памяти U имеет алфавит
Обозначим через m количество возможных символов в кодовом алфавите, а ki – число букв в кодовом слове, соответствующем ai. Тогда среднее число букв в кодовом слове на одну букву источника будет определяться как
При заданном конечном ансамбле источника U с энтропией H(U) и кодовом алфавите из m символов существует возможность создать код, который отвечает префиксному требованию условию и имеет среднюю длину, удовлетворяющую условию
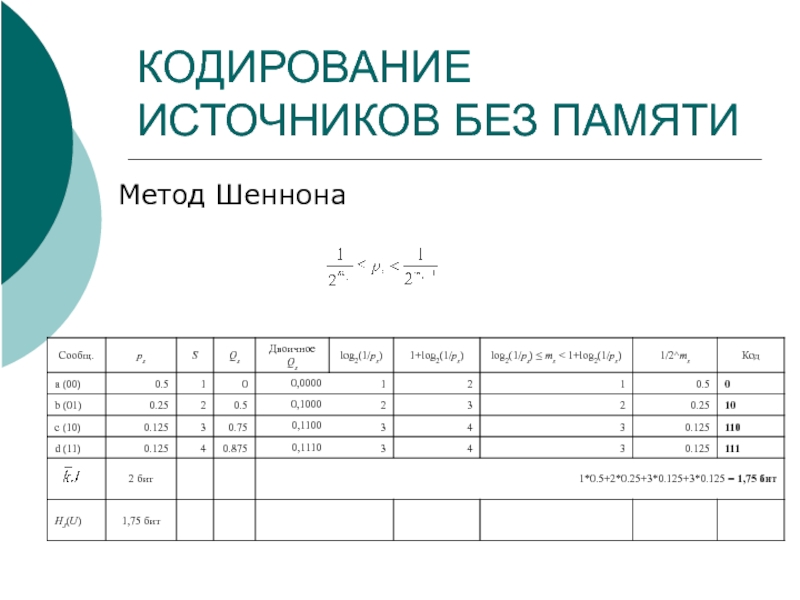
Слайд 10КОДИРОВАНИЕ ИСТОЧНИКОВ БЕЗ ПАМЯТИ
Метод Шеннона
Расположим все сообщения ui длиной J в
Слайд 12КОДИРОВАНИЕ ИСТОЧНИКОВ БЕЗ ПАМЯТИ
Статический метод Хаффмана
Лемма. Пусть вероятности букв (символов) алфавита
p(a1) ≥ p(a2) ≥... ≥ p(aL).
Тогда существует оптимальный код, длина слов которого не убывают, а две наименее вероятные буквы имеют коды одинаковой длины:
|f(a1)| ≤ |f(a2)| ≤ ... ≤ |f(aL-1)| = |f(aL)|.
Слайд 13КОДИРОВАНИЕ ИСТОЧНИКОВ БЕЗ ПАМЯТИ
Статический метод Хаффмана
Пример построения дерева Хаффмана (H-дерева).
Средняя длина
0,3*2+0,2*2+0,15*3+0,15*3+0,1*3+0,1*3= 0,6+0,4+0,45+0,45+0,3+0,3=1+0,9+0,6=2,5).
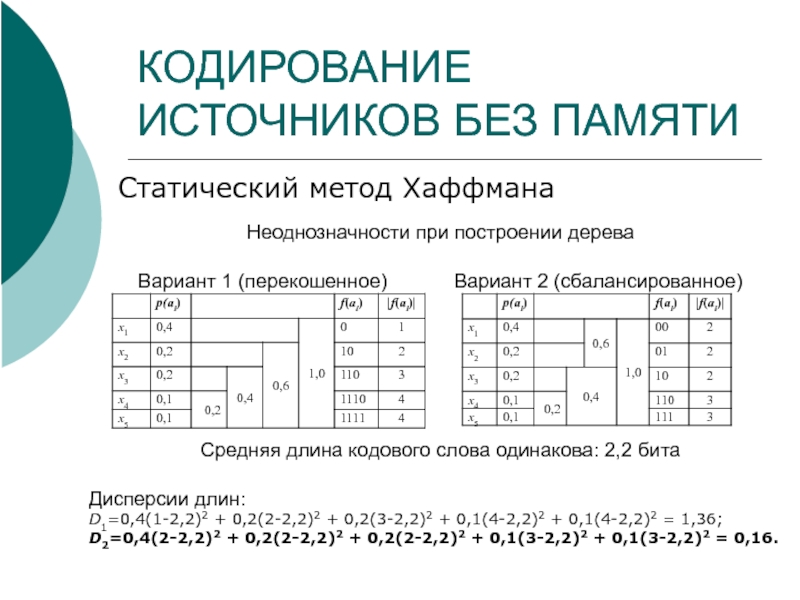
Слайд 14КОДИРОВАНИЕ ИСТОЧНИКОВ БЕЗ ПАМЯТИ
Статический метод Хаффмана
Неоднозначности при построении дерева
Вариант 1 (перекошенное)
Средняя длина кодового слова одинакова: 2,2 бита
Дисперсии длин:
D1=0,4(1-2,2)2 + 0,2(2-2,2)2 + 0,2(3-2,2)2 + 0,1(4-2,2)2 + 0,1(4-2,2)2 = 1,36;
D2=0,4(2-2,2)2 + 0,2(2-2,2)2 + 0,2(2-2,2)2 + 0,1(3-2,2)2 + 0,1(3-2,2)2 = 0,16.
Слайд 15КОДИРОВАНИЕ ИСТОЧНИКОВ БЕЗ ПАМЯТИ
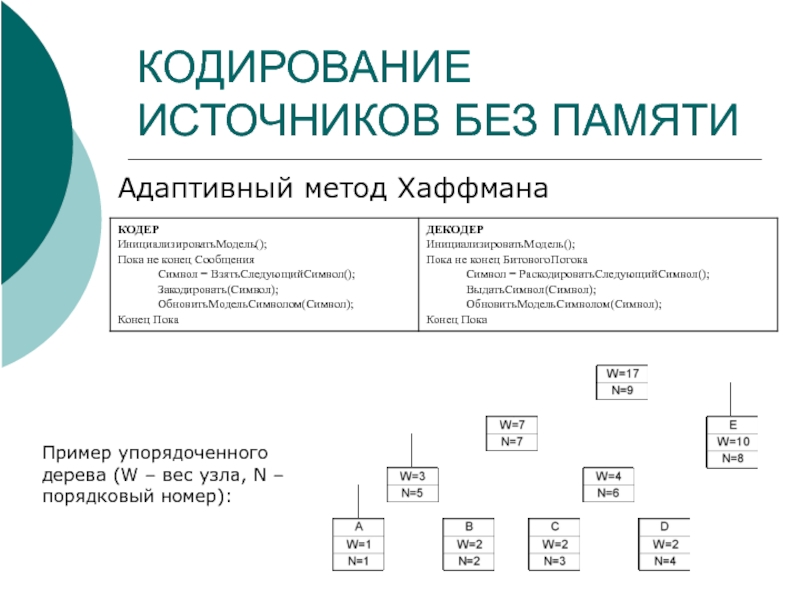
Адаптивный метод Хаффмана
Пример упорядоченного дерева (W – вес
Слайд 16КОДИРОВАНИЕ ИСТОЧНИКОВ БЕЗ ПАМЯТИ
Адаптивный метод Хаффмана
Обновление дерева выполняется в 2 этапа:
1-й
После кодирования символа "А"
Слайд 17КОДИРОВАНИЕ ИСТОЧНИКОВ БЕЗ ПАМЯТИ
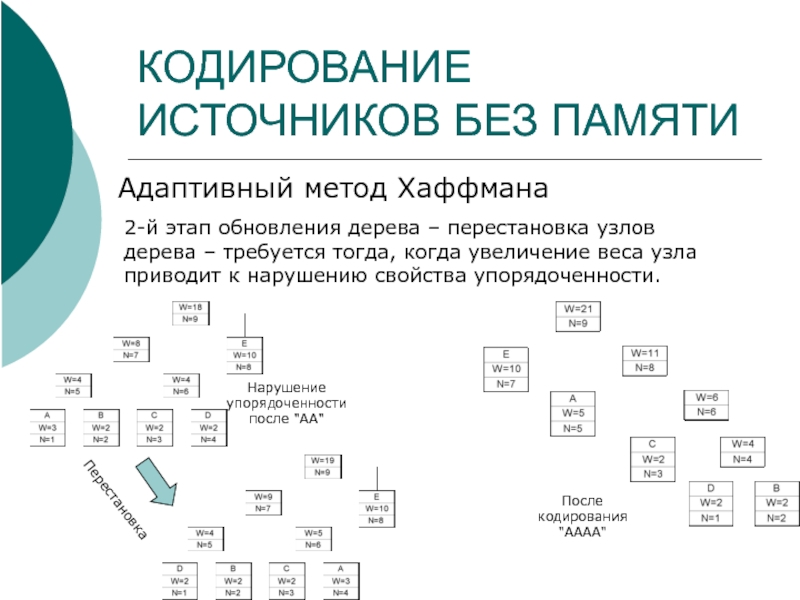
Адаптивный метод Хаффмана
2-й этап обновления дерева – перестановка
Перестановка
Нарушение упорядоченности после "АА"
После кодирования "АААА"
Слайд 18КОДИРОВАНИЕ ИСТОЧНИКОВ БЕЗ ПАМЯТИ
Адаптивный метод Хаффмана
Проблемы адаптивного кодирования:
- инициализация модели (специальные
- переполнение.
Метод расширяющегося префикса (splay trees)
Класс алгоритмов расширяющегося префикса (расширяющихся деревьев – splay trees), в которых деревья, используемые при сжатии данных, могут не иметь постоянной упорядоченности.
Это существенно упрощает процедуры обработки дерева и позволяет повысить быстродействие алгоритма при незначительной потере эффективности кодирования.
Слайд 19КОДИРОВАНИЕ ИСТОЧНИКОВ БЕЗ ПАМЯТИ
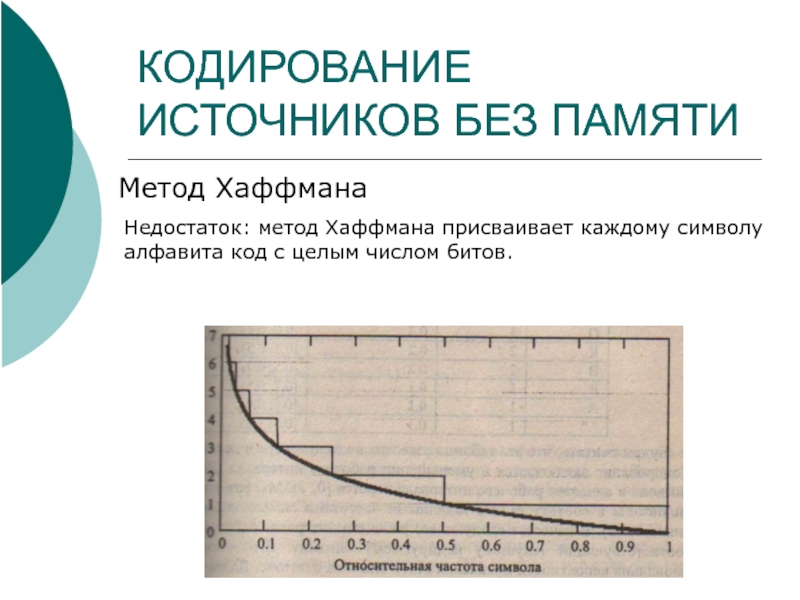
Метод Хаффмана
Недостаток: метод Хаффмана присваивает каждому символу алфавита
Слайд 20КОДИРОВАНИЕ ИСТОЧНИКОВ БЕЗ ПАМЯТИ
Арифметическое кодирование
Формирование одного (длинного) кода для всего потока
Сообщение: ДЛИННОШЕЕЕ
Слайд 21КОДИРОВАНИЕ ИСТОЧНИКОВ БЕЗ ПАМЯТИ
Арифметическое кодирование
Кодер
НижняяГраница = 0.0;
ВерхняяГраница = 1.0;
ПОКА ((ОчереднойСимвол=ВзятьОчереднойСимвол()) !=
Интервал = ВерхняяГраница – НижняяГраница;
НижняяГраница = НижняяГраница + Интервал * НижняяГраницаИнтервала(ОчереднойСимвол);
ВерхняяГраница = НижняяГраница + Интервал * ВерхняяГраницаИнтервала(ОчереднойСимвол);
КОНЕЦ ПОКА;
Выдать(НижняяГраница);
Слайд 22КОДИРОВАНИЕ ИСТОЧНИКОВ БЕЗ ПАМЯТИ
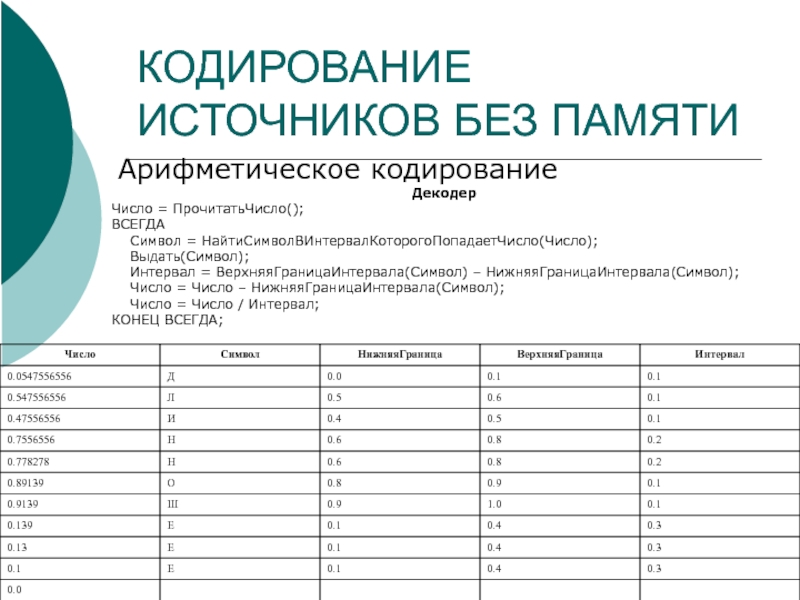
Арифметическое кодирование
Декодер
Число = ПрочитатьЧисло();
ВСЕГДА
Символ = НайтиСимволВИнтервалКоторогоПопадаетЧисло(Число);
Интервал = ВерхняяГраницаИнтервала(Символ) – НижняяГраницаИнтервала(Символ);
Число = Число – НижняяГраницаИнтервала(Символ);
Число = Число / Интервал;
КОНЕЦ ВСЕГДА;
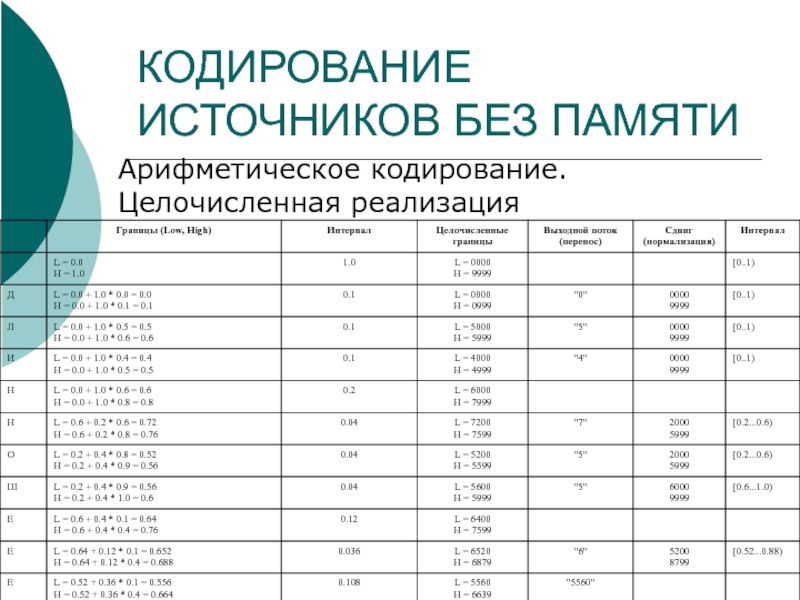
Слайд 24КОДИРОВАНИЕ ИСТОЧНИКОВ БЕЗ ПАМЯТИ
Low0 = 0; High0 = 65535;
i =
delitel = b[clast]; // delitel = 10
FIRST_QTR = (High0+1) / 4; // 16384 = 010000000..
HALF = FIRST_QTR * 2; // 32768 = 100000000..
THIRD_QTR = FIRST_QTR * 3; // 49152 = 110000000..
cntr = 0;
while not eof()
{
c = ReadSymbol(); // Взять входной символ
j = IndexForSymbol(c); // Индекс по таблице
i++;
Interval = Highi-1 – Lowi-1 + 1; // Текущий интервал
Lowi = Lowi-1 + b[j-1]*Interval / delitel; // Нижняя граница
Highi = Lowi-1 + b[j]*Interval / delitel - 1; // Верхняя граница
for ( ; ; ) // Обрабатываем варианты
{
if (Highi < HALF) // у обоих границ старший бит = 0
OutputBitPlusFollow(0);
else if (Lowi > HALF) // у обоих границ старший бит = 1
{
OutputBitPlusFollow(1);
Lowi -= HALF; // обнуляем старший бит
Highi -= HALF;
}
else if ((Lowi >= FIRST_QTR) && (Highi <=THIRD_QTR)) // сближаются!
{
cntr ++; // наращиваем счетчик
Lowi -= FIRST_QTR; // расширяем интервал
Highi -= FIRST_QTR;
}
else // диапазон еще достаточно широк
break;
Lowi = 2 * Lowi;
Highi = 2 * Highi + 1;
}
}
void OutputBitPlusFollow(int bit)
{
WriteStreamBit(bit);
for (; cntr>0; cntr--)
WriteStreamBit(!bit);
}
Арифметическое кодирование. Кодер
Слайд 25КОДИРОВАНИЕ ИСТОЧНИКОВ БЕЗ ПАМЯТИ
Арифметическое кодирование. Декодер
Low0 = 0; High0 = 65535;
i = 0;
delitel = b[clast]; // delitel = 10
FIRST_QTR = (High0+1) / 4; // 16384 = 010000000..
HALF = FIRST_QTR * 2; // 32768 = 100000000..
THIRD_QTR = FIRST_QTR * 3; // 49152 = 110000000..
Value = Read16Bit(); // Чтение из потока первого слова
Interval = Highi-1 – Lowi-1 + 1; // Текущий интервал
Cum = (Value – Lowi + 1) * delitel – 1) / Interval; // Накопленная сумма
for (j=1; b[j]
// Пересчитать границы
Lowi = Lowi-1 + b[j-1]*Interval / delitel; // Нижняя граница
Highi = Lowi-1 + b[j]*Interval / delitel - 1; // Верхняя граница
// Удаление символа из входного потока
for ( ; ; )
{
if (Highi < HALF) // старший бит = 0 – ничего не делать
{
}
else if (Lowi >= HALF)
{
Value -= HALF; // обнуляем старший бит
Lowi -= HALF;
Highi -= HALF;
}
else if ((Lowi >= FIRST_QTR) && (Highi <=THIRD_QTR)) // сближаются!
{
Value -= FIRST_QTR; // обнуляем второй слева бит
Lowi -= FIRST_QTR;
Highi -= FIRST_QTR;
}
else // диапазон еще достаточно широк
break;
Lowi = 2 * Lowi;
Highi = 2 * Highi + 1;
Value = 2 * Value + ReadNextBit(); // Читаем следующий бит из потока
}
Слайд 26КОДИРОВАНИЕ ИСТОЧНИКОВ БЕЗ ПАМЯТИ
Integer Coding (целочисленное кодирование, SEM-кодирование с разделение экспонент
Основная идея - отдельно описывать порядок значения элемента (экспоненту) и отдельно – значащие цифры значения (мантиссу).
Цель – закодировать число произвольной величины, когда верхняя граница чисел потока источника (которую необходимо знать, чтобы выбрать фиксированное количество битов на число) заранее неизвестна.
Примеры (монотонных) кодов: код Левенштейна (1968), Райса (1979), Голомба (1966), Фибоначчи (1939), серия кодов Элайеса (1975).
Слайд 27КОДИРОВАНИЕ ИСТОЧНИКОВ БЕЗ ПАМЯТИ
Integer Coding
Унарный код неотрицательного целого числа n состоит
Монотонный код представляет собой префиксно-свободный код с минимальными длинами кодовых слов, в котором если X1>X2, то длина кодового слова S(X1)≥S(X2) для любых X1, X2, принадлежащих алфавиту источника, т.е. малые значения получают более короткие кодовые слова, чем большие значения.
Слайд 28КОДИРОВАНИЕ ИСТОЧНИКОВ БЕЗ ПАМЯТИ
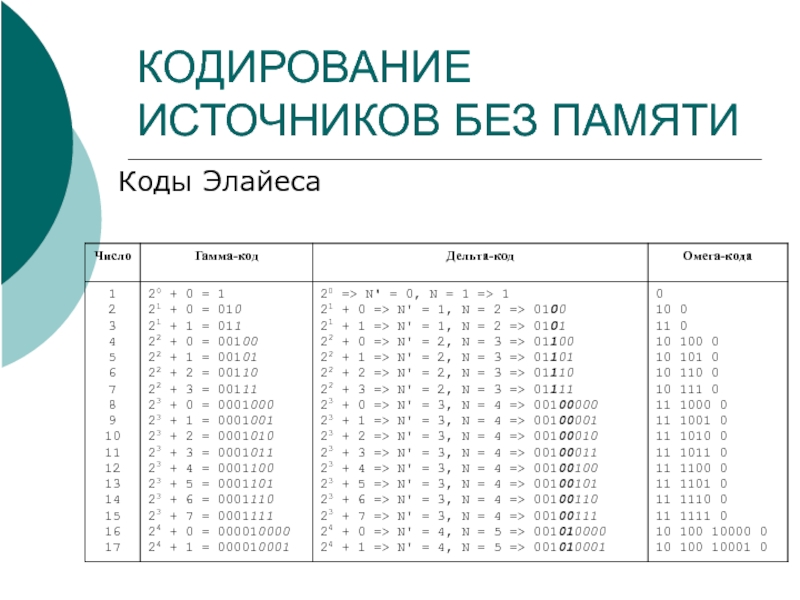
Коды Элайеса
Гамма-код Элайеса числа n представляет собой комбинацию
Дельта-кодами Элайеса называются гамма-коды, в которых унарная часть также закодирована гамма-кодами.
Омега-коды Элайеса рекурсивно кодируют свой префикс, поэтому иногда называются рекурсивными кодами Элайеса.
Слайд 30КОДИРОВАНИЕ ИСТОЧНИКОВ БЕЗ ПАМЯТИ
Еще один вариант кода Элайеса...
elias(i) = ( unar
где bin'(i) – двоичная запись натурального числа i без первой единицы. Унарный код unar(i) сопоставляет числу i двоичную комбинацию виде 1i-10 (например, unar(1) = 0, unar(2) = 10, unar(3) = 110 и т.д.).
Слайд 31КОДИРОВАНИЕ ИСТОЧНИКОВ БЕЗ ПАМЯТИ
Код Левенштейна
Код Левенштейна для числа n получается путем
Декодирования числа заканчивается, как только на месте флагового бита встречается "1" – это и будет последний информационный бит числа (в его реверсивной записи).
Например: 13 = 1101 => 1011 => 0100011. Подчеркнуты флаговые биты, выделены информационные биты.
Слайд 32КОДИРОВАНИЕ ИСТОЧНИКОВ С ПАМЯТЬЮ
Кодирование длин серий (RLE)
Предположим, что для представления длины
В соответствии с алгоритмом кодирования, это можно сделать только в том случае, если длина серии находится между 0 и 2k-2. Приемник генерирует указанное число нулей и затем одну 1.
Если получено число 0, то приемник просто генерирует 1.
Если послано число 2k-1, приемник генерирует 2k-1 нулей, за которыми не следует 1. Если после этого послано 0, то генерируется 1; для любого другого числа генерируется указанное число нулей и затем единица (если это не снова 2k-1).
Таким образом, передав достаточное число k-значных двоичных чисел, можно указать любую длину серии, состоящей из нулей.
Слайд 33КОДИРОВАНИЕ ИСТОЧНИКОВ С ПАМЯТЬЮ
Словарное сжатие
Входной алфавит A={0,1,...,|A|-1}.
x – слово, xji
Разобьем слово x последовательно на несовпадающие подслова (парсинг):
таким образом, что все слова, за исключением, возможно, последнего, различны и для каждого j=1,2,...,p+1 при nj-nj-1>1 существует i, i
Конкатенация кодов всех слов образует слово f(x), для длины которого имеем
С учетом того, что максимальное число C(x) слов, на которые разбивается x, может лишь превзойти p (C(x)≥p), имеем
Слайд 34КОДИРОВАНИЕ ИСТОЧНИКОВ С ПАМЯТЬЮ
Алгоритм LZ77
В качестве модели данных используется "скользящее" по
Алгоритм LZ77 выдает коды, состоящие из трех элементов:
- смещение в словаре относительно начала буфера, совпадающей с содержимым буфера (i);
- длина подстроки (j);
- первый символ в буфере, следующий за подстрокой (s).
Дополнительные соглашения:
- нулевое смещение зарезервировано для обозначения конца кодирования;
- последний символ словаря соответствует единичному смещению относительно символа начала буфера;
- если имеется несколько фраз с одинаковой длиной, то выбирается ближайшая к буферу;
- в неопределенных ситуациях – когда длина совпадения нулевая – смещению (для определенности) присваивается, например, единичное значение.
Слайд 35КОДИРОВАНИЕ ИСТОЧНИКОВ С ПАМЯТЬЮ
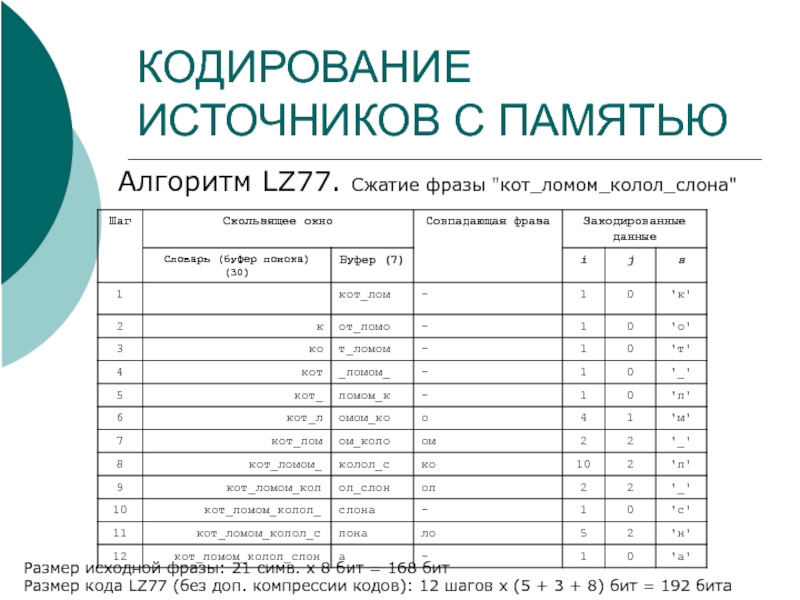
Алгоритм LZ77. Сжатие фразы "кот_ломом_колол_слона"
Размер исходной фразы: 21
Размер кода LZ77 (без доп. компрессии кодов): 12 шагов х (5 + 3 + 8) бит = 192 бита
Слайд 36КОДИРОВАНИЕ ИСТОЧНИКОВ С ПАМЯТЬЮ
Алгоритм LZSS
Основная идея алгоритма заключается в добавлении к
- записывать символы в явном виде, когда соответствующий им код имеет большую длину, и, следовательно, словарное кодирование только вредит;
- обрабатывать ни разу не встреченные до текущего момента символы.
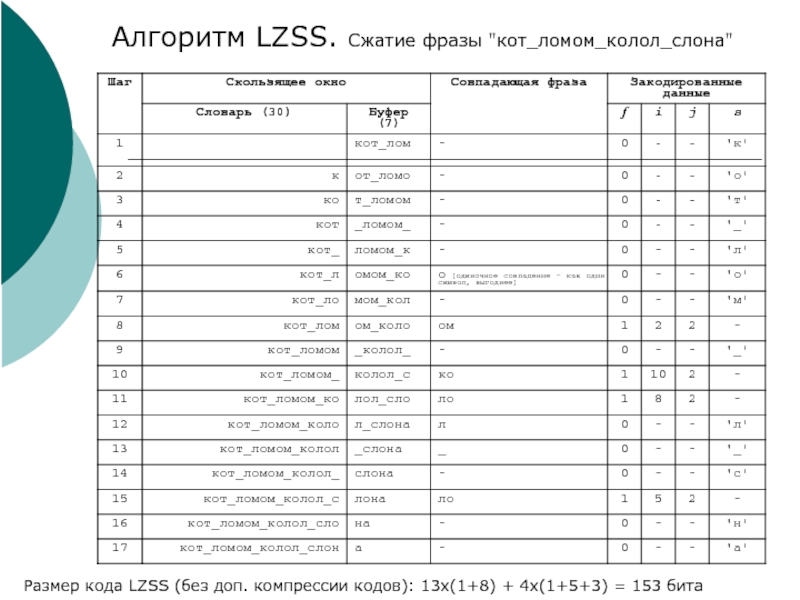
Слайд 37Алгоритм LZSS. Сжатие фразы "кот_ломом_колол_слона"
Размер кода LZSS (без доп. компрессии кодов):
Слайд 38КОДИРОВАНИЕ ИСТОЧНИКОВ С ПАМЯТЬЮ
Алгоритм LZ78
На каждом шаге в словарь вставляется новая
В словаре не может быть совпадающих фраз.
Кодер порождает только последовательность кодов фраз. Каждый код состоит из номера (индекса) n "родительской" фразы S или префикса, и символа s. В начале обработки словарь пуст.
Дополнительные соглашения:
- фраза с номером 0 обозначает конец сжатой строки;
- фраза с номером 1 задает пустую фразу словаря.
Слайд 39КОДИРОВАНИЕ ИСТОЧНИКОВ С ПАМЯТЬЮ
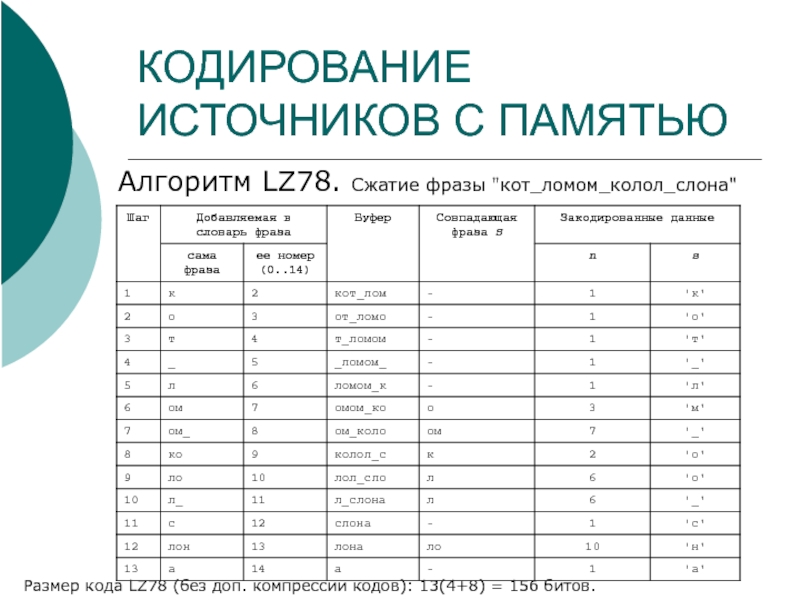
Алгоритм LZ78. Сжатие фразы "кот_ломом_колол_слона"
Размер кода LZ78 (без
Слайд 40ПРЕОБРАЗОВАНИЕ БЛОКОВ ДАННЫХ
Преобразование Барроуза-Уиллера (BWT)
Цель обработки – преобразовать входной блок (последовательность
Вариант схемы кодирования (последовательное применение алгоритмов):
- преобразование BWT;
- преобразование MTF;
- статистический кодер для сжатия данных, полученных в результате последовательного применения двух предыдущих преобразований.
Алгоритм BWT оперирует сразу всем сообщением или значительным по объему блоком данных, что осложняет его применения в системах поточного кодирования данных (системах реального времени).
Слайд 41ПРЕОБРАЗОВАНИЕ БЛОКОВ ДАННЫХ
Преобразование Барроуза-Уиллера (BWT)
Процедура преобразования выполняется следующим образом:
- выделяется блок
- формируется матрица всех перестановок, полученных в результате циклического сдвига блока;
- все перестановки сортируются в соответствии с лексикографическим порядком символов каждой перестановки;
- на выход подается последний столбец матрицы и номер строки, соответствующей оригинальному блоку.
Слайд 44ПРЕОБРАЗОВАНИЕ БЛОКОВ ДАННЫХ
Преобразование Барроуза-Уиллера (BWT)
Важно, что при добавлении любого столбца перемещения
Чтобы получить вектор обратного преобразования следует определить порядок получения символов первого столбца из символов последнего, т.е. отсортировать матрицу по номерам новых строк:
Полученные значения номеров строк T = {2,5,6,7,8,9,10,1,3,0,4} – и есть искомый вектор, содержащий номера позиций символов в строке, которую надо декодировать.
Слайд 45МЕТОДЫ АНАЛИЗА (СРАВНЕНИЯ) АЛГОРИТМОВ КОМПРЕССИИ
Наборы тестовых данных
Принято измерять эффективности компрессоров с
- набор Calgary Compression Corpus (CalgCC) из 14 файлов (+4 дополнительных), большая часть из которых представляет собой тексты на английском языке (художественные, технические, с большим количеством опечаток и т.п.) или языках программирования (программы на С, Лисп, Pascal). Имеются также геофизические данные, объектные файлы, факсимильные изображения;
- Canterbury Compression Corpus (CantCC) – предложен той же группой исследователей, что и CalgCC и является альтернативой морально устаревшему CalgCC (с точки зрения типов обрабатываемых данных);
- наборы файлов из Archive Comparison Test (ACT) – текстовые файлы, исполняемые файлы, звуковые файлы, полноцветные изображения;
- наборы файлов из тестов Art Of Lossless Data Compression (ARTest) – полноцветные изображения, текстовые файлы, разнородные файлы;
- файлы из Compression Comparison Вадима Юткина (VYCCT) – 8 файлов разных типов.














![КОДИРОВАНИЕ ИСТОЧНИКОВ БЕЗ ПАМЯТИLow0 = 0; High0 = 65535; i = 0;delitel = b[clast]; //](/img/tmb/3/249511/c502f12fdfc5a55820a8567421d53a26-800x.jpg)