- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Динамическое программирование презентация
Содержание
- 1. Динамическое программирование
- 7. Числа Фибоначчи Решение методом «динамического программирования» предполагает
- 8. Задача об n – битных двоичных числах
- 9. F[N] = F[N-1] + F[N-2], при N
- 10. Зайчик на лесенке На вершине лесенки,
- 11. Зайчик на лесенке Пусть зайчик находится
- 12. Программа на С++ #include using namespace
- 13. Задача о фишке Фишка может двигаться по
- 14. Задача о фишке Пусть S[i] - количество
- 15. Алгоритм динамического программирования Динамическое программирование – метод
- 16. Задача о черепашке Сколько вариантов пройти с левого нижнего угла в правый верхний угол?
- 17. Формулировка задачи динамического программирования Дано: множество
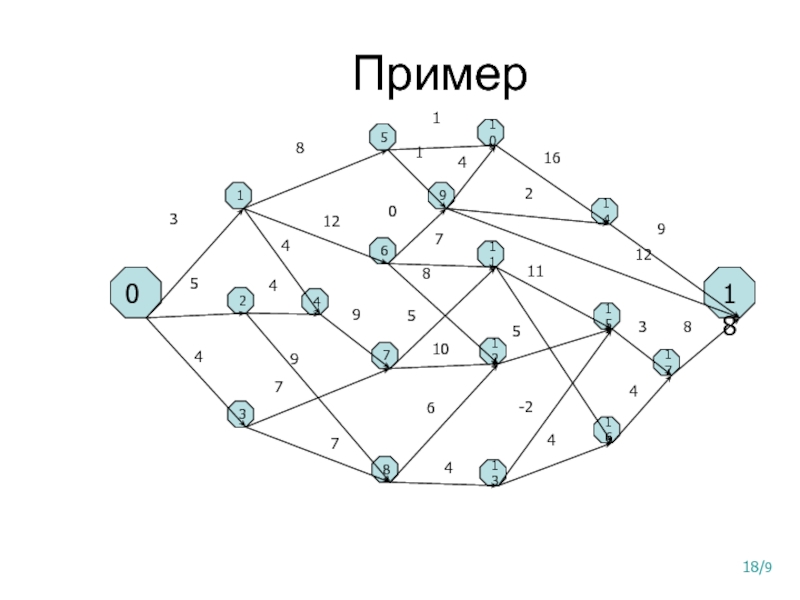
- 18. Пример 0 18 1 2 3
- 19. Математическая запись /9
- 20. Принцип оптимальности Беллмана Если вершины A
- 21. Алгоритм решения задач динамического программирования 0
- 22. Алгоритм решения задач динамического программирования 0
- 23. Экономические приложения /9
- 24. Условия применения динамического программирования 1.
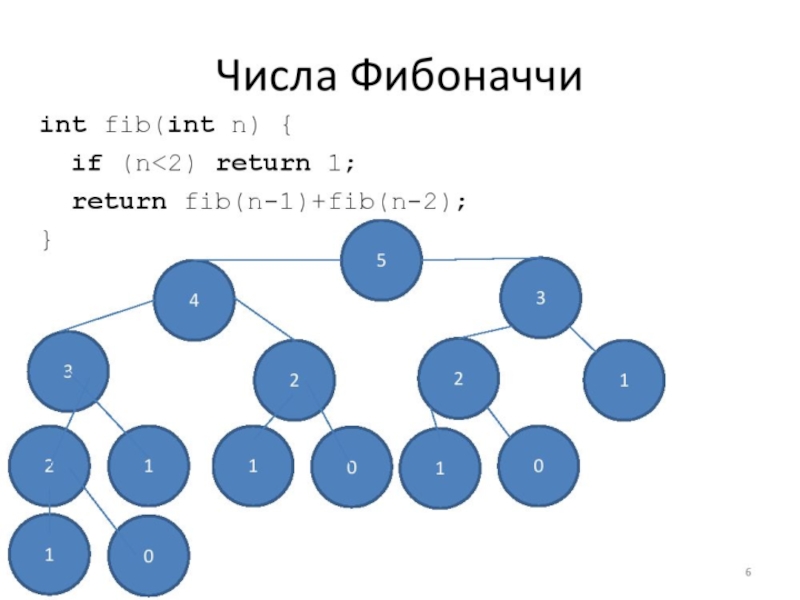
Слайд 7Числа Фибоначчи
Решение методом «динамического программирования» предполагает запоминание каждого числа в массиве.
Тогда
F[N] = F[N-1] + F[N-2], при N > 2.
Слайд 8Задача об n – битных двоичных числах
Найти количество F всех
Слайд 10Зайчик на лесенке
На вершине лесенки, содержащей N ступенек, находится зайчик,
Зайчик может прыгнуть на следующую ступеньку, на ступеньку через 1 или 2.
Определить число всевозможных “маршрутов” зайчика с вершины на землю.
Слайд 11Зайчик на лесенке
Пусть зайчик находится на ступеньке с номером X.
По
Пусть F(X) - число маршрутов со ступеньки X до земли
F[X] = F[X – 1] + F[X – 2] + F[X – 3]
Слайд 12Программа на С++
#include
using namespace std;
int main()
{ int N; long long F[31];
cin>>N;
F[1]=1;F[2]=2;F[3]=4;
for(int i=4; i <= N; i++)
F[i]=F[i-1]+F[i-2]+F[i-3];
cout<
}
Слайд 13Задача о фишке
Фишка может двигаться по полю длины N
только вперед. Длина
более K (N, K ≤10).
Найти количество различных путей, по которым фишка может пройти поле от позиции 1 до позиции N.
Слайд 14Задача о фишке
Пусть S[i] - количество различных путей, по которым фишка
S[i+1]=S[i]+S[i-1]+...+S[i-k]
Вычисляя последовательно значения величин S[1], S[2],..., S[N] по правилу, получаем значение S[N] – решение задачи
Слайд 15Алгоритм динамического программирования
Динамическое программирование – метод оптимизации, приспособленный к задачам, в
Его алгоритм можно сформулировать так:
Выделить и описать подзадачи, через решение которых будет выражаться искомое решение;
Выписать рекуррентные соотношения (уравнения), связывающие оптимальные значения параметра для всех подзадач;
Вычислить оптимальное значение параметра для всех подзадач;
Построить само оптимальное решение.
В задачах на подсчет количеств допустимых вариантов (задачи рассмотрены выше) пункт 4 не нужен
Слайд 17Формулировка задачи динамического программирования
Дано:
множество состояний
в том числе начальное и конечное
множество
с каждым переходом связывается числовой параметр
интерпретируется как затраты, выгода, расстояние, время и т.п.
Найти:
оптимальную последовательность переходов (путь) из начального состояния в конечное
максимум или минимум суммы числовых параметров
предполагается, что хотя бы один путь из начального состояния в конечное существует
/9
Слайд 20Принцип оптимальности Беллмана
Если вершины A и B лежат на оптимальном
Следствие
Чтобы найти оптимальный путь от 0 до A, достаточно исследовать продолжения к A всех оптимальных путей до вершин, предшествующих A
Продолжения неоптимальных путей к предшествующим вершинам можно не просчитывать: они никогда не дадут оптимального пути к A
Принцип Беллмана позволяет построить простую и эффективную вычислительную процедуру для решения задач динамического программирования
/9
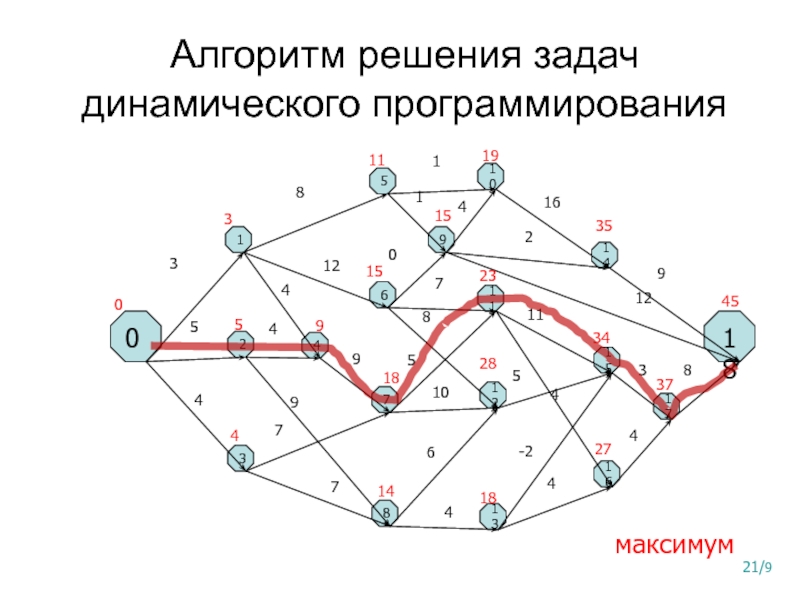
Слайд 21Алгоритм решения задач динамического программирования
0
18
1
2
3
5
7
6
8
10
12
11
13
4
14
15
16
9
17
3
8
5
4
4
7
4
12
7
6
9
1
1
4
2
16
0
7
9
10
8
5
5
11
12
9
3
8
4
-2
4
4
0
3
11
15
15
19
35
5
9
4
18
14
18
28
23
34
4
27
37
45
максимум
/9
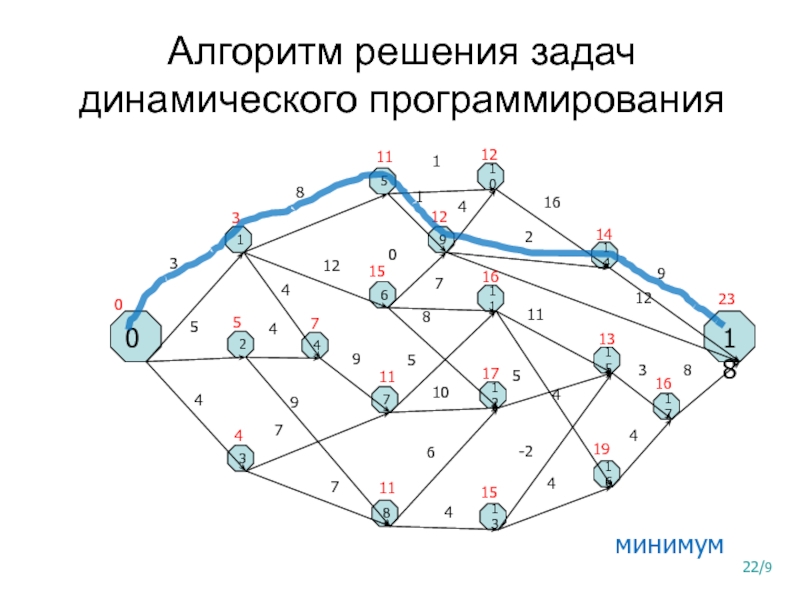
Слайд 22Алгоритм решения задач динамического программирования
0
18
1
2
3
5
7
6
8
10
12
11
13
4
14
15
16
9
17
3
8
5
4
4
7
4
12
7
6
9
1
1
4
2
16
0
7
9
10
8
5
5
11
12
9
3
8
4
-2
4
4
0
4
5
11
3
7
11
15
17
15
16
13
4
19
16
11
12
12
14
23
минимум
/9
Слайд 24Условия применения динамического программирования
1. Оптимальное решение задачи выражается через
2. Небольшое число подзадач, что позволяет хранить решения каждой подзадачи в таблице. Уменьшение числа подзадач происходит из-за многократного их повторения(т.н. перекрывающиеся подзадачи).
3. Дискретность (неделимость) величин, рассматриваемых в задаче.
4. Один из главных критериев, когда принцип ДП дает эффект уменьшения временной сложности: если в процессе решения необходимо многократно перебирать одни и те же варианты (за счет увеличения емкостной сложности уменьшается временная сложность).







![F[N] = F[N-1] + F[N-2], при N > 2. Задача об n – битных двоичных](/img/tmb/4/327238/bde421936ac101eb5874d7ffb049cf31-800x.jpg)


![Программа на С++#include using namespace std;int main(){ int N; long long F[31]; cin>>N; F[1]=1;F[2]=2;F[3]=4; for(int i=4; i](/img/tmb/4/327238/a32c1ad2e6e2c61dc1d07f3b641bd5cf-800x.jpg)

![Задача о фишкеПусть S[i] - количество различных путей, по которым фишка может пройти поле от](/img/tmb/4/327238/497fa9c3d9b874a93f46e20452e17e70-800x.jpg)