- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Деревья. Терминология презентация
Содержание
- 1. Деревья. Терминология
- 2. Структура дерева Корневым деревом называется множество элементов,
- 3. Определения Формальное определение дерева: Один узел является
- 4. Определения Родитель узла n – узел дерева,
- 5. Определения Путем из узла n1 в узел
- 6. Определения
- 7. Определения Высота узла n – длина самого
- 8. Способы отображения деревьев: Вложенные множества A B C
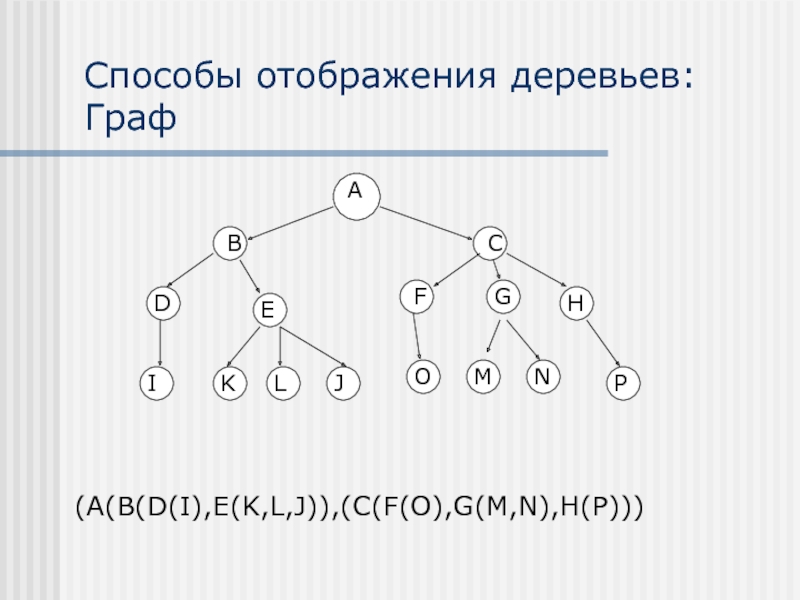
- 9. Способы отображения деревьев: Граф (A(B(D(I),E(K,L,J)),(C(F(O),G(M,N),H(P)))
- 10. Бинарные деревья Бинарным деревом называется множество узлов,
- 11. Бинарное дерево поиска Упорядоченным называется дерево, у
Слайд 2Структура дерева
Корневым деревом называется множество элементов, в котором выделен один, называемый
корнем, а все остальные элементы разбиты на непересекающиеся подмножества, каждое из которых, в свою очередь, есть дерево
Слайд 3Определения
Формальное определение дерева:
Один узел является деревом
Этот же узел является и корнем
этого дерева
Пусть n –узел, а T1 ,T2 ,… ,Tk - деревья с корнями n1, n2,…, nk соответственно. Тогда можно построить новое дерево, сделав n родителем узлов n1, n2,…, nk . В этом дереве n – корень, T1 ,T2 ,… ,Tk - поддеревья, n1, n2,…, nk – сыновья узла n/
Пусть n –узел, а T1 ,T2 ,… ,Tk - деревья с корнями n1, n2,…, nk соответственно. Тогда можно построить новое дерево, сделав n родителем узлов n1, n2,…, nk . В этом дереве n – корень, T1 ,T2 ,… ,Tk - поддеревья, n1, n2,…, nk – сыновья узла n/
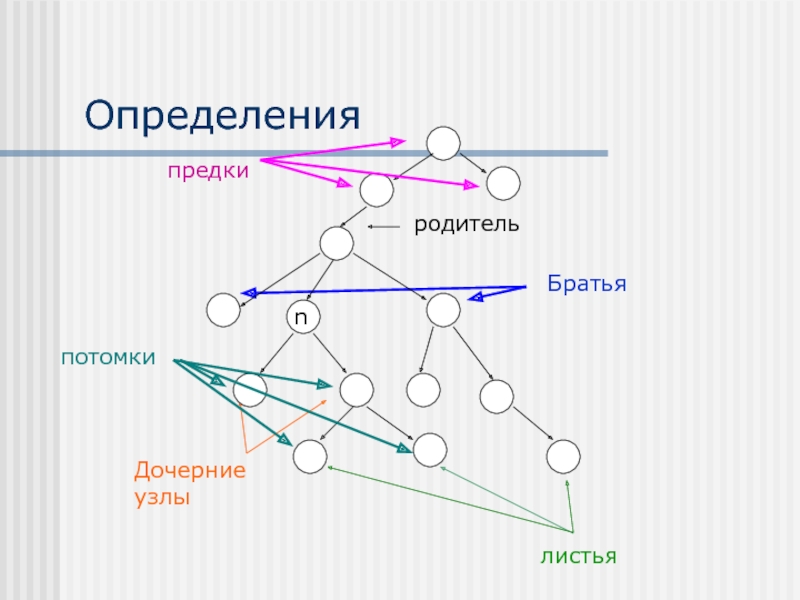
Слайд 4Определения
Родитель узла n – узел дерева, находящийся непосредственно над узлом n
Дочерний
узел узла n –узел дерева, находящийся непосредственно под узлом n
Корень –единственный узел дерева, не имеющий родителей
Лист – узел, не имеющий дочерних узлов
Братья – узлы, имеющие общих родителей
Корень –единственный узел дерева, не имеющий родителей
Лист – узел, не имеющий дочерних узлов
Братья – узлы, имеющие общих родителей
Слайд 5Определения
Путем из узла n1 в узел nk называется последовательность узлов n1,
n2, … nk , где для всех i: 1<=IПредок узла n – узел, расположенный на пути от корня к узлу n
Потомок узла n – расположенный на пути от узла n к листу
Потомок узла n – расположенный на пути от узла n к листу
Слайд 7Определения
Высота узла n – длина самого длинного пути из узла n
до какого-нибудь листа
Высота дерева – высота его корня
Глубина узла n – длина пути от корня до этого узла
Степень узла n – число непосредственных потомков
Высота дерева – высота его корня
Глубина узла n – длина пути от корня до этого узла
Степень узла n – число непосредственных потомков
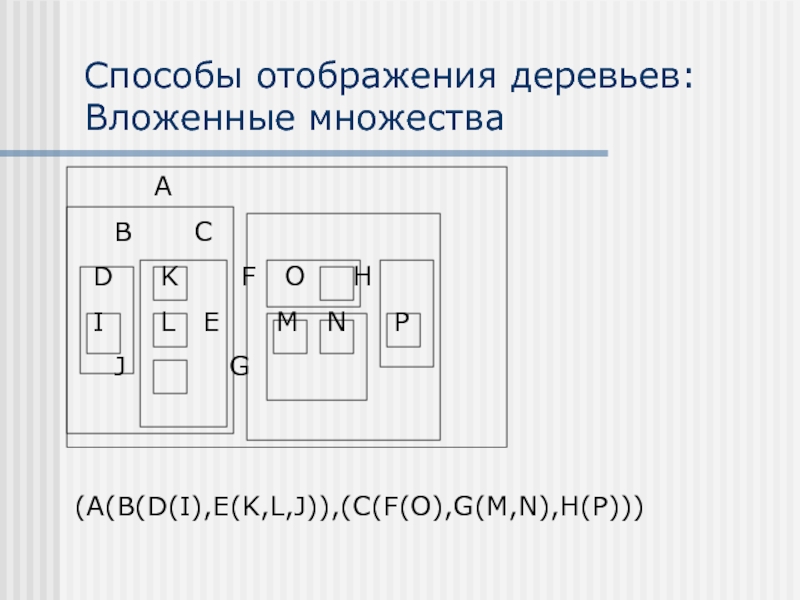
Слайд 8Способы отображения деревьев:
Вложенные множества
A
B C
D K
F O H
I L E M N P
J G
I L E M N P
J G
(A(B(D(I),E(K,L,J)),(C(F(O),G(M,N),H(P)))
Слайд 10Бинарные деревья
Бинарным деревом называется множество узлов, которое либо пусто либо разделено
на корень и два подмножества, которые также представляют собой бинарные деревья
В бинарном дереве каждый узел
Либо пуст
Либо не имеет сыновей
Либо имеет только левого сына
Либо имеет только правого сына
Либо имеет двух сыновей
В бинарном дереве каждый узел
Либо пуст
Либо не имеет сыновей
Либо имеет только левого сына
Либо имеет только правого сына
Либо имеет двух сыновей
Слайд 11Бинарное дерево поиска
Упорядоченным называется дерево, у которого непосредственные потомки каждого узла
упорядочены
Справедливо правило:
Если a и b являются сыновьями одного узла и узел a лежит слева от узла b, то все потомки узла a будут находиться слева от любых потомков узла b
Бинарное дерево, в котором значение каждого узла n больше значения каждого узла левого поддерева, но меньше значения каждого узла правого поддерева, называется бинарным деревом поиска
Справедливо правило:
Если a и b являются сыновьями одного узла и узел a лежит слева от узла b, то все потомки узла a будут находиться слева от любых потомков узла b
Бинарное дерево, в котором значение каждого узла n больше значения каждого узла левого поддерева, но меньше значения каждого узла правого поддерева, называется бинарным деревом поиска