- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
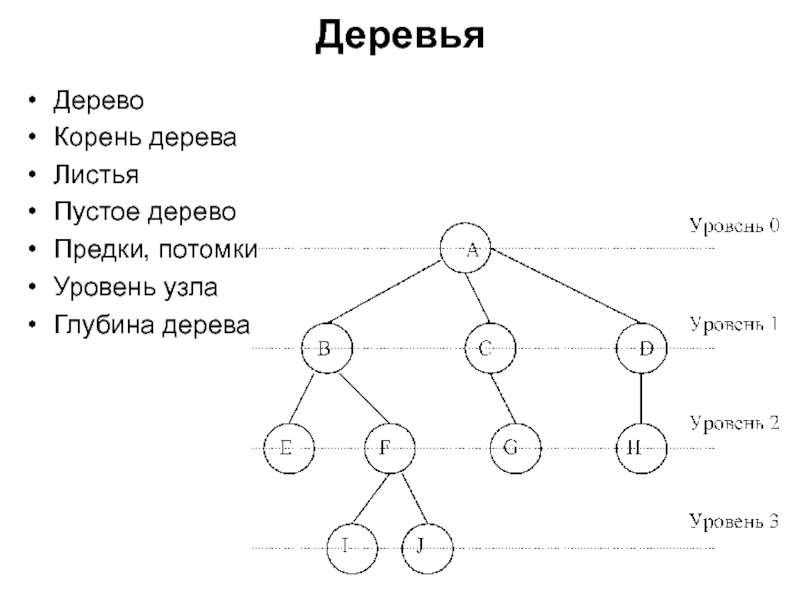
Деревья. Двоичные (бинарные) деревья презентация
Содержание
- 1. Деревья. Двоичные (бинарные) деревья
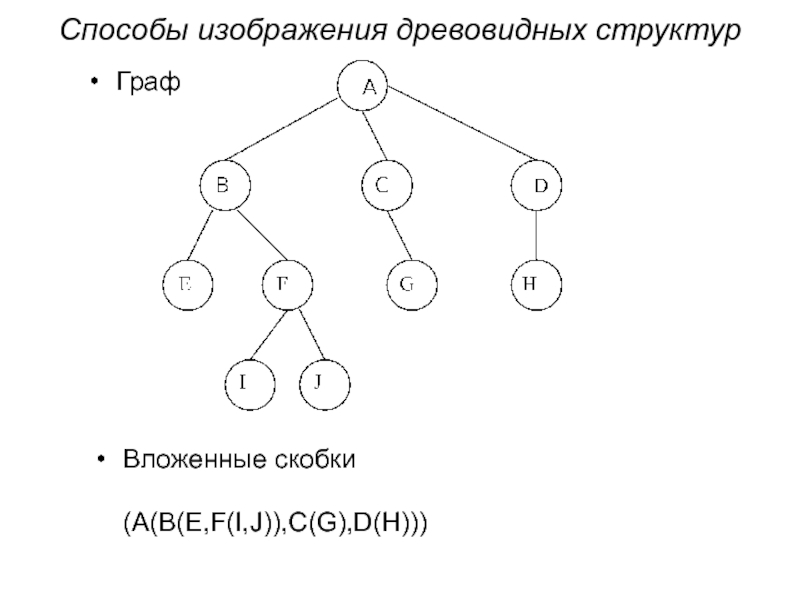
- 2. Способы изображения древовидных структур Граф Вложенные скобки (A(B(E,F(I,J)),C(G),D(H)))
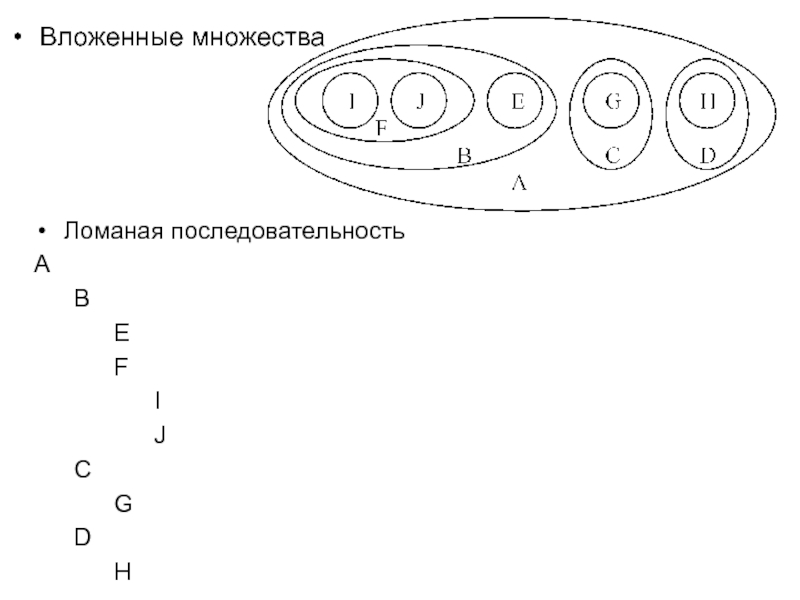
- 3. Вложенные множества Ломаная последовательность A B E F I J C G D H
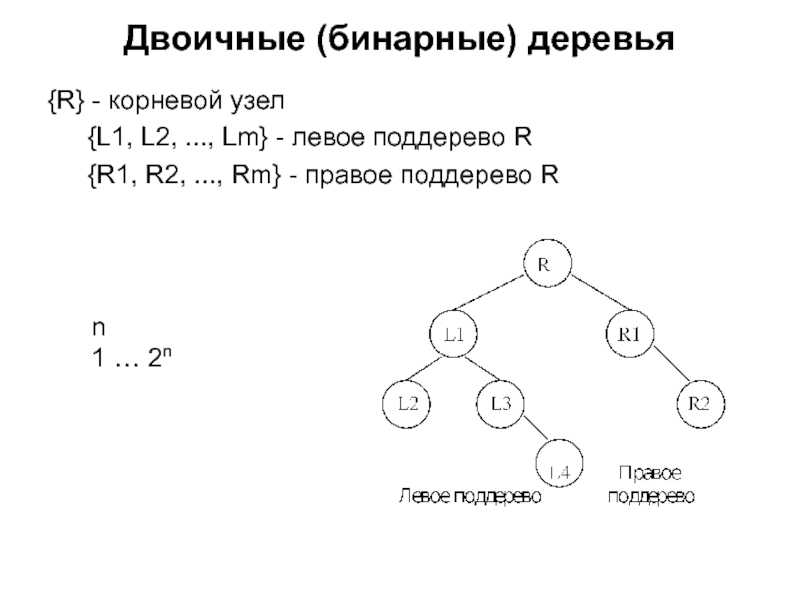
- 4. Двоичные (бинарные) деревья {R} - корневой узел
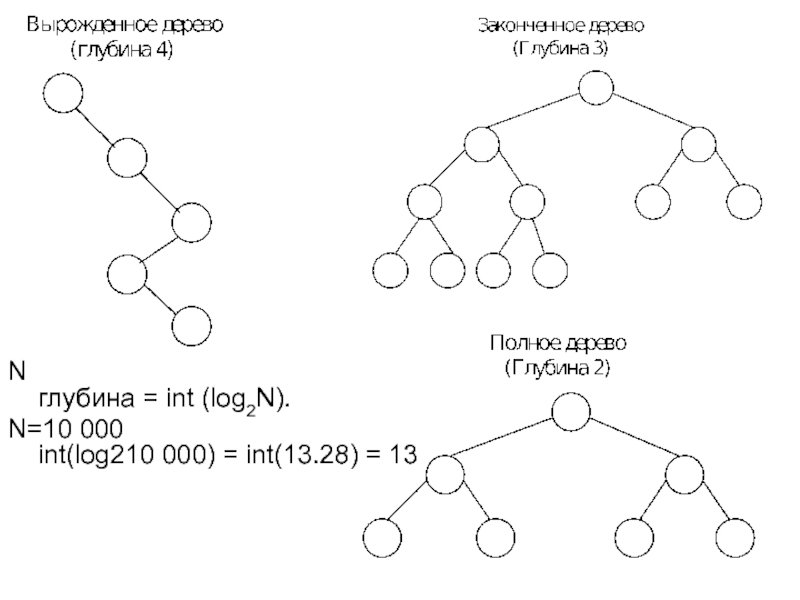
- 5. N глубина = int (log2N). N=10 000 int(log210 000) = int(13.28) = 13
- 6. Структура двоичного дерева С использованием массива TREE[n];
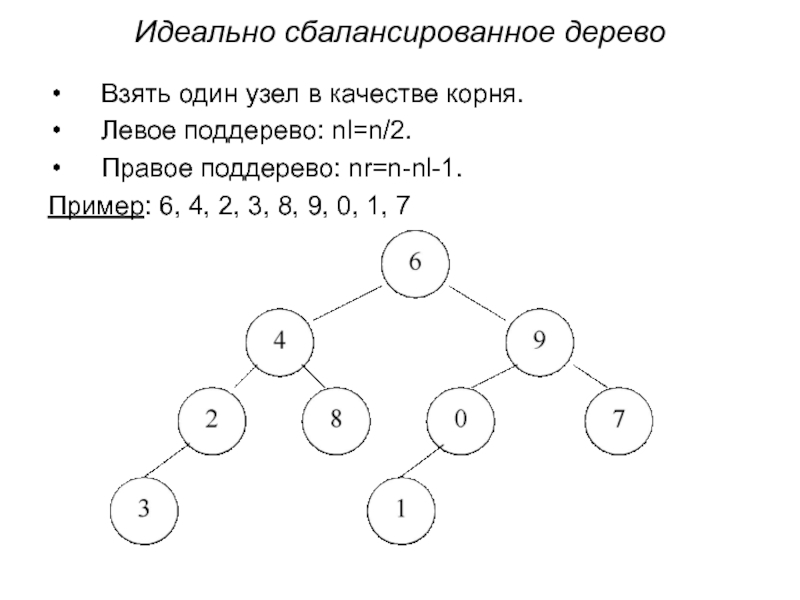
- 7. Идеально сбалансированное дерево Взять один узел в
- 8. TREE* maketree(int n) {TREE *ptr; int nl,
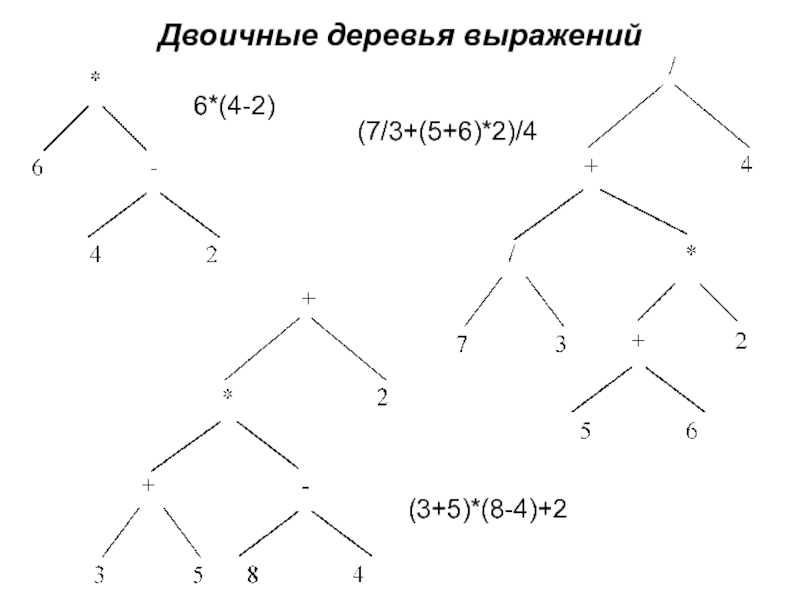
- 9. Двоичные деревья выражений 6*(4-2) (3+5)*(8-4)+2 (7/3+(5+6)*2)/4
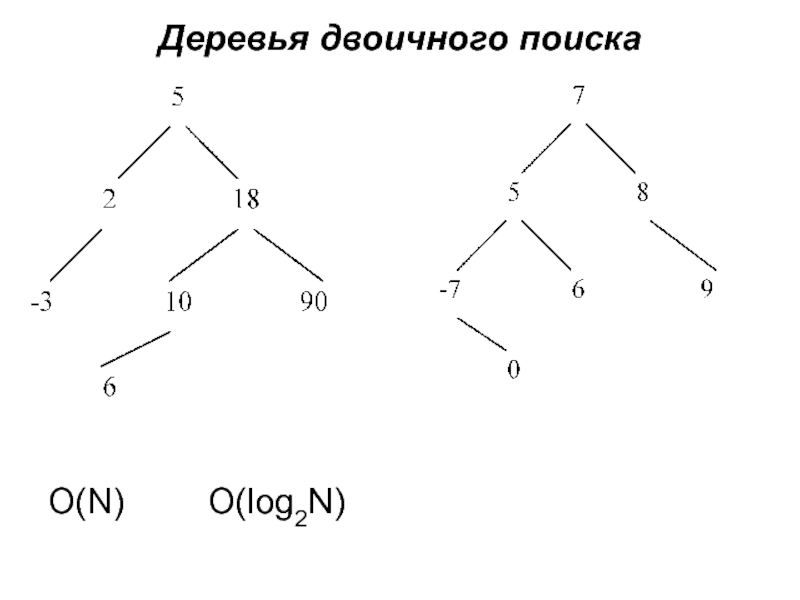
- 10. Деревья двоичного поиска O(N) O(log2N)
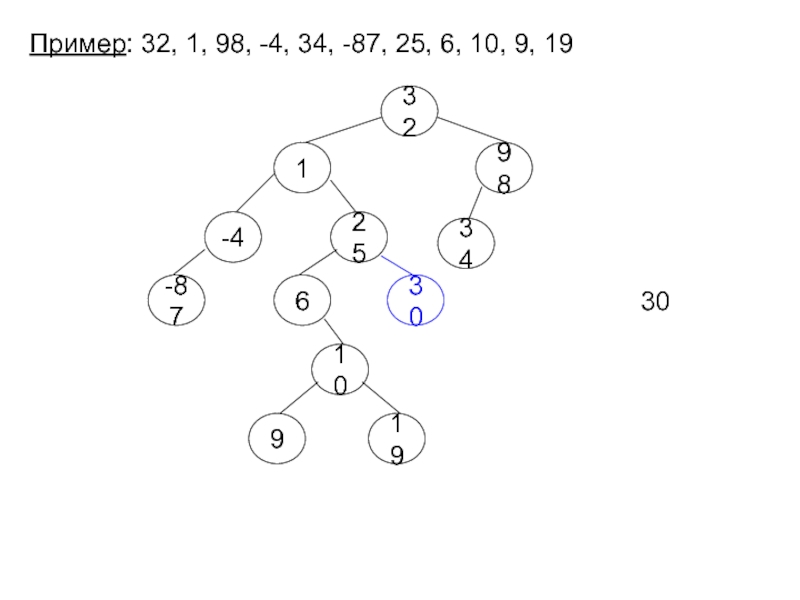
- 11. Пример: 32, 1, 98, -4, 34, -87,
- 12. void build(TREE *tt, char ch) { if
- 13. Операции с двоичными деревьями Алгоритмы поиска TREE
- 14. TREE *parent=NULL; TREE *find(char x, TREE* ptr)
- 15. Алгоритмы обхода дерева Прямой void preorder(TREE *ptr)
- 16. Симметричный void inorder(TREE *ptr) { if (ptr)
- 17. Обратный void postorder(TREE *ptr) { if (ptr)
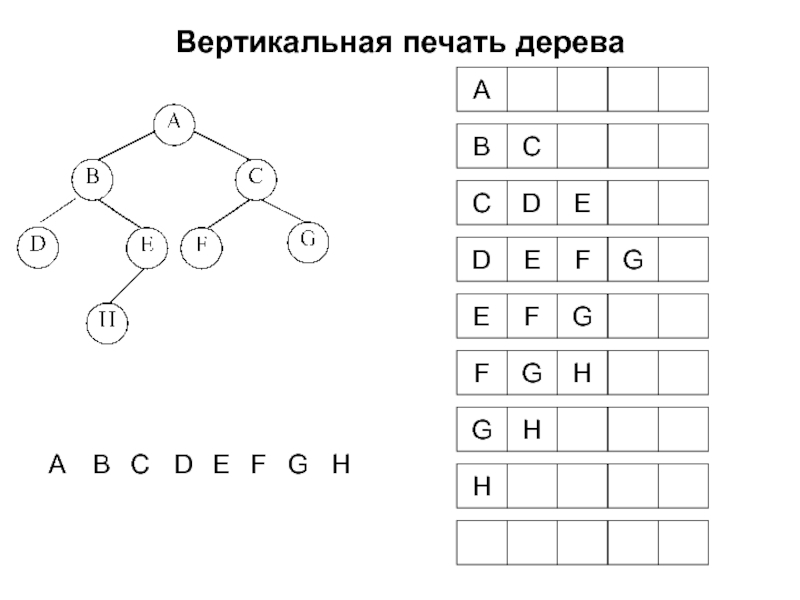
- 18. Вертикальная печать дерева A B C D E F G H
- 19. Удаление дерева TREE* del(TREE *t) { if
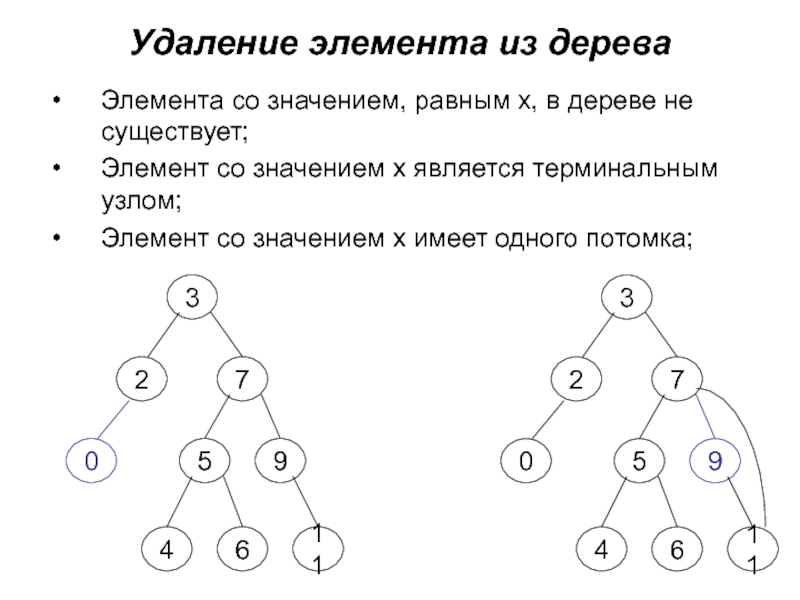
- 20. Удаление элемента из дерева Элемента со значением,
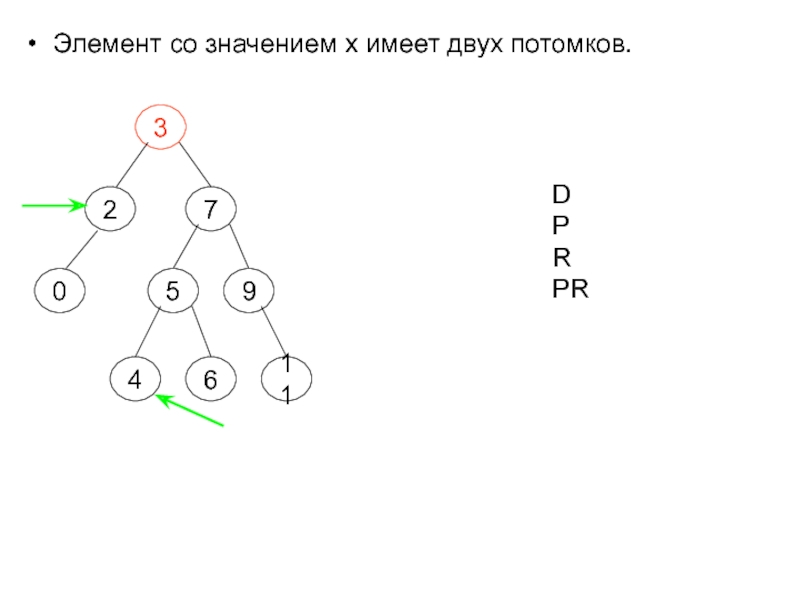
- 21. Элемент со значением х имеет двух потомков.
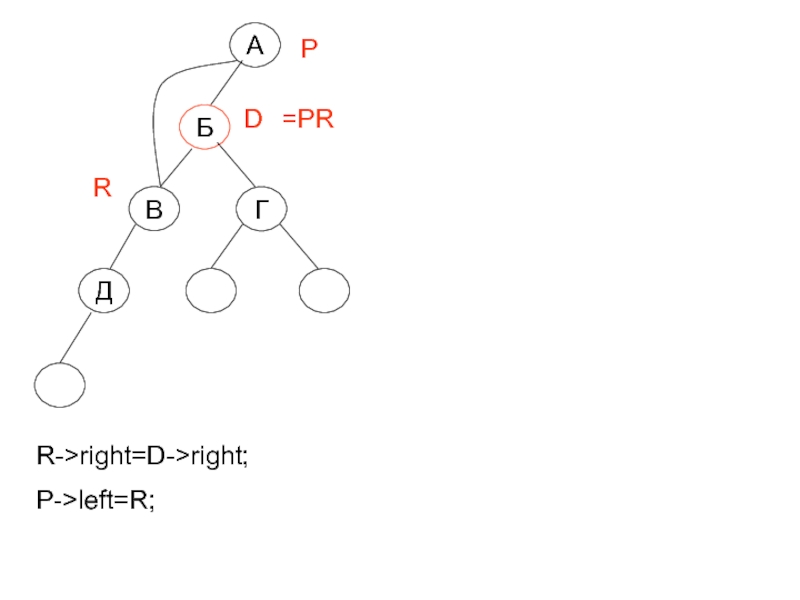
- 22. R->right=D->right; P->left=R; A Б Г
- 23. PR->right=R->left; A Б Г В Д
- 24. Двоичные деревья, представляемые массивами A[i] Индекс
- 25. int A[]={5, 1, 3, 9, 6, 4, #, 7, #, #, #, 2};
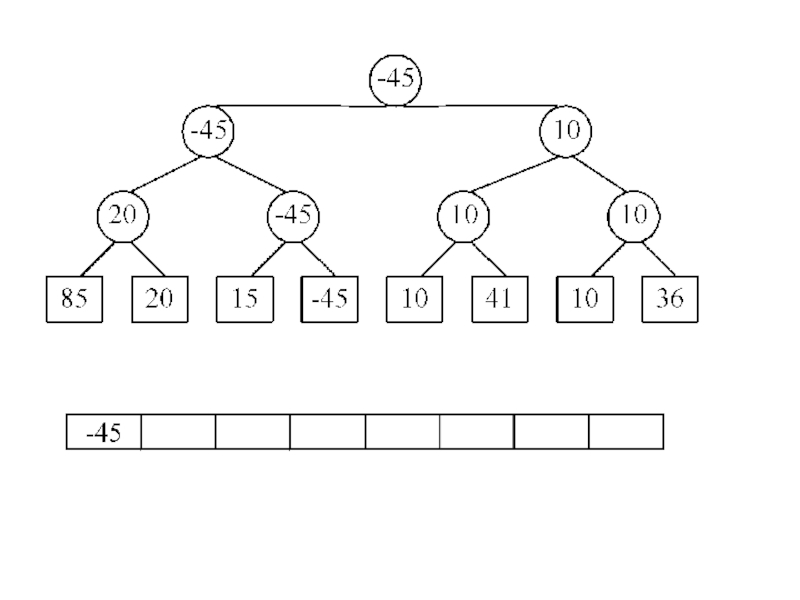
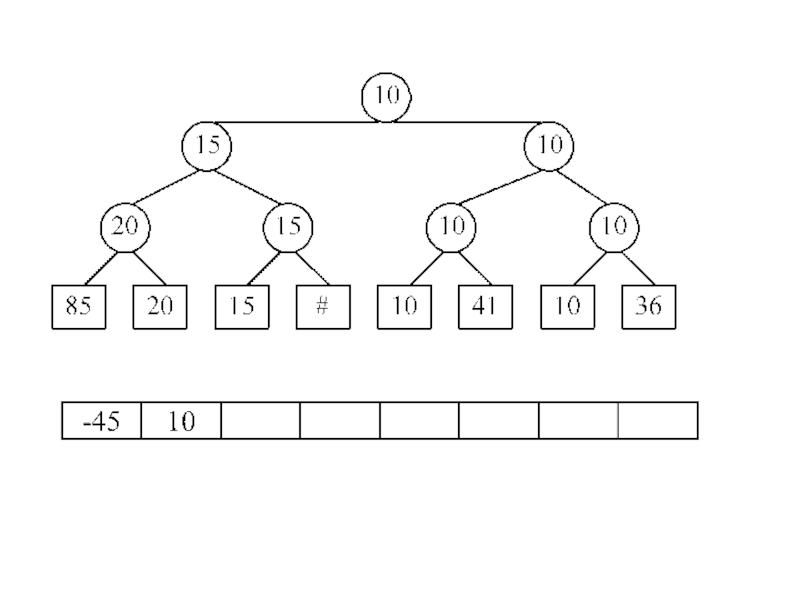
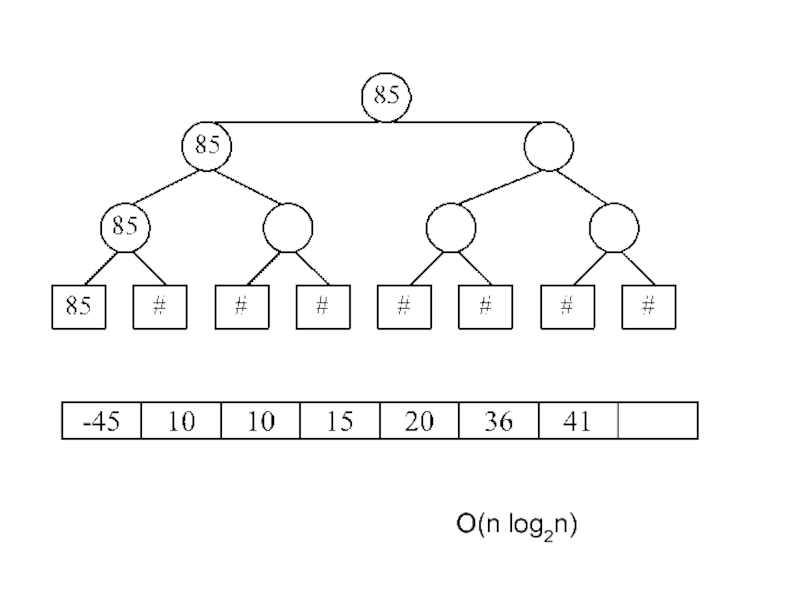
- 26. Турнирная сортировка A[8]={85, 20, 15, -45, 10, 41, 10, 36} 2k≥N k=3
- 29. O(n log2n)
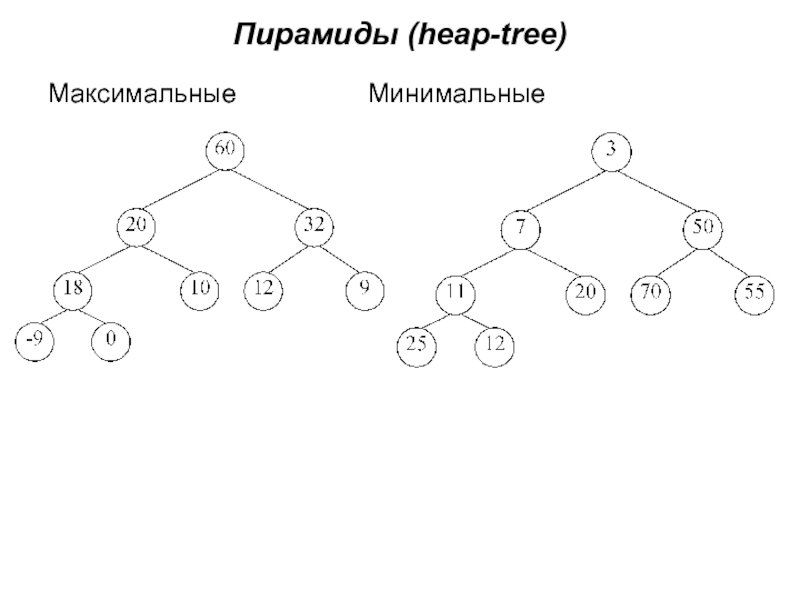
- 30. Пирамиды (heap-tree) Максимальные Минимальные
- 31. Преобразование массива в пирамиду n n-1 (n-2)/2 Пример: Построим
- 32. H[4]=9 H[9]=86 H[3]=43 H[8]=72 H[7]=30 H[2]=72 H[5]=47
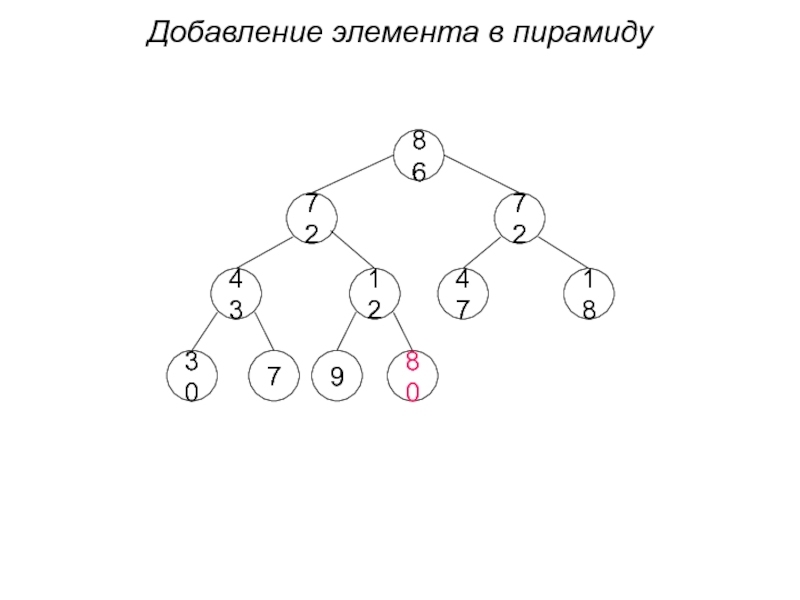
- 33. Добавление элемента в пирамиду 86 72 72 43 12 47 18 30 9 7 80
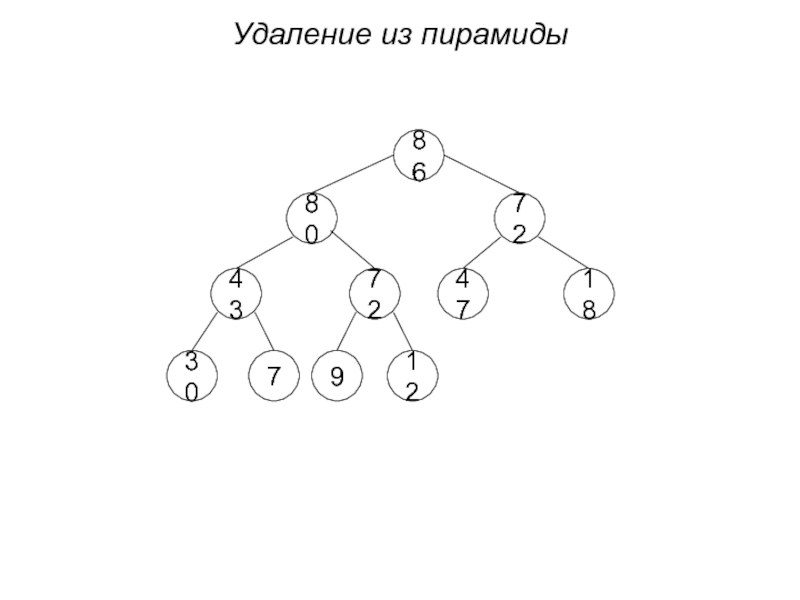
- 34. Удаление из пирамиды 86 80 72 43 72 47 18 30 9 7 12
- 35. Пирамидальная сортировка Пример: int A[]={54, 21, 90,
- 36. Сбалансированные деревья AVL struct AVLTREE{
Слайд 4Двоичные (бинарные) деревья
{R} - корневой узел
{L1, L2, ..., Lm} - левое
{R1, R2, ..., Rm} - правое поддерево R
n
1 … 2n
Слайд 6Структура двоичного дерева
С использованием массива
TREE[n];
TREE[K] - TREE[2K+1], TREE[2K+2]
В виде динамической структуры
struct
int dann;
TREE *pleft;
TREE *pright;
};
Слайд 7Идеально сбалансированное дерево
Взять один узел в качестве корня.
Левое поддерево: nl=n/2.
Правое поддерево:
Пример: 6, 4, 2, 3, 8, 9, 0, 1, 7
Слайд 8TREE* maketree(int n)
{TREE *ptr;
int nl, nr, x;
if (n==0) return NULL;
nl=n/2;
nr=n-nl-1;
ptr=new (TREE);
cout
cin >> ptr->dann;
ptr->pleft=maketree(nl);
ptr->pright=maketree(nr);
return ptr;
}
TREE *root;
root=maketree(n);
void print(TREE *ptr, int h)
{
if (ptr) {
print(ptr->pright,h+1);
for (int i=1;i<=h;i++) cout << " ";
cout << ptr->dann << endl;
print(ptr->pleft,h+1);
}
}
Слайд 12void build(TREE *tt, char ch)
{
if (chdann)
if (tt->pleft==NULL)
tt->pleft=left;
left->dann=ch;
left->pleft=NULL;
left->pright=NULL;
}
else build(tt->pleft,ch);
else
if (tt->pright==NULL)
{right=new TREE;
tt->pright=right;
right->dann=ch;
right->pleft=NULL;
right->pright=NULL;
}
else build(tt->pright,ch);
}
root=new TREE;
root->dann=str[0];
root->pright=NULL;
root->pleft=NULL;
for (int i=1; i
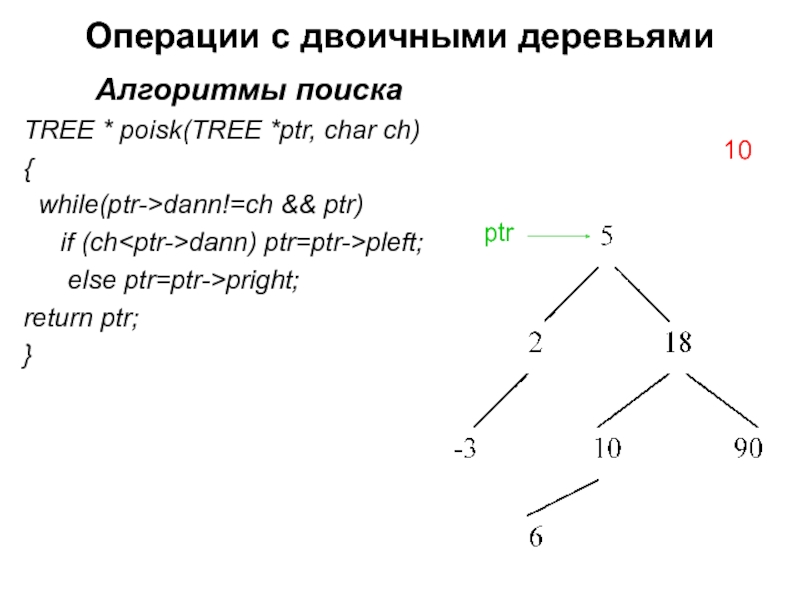
Слайд 13Операции с двоичными деревьями
Алгоритмы поиска
TREE * poisk(TREE *ptr, char ch)
{
while(ptr->dann!=ch
if (ch
else ptr=ptr->pright;
return ptr;
}
10
Слайд 14TREE *parent=NULL; TREE *find(char x, TREE* ptr) { while (ptr!=NULL) { if (x==ptr->dann)
TREE * poisk(TREE *ptr, char ch,)
{
if (ch
if (ch>ptr->dann) ptr=poisk(ptr->pright, ch);
else return ptr;
}
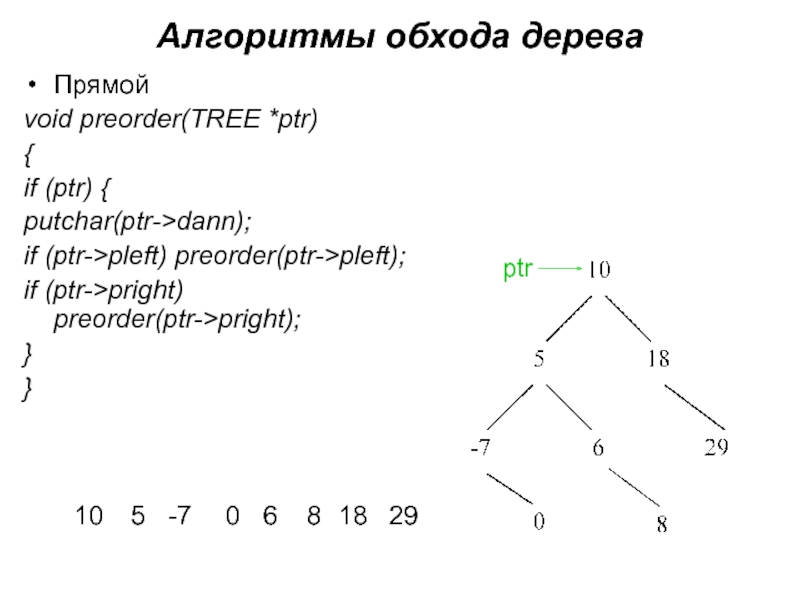
Слайд 15Алгоритмы обхода дерева
Прямой
void preorder(TREE *ptr)
{
if (ptr) {
putchar(ptr->dann);
if (ptr->pleft) preorder(ptr->pleft);
if (ptr->pright) preorder(ptr->pright);
}
}
10
5
-7
0
6
8
18
29
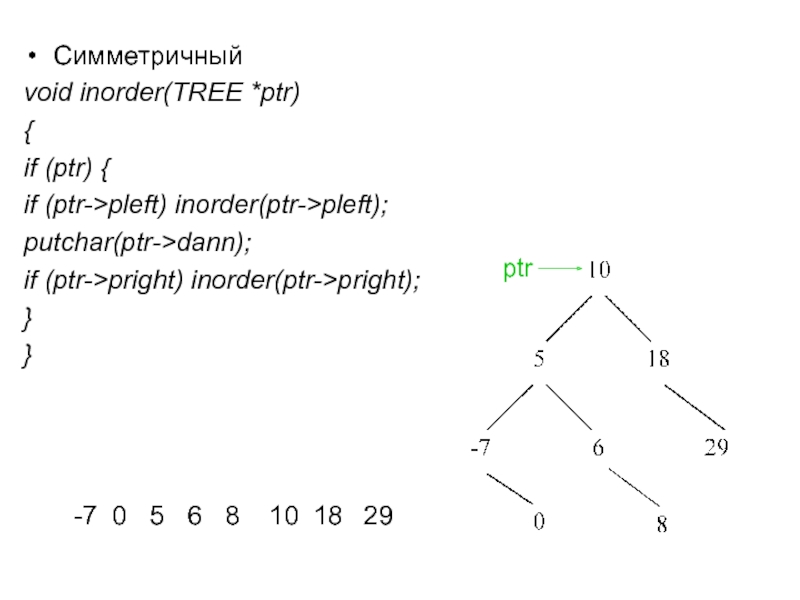
Слайд 16Симметричный
void inorder(TREE *ptr)
{
if (ptr) {
if (ptr->pleft) inorder(ptr->pleft);
putchar(ptr->dann);
if (ptr->pright) inorder(ptr->pright);
}
}
-7
0
5
6
8
10
18
29
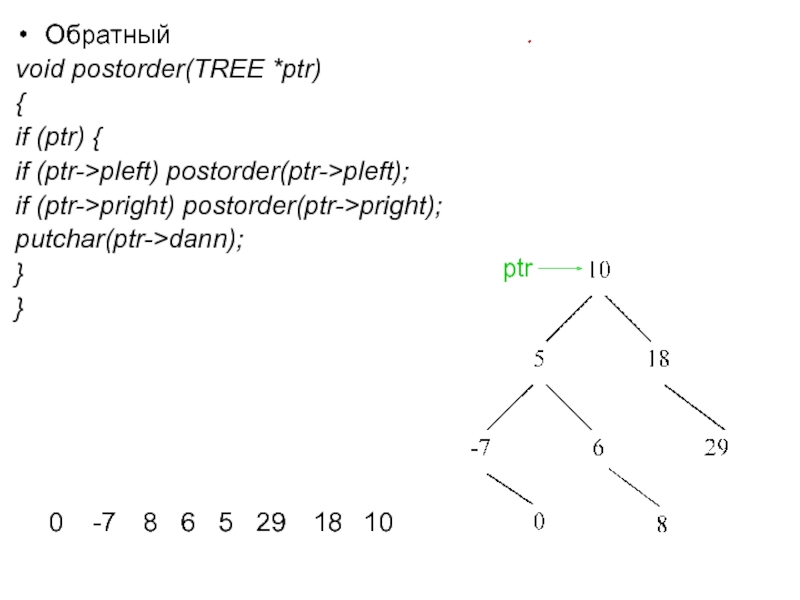
Слайд 17Обратный
void postorder(TREE *ptr)
{
if (ptr) {
if (ptr->pleft) postorder(ptr->pleft);
if (ptr->pright) postorder(ptr->pright);
putchar(ptr->dann);
}
}
0
-7
8
6
5
29
18
10
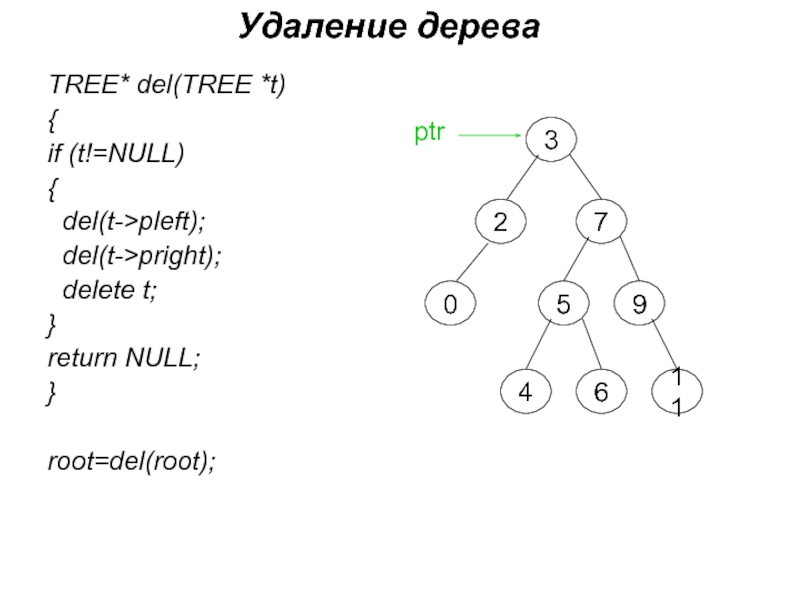
Слайд 19Удаление дерева
TREE* del(TREE *t)
{
if (t!=NULL)
{
del(t->pleft);
del(t->pright);
delete t;
}
return NULL;
}
root=del(root);
3
2
7
0
5
9
4
6
11
Слайд 20Удаление элемента из дерева
Элемента со значением, равным х, в дереве не
Элемент со значением х является терминальным узлом;
Элемент со значением х имеет одного потомка;
3
2
7
0
5
9
4
6
11
3
2
7
0
5
9
4
6
11
Слайд 24Двоичные деревья, представляемые массивами
A[i]
Индекс левого наследника = 2*i+1.
Индекс правого наследника
Индекс родителя = (i-1)/2.
Пример:
int A[]={5, 1, 3, 9, 6, 2, 4, 7, 0, 8};
Слайд 31Преобразование массива в пирамиду
n n-1 (n-2)/2
Пример: Построим максимальную пирамиду
int H[10]={7, 12, 72, 43,
5, 6, …, 9
4, 3, …, 0
Слайд 32H[4]=9
H[9]=86
H[3]=43
H[8]=72 H[7]=30
H[2]=72
H[5]=47 H[6]=18
H[1]=12
H[3]=72 H[4]=86
H[0]=7
H[1]=86 H[2]=72
7
12
72
43
9
47
18
30
86
72
Слайд 36Сбалансированные деревья
AVL
struct AVLTREE{
int dann;
int balance;
AVLTREE
AVLTREE *pright;
};
balance<0
balance=0
balance>0
![Структура двоичного дереваС использованием массива TREE[n]; TREE[K] - TREE[2K+1], TREE[2K+2]В виде динамической структурыstruct TREE{ int](/img/tmb/4/369772/2fe40b88fb6efaad59b7fefc5b0f75eb-800x.jpg)




![Двоичные деревья, представляемые массивамиA[i] Индекс левого наследника = 2*i+1.Индекс правого наследника = 2*i+2.Индекс родителя =](/img/tmb/4/369772/dc346a5dd86ee0070abe3bb274dec6ff-800x.jpg)
![int A[]={5, 1, 3, 9, 6, 4, #, 7, #, #, #, 2};](/img/tmb/4/369772/8724fc1acab94920ebe574984fdd47de-800x.jpg)
![Турнирная сортировкаA[8]={85, 20, 15, -45, 10, 41, 10, 36}2k≥Nk=3](/img/tmb/4/369772/91d3d4bb7cd73f2646694f6628b1f8ab-800x.jpg)
![Преобразование массива в пирамидуn n-1 (n-2)/2Пример: Построим максимальную пирамидуint H[10]={7, 12, 72, 43, 9, 47, 18, 30,](/img/tmb/4/369772/655cd857b3411bba001fbf0cd0fc9eb4-800x.jpg)
![H[4]=9H[9]=86H[3]=43H[8]=72 H[7]=30H[2]=72H[5]=47 H[6]=18H[1]=12H[3]=72 H[4]=86H[0]=7H[1]=86 H[2]=72712724394718308672](/img/tmb/4/369772/417ea2af9942630f96efb0031b29c0f8-800x.jpg)
![Пирамидальная сортировкаПример: int A[]={54, 21, 90, 38, 23, 0};542190382300212338n log2n](/img/tmb/4/369772/2d929ec72e29879a768687e3f2e167c5-800x.jpg)