- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Численное интегрирование презентация
Содержание
- 1. Численное интегрирование
- 2. Задача численного интегрирования сводится к нахождению численного
- 3. Численное интегрирование методом прямоугольников имеет три разновидности:
- 4. Метод левых прямоугольников Формула вычисления интеграла методом левых прямоугольников
- 5. Пример. Вычислить интеграл методом левых прямоугольников Метод левых прямоугольников
- 6. При вычислении интеграла методом правых прямоугольников
- 7. Метод правых прямоугольников Формула вычисления интеграла методом правых прямоугольников
- 8. Пример. Вычислить интеграл методом правых прямоугольников Метод правых прямоугольников
- 9. При вычислении интеграла методом правых прямоугольников
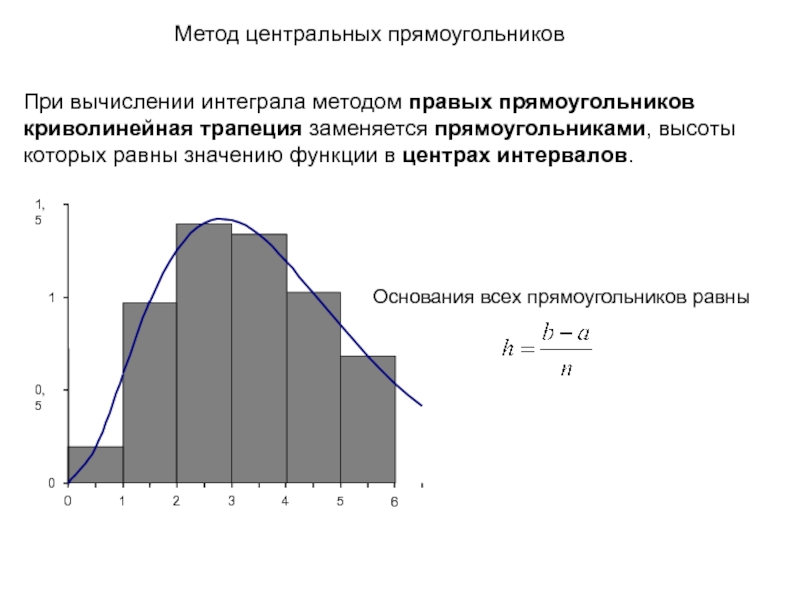
- 10. Метод центральных прямоугольников Формула вычисления
- 11. Пример. Вычислить интеграл методом центральных прямоугольников Метод правых прямоугольников
- 12. При вычислении интеграла методом трапеций криволинейная
- 13. Метод трапеций Формула вычисления интеграла
- 14. Пример. Вычислить интеграл методом трапеций Метод трапеций
- 15. При вычислении интеграла методом парабол криволинейная
- 16. Метод парабол
- 17. Метод парабол
- 18. Коэффициенты параболы определяются из условия прохождения
- 21. Метод парабол Формула вычисления интеграла
- 22. Пример. Вычислить интеграл методом парабол Метод парабол
- 23. При вычислении интеграла методом Симпсона 3/8
- 24. Пример. Вычислить интеграл методом Симпсона 3/8
- 25. При вычислении интеграла методом Буля криволинейная
- 26. Степенью точности называют такое целое число n,
- 27. 6.4.6. Сравнение различных методов по точности
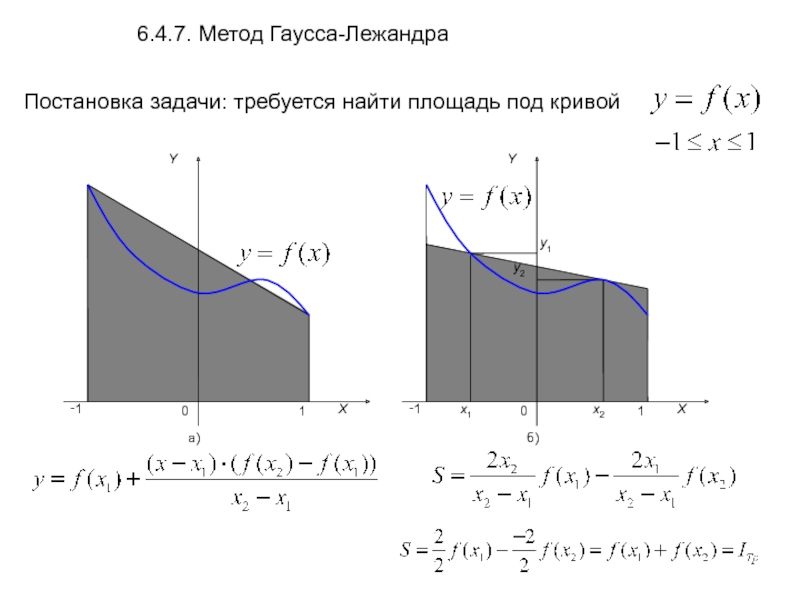
- 28. Постановка задачи: требуется найти площадь под
- 29. Согласно методу Гаусса-Лежандра приближенное значение интеграла определяется
- 32. Пример. Вычислить интеграл методом Гаусса-Лежандра по 2
- 33. Если требуется вычислить значение интеграла на интервале
- 34. Если требуется вычислить значение интеграла на интервале
- 35. При вычислении интеграла методом Гаусса-Лежандра по трем
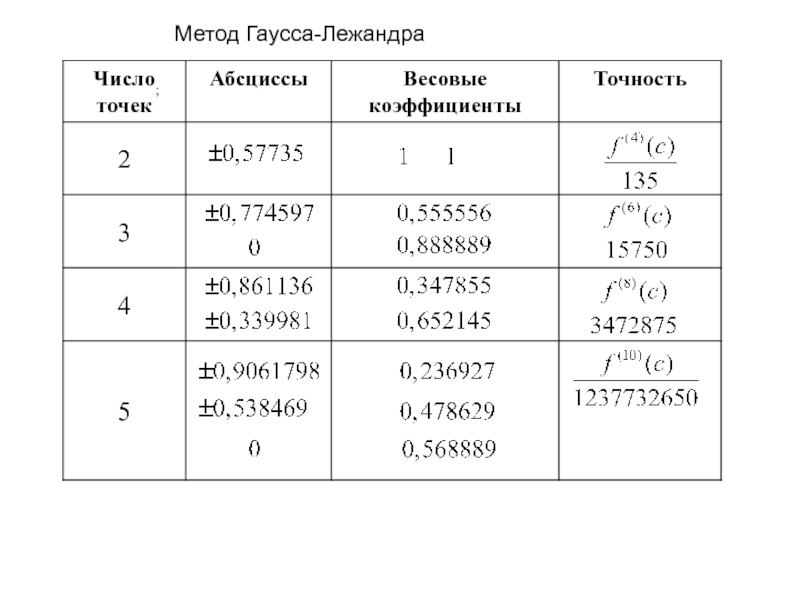
- 36. Метод Гаусса-Лежандра ;
- 37. Николас Константин Метрополис, Станислав Мартин Улам
- 38. u – случайная величина, равномерно распределенная на
- 39. 6.4.8. Метод Монте-Карло Формула вычисления интеграла простейшим методом Монте-Карло
- 40. Геометрический метод Монте-Карло
- 41. Достоинства
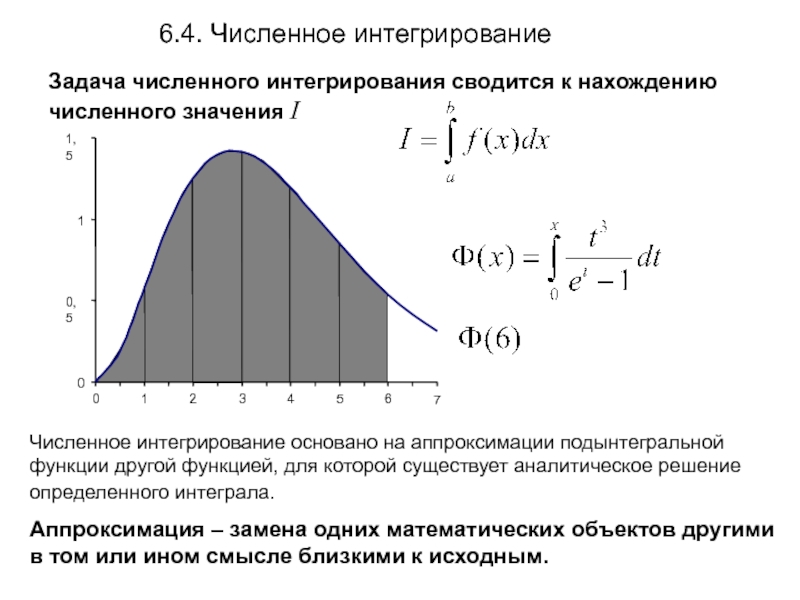
Слайд 2Задача численного интегрирования сводится к нахождению численного значения I
6.4. Численное интегрирование
Численное
Аппроксимация – замена одних математических объектов другими в том или ином смысле близкими к исходным.
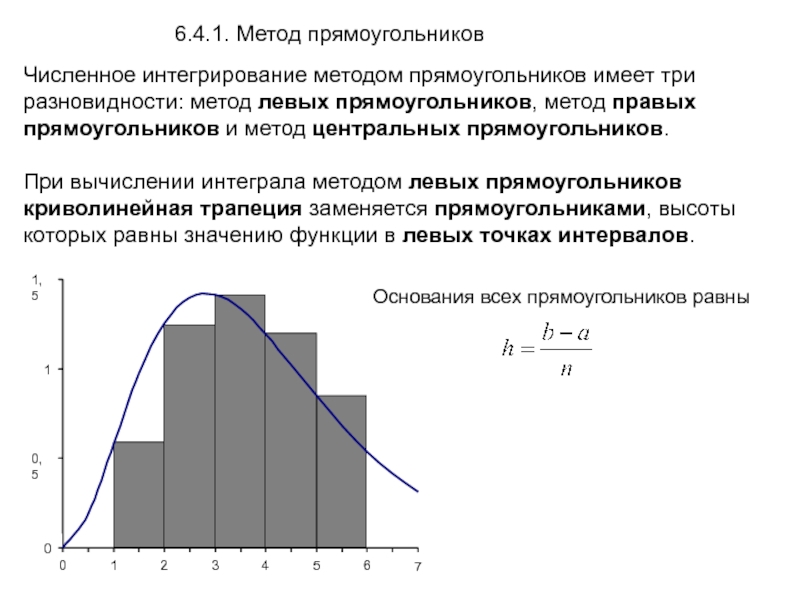
Слайд 3Численное интегрирование методом прямоугольников имеет три разновидности: метод левых прямоугольников, метод
При вычислении интеграла методом левых прямоугольников криволинейная трапеция заменяется прямоугольниками, высоты которых равны значению функции в левых точках интервалов.
6.4.1. Метод прямоугольников
Основания всех прямоугольников равны
Слайд 6
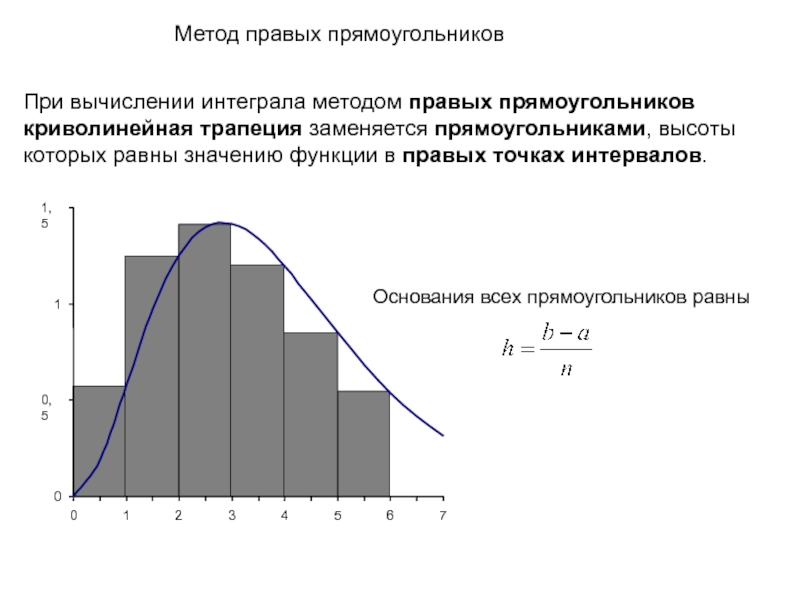
При вычислении интеграла методом правых прямоугольников криволинейная трапеция заменяется прямоугольниками, высоты
Метод правых прямоугольников
Основания всех прямоугольников равны
Слайд 9
При вычислении интеграла методом правых прямоугольников криволинейная трапеция заменяется прямоугольниками, высоты
Метод центральных прямоугольников
Основания всех прямоугольников равны
Слайд 10
Метод центральных прямоугольников
Формула вычисления интеграла методом центральных прямоугольников
Слайд 12
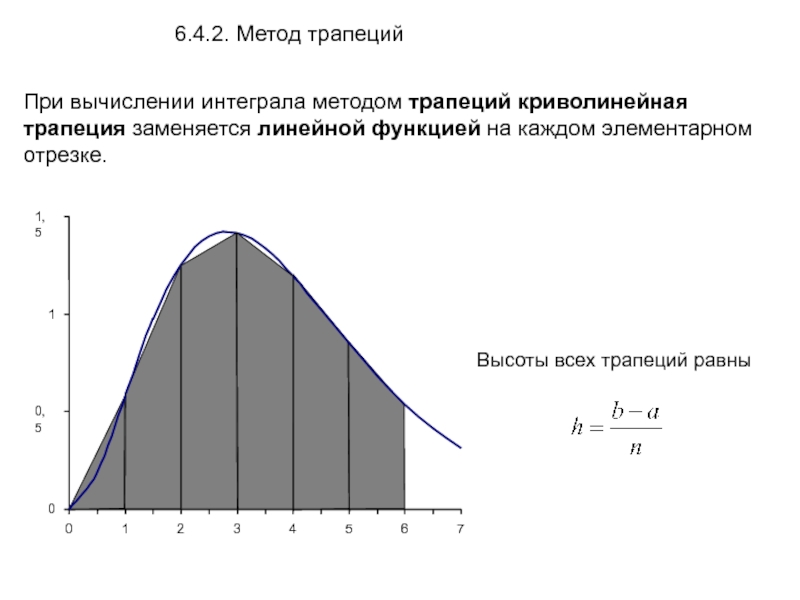
При вычислении интеграла методом трапеций криволинейная трапеция заменяется линейной функцией на
6.4.2. Метод трапеций
Высоты всех трапеций равны
Слайд 15
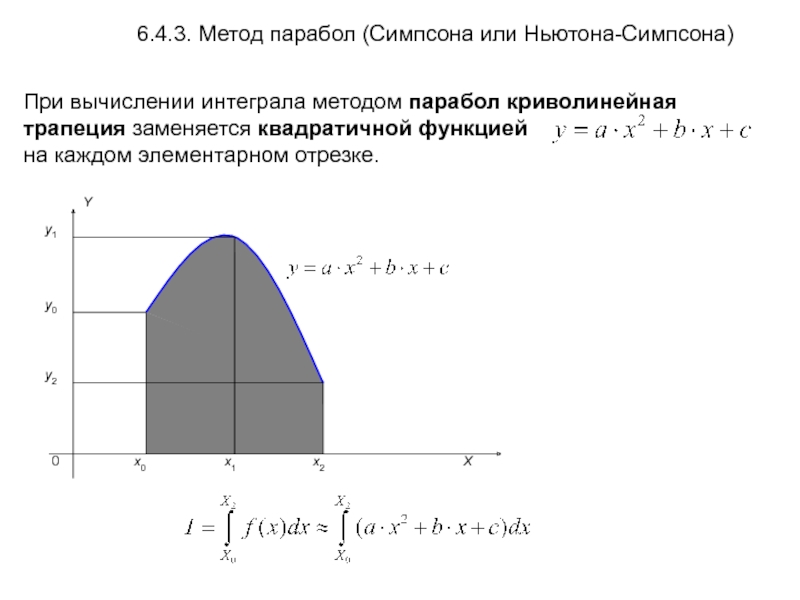
При вычислении интеграла методом парабол криволинейная трапеция заменяется квадратичной функцией
на
6.4.3. Метод парабол (Симпсона или Ньютона-Симпсона)
Слайд 23
При вычислении интеграла методом Симпсона 3/8 криволинейная трапеция на каждом элементарном
6.4.4. Метод Симпсона 3/8
Формула вычисления интеграла методом Симпсона 3/8
(n кратно 3)
Слайд 25
При вычислении интеграла методом Буля криволинейная трапеция на каждом элементарном отрезке
6.4.5. Метод Буля
Формула вычисления интеграла методом Буля
(n кратно 4)
Слайд 26Степенью точности называют такое целое число n, что для всех полиномов
6.4.6. Сравнение различных методов по точности приближения
– численное значение интеграла,
полученное тем или иным методом
– ошибка интегрирования, которая зависит от
вида функции f(x) и шага h
Слайд 29Согласно методу Гаусса-Лежандра приближенное значение интеграла определяется с помощью весового суммирования
6.4.7. Метод Гаусса-Лежандра
Значения абсцисс x1 и x2 и весов ω1 и ω2 выбираются из условия, что данная формула будет точной для четырех функций: f(x)=1, x, x2, и x3.
Слайд 33Если требуется вычислить значение интеграла на интервале [a; b], то требуется
Метод Гаусса-Лежандра
Пример. Вычислить интеграл
Слайд 34Если требуется вычислить значение интеграла на интервале [a; b], то требуется
Метод Гаусса-Лежандра
Пример. Вычислить интеграл
Слайд 35При вычислении интеграла методом Гаусса-Лежандра по трем точкам приближенное значение определяется
Значения абсцисс x1, x2 и x3 и весов ω1, ω2 и ω3 выбираются из условия, что данная формула будет точной для шести функций: f(x) = 1, x, x2, x3, x4, и x5.
Слайд 37Николас Константин Метрополис,
Станислав Мартин Улам – авторы статьи
«Метод Монте-Карло»
6.4.8. Метод Монте-Карло
Слайд 38u – случайная величина, равномерно распределенная на интервале [a; b]
6.4.8. Метод
– плотность распределения случайная величины u
Слайд 40
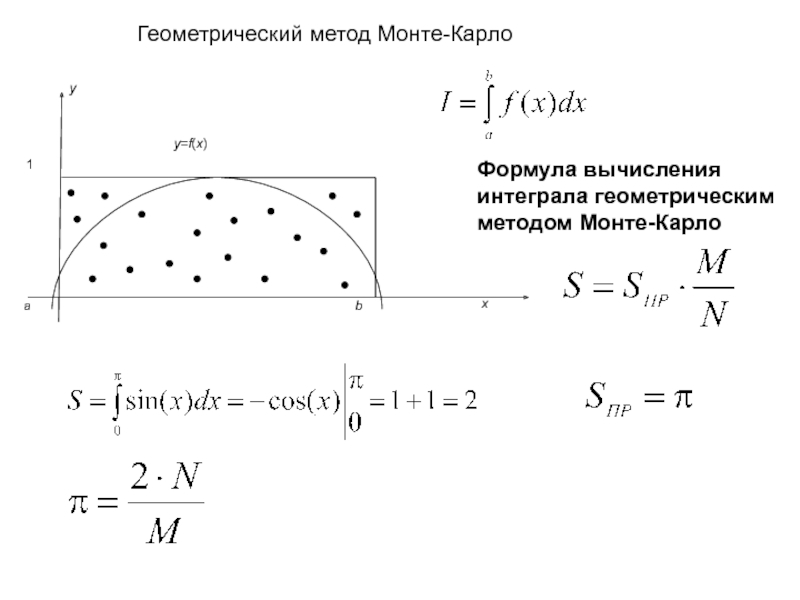
Геометрический метод Монте-Карло
Формула вычисления интеграла геометрическим методом Монте-Карло
Слайд 41
Достоинства метода Монте-Карло:
простую структуру вычислительного алгоритма;
вычисления значения интеграла можно
погрешность вычислений не реагирует на размерность задачи;
при вычислении многомерных интегралов метод Монте-Карло остается единственным, способным выдать приближенное значение за конечное время.
Недостатки метода Монте-Карло:
при вычислении одномерных интегралов сходимость метода уступает регулярным методам;
для уменьшения погрешности на порядок, необходимо увеличить количество испытаний на два порядка.
Простейший метод всегда точнее геометрического.












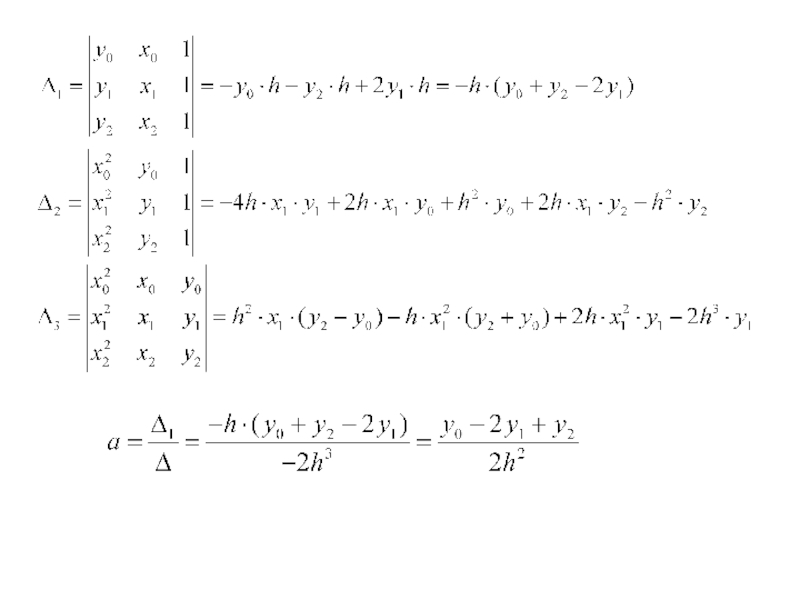
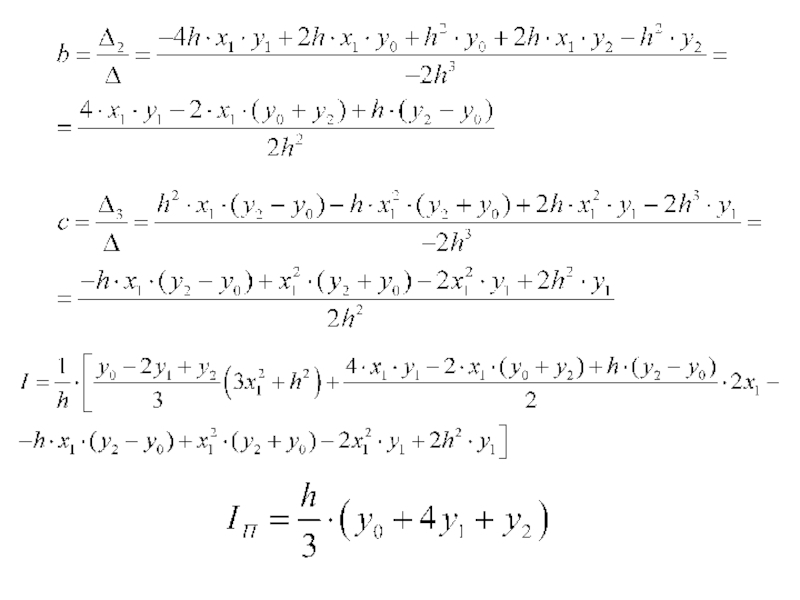








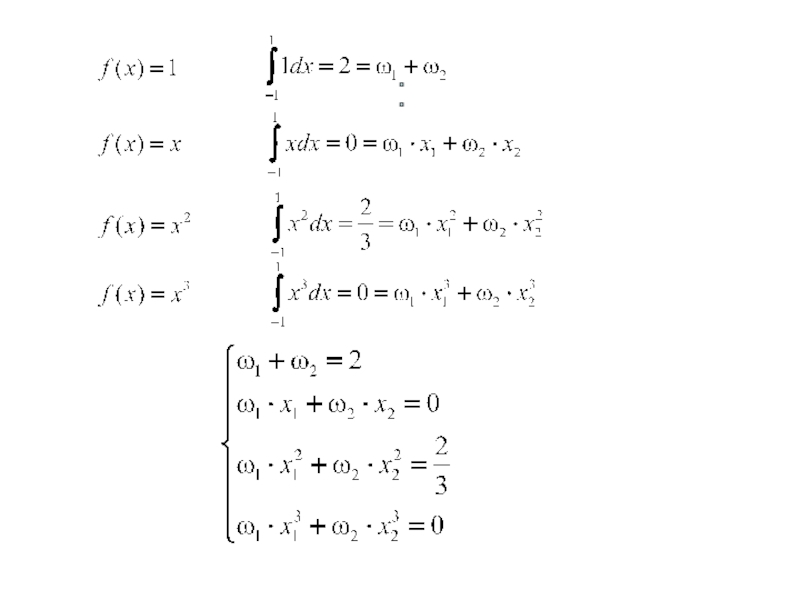
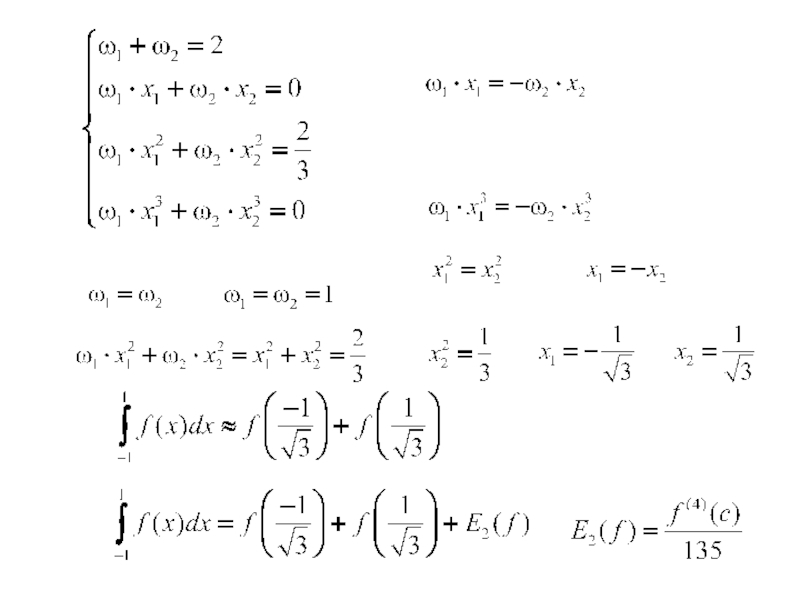

![Если требуется вычислить значение интеграла на интервале [a; b], то требуется выполнить замену переменнойМетод Гаусса-Лежандра](/img/tmb/4/321297/ea73b5da7a8d221cc1cb08b9f73c0108-800x.jpg)
![Если требуется вычислить значение интеграла на интервале [a; b], то требуется выполнить замену переменнойМетод Гаусса-Лежандра](/img/tmb/4/321297/c6545d00fe8c5998884709f2ff4f0f17-800x.jpg)


![u – случайная величина, равномерно распределенная на интервале [a; b]6.4.8. Метод Монте-Карло– плотность распределения случайная](/img/tmb/4/321297/081d55cf4e9ffe285c9cf0fa8903816e-800x.jpg)