- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Базовые логические функции. Основные понятия алгебры логики презентация
Содержание
- 1. Базовые логические функции. Основные понятия алгебры логики
- 2. Основные понятия алгебры логики Алгебры логики
- 3. логическая переменная это такая переменная, которая может
- 4. Логическая функция Логическая функция может быть одного
- 5. Задание логической функции Зависимость логической функции от
- 6. Таблица истинности Таблица истинности для нескольких функций
- 7. Логическое выражение Логическим выражением называется комбинация логических
- 8. Булевый базис. Набор элементарных логических операций, с
- 9. Основные законы алгебры Буля В алгебре Буля
- 10. Основные законы алгебры Буля Сочетательный (ассоциативный) закон.
- 11. Правило де Моргана
- 12. Операция склеивания Операция склеивания:
- 13. Формы представления логических выражений Одну и туже
- 14. СДНФ СДНФ - Совершенная дизъюнктивная нормальная форма
- 15. СКНФ Совершенная конъюнктивная нормальная форма это
- 16. Минимизация логических выражений Учитывая то, что одну
- 17. Карты Карно - Вейча Карта Карно для
- 18. Этапы минимизации Для выполнения минимизации представленной
- 19. Логическими соседями являются такие две клетки, наборы
- 20. Логические соседи Карта является пространственным объектом и
- 21. Логические соседи Логическими соседями могут быть
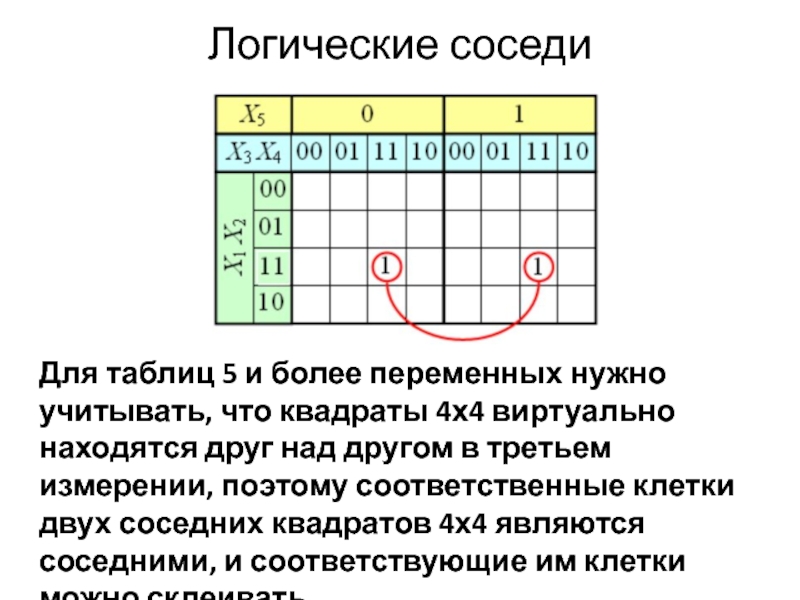
- 22. Логические соседи Для таблиц 5 и более
- 23. Правила охвата клеток Охват клеток карты контурами
- 24. Правила записи Запись минимального выражения заданной функции
- 25. Функциональные узлы ЭВМ комбинационного типа
- 26. Шифратор Шифратор (кодер) - это устройство, преобразующее
- 27. Шифратор Предположим, на пульте десять клавиш с
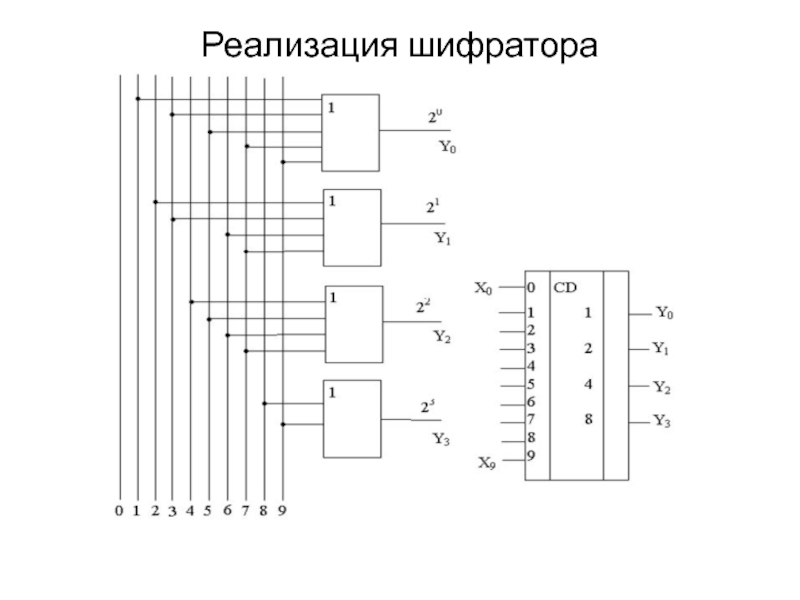
- 28. Реализация шифратора
- 29. Дешифраторы Дешифратор (декодер) - устройство, преобразующее n
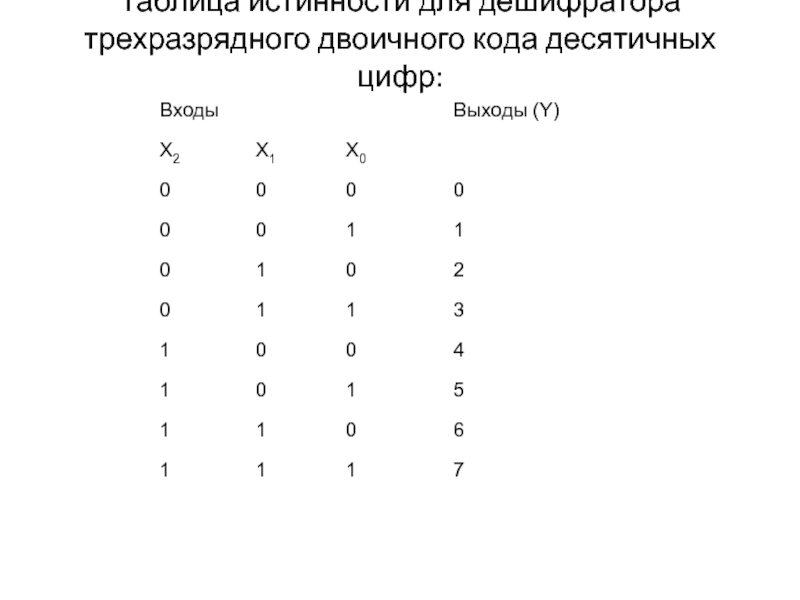
- 30. Таблица истинности для дешифратора трехразрядного двоичного кода десятичных цифр:
- 31. Дешифратор на три входа
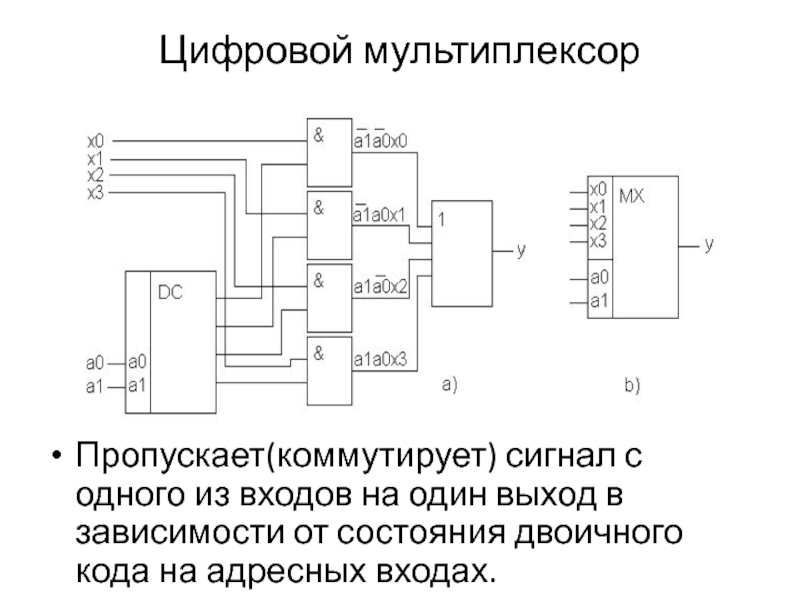
- 32. Цифровой мультиплексор Пропускает(коммутирует) сигнал с одного из
- 33. Цифровой компаратор Сравнивает два двоичных числа http://naf-st.ru/articles/digit/sum/
- 34. Сложе́ние по мо́дулю 2 (исключа́ющее «ИЛИ»)
- 35. Одноразрядный двоичный сумматор PI – перенос из
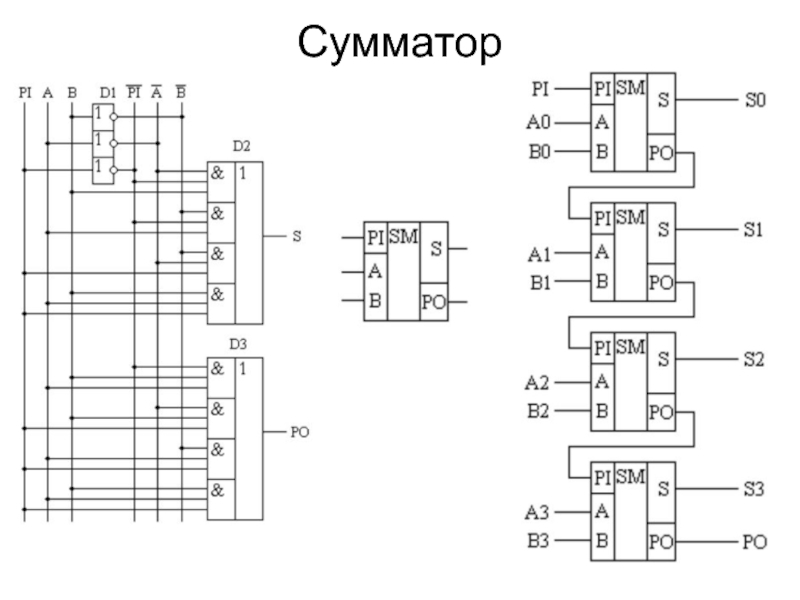
- 36. Сумматор
- 37. Функциональные узлы ЭВМ последовательного типа (элементы с памятью)
- 38. Составляющие цифрового сигнала 1 — низкий уровень
- 39. Асинхронный RS - триггер RS-триггер - устройство
- 40. Синхронный D-триггер Когда на вход С подан
- 41. Т- триггеры Т – триггеры работают
- 42. Регистр Каждый D - триггер служит для
- 43. Регистр сдвига Каждый выход триггера соединен с
- 44. Цифровой счетчик Цифровой счетчик импульсов -
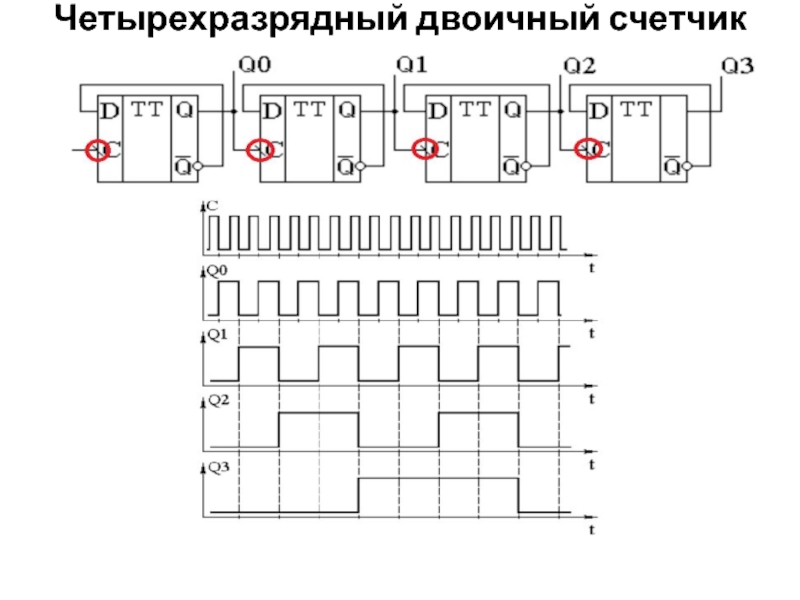
- 45. Четырехразрядный двоичный счетчик
- 46. Цифровой счетчик Используются следующие разновидности счетчика: -
Слайд 2Основные понятия алгебры логики
Алгебры логики - раздел математической логики, в котором
Алгебра логики находят широкое применение при синтезе и анализа схем ЭВМ, так как информация представляется в двоичном виде и реализуется с помощью физических элементов которые могут пропускать или не пропускать ток, иметь на выходе высокий или низкий уровень сигнала (напряжения или тока – ноль или единицу) .
Слайд 3логическая переменная это такая переменная, которая может принимать одно из двух
логическая константа это такая постоянная величина, значением которой может быть: истинно или ложно (да или нет, единица или ноль).
логическая функция это такая функция, которая может принимать одно из двух значений (истинно или ложно, да или нет, единица или ноль), в зависимости от текущего значений её аргументов, в качестве которых используются логические переменные.
Основные понятия алгебры логики
Слайд 4Логическая функция
Логическая функция может быть одного (n=1) или нескольких (n
N= 2n.
Слайд 5Задание логической функции
Зависимость логической функции от переменных может задаваться:
Словесным описанием, как
Таблицой истинности является универсальным средством задания логической функции. Она включает все наборы для заданного количества переменных, определяющих значение логической функции, с указанием значений, которые принимает функция для каждого набора. В одной таблицы истинности может задаваться несколько логических функций, зависящих от одних и тех же переменных
В виде логического выражения.
.
Слайд 6Таблица истинности
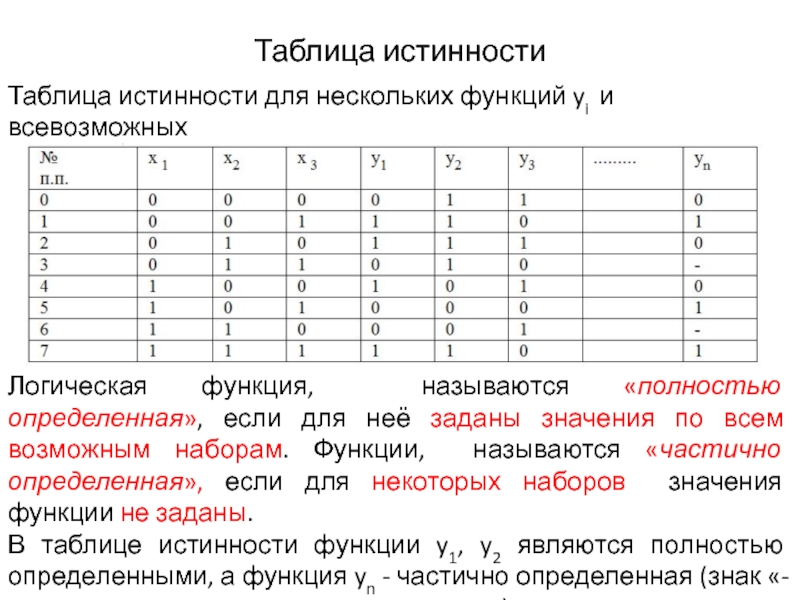
Таблица истинности для нескольких функций yi и всевозможных
наборов
Логическая функция, называются «полностью определенная», если для неё заданы значения по всем возможным наборам. Функции, называются «частично определенная», если для некоторых наборов значения функции не заданы.
В таблице истинности функции y1, y2 являются полностью определенными, а функция yn - частично определенная (знак «-» означает неопределенность значения).
Слайд 7Логическое выражение
Логическим выражением называется комбинация логических переменных и констант, связанных элементарными
Например, логическую функцию у1, определенную выше приведенной таблице истинности, можно представить в виде логического выражения:
где « ͞ », «+», «*» - знаки базовых логических функций
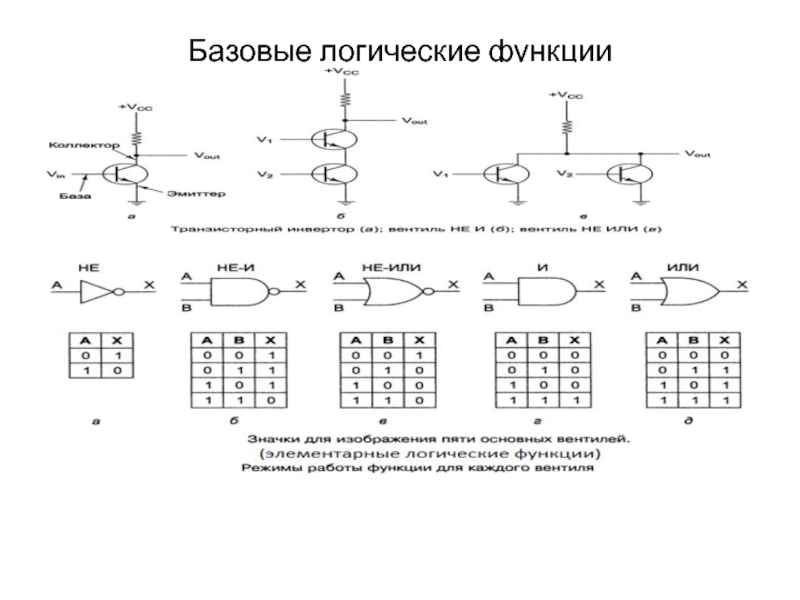
Слайд 8Булевый базис.
Набор элементарных логических операций, с помощью которого можно задать любую,
Наиболее распространенный, который в качестве базовых логических функций использует функцию одной переменной « НЕ» ( функция отрицания), и две функции двух переменных «И» (конъюнкция или логическое умножения) и «ИЛИ» (дизъюнкция или логическое сложение). Эта система получила название система Булевых функций или Булевый базис.
Слайд 9Основные законы алгебры Буля
В алгебре Буля используется следующая приоритетность выполнения операций:
-
- затем выполняются операция И (логическое умножение);
- самый низший приоритет имеет операция ИЛИ ( логическая сумма).
При работе с булевыми логическим выражениями используются следующие законы и правила.
Переместительный (коммутативный) закон. Закон справедлив как для конъюнкции, так и для дизъюнкции.
х1 + х2 + х3 + х4 .= х4 + х3 + х2+ х1 - от перемены мест логических слагаемых сумма не меняется;
х1 * х2 * х3 * х4 .= х4 * х3 * х2* х1 - от перемены мест логических сомножителей их произведение не меняется.
Слайд 10Основные законы алгебры Буля
Сочетательный (ассоциативный) закон. Закон справедлив как для конъюнкции,
х1 + х2 + х3 + х4.= (х2 + х3 )+ х1 + х4.=( х1 + х4 )+ (х2 + х3) - при логическом сложения отдельные слагаемые можно заменить их суммой;
х1 * х2 * х3 * х4.= (х2 * х3) )* х1 * х4.=( х1 * х4)* (х2 * х3) - при логическом умножении отдельные логические сомножители можно заменить их произведением.
Распределительный (дистрибутивный) закон.
(х1 + х2 )* х3 .= х1 * х3 + х2* х3.
(х1 + х2 )*( х1 + х3)= х1 + х2* х3.
Слайд 11Правило де Моргана
-
-отрицание произведения равно сумме отрицаний. Правило справедливо при любом числе логических операндов.
Слайд 12Операция склеивания
Операция склеивания:
-
=А - операция склеивания для дизъюнкций,
Операции с отрицаниями:
x - двойное отрицание равносильно
отсутствию отрицания;
Слайд 13Формы представления логических выражений
Одну и туже логическую функцию можно представить различными
совершенная конъюнктивная нормальная форма (СКНФ),
совершенная дизъюнктивная нормальная форма (СДНФ).
Совершенная дизъюнктивная нормальная форма представляет собой дизъюнкцию простых конъюнкций, где под термином простая конъюнкция имеется в виду конъюнкция переменных или их отрицаний.
Слайд 14СДНФ
СДНФ - Совершенная дизъюнктивная нормальная форма представляет собой дизъюнкцию простых конъюнкций
В СДНФ простые конъюнкции содержат все переменные в своей прямой или инверсной форме и отражают собой наборы, на которых представляемая функция имеет единичное значение. Такие конъюнкции называются конституентами единицы рассматриваемой функции.
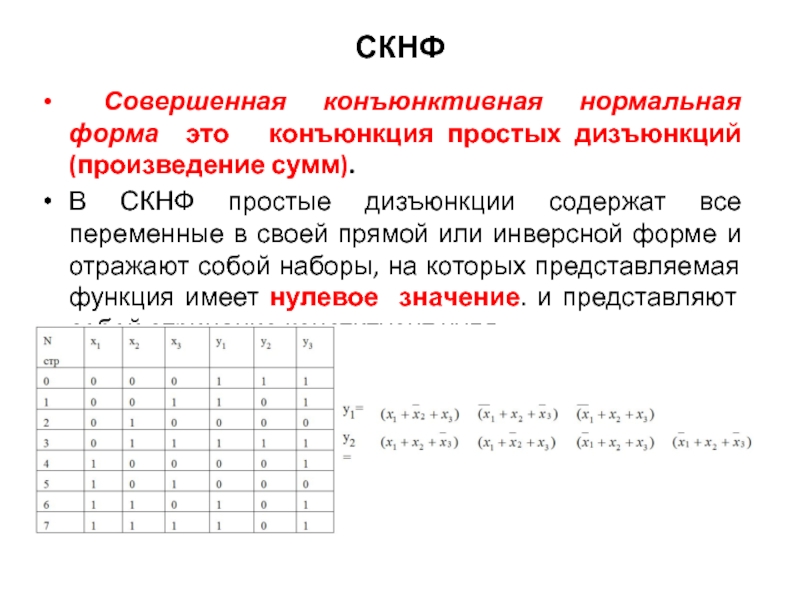
Слайд 15СКНФ
Совершенная конъюнктивная нормальная форма это конъюнкция простых дизъюнкций(произведение сумм).
В
Слайд 16Минимизация логических выражений
Учитывая то, что одну и ту же логическую функцию
Слайд 17Карты Карно - Вейча
Карта Карно для «n» логических переменных представляет собой
Карта Карно задает своего рода таблицу истинности.
Записываемая функция должна быть представлена в СДНФ(СКНФ). Запись функции в карту осуществляется за счет установки «1»(0 - СКНФ) в те клетки карты, где функция принимает единичное (нулевое) значение.
Слайд 18
Этапы минимизации
Для выполнения минимизации представленной в карте Карно функции необходимо выполнить
охватить множество клеток карты Карно контурами;
записать минимальное выражение для заданной функции в виде дизъюнкции конъюнкций для СДНФ (или конъюнкция дизъюнкций для СКНФ), где каждая конъюнкция (дизъюнкция) соответствует одному из введенных на карте контуров.
Слайд 19Логическими соседями являются такие две клетки, наборы которых отличаются только одной
Для того, чтобы быть логическими соседями, клеткам достаточно быть геометрическими соседями.
Логические соседи
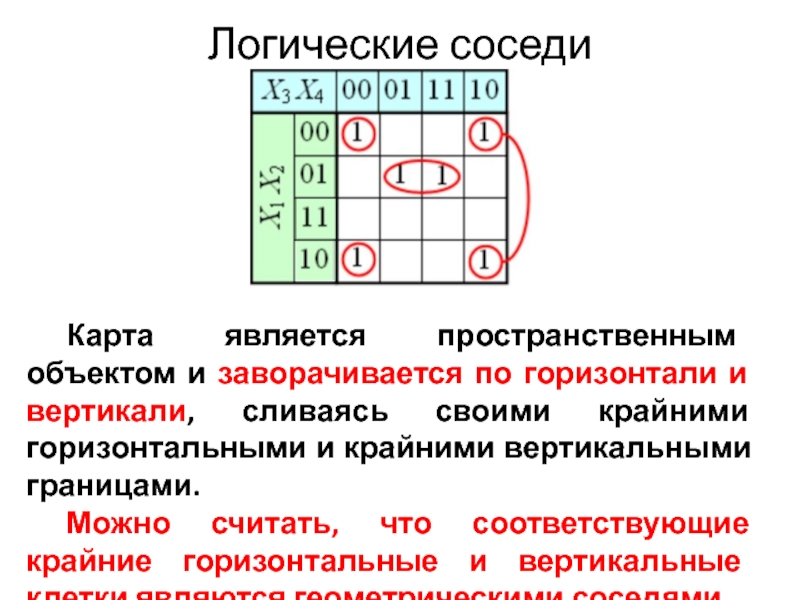
Слайд 20Логические соседи
Карта является пространственным объектом и заворачивается по горизонтали и вертикали,
Можно считать, что соответствующие крайние горизонтальные и вертикальные клетки являются геометрическими соседями.
Слайд 21Логические соседи
Логическими соседями могут быть клетки, которые не являются геометрическими
Слайд 22Логические соседи
Для таблиц 5 и более переменных нужно учитывать, что квадраты
Слайд 23Правила охвата клеток
Охват клеток карты контурами выполняется с соблюдением следующих правил:
контурами
контур должен иметь прямоугольную форму;
в контур может входить такое количество клеток, которое равно целой степени числа «2»;
в контур могут входить клетки, являющиеся логическими соседями;
в контур необходимо включить максимальное количество клеток с учетом выше приведенных требований;
контуров должно быть минимальное количество.
Слайд 24Правила записи
Запись минимального выражения заданной функции имеет вид дизъюнкции простых конъюнкций
- соответствующая контуру конъюнкция (дизъюнкция для СКНФ), должна включать, только те переменные, которые имеют постоянное значение во всех клетках, охваченных рассматриваемым контуром;
- переменные, которые имеют разные значения для клеток, охваченных рассматриваемым контуром склеиваются и не должны входить в конъюнкцию (дизъюнкцию для СКНФ).
Слайд 26Шифратор
Шифратор (кодер) - это устройство, преобразующее m- разрядный позиционный код в
(Или проще - единичный сигнал на одном из входов в n-разрядный двоичный код).
Наибольшее применение он находит в устройствах ввода информации (пультах управления) для преобразования десятичных чисел в двоичную систему счисления.
Слайд 27Шифратор
Предположим, на пульте десять клавиш с гравировкой от 0 до 9.
Как видно из таблицы истинности, в этом случае нужен преобразователь с десятью входами и четырьмя выходами.
Слайд 29Дешифраторы
Дешифратор (декодер) - устройство, преобразующее n – разрядный двоичный код в
(преобразует n - разрядный двоичный код, поступающий на его входы, в сигнал только на одном из его выходов)
Дешифратор двоичного n-разрядного кода имеет 2n выходов, т.к. каждому из 2n значений входного кода должен соответствовать единичный сигнал на одном из выходов дешифратора.
Дешифраторы широко применяются в устройствах управления, для построения распределителей импульсов по различным цепям и т.д
Слайд 32Цифровой мультиплексор
Пропускает(коммутирует) сигнал с одного из входов на один выход в
Слайд 34Сложе́ние по мо́дулю 2 (исключа́ющее «ИЛИ»)
Сумматор по модулю «2» вырабатывает
сигнал логической единицы, если количество его входов с
сигналом логической единицы нечетное.
Слайд 35Одноразрядный двоичный сумматор
PI – перенос из предыдущего разряда
А – бит первого
В- бит второго числа
S - сумма
P0 – перенос в следующий разряд
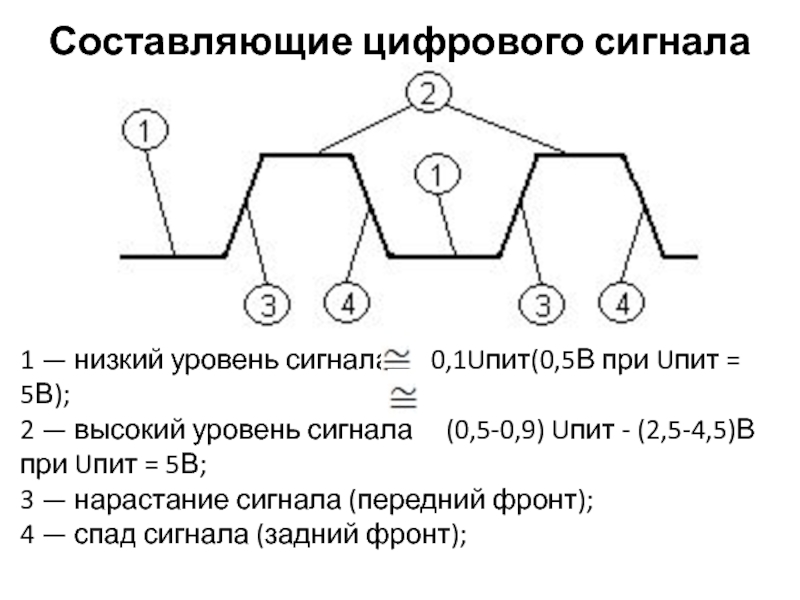
Слайд 38Составляющие цифрового сигнала
1 — низкий уровень сигнала 0,1Uпит(0,5В при
2 — высокий уровень сигнала (0,5-0,9) Uпит - (2,5-4,5)В
при Uпит = 5В;
3 — нарастание сигнала (передний фронт);
4 — спад сигнала (задний фронт);
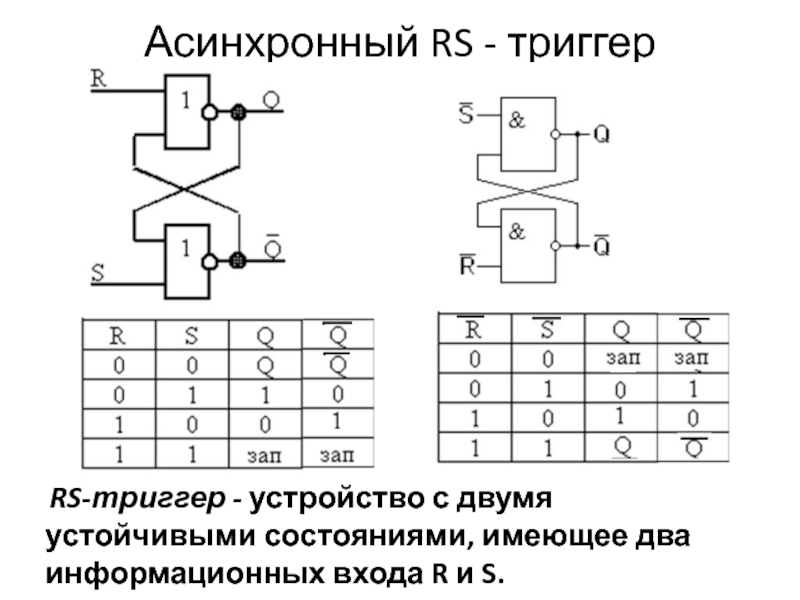
Слайд 39Асинхронный RS - триггер
RS-триггер - устройство с двумя устойчивыми состояниями, имеющее
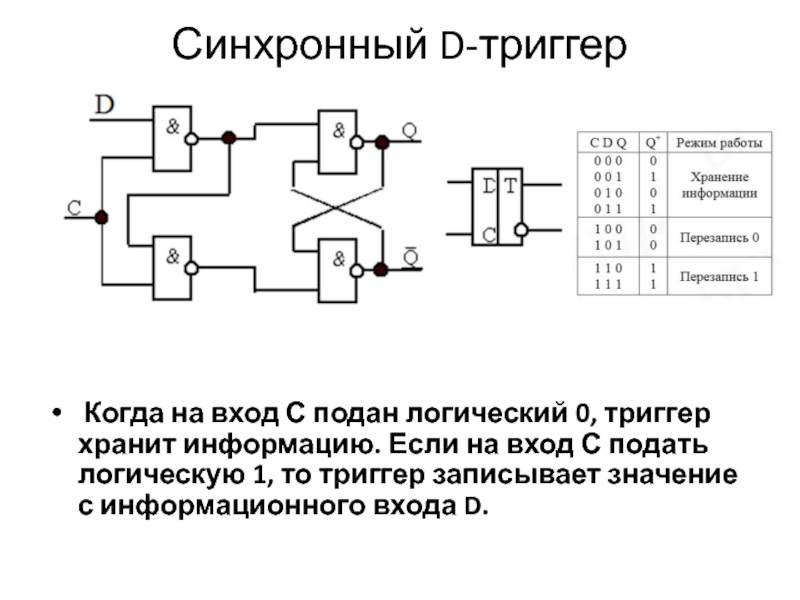
Слайд 40Синхронный D-триггер
Когда на вход С подан логический 0, триггер хранит информацию.
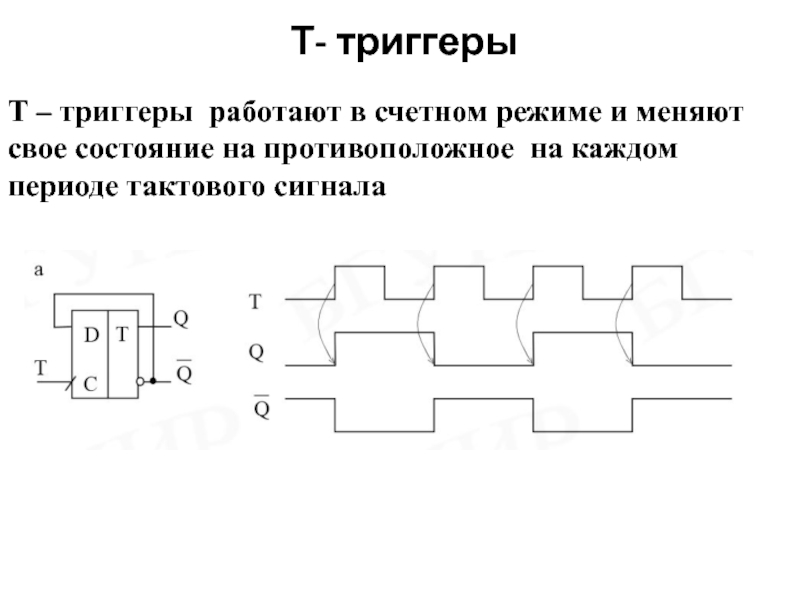
Слайд 41 Т- триггеры
Т – триггеры работают в счетном режиме и меняют
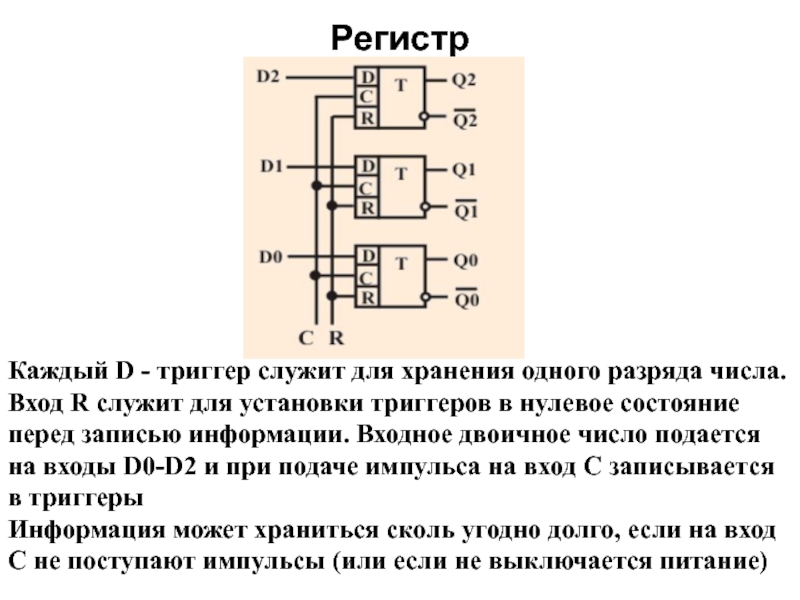
Слайд 42Регистр
Каждый D - триггер служит для хранения одного разряда числа. Вход
Информация может храниться сколь угодно долго, если на вход С не поступают импульсы (или если не выключается питание)
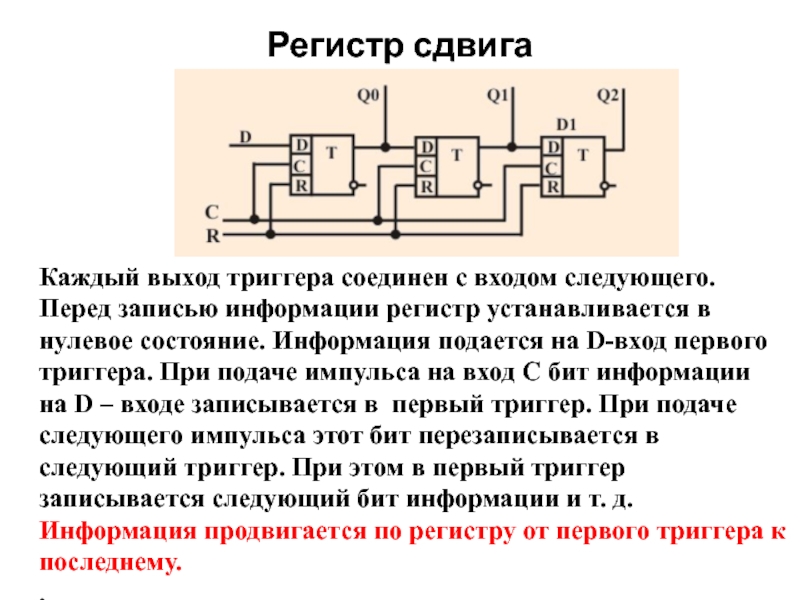
Слайд 43Регистр сдвига
Каждый выход триггера соединен с входом следующего.
Перед записью информации регистр
.
Слайд 44Цифровой счетчик
Цифровой счетчик импульсов - это цифровой узел, который осуществляет счет
N = 2n - 1, где n - число триггеров,