- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Аналіз систем, які працюють за дисципліною обслуговування з очікуванням презентация
Содержание
- 1. Аналіз систем, які працюють за дисципліною обслуговування з очікуванням
- 2. Основні питання Визначення ймовірностей станів СРІ
- 3. Постановка задачі Вважається, що повністю доступна
- 4. Визначення ймовірностей станів СРІ
- 5. Визначення ймовірностей станів СРІ Отримаємо вирази для
- 6. Друга формула Ерланга Дану
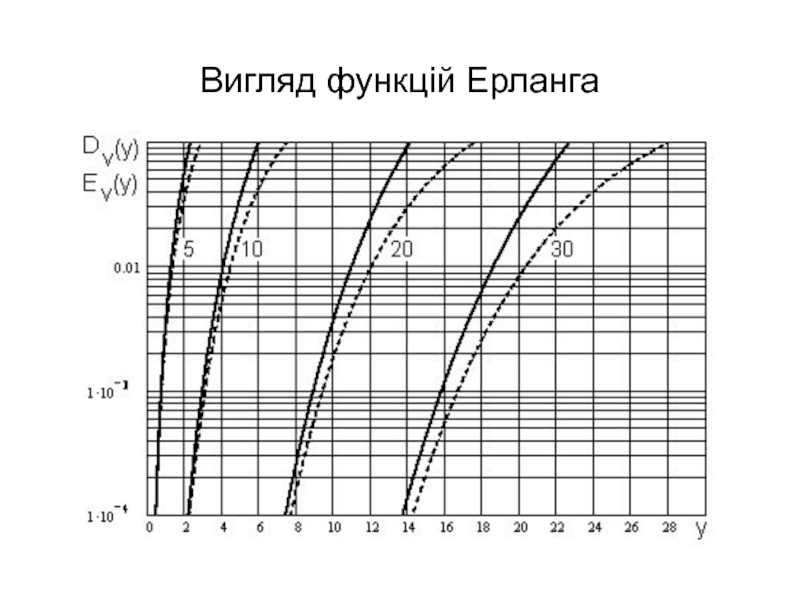
- 7. Вигляд функцій Ерланга
- 8. Розподіл часу очікування у випадку дисципліни черги
- 9. Формула Літтла Формула Літтла встановлює
- 10. Доведення формули Літтла Рассмотрим любую СМО (одноканальную,
- 11. Доведення формули Літтла Обозначим: -
- 12. Доведення формули Літтла Вид функций α(t) и
- 13. Доведення формули Літтла Очевидно, что для любого
- 14. Доведення формули Літтла Рассмотрим очень большой промежуток
- 15. Доведення формули Літтла Но этот интеграл представляет
- 16. Доведення формули Літтла Обозначим эти времена t1,
- 17. Доведення формули Літтла Разделим правую и левую
- 18. Доведення формули Літтла Но величина Tλ есть
- 19. Доведення формули Літтла Это и есть формула
- 20. Друга формула Літтла Точно таким же образом
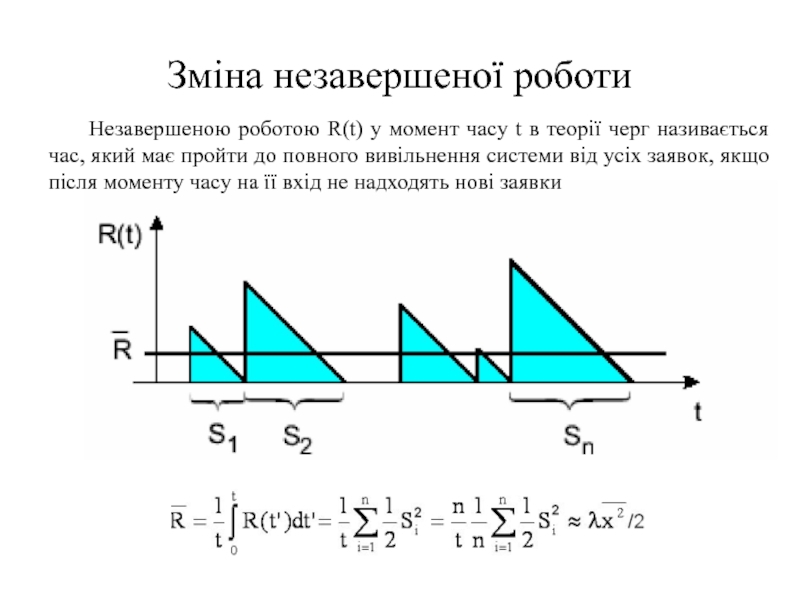
- 21. Зміна незавершеної роботи Незавершеною роботою R(t) у
- 22. Аналіз системи M/G/1 Вхідний потік:
- 23. Формула Полячека-Хінчина
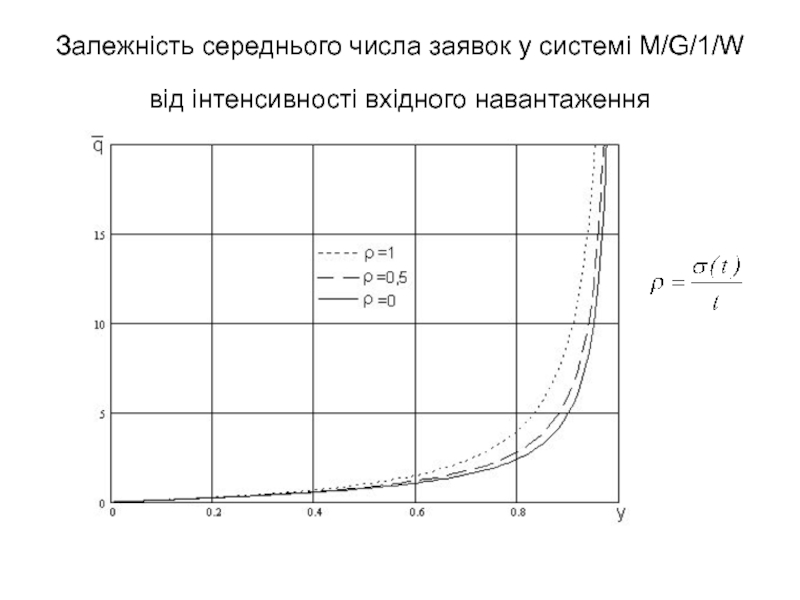
- 24. Залежність середнього числа заявок у системі M/G/1/W від інтенсивності вхідного навантаження
- 25. Система M/D/v/W Постановка задачі у даному
- 26. Система M/D/v/W
- 27. Система M/D/v/W
- 28. Система M/D/v/W
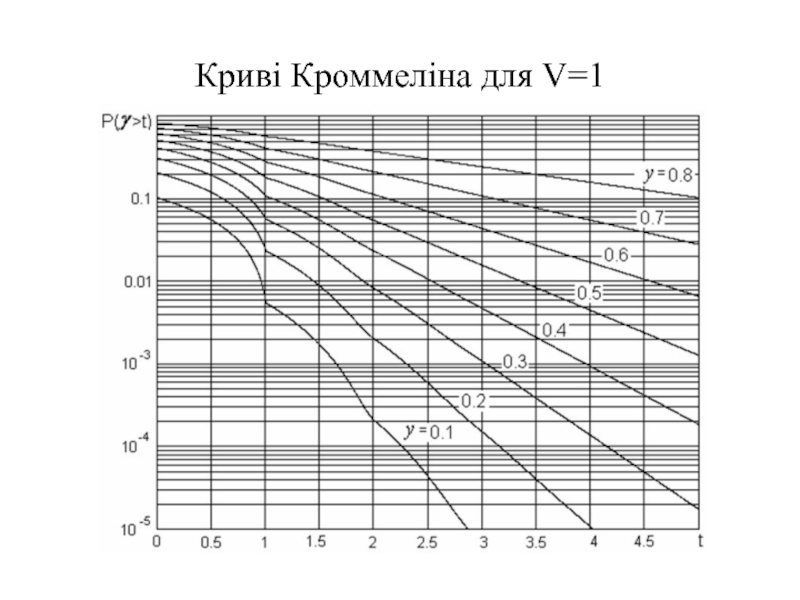
- 29. Криві Кроммеліна для V=1
- 30. Дисципліни вибору з черги Практичний інтерес
- 31. Дисципліни вибору з черги
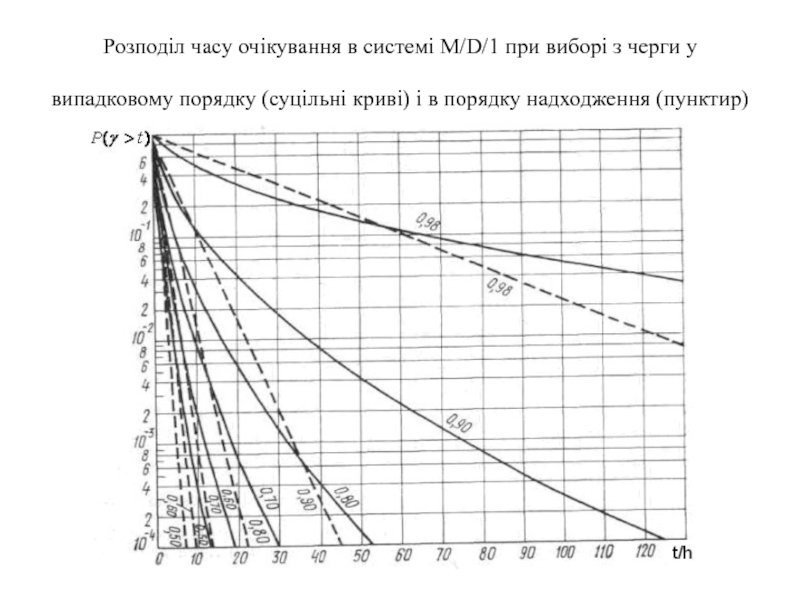
- 32. Розподіл часу очікування в системі M/D/1 при
Слайд 1Лекція 7
Аналіз систем, які працюють за дисципліною обслуговування з очікуванням
Література
1. Омельченко
Слайд 2Основні питання
Визначення ймовірностей станів СРІ
Розподіл часу очікування у випадку дисципліни
Формула Літтла
Формула Полячека-Хінчина
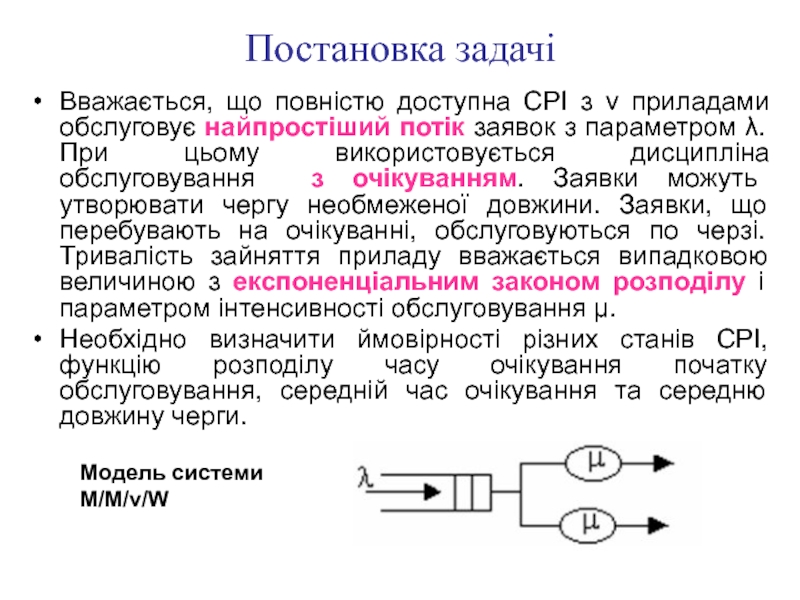
Слайд 3Постановка задачі
Вважається, що повністю доступна СРІ з v приладами обслуговує
Необхідно визначити ймовірності різних станів СРІ, функцію розподілу часу очікування початку обслуговування, середній час очікування та середню довжину черги.
Модель системи
M/M/v/W
Слайд 5Визначення ймовірностей станів СРІ
Отримаємо вирази для станів СРІ типу M/M/v/W
Рекурентні співвідношення
Слайд 6Друга формула Ерланга
Дану формулу часто називають
С-формулою Ерланга.
Agner Krarup Erlang
Слайд 8Розподіл часу очікування у випадку дисципліни черги FIFO
У даному випадку
=
.
,
,
,
,
.
Слайд 9Формула Літтла
Формула Літтла встановлює співвідношення між середнім числом викликів в
Останнє співвідношення означає, що середнє число заявок у системі дорівнює добутку інтенсивності надходження заявок у систему на середній час їхнього перебування в системі:
При цьому не накладається жодних обмежень на тип потоку заявок і час обслуговування. Вперше доведення цього факту дав Дж. Літтл.
Слайд 10Доведення формули Літтла
Рассмотрим любую СМО (одноканальную, многоканальную, марковскую, немарковскую, с неограниченной
- поток заявок, прибывающих в СМО;
- поток заявок, покидающих СМО.
Если в системе установился предельный, стационарный режим, то среднее число заявок, прибывающих в СМО за единицу времени, равно среднему числу заявок, покидающих её.
Оба потока имеют одну и ту же интенсивность λ.
Слайд 11Доведення формули Літтла
Обозначим:
- α(t) – число заявок, прибывших в
- δ(t) - число заявок, покинувших СМО до момента t.
И та и другая функции являются случайными и меняются скачком (увеличиваются на единицу) в моменты приходов заявок α(t) и уходов заявок δ(t).
Слайд 12Доведення формули Літтла
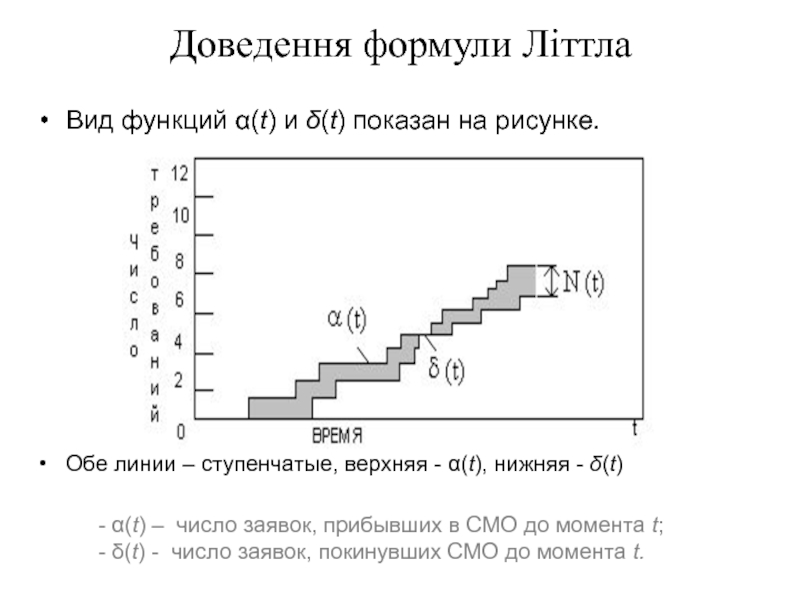
Вид функций α(t) и δ(t) показан на рисунке.
Обе линии
- α(t) – число заявок, прибывших в СМО до момента t;
- δ(t) - число заявок, покинувших СМО до момента t.
Слайд 13Доведення формули Літтла
Очевидно, что для любого момента t их разность N(t)
Когда линии α(t) и δ(t) сливаются, в системе нет заявок
Слайд 14Доведення формули Літтла
Рассмотрим очень большой промежуток времени T (мысленно продолжив график
Оно будет равно интегралу от функции N(t) на этом промежутке, деленному на длину интервала T:
Слайд 15Доведення формули Літтла
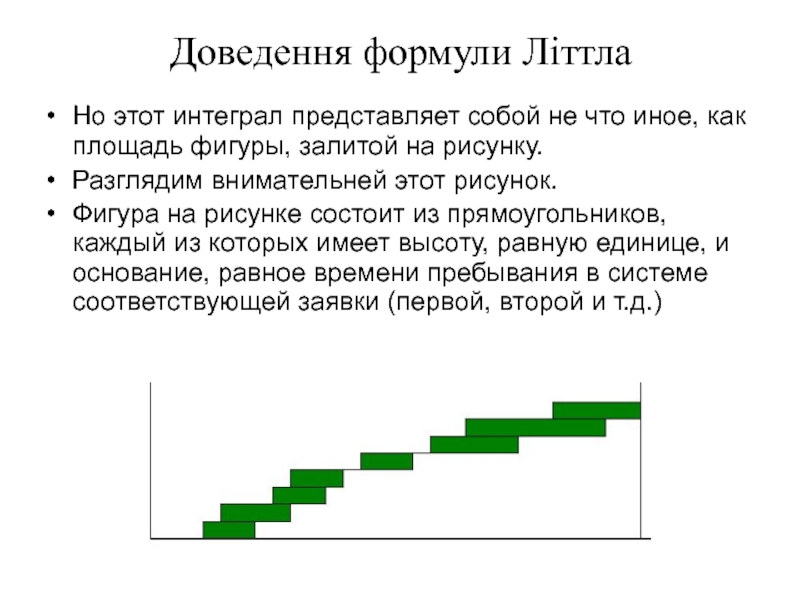
Но этот интеграл представляет собой не что иное, как
Разглядим внимательней этот рисунок.
Фигура на рисунке состоит из прямоугольников, каждый из которых имеет высоту, равную единице, и основание, равное времени пребывания в системе соответствующей заявки (первой, второй и т.д.)
Слайд 16Доведення формули Літтла
Обозначим эти времена t1, t2,…
Правда, под конец промежутка T
Таким образом, можно считать, что:
где сумма распространяется на все заявки, пришедшие за время T
Слайд 17Доведення формули Літтла
Разделим правую и левую часть последнего выражения на длину
Получим
Разделим и умножим правую часть на интенсивность λ:
Слайд 18Доведення формули Літтла
Но величина Tλ есть не что иное, как среднее
Если мы разделим сумму всех времен ti на среднее число заявок, то получим среднее время пребывания заявки в системе
Итак:
откуда:
Слайд 19Доведення формули Літтла
Это и есть формула Литтла:
- для любой
Слайд 20Друга формула Літтла
Точно таким же образом выводится вторая формула Литтла, связывающая
Слайд 21Зміна незавершеної роботи
Незавершеною роботою R(t) у момент часу t в теорії
Слайд 22Аналіз системи M/G/1
Вхідний потік:
Час обслуговування:
Інтенсивність навантаження:
Середній час очікування:
Середнє число заявок у черзі:
где - середня незавершена робота
,
Слайд 23Формула Полячека-Хінчина
(Формула ПХ)
Наслідок 1.
Наслідок 2.
Наслідок 3. Для моделі M/М/1
Наслідок 4. Для моделі M/D/1
Середній час очікування початку обслуговування
Слайд 24Залежність середнього числа заявок у системі M/G/1/W від інтенсивності вхідного навантаження
Слайд 25Система M/D/v/W
Постановка задачі у даному випадку така сама, як для
Відмінність полягає лише в законі розподілу тривалості обслуговування: замість випадкового закону розподілу тривалість обслуговування кожної заявки вважається постійною величиною, рівною h. Цей випадок вперше у 1932 р. дослідив Кроммелін.
Розглянемо підхід, що використовується у теорії Кроммеліна.
Без обмеження загальності припустимо, що h=1.