- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Алгоритмизация и программирование. Язык C++. (§ 38 - § 45) презентация
Содержание
- 1. Алгоритмизация и программирование. Язык C++. (§ 38 - § 45)
- 2. Алгоритмизация и программирование. Язык C++ § 38. Целочисленные алгоритмы
- 3. Решето Эратосфена Эратосфен Киренский (Eratosthenes, Ερατοσθδνη) (ок.
- 4. Решето Эратосфена Задача. Вывести все простые числа
- 5. Решето Эратосфена Вычёркивание непростых: k = 2; while ( k*k
- 6. Решето Эратосфена Вывод результата: for ( i = 2; i
- 7. «Длинные» числа Ключи для шифрования: ≥ 256
- 8. «Длинные» числа A = 12345678 нужно хранить
- 9. «Длинные» числа Упаковка элементов: 12345678 = 12·10002
- 10. Вычисление факториала Задача 1. Вычислить точно значение
- 11. Вычисление факториала основание d = 1 000 000 [A]
- 12. Вычисление факториала r = 0; for ( i = 0; i
- 13. Вывод длинного числа [A] = 1000002000003 найти
- 14. Вывод длинного числа for ( k =
- 15. Вывод длинного числа Вывод числа с лидирующими
- 16. Конец фильма ПОЛЯКОВ Константин Юрьевич д.т.н., учитель
- 17. Источники иллюстраций wallpaperscraft.com www.mujerhoy.com www.pinterest.com www.wayfair.com www.zchocolat.com
Слайд 1Алгоритмизация и программирование. Язык C++
§ 38. Целочисленные алгоритмы
§ 39. Структуры
§ 40.
§ 41. Списки
§ 42. Стек, очередь, дек
§ 43. Деревья
§ 44. Графы
§ 45. Динамическое программирование
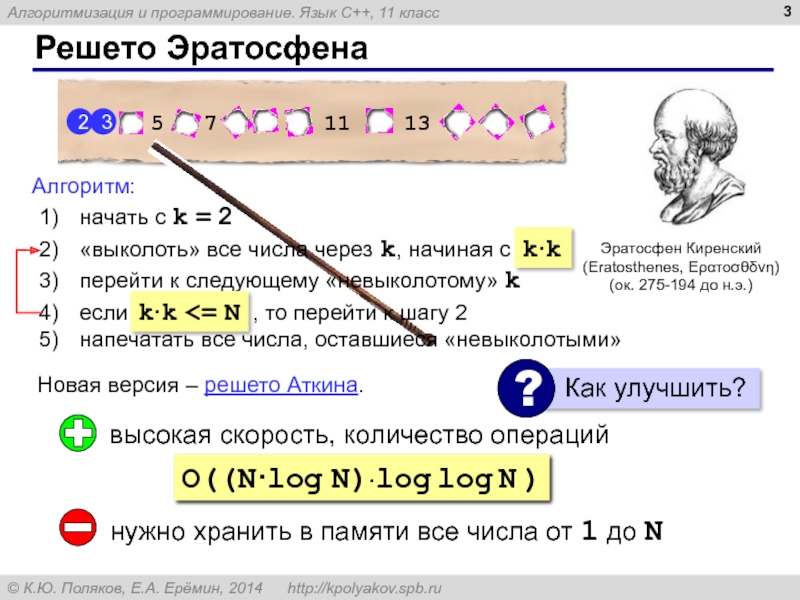
Слайд 3Решето Эратосфена
Эратосфен Киренский
(Eratosthenes, Ερατοσθδνη)
(ок. 275-194 до н.э.)
Новая версия – решето
2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
Алгоритм:
начать с k = 2
«выколоть» все числа через k, начиная с 2·k
перейти к следующему «невыколотому» k
если k <= N , то перейти к шагу 2
напечатать все числа, оставшиеся «невыколотыми»
высокая скорость, количество операций
нужно хранить в памяти все числа от 1 до N
O((N·log N)·log log N )
2
3
k·k
k·k <= N
Слайд 4Решето Эратосфена
Задача. Вывести все простые числа от 2 до N.
Объявление переменных:
const
bool A[N+1];
int i, k;
Сначала все невычеркнуты:
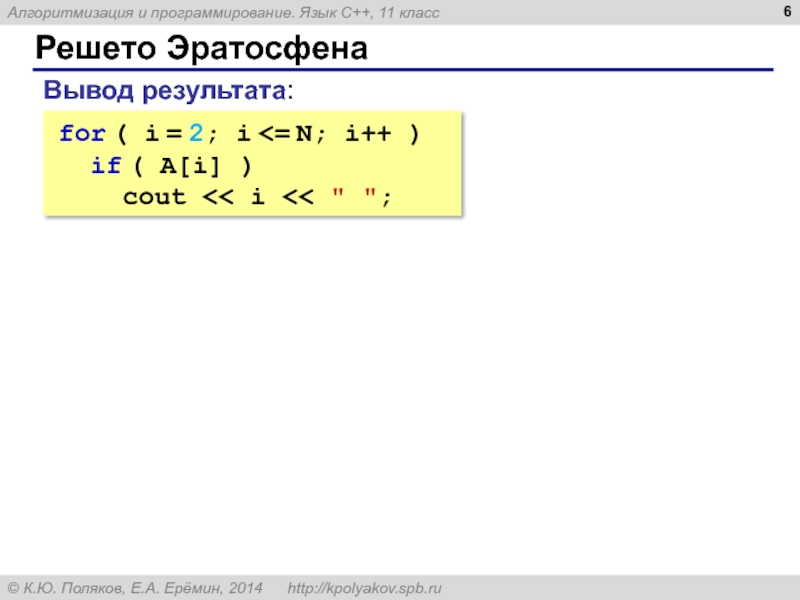
for ( i = 2; i <= N; i++ )
A[i] = true;
выделяем на 1 элемент больше, чтобы начать с A[1]
Слайд 5Решето Эратосфена
Вычёркивание непростых:
k = 2;
while ( k*k
i = k*k;
while ( i <= N )
{
A[i] = false;
i += k;
}
}
k ++;
}
Слайд 7«Длинные» числа
Ключи для шифрования: ≥ 256 битов.
Целочисленные типы данных: ≤ 64
Длинное число – это число, которое не помещается в переменную одного из стандартных типов данных языка программирования.
«Длинная арифметика» – алгоритмы для работы с длинными числами.
Слайд 8«Длинные» числа
A = 12345678
нужно хранить длину числа
неудобно вычислять (с младшего разряда!)
неэкономное
Обратный порядок элементов:
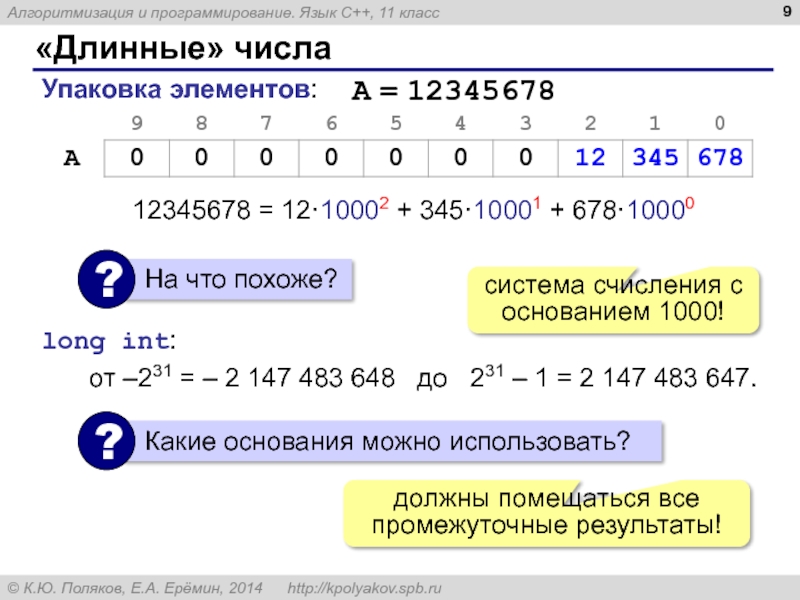
Слайд 9«Длинные» числа
Упаковка элементов:
12345678 = 12·10002 + 345·10001 + 678·10000
система счисления с
от –231 = – 2 147 483 648 до 231 – 1 = 2 147 483 647.
long int:
должны помещаться все промежуточные результаты!
A = 12345678
Слайд 10Вычисление факториала
Задача 1. Вычислить точно значение факториала
100! = 1·2·3·…·99·100
1·2·3·…·99·100
201 цифра
6 цифр в ячейке ⇒ 34 ячейки
const int N = 33;
long int A[N+1];
Основной алгоритм:
[A] = 1;
for ( k = 2; k <= 100; k ++ )
[A] = [A] * k;
длинное число
основание 1000000
Слайд 11
Вычисление факториала
основание d = 1 000 000
[A] = 12345678901734567
734 567·3 = 2 203 701
*3
остаётся
r = перенос в A[1]
s = A[0]*k;
A[0] = s % d;
r = s / d;
s = A[1]*k + r;
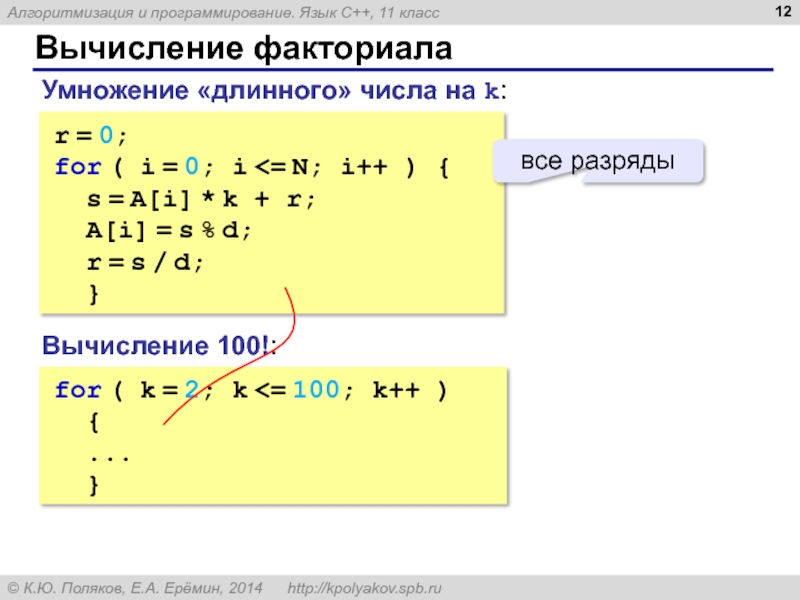
Слайд 12Вычисление факториала
r = 0;
for ( i = 0; i
s = A[i] * k + r;
A[i] = s % d;
r = s / d;
}
Умножение «длинного» числа на k:
Вычисление 100!:
for ( k = 2; k <= 100; k++ )
{
...
}
все разряды
Слайд 13Вывод длинного числа
[A] = 1000002000003
найти старший ненулевой разряд
вывести этот разряд
вывести все
i = N;
while ( ! A[i] )
i --;
cout << A[i];
Слайд 14Вывод длинного числа
for ( k = i-1; k >= 0; k--
Write6 ( A[k] );
Вывод остальных разрядов:
со старшего
Write6:
x = 12345
012345
x / 100000
x % 100000
Слайд 15Вывод длинного числа
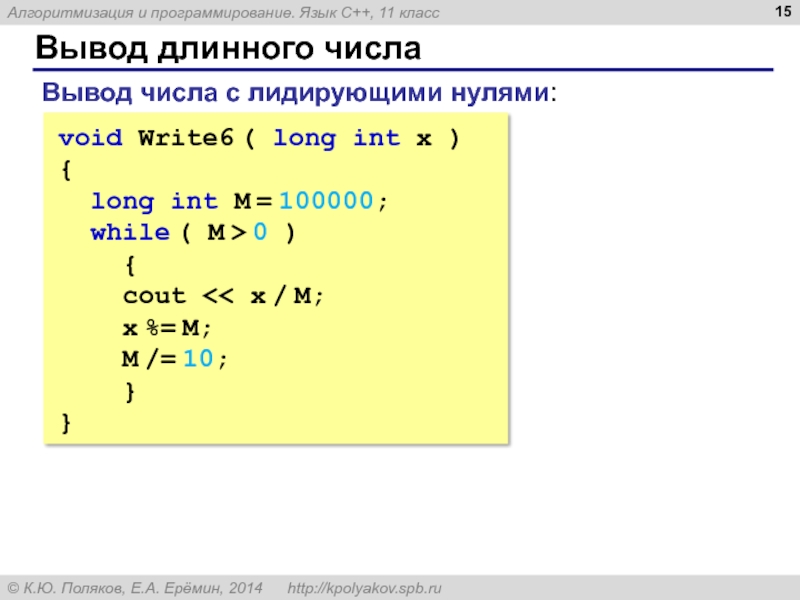
Вывод числа с лидирующими нулями:
void Write6 ( long int
{
long int M = 100000;
while ( M > 0 )
{
cout << x / M;
x %= M;
M /= 10;
}
}
Слайд 16Конец фильма
ПОЛЯКОВ Константин Юрьевич
д.т.н., учитель информатики
ГБОУ СОШ № 163, г. Санкт-Петербург
kpolyakov@mail.ru
к.ф.-м.н., доцент кафедры мультимедийной дидактики и ИТО ПГГПУ, г. Пермь
eremin@pspu.ac.ru







![Вычисление факториалаоснование d = 1 000 000[A] = 12345678901734567 734 567·3 = 2 203 701*3остаётся в A[0]r = перенос](/img/tmb/5/460508/fbeae87fa742d686a5d22bf853f31aec-800x.jpg)
![Вывод длинного числа[A] = 1000002000003найти старший ненулевой разрядвывести этот разрядвывести все следующие разряды, добавляя лидирующие](/img/tmb/5/460508/5cab56aa38d66e64b706d60810bd1f31-800x.jpg)
![Вывод длинного числаfor ( k = i-1; k >= 0; k-- ) Write6 ( A[k]](/img/tmb/5/460508/1c977068809b9f24b92e1a7fdd8242cc-800x.jpg)