- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Алгебра высказываний презентация
Содержание
- 1. Алгебра высказываний
- 2. В алгебре высказываний суждениям (простым высказываниям) ставятся
- 3. ЛОГИЧЕСКОЕ УМНОЖЕНИЕ (конъюнкция) Составное высказывание, образованное в
- 4. ЛОГИЧЕСКОЕ УМНОЖЕНИЕ (конъюнкция) В естественном языке –
- 5. ЛОГИЧЕСКОЕ УМНОЖЕНИЕ (конъюнкция)
- 6. ЛОГИЧЕСКОЕ СЛОЖЕНИЕ (дизъюнкция) Составное высказывание, образованное
- 7. ЛОГИЧЕСКОЕ СЛОЖЕНИЕ (дизъюнкция) В естественном языке –
- 8. ЛОГИЧЕСКОЕ СЛОЖЕНИЕ (дизъюнкция)
- 9. ЛОГИЧЕСКОЕ ОТРИЦАНИЕ (инверсия) Отрицание – это
- 10. ЛОГИЧЕСКОЕ ОТРИЦАНИЕ (инверсия) В естественном языке: «Неверно,
- 11. ЛОГИЧЕСКОЕ ОТРИЦАНИЕ (инверсия)
- 12. ЛОГИЧЕСКОЕ СЛЕДОВАНИЕ (импликация) Импликация – это логическая
- 13. ЛОГИЧЕСКОЕ СЛЕДОВАНИЕ (импликация) В естественном языке: «Если
- 14. ЛОГИЧЕСКОЕ СЛЕДОВАНИЕ (импликация)
- 15. ЛОГИЧЕСКАЯ РАВНОЗНАЧНОСТЬ (эквиваленция/ эквивалентность) Логическая равнозначность
- 16. ЛОГИЧЕСКАЯ РАВНОЗНАЧНОСТЬ (эквиваленция) В естественном языке: «Тогда
- 17. ЛОГИЧЕСКАЯ РАВНОЗНАЧНОСТЬ (эквиваленция)
- 18. КОНТРОЛЬНЫЕ ВОПРОСЫ
- 19. Чем заменяются высказывания в алгебре высказываний? Какие
- 20. ЗАДАНИЯ ДЛЯ САМОСТОЯТЕЛЬНОГО ВЫПОЛНЕНИЯ
- 21. Постройте таблицу истинности операции логического умножения. Составьте
- 22. 5. Даны два высказывания: А={2x2=4}, B={2x2=5}. Они
- 23. Спасибо за внимание
Слайд 2В алгебре высказываний суждениям (простым высказываниям) ставятся в соответствие логические переменные
(заглавные буквы латинского алфавита).
Для образования новых высказываний наиболее часто используются базовые логические операции, выражаемые словами «И», «ИЛИ», «НЕТ».
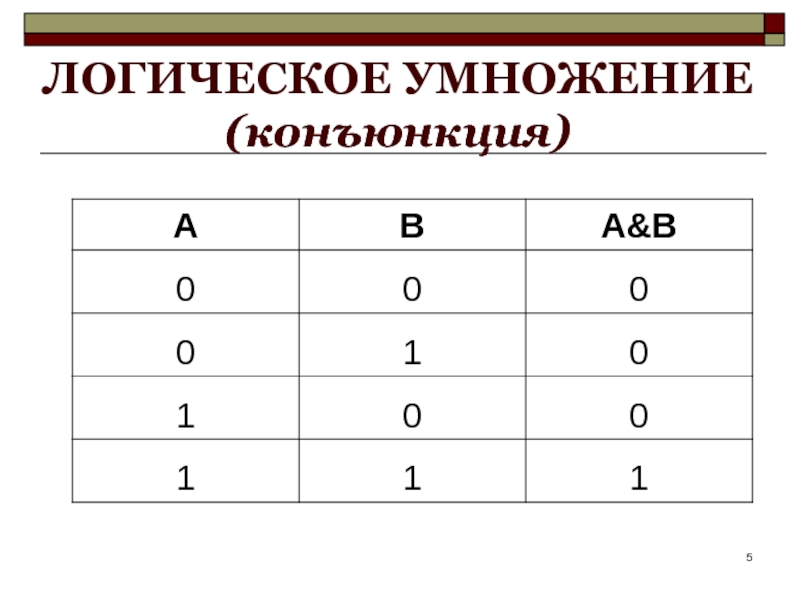
Слайд 3ЛОГИЧЕСКОЕ УМНОЖЕНИЕ
(конъюнкция)
Составное высказывание, образованное в результате операции логического умножения (конъюнкции), истинно
тогда и только тогда, когда истинны входящие в него простые высказывания
Слайд 4ЛОГИЧЕСКОЕ УМНОЖЕНИЕ
(конъюнкция)
В естественном языке – И;
Обозначение - &;
В языке программирования –
and;
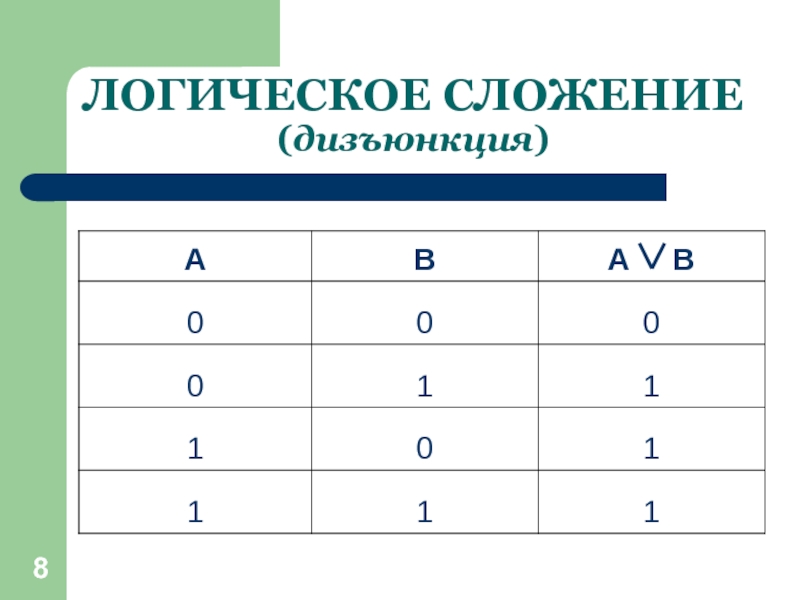
Слайд 6ЛОГИЧЕСКОЕ СЛОЖЕНИЕ (дизъюнкция)
Составное высказывание, образованное в результате логического сложения (дизъюнкции),
истинно тогда и только тогда, когда истинно хотя бы одно из входящих в него простых высказываний
Слайд 7ЛОГИЧЕСКОЕ СЛОЖЕНИЕ (дизъюнкция)
В естественном языке – ИЛИ;
Обозначение -
В языке программирования
– or;
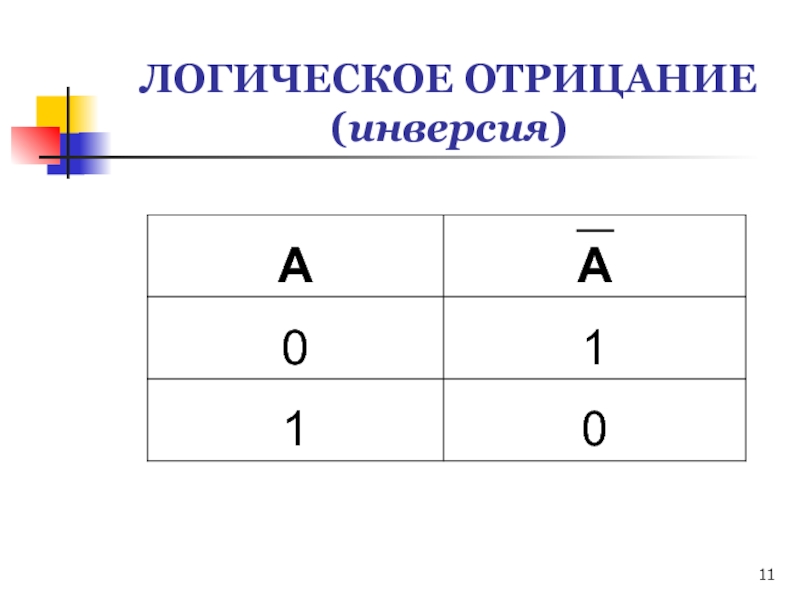
Слайд 9ЛОГИЧЕСКОЕ ОТРИЦАНИЕ (инверсия)
Отрицание – это логическая операция, которая каждому простому
высказыванию ставит в соответствие составное высказывание, заключающееся в том, что исходное высказывание отрицаемо.
Логическое отрицание (инверсия) делает истинное высказывание ложным и, наоборот, ложное – истинным.
Логическое отрицание (инверсия) делает истинное высказывание ложным и, наоборот, ложное – истинным.
Слайд 10ЛОГИЧЕСКОЕ ОТРИЦАНИЕ (инверсия)
В естественном языке: «Неверно,
что …» или
частичка не;
Обозначение: A ;
В языке программирования: not;
Обозначение: A ;
В языке программирования: not;
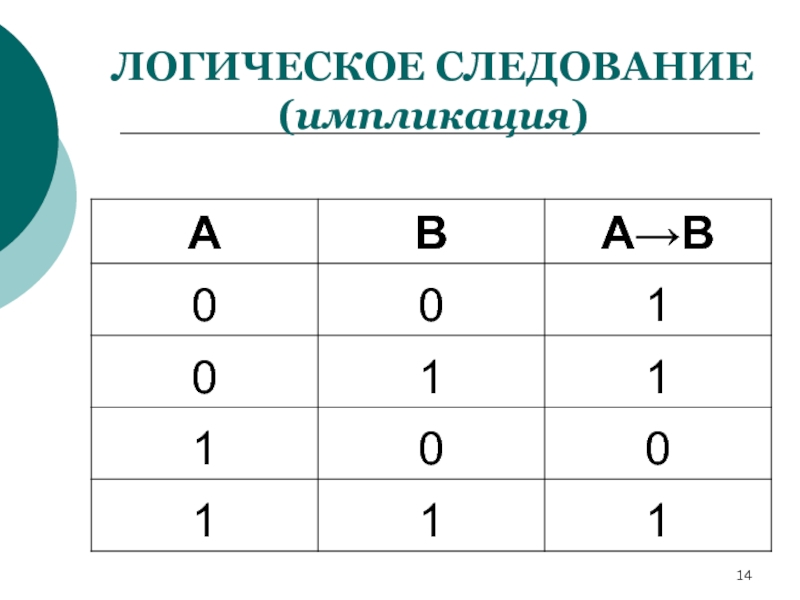
Слайд 12ЛОГИЧЕСКОЕ СЛЕДОВАНИЕ (импликация)
Импликация – это логическая операция, ставящая в соответствие каждым
двум простым высказываниям составное высказывание, являющееся ложным тогда и только тогда, когда условие (первое высказывание) истинно, а следствие (второе высказывание) ложно.
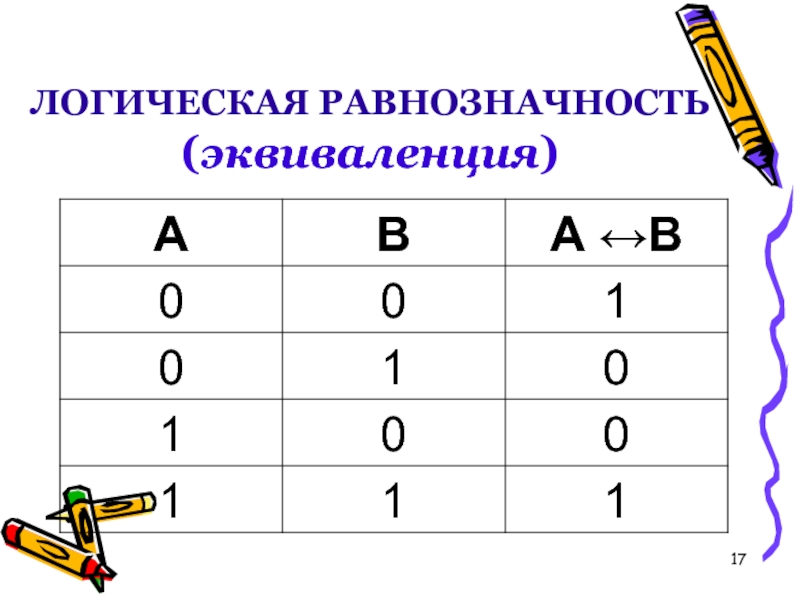
Слайд 15ЛОГИЧЕСКАЯ РАВНОЗНАЧНОСТЬ (эквиваленция/
эквивалентность)
Логическая равнозначность – это логическая операция, ставящая в
соответствие каждым двум высказываниям составное высказывание, являющееся истинным тогда и только тогда, когда оба исходных высказывания одновременно истины или одновременно ложны.
Слайд 16ЛОГИЧЕСКАЯ РАВНОЗНАЧНОСТЬ (эквиваленция)
В естественном языке: «Тогда и только тогда» или «В
том и только том случае»;
Обозначение: ↔ .
Обозначение: ↔ .
Слайд 19Чем заменяются высказывания в алгебре высказываний?
Какие значения могут принимать логические переменные?
Какие
существуют базовые логические операции и какими символами они обозначаются?
Слайд 21Постройте таблицу истинности операции логического умножения. Составьте составное высказывание, содержащее данную
операцию.
Постройте таблицу истинности операции логического сложения. Составьте составное высказывание, содержащее данную операцию.
Постройте таблицу истинности операции логического отрицания. Составьте составное высказывание, содержащее данную операцию.
Простое высказывание А истинно, а высказывание В – ложно. Что можно сказать об истинности составного высказывания, которое объединяет эти простые операцией логического умножения? Логического сложения?
Постройте таблицу истинности операции логического сложения. Составьте составное высказывание, содержащее данную операцию.
Постройте таблицу истинности операции логического отрицания. Составьте составное высказывание, содержащее данную операцию.
Простое высказывание А истинно, а высказывание В – ложно. Что можно сказать об истинности составного высказывания, которое объединяет эти простые операцией логического умножения? Логического сложения?
Слайд 225. Даны два высказывания:
А={2x2=4}, B={2x2=5}. Они истинны или ложны?
Какие из следующих
высказываний истинны?
а)А; б)В; в)А&В; г)А В; д)А→В;
е)А ↔ В.
6. Даны простые высказывания:
А={5>3} , B={2=3}, C={4<2}.
Определите истинность составного высказывания: (А&В) С ↔(А С)&(А&B)
а)А; б)В; в)А&В; г)А В; д)А→В;
е)А ↔ В.
6. Даны простые высказывания:
А={5>3} , B={2=3}, C={4<2}.
Определите истинность составного высказывания: (А&В) С ↔(А С)&(А&B)