- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Адаптивная фильтрация презентация
Содержание
- 1. Адаптивная фильтрация
- 2. ОСНОВНЫЕ ОБЛАСТИ ПРИМЕНЕНИЯ АДАПТИВНЫЕ ФИЛЬТРЫ –
- 3. НАИБОЛЕЕ РАСПРОСТРАНЕННЫЕ СХЕМЫ АДАПТИВНОЙ ФИЛЬТРАЦИИ СИГНАЛОВ АДАПТИВНЫЙ
- 4. АДАПТИВНЫЙ ШУМОПОДАВИТЕЛЬ ПОЛЕЗНЫЙ СИГНАЛ ОЦЕНИВАЕТСЯ ПО РАЗНОСТИ:
- 5. АДАПТИВНЫЙ ФИЛЬТР ВИНЕРА ФИЛЬТР ФОРМИРУЕТ ИЗ X(К)
- 6. В СТАЦИОНАРНОЙ СРЕДЕ ГРАФИК ЗАВИСИМОСТИ E ОТ
- 7. АДАПТИВНЫЙ АЛГОРИТМ НАИМЕНЬШИХ КВАДРАТОВ УИДРОУ-ХОПФА ПО СУЩЕСТВУ,
- 8. РЕКУРСИВНЫЕ СХЕМЫ НАИМЕНЬШИХ КВАДРАТОВ ОТЛИЧАЕТСЯ ТЕМ, ЧТО
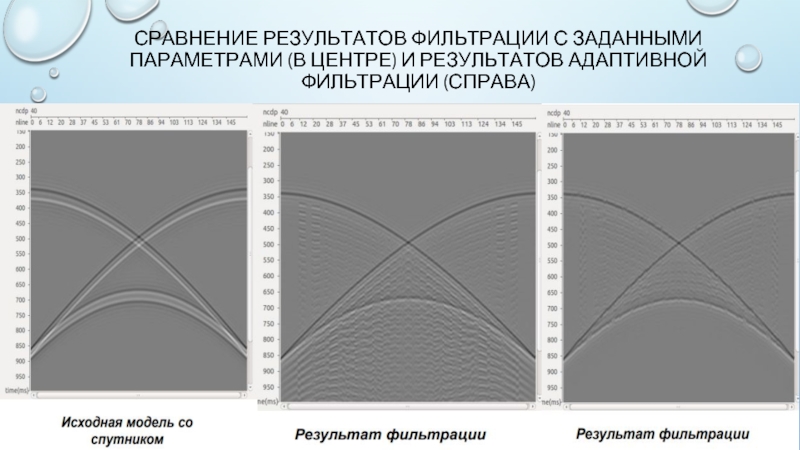
- 9. СРАВНЕНИЕ РЕЗУЛЬТАТОВ ФИЛЬТРАЦИИ С ЗАДАННЫМИ ПАРАМЕТРАМИ (В ЦЕНТРЕ) И РЕЗУЛЬТАТОВ АДАПТИВНОЙ ФИЛЬТРАЦИИ (СПРАВА)
- 10. СРАВНЕНИЕ РЕЗУЛЬТАТОВ ФИЛЬТРАЦИИ В КОНФЛИКТНОЙ ЗОНЕ
- 11. ИТОГИ: НАИБОЛЕЕ ВАЖНОЙ ЧАСТЬЮ АДАПТИВНОГО КОМПЕНСАТОРА ПОМЕХ
- 12. СПИСОК ЛИТЕРАТУРЫ А.В. ДАВЫДОВ «ЦИФРОВАЯ ОБРАБОТКА СИГНАЛОВ»,
- 13. ВОПРОСЫ К ЗАЧЁТУ ТРИ ОСНОВНЫЕ ПРИЧИНЫ ПРИМЕНЕНИЯ
Слайд 2ОСНОВНЫЕ ОБЛАСТИ ПРИМЕНЕНИЯ
АДАПТИВНЫЕ ФИЛЬТРЫ – ЭТО ЦИФРОВЫЕ ФИЛЬТРЫ, КОТОРЫЕ СПОСОБНЫ
ОЧИСТКА ДАННЫХ ОТ НЕСТАБИЛЬНЫХ МЕШАЮЩИХ СИГНАЛОВ И ШУМОВ
ПРИЧИНЫ:
ПОЛОСА ЧАСТОТ ШУМА НЕИЗВЕСТНА ИЛИ ИЗМЕНЯЕТСЯ СО ВРЕМЕНЕМ,
СПЕКТРЫ ПОЛЕЗНОГО СИГНАЛА И ШУМА (ПОМЕХИ) ПЕРЕКРЫВАЮТСЯ,
ХАРАКТЕРИСТИКИ ПОЛЕЗНОГО СИГНАЛА И ШУМОВ, КАНАЛОВ ПЕРЕДАЧИ ЯВЛЯЮТСЯ НЕСТАЦИОНАРНЫМИ.
Слайд 3НАИБОЛЕЕ РАСПРОСТРАНЕННЫЕ СХЕМЫ АДАПТИВНОЙ ФИЛЬТРАЦИИ СИГНАЛОВ
АДАПТИВНЫЙ ШУМОПОДАВИТЕЛЬ
АДАПТИВНЫЙ ФИЛЬТР ВИНЕРА
АДАПТИВНЫЙ АЛГОРИТМ НАИМЕНЬШИХ
РЕКУРСИВНЫЕ СХЕМЫ НАИМЕНЬШИХ КВАДРАТОВ
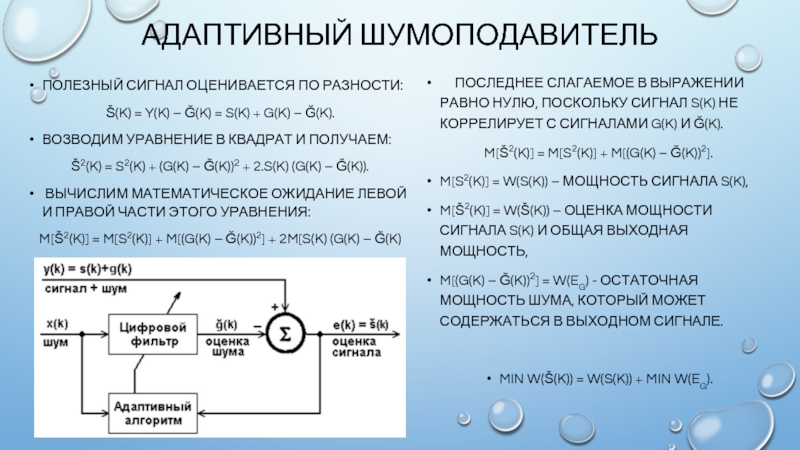
Слайд 4АДАПТИВНЫЙ ШУМОПОДАВИТЕЛЬ
ПОЛЕЗНЫЙ СИГНАЛ ОЦЕНИВАЕТСЯ ПО РАЗНОСТИ:
Š(K) = Y(K) – Ğ(K) =
ВОЗВОДИМ УРАВНЕНИЕ В КВАДРАТ И ПОЛУЧАЕМ:
Š2(K) = S2(K) + (G(K) – Ğ(K))2 + 2.S(K) (G(K) – Ğ(K)).
ВЫЧИСЛИМ МАТЕМАТИЧЕСКОЕ ОЖИДАНИЕ ЛЕВОЙ И ПРАВОЙ ЧАСТИ ЭТОГО УРАВНЕНИЯ:
M[Š2(K)] = M[S2(K)] + M[(G(K) – Ğ(K))2] + 2M[S(K) (G(K) – Ğ(K)
ПОСЛЕДНЕЕ СЛАГАЕМОЕ В ВЫРАЖЕНИИ РАВНО НУЛЮ, ПОСКОЛЬКУ СИГНАЛ S(K) НЕ КОРРЕЛИРУЕТ С СИГНАЛАМИ G(K) И Ğ(K).
M[Š2(K)] = M[S2(K)] + M[(G(K) – Ğ(K))2].
M[S2(K)] = W(S(K)) – МОЩНОСТЬ СИГНАЛА S(K),
M[Š2(K)] = W(Š(K)) – ОЦЕНКА МОЩНОСТИ СИГНАЛА S(K) И ОБЩАЯ ВЫХОДНАЯ МОЩНОСТЬ,
M[(G(K) – Ğ(K))2] = W(EG) - ОСТАТОЧНАЯ МОЩНОСТЬ ШУМА, КОТОРЫЙ МОЖЕТ СОДЕРЖАТЬСЯ В ВЫХОДНОМ СИГНАЛЕ.
MIN W(Š(K)) = W(S(K)) + MIN W(EG).
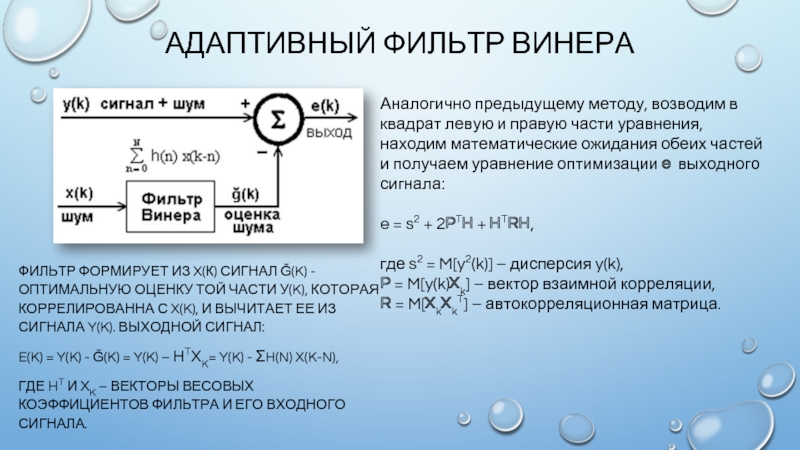
Слайд 5АДАПТИВНЫЙ ФИЛЬТР ВИНЕРА
ФИЛЬТР ФОРМИРУЕТ ИЗ X(К) СИГНАЛ Ğ(K) - ОПТИМАЛЬНУЮ ОЦЕНКУ
E(K) = Y(K) - Ğ(K) = Y(K) – HTXK= Y(K) - ΣH(N) X(K-N),
ГДЕ HT И XK – ВЕКТОРЫ ВЕСОВЫХ КОЭФФИЦИЕНТОВ ФИЛЬТРА И ЕГО ВХОДНОГО СИГНАЛА.
Аналогично предыдущему методу, возводим в квадрат левую и правую части уравнения, находим математические ожидания обеих частей и получаем уравнение оптимизации e выходного сигнала:
e = s2 + 2PTH + HTRH,
где s2 = M[y2(k)] – дисперсия y(k),
P = M[y(k)Xk] – вектор взаимной корреляции,
R = M[XkXkT] – автокорреляционная матрица.
Слайд 6В СТАЦИОНАРНОЙ СРЕДЕ ГРАФИК ЗАВИСИМОСТИ E ОТ КОЭФФИЦИЕНТОВ H ПРЕДСТАВЛЯЕТ СОБОЙ
D = DE / DH = -2P + 2RH.
В ТОЧКЕ МИНИМУМА ГРАДИЕНТ РАВЕН НУЛЮ И ВЕКТОР ВЕСОВЫХ КОЭФФИЦИЕНТОВ ФИЛЬТРА ЯВЛЯЕТСЯ ОПТИМАЛЬНЫМ:
HOPT = R-1P (УРАВНЕНИЕ ВИНЕРА – ХОЛФА)
ЗАДАЧЕЙ АЛГОРИТМА АВТОМАТИЧЕСКОЙ НАСТРОЙКИ ЯВЛЯЕТСЯ ПОДБОР ТАКИХ ВЕСОВЫХ КОЭФФИЦИЕНТОВ ФИЛЬТРА, КОТОРЫЕ ОБЕСПЕЧИВАЮТ РАБОТУ В ОПТИМАЛЬНОЙ ТОЧКЕ ПОВЕРХНОСТИ АДАПТАЦИИ.
Слайд 7АДАПТИВНЫЙ АЛГОРИТМ НАИМЕНЬШИХ КВАДРАТОВ УИДРОУ-ХОПФА
ПО СУЩЕСТВУ, ЭТО МОДИФИКАЦИЯ ФИЛЬТРА ВИНЕРА, В
HK+1 = HK - MEK XK
EK = YK - HT XK
УСЛОВИЕ СХОДИМОСТИ К ОПТИМУМУ:
0 < M > 1/LMAX
ГДЕ M - ПАРАМЕТР СКОРОСТИ СПУСКА, LMAX – МАКСИМАЛЬНОЕ СОБСТВЕННОЕ ЗНАЧЕНИЕ КОВАРИАЦИОННОЙ МАТРИЦЫ ДАННЫХ.
НА ПРАКТИКЕ ТОЧКА МАКСИМАЛЬНОЙ ОПТИМАЛЬНОСТИ ФЛЮКТУИРУЕТ ОКОЛО ТЕОРЕТИЧЕСКИ ВОЗМОЖНОЙ. ЕСЛИ ВХОДНОЙ СИГНАЛ НЕСТАЦИОНАРНЫЙ, ТО ИЗМЕНЕНИЕ СТАТИСТИК СИГНАЛА ДОЛЖНО ПРОИСХОДИТЬ ДОСТАТОЧНО МЕДЛЕННО, ЧТОБЫ КОЭФФИЦИЕНТЫ ФИЛЬТРА УСПЕВАЛИ СЛЕДИТЬ ЗА ЭТИМИ ИЗМЕНЕНИЯМИ.
Слайд 8РЕКУРСИВНЫЕ СХЕМЫ НАИМЕНЬШИХ КВАДРАТОВ
ОТЛИЧАЕТСЯ ТЕМ, ЧТО ВЫЧИСЛЕНИЕ КАЖДОЙ ПОСЛЕДУЮЩЕЙ ВЫБОРКИ КОЭФФИЦИЕНТОВ
ИМЕЕТ ЗНАЧИТЕЛЬНО БОЛЕЕ ВЫСОКУЮ ВЫЧИСЛИТЕЛЬНУЮ СЛОЖНОСТЬ, НО ОДНОВРЕМЕННО БОЛЬШУЮ СКОРОСТЬ СХОДИМОСТИ (БЫСТРОДЕЙСТВИЕ) И ТОЧНОСТЬ.
Слайд 9СРАВНЕНИЕ РЕЗУЛЬТАТОВ ФИЛЬТРАЦИИ С ЗАДАННЫМИ ПАРАМЕТРАМИ (В ЦЕНТРЕ) И РЕЗУЛЬТАТОВ АДАПТИВНОЙ
Слайд 11ИТОГИ:
НАИБОЛЕЕ ВАЖНОЙ ЧАСТЬЮ АДАПТИВНОГО КОМПЕНСАТОРА ПОМЕХ ЯВЛЯЕТСЯ УСТРОЙСТВО УПРАВЛЕНИЯ ВЕСОВЫМИ КОЭФФИЦИЕНТАМИ
ЗАДАЧА АДАПТИВНОЙ КОМПЕНСАЦИИ ПОМЕХИ СВОДИТСЯ К ПОДБОРУ КОЭФФИЦИЕНТОВ ФИЛЬТРА ТАКИМ ОБРАЗОМ, ЧТОБЫ МИНИМИЗИРОВАТЬ ЭНЕРГИЮ СИГНАЛА НА ВЫХОДЕ КОМПЕНСАТОРА . В ЭТОМ СЛУЧАЕ БУДЕТ МАКСИМИЗИРОВАНО ВЫХОДНОЕ ОТНОШЕНИЕ СИГНАЛ/ШУМ. МИНИМИЗАЦИЯ ЭНЕРГИИ ОБЫЧНО ОСУЩЕСТВЛЯЕТСЯ НА ОСНОВЕ ГРАДИЕНТНЫХ МЕТОДОВ ПОИСКА ЭКСТРЕМУМА ФУНКЦИЙ МНОГИХ ПЕРЕМЕННЫХ.
ИЗВЕСТНО, ЧТО АДАПТИВНЫЕ КОМПЕНСАТОРЫ ПОМЕХ ПОЗВОЛЯЮТ ЗНАЧИТЕЛЬНО УЛУЧШИТЬ КАЧЕСТВО ЗАШУМЛЕННЫХ СИГНАЛОВ, НО ТРЕБОВАНИЕ НАЛИЧИЯ ОПОРНОГО СИГНАЛА СУЩЕСТВЕННО СУЖАЕТ ИХ ОБЛАСТЬ ПРИМЕНЕНИЯ.
Слайд 12СПИСОК ЛИТЕРАТУРЫ
А.В. ДАВЫДОВ «ЦИФРОВАЯ ОБРАБОТКА СИГНАЛОВ», 2005
В.И.ДЖИГАН «АДАПТИВНЫЕ ФИЛЬТРЫ. СОВРЕМЕННЫЕ СРЕДСТВА
В.И.ДЖИГАН «АДАПТИВНАЯ ФИЛЬТРАЦИЯ: ТЕОРИЯ И АЛГОРИТМЫ», 2013
МАТЕРИАЛ ИЗ НАЦИОНАЛЬНОЙ БИБЛИОТЕКИ ИМ. Н. Э. БАУМАНА «АДАПТИВНАЯ ФИЛЬТРАЦИЯ ЦИФРОВЫХ ДАННЫХ», 2016
Слайд 13ВОПРОСЫ К ЗАЧЁТУ
ТРИ ОСНОВНЫЕ ПРИЧИНЫ ПРИМЕНЕНИЯ АДАПТИВНЫХ ФИЛЬТРОВ
НАИБОЛЕЕ РАСПРОСТРАНЕННЫЕ СХЕМЫ АДАПТИВНОЙ
СХЕМА УСТРОЙСТВА АДАПТИВНОГО ШУМОПОДАВИТЕЛЯ