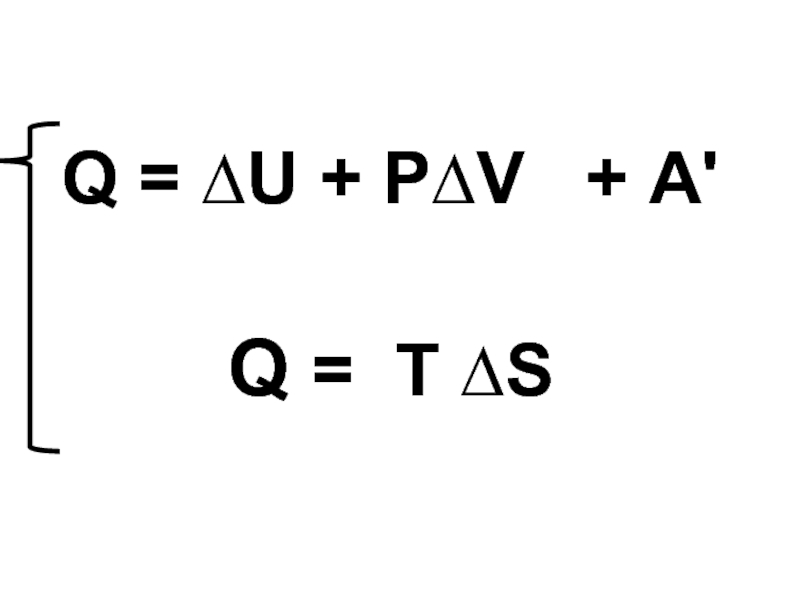- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Второй закон термодинамики. Биоэнергетика презентация
Содержание
- 1. Второй закон термодинамики. Биоэнергетика
- 2. План 2.1 Второй закон термодинамики. Энтропия 2.2 Свободная энергия Гиббса. 2.3 Биоэнергетика
- 3. 2.1 Химические реакции и физико-химические процессы можно
- 4. Самопроизвольные процессы протекают без сообщения системе дополнительной энергии из окружающей среды.
- 5. Самопроизвольно протекают процессы Растворения Диффузии Осмоса Расширения газа в пустоту
- 6. Пределом протекания самопроизвольных процессов является состояние термодинамического равновесия.
- 7. Термодинамическое равновесие – это такое состояние системы,
- 8. Система, находящаяся в равновесии, не способна выполнять работу.
- 9. Термодинамическое равновесие достигается только в закрытых и
- 10. Для открытых систем аналогом равновесного является стационарное
- 11. Стационарное состояние характеризуется длительным постоянством термодинамических параметров системы и одновременной способностью совершать полезную работу.
- 12. Для протекания несамопроизвольных процессов необходимо сообщить системе
- 13. Одним из фундаментальных свойств природы является ее ассиметрия. Ассиметрия природных процессов проявляется в их однонаправленности.
- 14. самопроизвольный (гликолиз)
- 15. Рассмотрение вопросов о характере протекания процессов выполняется в рамках второго закона термодинамики.
- 16. Второй закон термодинамики был сформулирован на основе анализа действия тепловых машин.
- 17. Тепловая машина – это устройство, в котором тепловая энергия превращается в механическую работу.
- 18. Нагреватель Холодильник
- 19. Теоремы Карно: 1) Коэффициент полезного действия
- 20. 2) Коэффициент полезного действия тепловой машины всегда меньше единицы.
- 21. А
- 22. К.п.д. даже самых современных тепловых машин невысок:
- 23. К.п.д. превращения химической энергии пищи – 25
- 24. Формулировки второго закона: 1) Невозможно
- 25. 2) Невозможен процесс, единственный результат которого состоял
- 26. Для математического описания Второго закона термодинамики используется термодинамическая функция состояния, называемая Энтропией (S, Дж/К)
- 27. Термин «Энтропия» был предложен Клаузиусом в 1865.
- 28. Энтропия(S) –
- 29. Энтропия является единственной функцией состояния, имеющей два толкования: Термодинамическое, Статистическое
- 30. Термодинамическое толкование энтропии Энтропия является характеристикой тепловых потерь системы в данном интервале температур.
- 31. Энтропия характеризует ту часть теплоты, которая рассеивается в пространстве, не превращаясь в полезную работу.
- 32. Чем больше энтропия, тем ниже «качество энергии» (меньше к.п.д. процесса)
- 33. Взаимосвязь энтропии, теплоты и температуры описывается неравенством
- 34. Клаузиус предложил обобщенную формулировку первого и второго законов: «Энергия мира постоянна, его энтропия постоянно увеличивается»
- 35. Статистическое толкование энтропии Статистическое толкование энтропии было предложено Л.Больцманом в 1904 г.
- 36. Статистическая термодинамика рассматривает энергетическое состояние системы, исходя из состояния ее структурных единиц.
- 37. Уравнение Больцмана где k - константа Больцмана
- 38. W - термодинамическая вероятность системы, т.е. число микросостояний, посредством которых реализуется данное макросостояние.
- 39. Микросостояние – это скорость, энергия, импульс движения
- 40. ← ↑ → ↑ ↑
- 41. Энтропия– количественная мера беспорядка в системе. Чем больше энтропия системы, тем больше беспорядок в ней.
- 42. Порядок Беспорядок ● ●
- 43. Самопроизвольные процессы протекают с ростом энтропии. Максимум энтропии достигается в состоянии равновесия (формулировка Л.Больцмана)
- 44. Изменение энтропии открытых стационарных систем было
- 45. Теорема И. Пригожина (1946): в стационарной термодинамически
- 46. Теорема И. Пригожина объясняет причину гомеостаза- постоянства
- 47. Расчет энтропии химической реакции (ΔrS) по следствию
- 48. Если ΔrS > 0 => реакция протекает
- 49. 2.2 При протекании химических процессов наблюдаются две противоположные тенденции.
- 50. стремление отдельных частиц соединится в более крупные
- 51. стремление агрегатов к разделению на более мелкие
- 52. G = H - TS Обе тенденции
- 53. Дж.У.Гиббс (11.II.1839 - 28.IV.1903) Американский физик
- 54. Физический смысл Свободной энергии Гиббса понятен из совместного рассмотрения первого и второго законов термодинамики.
- 55. Q = ∆U + P∆V
- 56. Отсюда A' = TΔS - ΔU
- 57. Следовательно, A'
- 58. A' = - ΔG
- 59. G – это часть внутренней энергии системы, способная превращаться в полезную работу.
- 60. Знак ΔG (+ или –) является критерием возможности протекания самопроизвольных процессов в закрытых системах.
- 61. Самопроизвольный процесс: A′ > 0
- 62. Таким образом,
- 63. Характер процесса иногда можно изменять, варьируя термодинамические
- 64. Влияние температуры на характер процесса ΔG
- 65. ΔG = ΔН
- 66. ΔG = ΔН
- 67. ΔG = ΔН –
- 68. Рассчитав ΔG, можно определить: характер
- 69. Способы расчета ΔG 1. Свободную энергию
- 70. 2. Свободную энергию химической реакции можно рассчитать
- 71. 3. Расчет ΔG переноса вещества из одной
- 72. Данное уравнение можно использовать для расчета осмотической работы, выполняемой почкой.
- 73. 2.3 Биоэнергетика – это раздел термодинамики, изучающий превращения энергии, теплоты и работы в живых системах.
- 74. Человек – это открытая стационарная система, главным
- 75. Энергетические затраты человека обеспечиваются за счет:
- 76. Получаемая энергия расходуется на: Совершение работы
- 77. Коэффициент полезного действия превращения химической энергии пищи
- 78. Таким образом, энтропийные потери организма составляют 75%.
- 79. Биохимическими называются химические реакции, протекающие в биосистемах
- 80. Окисление углеводов и жиров в организме протекает
- 81. Часть энергии, выделяющаяся при окислении компонентов пищи,
- 82. При физиологических условиях синтез АТФ протекает совместно
- 83. Такие реакции называются сопряженными. Принцип энергетического сопряжения
- 84. Как правило, сопряженные реакции катализируются общим ферментом.
- 85. Схема сопряженной реакции A + B →
- 86. Пример энергетического сопряжения : C6H12O6 +
- 87. Приведенные данные позволяют рассчитать к.п.д. клетки:
- 88. Таким образом, клетка аккумулирует лишь 38% химической
- 89. В современной медицине широко применяются методы биоэнергетической
- 90. Гирудотерапия (лечение медицинскими пиявками)
- 91. Массаж
- 92. Упражнения по системе Йоги и др.
- 93. Благодарим за внимание!!!
План 2.1 Второй закон термодинамики. Энтропия 2.2 Свободная энергия Гиббса. 2.3 Биоэнергетика
Слайд 32.1 Химические реакции и физико-химические процессы можно разделить на две группы:
самопроизвольные (спонтанные)
несамопроизвольные
(неспонтанные)
Слайд 4Самопроизвольные процессы протекают без сообщения системе дополнительной энергии из окружающей среды.
Слайд 6Пределом протекания самопроизвольных процессов является состояние термодинамического равновесия.
Слайд 7Термодинамическое равновесие – это такое состояние системы, в котором ее термодинамические
параметры (T, p, V и др.) не изменяются во времени и имеют одинаковое значение во всех точках объема системы.
Слайд 9Термодинамическое равновесие достигается только в закрытых и изолированных системах. Оно не
достижимо для открытых систем из-за постоянно изменяющихся внешних условий.
Слайд 10Для открытых систем аналогом равновесного является стационарное состояние, обусловленное сбалансированностью потоков
энергии и вещества в систему и из системы.
Слайд 11Стационарное состояние характеризуется длительным постоянством термодинамических параметров системы и одновременной способностью
совершать полезную работу.
Слайд 12Для протекания несамопроизвольных процессов необходимо сообщить системе дополнительную энергию. Например, фотосинтез,
протекающий под воздействием УФ излучения.
Слайд 13Одним из фундаментальных свойств природы является ее ассиметрия. Ассиметрия природных процессов
проявляется в их однонаправленности.
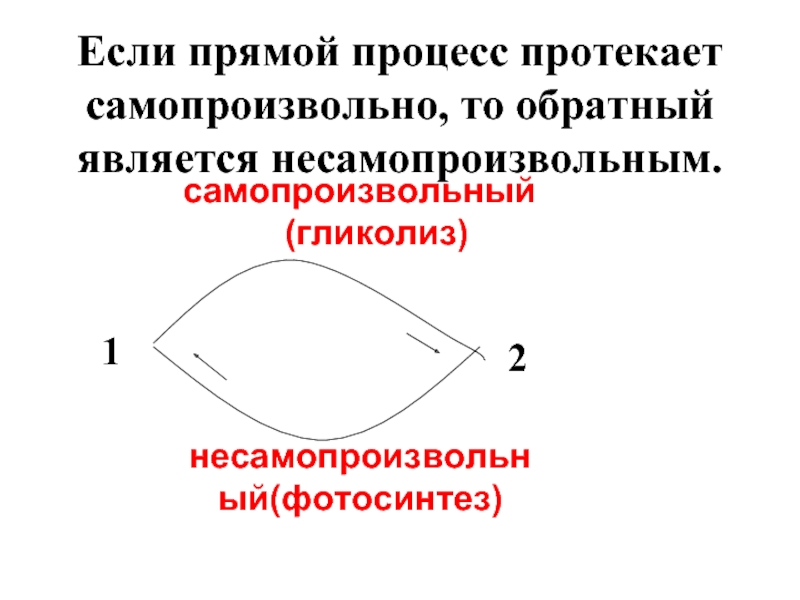
Слайд 14
самопроизвольный
(гликолиз)
несамопроизвольный(фотосинтез)
1
2
Если прямой процесс протекает самопроизвольно,
то обратный является несамопроизвольным.
Слайд 15Рассмотрение вопросов о характере протекания процессов выполняется в рамках второго закона
термодинамики.
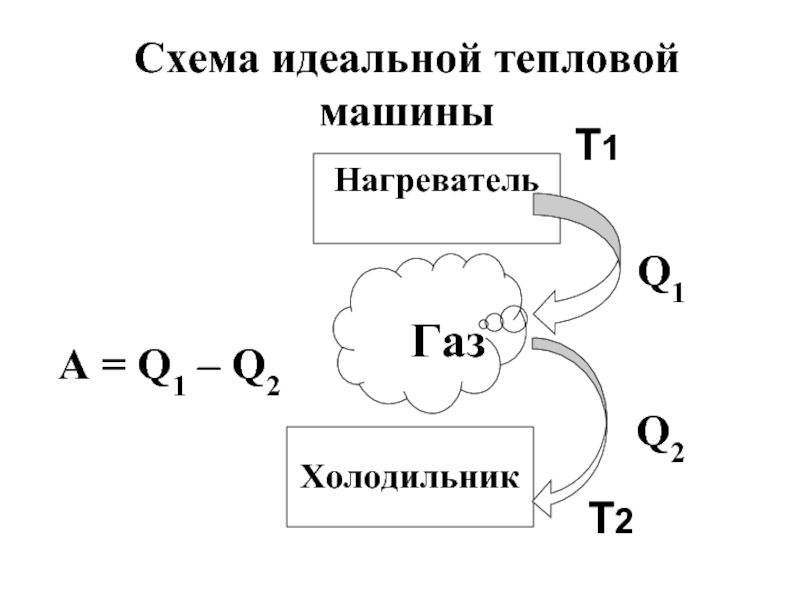
Слайд 17Тепловая машина – это устройство, в котором тепловая энергия превращается в
механическую работу.
Слайд 19Теоремы Карно:
1) Коэффициент полезного действия тепловой машины, не зависит от рода
рабочего тела, а только от температур нагревателя и холодильника.
Слайд 21 А Q1 – Q2
Т1 – Т2
к.п.д. = = ≤ ,
Q1 Q1 Т1
Уравнение Карно
Поскольку Т2 ≠ 0, (абсолютный нуль не достижим), то к.п.д. < 1
Слайд 22К.п.д. даже самых современных тепловых машин невысок:
для тепловозов – 20
%,
двигателей внутреннего сгорания – 30 %.
двигателей внутреннего сгорания – 30 %.
Слайд 23К.п.д. превращения химической энергии пищи – 25 %,
к.п.д. превращения
энергии АТФ в работу мышц ~ 50 % ,
К.п.д. здорового сердца – 43 %.
К.п.д. здорового сердца – 43 %.
Слайд 24Формулировки второго закона:
1) Невозможно полностью превратить теплоту в работу (У.
Кельвин 1851 ).
Слайд 252) Невозможен процесс, единственный результат которого состоял бы в переходе энергии
от холодного тела к горячему (Клаузиус, 1865).
Слайд 26 Для математического описания Второго закона термодинамики используется термодинамическая функция состояния,
называемая Энтропией (S, Дж/К)
Слайд 29Энтропия является единственной функцией состояния, имеющей два толкования:
Термодинамическое,
Статистическое
Слайд 30Термодинамическое толкование энтропии
Энтропия является характеристикой тепловых потерь системы в данном интервале
температур.
Слайд 31Энтропия характеризует ту часть теплоты, которая рассеивается в пространстве, не превращаясь
в полезную работу.
Слайд 34Клаузиус предложил обобщенную формулировку первого и второго законов: «Энергия мира постоянна,
его энтропия постоянно увеличивается»
Слайд 35
Статистическое толкование энтропии
Статистическое толкование энтропии было предложено Л.Больцманом в 1904 г.
Слайд 36
Статистическая термодинамика рассматривает энергетическое состояние системы, исходя из состояния ее структурных
единиц.
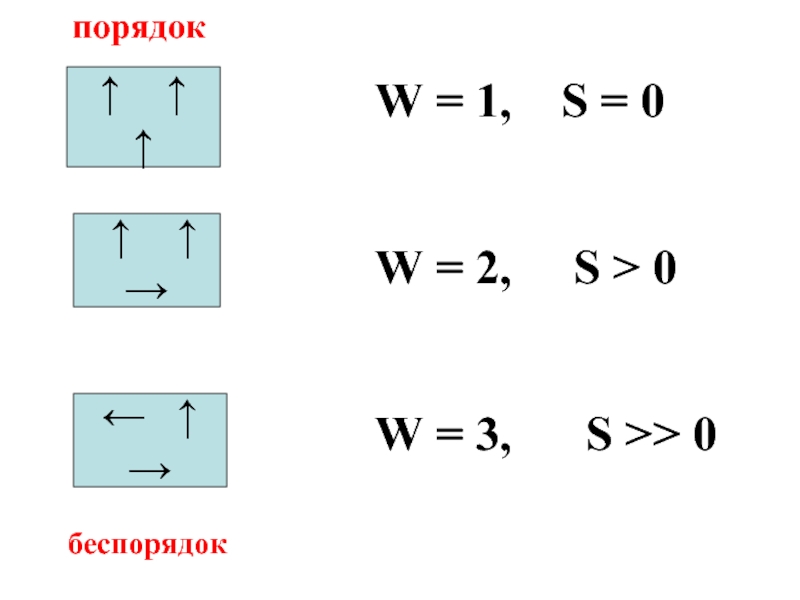
Слайд 38W - термодинамическая вероятность системы, т.е. число микросостояний, посредством которых реализуется
данное макросостояние.
Слайд 39Микросостояние – это скорость, энергия, импульс движения и другие характеристики каждой
отдельно взятой структурной единицы. Чем меньше число микросостояний, тем выше упорядоченность системы.
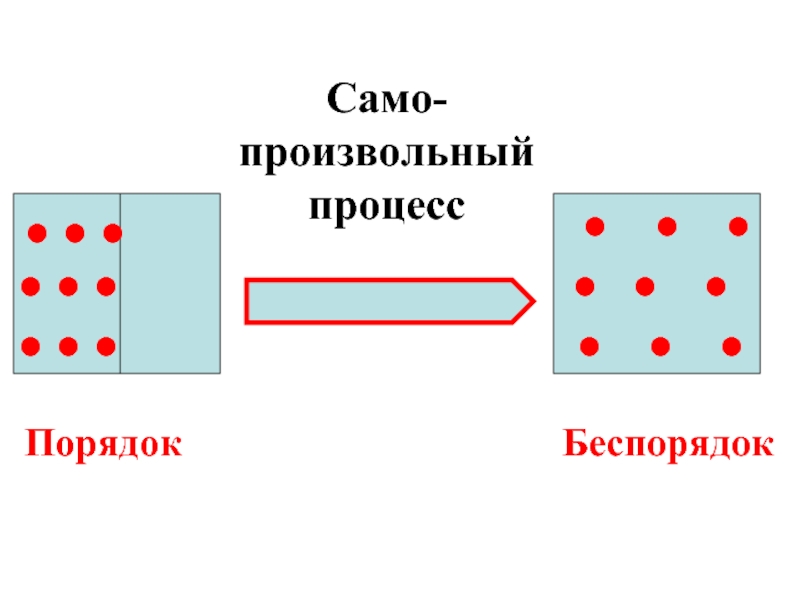
Слайд 41Энтропия– количественная мера беспорядка в системе.
Чем больше энтропия системы, тем больше
беспорядок в ней.
Слайд 43Самопроизвольные процессы протекают с ростом энтропии. Максимум энтропии достигается в состоянии
равновесия (формулировка Л.Больцмана)
Слайд 45Теорема И. Пригожина (1946): в стационарной термодинамически открытой системе скорость производства
энтропии, обусловленного протеканием в ней самопроизвольных процессов, принимает минимальное положительное значение:
ΔSi
→ 0
τ
Слайд 46Теорема И. Пригожина объясняет причину гомеостаза- постоянства внутренний среды организма. Она
не применима к описанию процессов, протекающих в организме новорожденных, так как они протекают со значительной скоростью
Слайд 47Расчет энтропии химической реакции (ΔrS) по следствию из закона Гесса
Для условной
реакции:
аА + bВ → сС + dD
аА + bВ → сС + dD
ΔrS = cS (C) + dS (D) – aS (A) – bS (B)
Слайд 48Если ΔrS > 0 => реакция протекает с увеличением беспорядка;
Если ΔrS
< 0 => реакция протекает с уменьшением беспорядка.
Слайд 50стремление отдельных частиц соединится в более крупные агрегаты, что приводит к
уменьшению запаса внутренней энергии системы: H → min;
Слайд 51стремление агрегатов к разделению на более мелкие частицы, что приводит к
увеличению энтропии: S → max
Слайд 52G = H - TS
Обе тенденции находят свое отражение в термодинамической
функции состояния, называемой свободной энергией Гиббса или изобарно-изотермическим потенциалом G:
ΔG = ΔH - TΔS
Слайд 53
Дж.У.Гиббс (11.II.1839 - 28.IV.1903)
Американский физик и химик, один из основоположников классической
термодинамики, профессор в Йельском университете. Он первым применил термодинамические законы для описания биологических систем.
Слайд 54Физический смысл Свободной энергии Гиббса понятен из совместного рассмотрения первого и
второго законов термодинамики.
Слайд 60Знак ΔG (+ или –) является критерием возможности протекания самопроизвольных процессов
в закрытых системах.
Слайд 61Самопроизвольный процесс:
A′ > 0 ∆G
0
Термодинамическое равновесие:
A′ = 0 ∆G = 0
Несамопроизвольный процесс:
A′ < 0 ∆G > 0
Термодинамическое равновесие:
A′ = 0 ∆G = 0
Несамопроизвольный процесс:
A′ < 0 ∆G > 0
Слайд 62Таким образом, самопроизвольно осуществляются те процессы,
протекание которых сопровождается уменьшением свободной энергии Гиббса.
Слайд 63Характер процесса иногда можно изменять, варьируя термодинамические параметры системы: температуру, давление
или концентрацию реагирующих веществ.
Слайд 64Влияние температуры на характер процесса
ΔG = ΔН –
ТΔS
(–) (+)
Экзотермический Увеличение
процесс беспорядка
В этом случае ΔG < 0,
следовательно, самопроизвольный процесс протекает при любой температуре;
(–) (+)
Экзотермический Увеличение
процесс беспорядка
В этом случае ΔG < 0,
следовательно, самопроизвольный процесс протекает при любой температуре;
А)
Слайд 65
ΔG = ΔН – ТΔS
(–) (–)
Экзотермический Уменьшение процесс беспорядка
0<ΔG < 0
ΔG<0 при низкой Т, следовательно самопроизвольный процесс протекает при низкой температуре;
Экзотермический Уменьшение процесс беспорядка
0<ΔG < 0
ΔG<0 при низкой Т, следовательно самопроизвольный процесс протекает при низкой температуре;
Б)
Слайд 66
ΔG = ΔН – ТΔS
(+)
(+)
Эндотермический Увеличение
процесс беспорядка
0<ΔG < 0
ΔG <0 при высокой Т, следовательно самопроизвольный процесс протекает при высокой температуре;
Эндотермический Увеличение
процесс беспорядка
0<ΔG < 0
ΔG <0 при высокой Т, следовательно самопроизвольный процесс протекает при высокой температуре;
В)
Слайд 67ΔG = ΔН – ТΔS
(+)
(–)
Эндотермический Уменьшение
процесс беспорядка
ΔG > 0 при всех температурах, следовательно процесс является несамопроизвольным; он термодинамически запрещен.
Эндотермический Уменьшение
процесс беспорядка
ΔG > 0 при всех температурах, следовательно процесс является несамопроизвольным; он термодинамически запрещен.
Г)
Слайд 68 Рассчитав ΔG, можно определить:
характер процесса (само - или несамопроизвольный);
величину
полезной работы, совершаемой при протекании самопроизвольного процесса.
Слайд 69Способы расчета ΔG
1.
Свободную энергию химической реакции можно рассчитать по уравнению:
ΔrG = ΔrH – ТΔrS,
где ТΔrS – энтропийный фактор химической реакции
Слайд 702. Свободную энергию химической реакции можно рассчитать на основе закона Гесса:
ΔrG
= с ΔfG (C) + d ΔfG (D)- - a ΔfG (A) - b ΔfG (B)
где ∆fG- свободная энергия образования сложного вещества из простых веществ, kДж/моль
где ∆fG- свободная энергия образования сложного вещества из простых веществ, kДж/моль
Слайд 713. Расчет ΔG переноса вещества из одной фазы в другую:
ΔG =
– ν RT ln
где ν – количество переносимого вещества, моль;
R – универсальная газовая постоянная,
8,31 Дж/моль∙К;
СМ1 и CМ2 – концентрации вещества в различных фазах, моль/л (СМ1 < CМ2)
где ν – количество переносимого вещества, моль;
R – универсальная газовая постоянная,
8,31 Дж/моль∙К;
СМ1 и CМ2 – концентрации вещества в различных фазах, моль/л (СМ1 < CМ2)
CМ 2
CМ 1
Слайд 732.3 Биоэнергетика – это раздел термодинамики, изучающий превращения энергии, теплоты и
работы в живых системах.
Слайд 74Человек – это открытая стационарная система, главным источником энергии для которой
служит химическая энергия пищи (99 %).
Слайд 75Энергетические затраты человека обеспечиваются за счет:
углеводов на 55-60%,
жиров на 20-25%,
белков на 15-20%.
белков на 15-20%.
Слайд 76
Получаемая энергия расходуется на:
Совершение работы внутренних органов, связанной с дыханием, кровообращением,
перемещением метаболитов, секрецией соков и т.д.,
Совершение внешней работы, связанной со всеми перемещениями человека и его трудовой деятельностью,
Нагревание вдыхаемого воздуха, потребляемой воды и пищи.
Совершение внешней работы, связанной со всеми перемещениями человека и его трудовой деятельностью,
Нагревание вдыхаемого воздуха, потребляемой воды и пищи.
Слайд 77Коэффициент полезного действия превращения химической энергии пищи в организме человека составляет
~ 25 %.
Слайд 78Таким образом, энтропийные потери организма составляют 75%. Если сфокусировать теплоту, излучаемую
телом человека за сутки, то можно вскипятить 20 л воды.
Слайд 79Биохимическими называются химические реакции, протекающие в биосистемах (in vivo).
БИОХИМИЧЕСКИЕ РЕАКЦИИ
Экзергонические (самопроизвольные)
ΔrG < 0
Эндергонические (несамопроизвольные) ΔrG > 0
Эндергонические (несамопроизвольные) ΔrG > 0
Слайд 80Окисление углеводов и жиров в организме протекает самопроизвольно и сопровождается выделением
большого количества энергии:
C6H12O6 + 6 O2 → 6 CO2 + 6 H2O, ΔG = - 2870 кДж
C15H31COOH + 23 O2 → 16 CO2 +
Пальмитиновая к-та
+ 16 H2O, ΔG = - 9790 кДж
C6H12O6 + 6 O2 → 6 CO2 + 6 H2O, ΔG = - 2870 кДж
C15H31COOH + 23 O2 → 16 CO2 +
Пальмитиновая к-та
+ 16 H2O, ΔG = - 9790 кДж
Слайд 81Часть энергии, выделяющаяся при окислении компонентов пищи, накапливается в макроэргических соединениях,
таких как АТФ, АДФ, ацетилкофермент A и др.
АДФ + H3PO4 → АТФ + H2O,
∆G = + 30,6 кДж
Слайд 82При физиологических условиях синтез АТФ протекает совместно с окислением глюкозы до
СО2 и воды. Энергия, выделяющаяся при окислении одной молекулы глюкозы, достаточна для синтеза 36 молекул АТФ из АДФ и фосфата.
Слайд 83Такие реакции называются сопряженными. Принцип энергетического сопряжения состоит в следующим: эндергонические
реакции протекают за счет энергии экзергонических реакций.
Слайд 85Схема сопряженной реакции
A + B → C + D, ∆G1
0
L + M → P + Q, ∆G2 > 0
∆Gобщ = ∆G1 + ∆G2 <0
L + M → P + Q, ∆G2 > 0
∆Gобщ = ∆G1 + ∆G2 <0
Обе реакции протекают как единый самопроизвольный процесс
Слайд 86Пример энергетического сопряжения :
C6H12O6 + 6 O2 → 6 CO2 +
6 H2O, ΔG = - 2870 кДж
36 (AДФ + H3PO4) → 36 (ATФ + H2O), ΔG =+1100 кДж
--------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
ΔG общ. = - 2870 + 1100 = - 1770 кДж
36 (AДФ + H3PO4) → 36 (ATФ + H2O), ΔG =+1100 кДж
--------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
ΔG общ. = - 2870 + 1100 = - 1770 кДж
Слайд 87Приведенные данные позволяют рассчитать к.п.д. клетки:
Выделилось
2870 кДж,
Аккумулировано 1100 кДж ,
Энтропийные потери 1770 кДж
к.п.д = 1100/2870 = 0.38 or 38%
Аккумулировано 1100 кДж ,
Энтропийные потери 1770 кДж
к.п.д = 1100/2870 = 0.38 or 38%
Слайд 88Таким образом, клетка аккумулирует лишь 38% химической энергии глюкозы, а оставшиеся
62% рассеивается в пространстве как теплота.
Слайд 89В современной медицине широко применяются методы биоэнергетической диагностики и терапии. К
биоэнергетическим методам лечения относятся:
Иглотерапия
Иглотерапия
