- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Симметрия кристаллов, текстур и элементы кристаллофизики презентация
Содержание
- 1. Симметрия кристаллов, текстур и элементы кристаллофизики
- 2. Принцип Кюри Пьер Кюри (1859-1906) –
- 3. Систематика кристаллографических точечных групп *В группе 432 все пьезоэлектрические коэффициенты нулевые
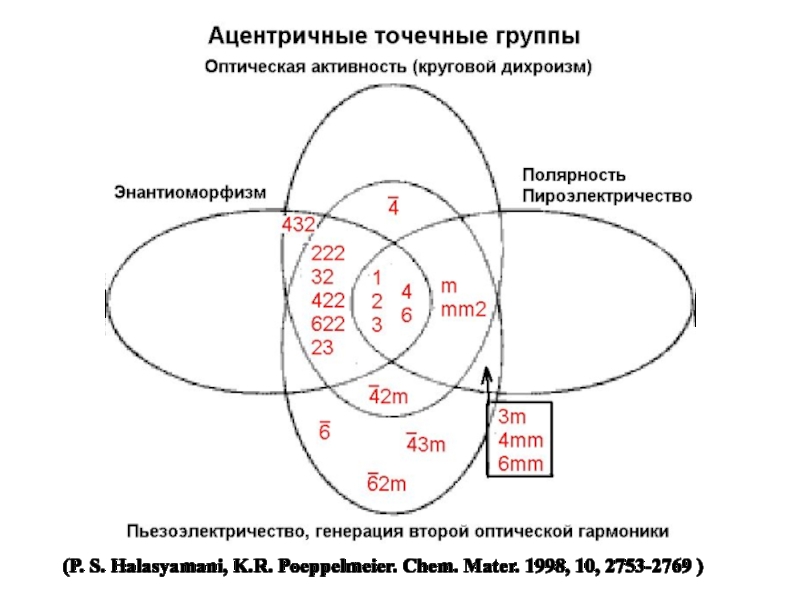
- 5. (P. S. Halasyamani, K.R. Poeppelmeier. Chem. Mater. 1998, 10, 2753-2769 )
- 6. Проблема обнаружения центра инверсии Согласно одному из
- 7. 3) Пироэлектрический эффект – возникновение поляризации при
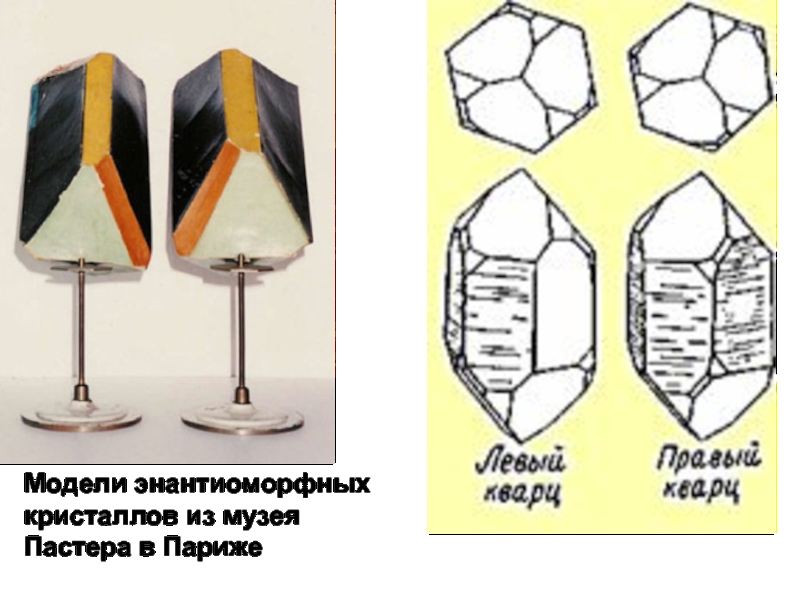
- 8. Модели энантиоморфных кристаллов из музея Пастера в Париже
- 9. 5) Вращение плоскости поляризации света (оптическая активность)
- 10. 7) В некоторых частных случаях наличие или
- 11. 8) На практике в большинстве случаев структурного
- 12. Тензорное и матричное описание физических свойств
- 13. Примеры тензоров разных рангов
- 14. Материальные тензоры второго ранга, описывающие соотношение между
- 15. Матрицы симметричных материальных тензоров второго ранга
- 16. Важный частный случай – одноосная пьезоэлектрическая
Слайд 1Симметрия кристаллов, текстур и элементы кристаллофизики
Текстура – поликристаллический материал, где ориентация
Некоторые предельные точечные группы – описывают симметрию полей и текстур с осями бесконечного порядка
Кристаллогр. Предельная Пример
группы группа
1, 2, 3, 4, 6 ∞ – вращающийся конус однородное магн. поле
2/m, -6, 4/m, 6/m ∞/m – вращающийся цилиндр ???
m, mm2, 3m, ∞ m – конус поле тяготения,
4mm, 6mm однородное электр. поле, пьезокерамический диск
mmm, -6m2, ∞/mmm – цилиндр одноосное давление
4/mmm, 6/mmm
[Желудев И.С. Физика кристаллических диэлектриков. 1968, с. 12]
Возможна и более низкая симметрия текстур, например, у листового проката - mmm
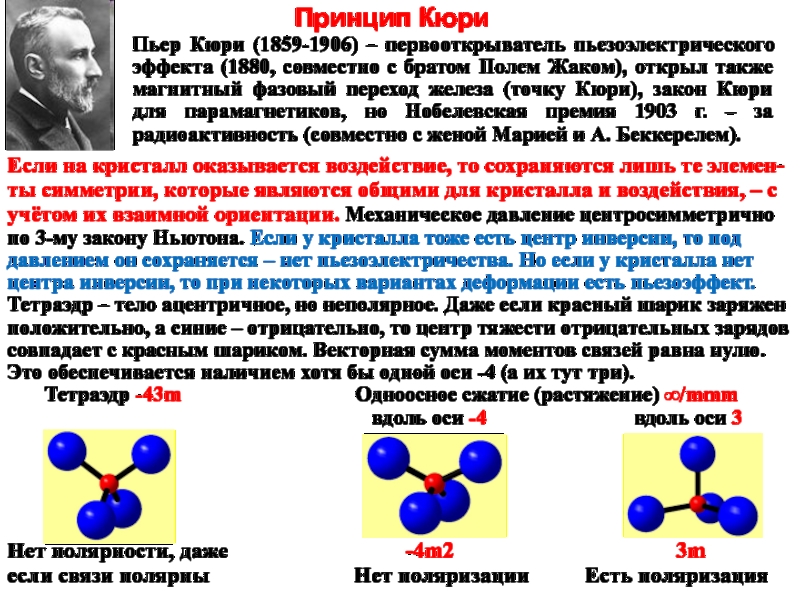
Слайд 2Принцип Кюри
Пьер Кюри (1859-1906) – первооткрыватель пьезоэлектрического эффекта (1880, совместно с
Если на кристалл оказывается воздействие, то сохраняются лишь те элемен-ты симметрии, которые являются общими для кристалла и воздействия, – с учётом их взаимной ориентации. Механическое давление центросимметрично по 3-му закону Ньютона. Если у кристалла тоже есть центр инверсии, то под давлением он сохраняется – нет пьезоэлектричества. Но если у кристалла нет центра инверсии, то при некоторых вариантах деформации есть пьезоэффект.
Тетраэдр – тело ацентричное, но неполярное. Даже если красный шарик заряжен положительно, а синие – отрицательно, то центр тяжести отрицательных зарядов совпадает с красным шариком. Векторная сумма моментов связей равна нулю. Это обеспечивается наличием хотя бы одной оси -4 (а их тут три).
Тетраэдр -43m Одноосное сжатие (растяжение) ∞/mmm
вдоль оси -4 вдоль оси 3
Нет полярности, даже -4m2 3m
если связи полярны Нет поляризации Есть поляризация
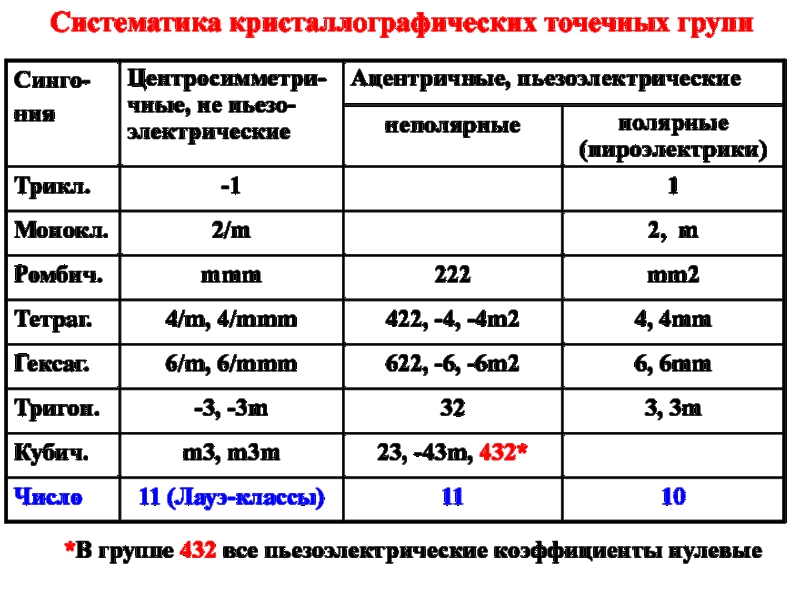
Слайд 3Систематика кристаллографических точечных групп
*В группе 432 все пьезоэлектрические коэффициенты нулевые
Слайд 6Проблема обнаружения центра инверсии
Согласно одному из законов оптики, закону Фриделя, дифракцион-ная
Известны следующие решения этой проблемы.
1) Отсутствие центра инверсии однозначно доказывается наличием пьезоэлектрического эффекта. Но с микрокристаллом, керамикой, проводящим кристаллом проверка этого обычно невозможна.
2) Отсутствие центра инверсии однозначно доказывается генераци-ей второй оптической гармоники (ГВГ), например, превращением ИК излучения лазера 1,06 мкм в зелёное 0,53 мкм. Это можно делать и с порошками, если кристаллы достаточно прозрачны, хотя для практических применений эффекта ГВГ нужны монокристаллы.
Слайд 73) Пироэлектрический эффект – возникновение поляризации при изменении температуры. Здесь те
4) Иногда отсутствие центра инверсии ярко выражено в форме кристаллов.
Кроме того, ацентричная форма могла получиться из-за условий роста по принципу Кюри. Если, например, кристалл растёт на дне стакана, то доступ вещества снизу затруднён, и там получается вмятина
– пирамида роста. Даже если структура имеет центр
инверсии или горизонтальную плоскость симметрии
или ось 2, то форма кристалла её теряет. А если внеш-
няя форма кристалла центросимметрична (например,
параллелепипед), это ещё не значит, что центр инверсии
действительно есть. Сегнетоэлектрики обычно растут
выше точки Кюри, а СЭ фазовый переход на форму не влияет.
Так Луи Пастер (1822-1895) в 1848 г. разделил пинцетом энантиомеры тартрата натрия-аммония. Но хорошо огранённые кристаллы получаются не всегда.
Слайд 95) Вращение плоскости поляризации света (оптическая активность) однозначно доказывает отсутствие центра
6) Аномальное рассеяние рентгеновских лучей. Закон Фриделя основан на том, что рентгеновские лучи рассеиваются атомами без изменения фазы. Но вблизи края поглощения происходит аномальное рассеяние с изменением фазы, и закон Фриделя нарушается: интенсивности отражений hkl и –h –k –l становятся неравными, если в кристалле нет центра инверсии. Их различие невелико, но современная аппаратура позволяет его обнаружить. Хуже другое: далеко не для каждого вещества (особенно если там нет тяжёлых атомов) можно подобрать трубку с излучением, близким к краю поглощения. В этом смысле очень ценно синхротронное излучение, из которого можно выбрать любую желаемую длину волны.
Даже если отсутствие центра инверсии уже установлено другими методами, аномальное рассеяние сохраняет решающее значение для определения абсолютных конфигураций оптически активных веществ, то есть позволяет рентгеновским методом различать "правые" и "левые" конфигурации атомных структур, что особенно важно для биохимии и молекулярной биологии. На некоторых монокристальных дифрактометрах есть сразу две рентгеновские трубки: жесткое излучение (MoKα) – для обычного структур-ного анализа, а более мягкое (CuKα, FeKα) – для аномального рассеяния.
Проблема обнаружения центра инверсии
Слайд 107) В некоторых частных случаях наличие или отсутствие центра инверсии доказывается
Проблема обнаружения центра инверсии
Слайд 118) На практике в большинстве случаев структурного анализа пытают-ся решить эту
Проблема обнаружения центра инверсии
Слайд 12Тензорное и матричное описание физических свойств
кристаллов и текстур
Скалярные величины достаточны
полевые тензоры – описывающие физические поля, воздействую-щие на кристалл или возникающие в кристалле в результате воздействия;
материальные тензоры, описывающие свойство материала, т.е. связь между воздействием и результатом.
Ранг материального тензора равен сумме рангов воздействия и результата. Пример. Если к кристаллу приложено электрическое поле, то в нём возникает ток. Это явление описывается удельной электропроводностью σ (См/м = А/(В м) по закону Ома:
j = σ E, где j – плотность тока (А/м2), E – напряжённость поля (В/м).
Но в анизотропной среде векторы j и E (тензоры 1 ранга) не обязательно параллельны! Направление тока не всегда точно совпадает с направлением поля! Поэтому σij – тензор 2-го ранга:
ji = σij Ej
Слайд 14Материальные тензоры второго ранга, описывающие соотношение между векторами
(теплопроводность, электропроводность, электросопротивление, диэлектрическая
Пусть вектор воздействия а определяется координатами а1, а2, а3, а вектор – результат с – координатами с1, с2, с3. Связь между ними задаётся системой уравнений: c1 = U11 a1 + U12 a2 + U13 a3
c2 = U21 a1 + U22 a2 + U23 a3
c3 = U31 a1 + U32 a2 + U33 a3
матрица коэффициентов которой описывает материальный тензор Uik:
В сокращённой записи ci = Uik ak
У такого тензора в общем случае 9 компонент, но перечисленные выше тензоры симметричны, т.е. Uik = Uki, и тогда число независимых компонент понижается до 6 в случае триклинной сингонии, и до меньшего числа при более высокой симметрии (см. следующий слайд).
Сокращённые обозначения индексов:
11→1, 22→2, 33→3, 23=32→4, 31=13→5, 12=21→6
Uik = | U1 U2 U3 U4 U5 U6 |
Измерив независимые компоненты, можно вычислить свойства
для любой ориентации
Слайд 15Матрицы симметричных материальных тензоров
второго ранга для разных сингоний
Триклинная:
Моноклинная: U1 U2 U3 0 U5 0 (если особая ось Y)
Ромбическая: U1 U2 U3 0 0 0
Средние: U1 U1 U3 0 0 0
Кубическая: U1 U1 U1 0 0 0
Заметьте, что число независимых компонент тензора второго ранга равно числу независимых параметров элементарной ячейки.
Матрицы симметричных материальных тензоров
третьего ранга для некоторых точечных классов
У центросимметричных кристаллов все компоненты тензора нечётного
ранга – нулевые, т.е. таких свойств (например, пиро- и пьезоэффекта) нет!
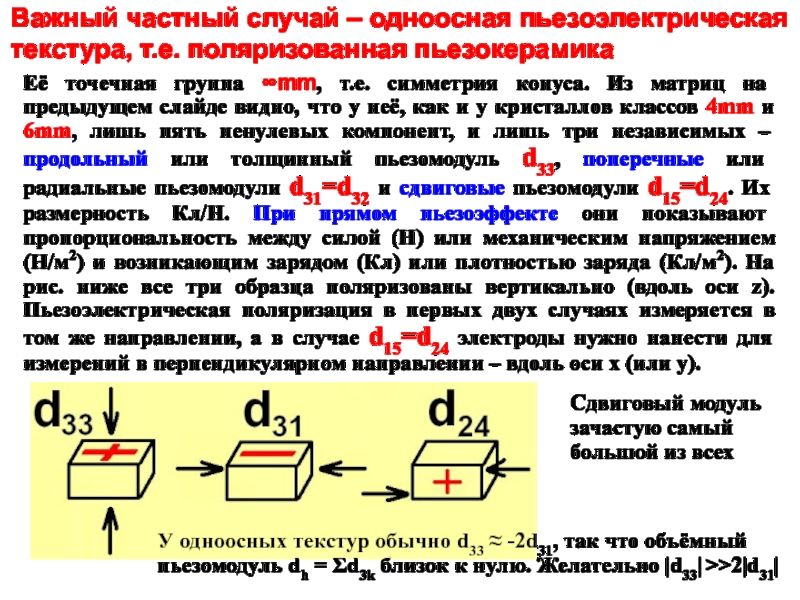
Слайд 16Важный частный случай – одноосная пьезоэлектрическая
текстура, т.е. поляризованная пьезокерамика
Её точечная
У одноосных текстур обычно d33 ≈ -2d31, так что объёмный пьезомодуль dh = Σd3k близок к нулю. Желательно |d33| >>2|d31|
Сдвиговый модуль
зачастую самый
большой из всех