Мембранный транспорт ионов: электродиффузионная теория презентация

движущей силе dμ/dx; u – подвижность иона

x – координата (расстояние).

Примеры линейных соотношений сил и потоков
(эл ток – закон Ома, диффузия – закон Фика, перенос тепла, поток воды).

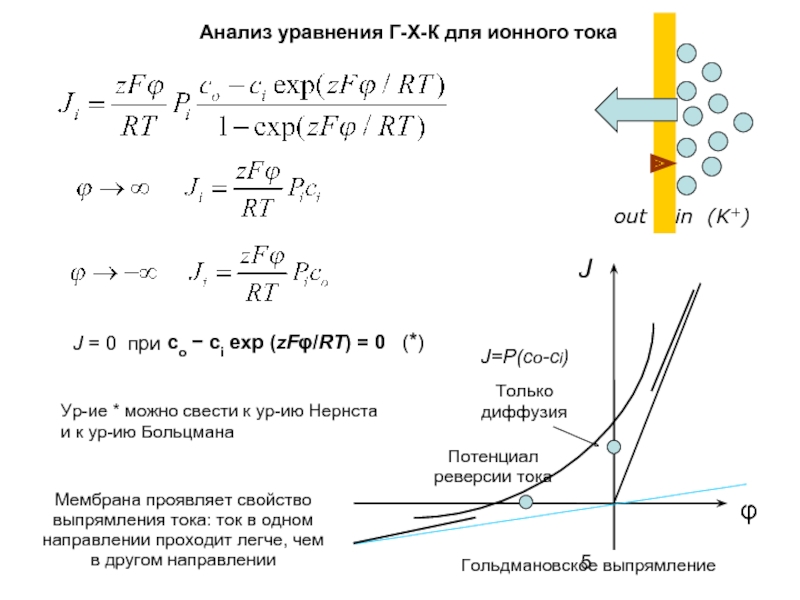
Уравнение Нерста-Планка Диффузия + миграция в эл. поле
Ур-ие описывает поток каждого вида ионов в отдельности.

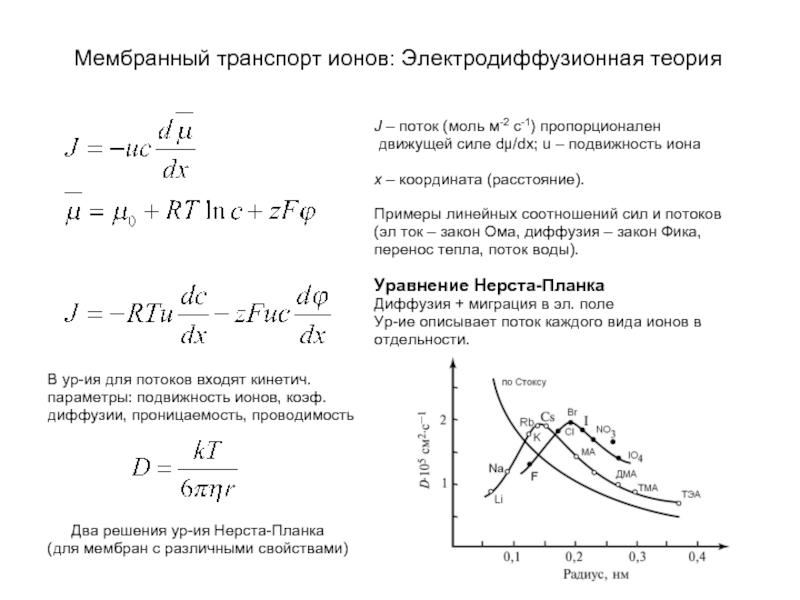
В ур-ия для потоков входят кинетич. параметры: подвижность ионов, коэф. диффузии, проницаемость, проводимость

Два решения ур-ия Нерста-Планка (для мембран с различными свойствами)

стеклянных микропипеток, в электродах сравнения и пр.

Конц-ии c+ и c− совпадают при любом x: J+ = J−, c+ = c−= c
В этом случае соблюдается условие электронейтральности по всей мембране, т.е.

Упражнение: На основе ур-ия Нернста-Планка





вывести формулу (Планка-Гендерсона) для диф. потенциала:

Упражнение: Определить величину и полярность Δφ на торце пипетки при её заполнении 1 М раствором NaCl и погружении в 1 мМ раствор NaCl.
Подвижность uNa = 5.2·10-8 м2 с-1·В-1, uCl = 7.9 10-8 м2 с-1·В-1. Для грубой оценки можно принять uCl ≈ 1.5 uNa

С- (см. «равновесие на границе масло-вода»)

(2) Теория постоянного эл. поля

Исходные постулаты:
- Мембрана - однородная сплошная среда, где происходят диффузия и миграция ионов;
- При отсутствии трансмембранной разности эл потенциалов (РЭП) эл. поля в мембране нет, а при наличии РЭП эл поле в мембране меняется линейно.
- Ионы движутся в мембране независимо друг от друга, не взаимодействуя между собой
- Конц-ии ионов на двух сторонах внутри мембраны пропорциональны конц-ям в каждом из контактирующих растворов с коэф-том пропорциональности γ ( γ –коэф. распределения).

φ=φm мембранный потенциал
h толщина мембраны

Т.к. эл потенциал меняется в мембране линейно, то

Ур-ие Нернста-Планка сводится к линейному диф. уравнению с одной переменной – с (а не с двумя переменными - c и φ).

Исходно

интегрировании dc/dx от x=0 до x=h получим конц-ии на краях внутри мембраны. Можно перейти к конц-иям в водных р-рах с учетом коэф-та γ. Получим (без вывода):

где

P – проницаемость
γ – коэф. распределения «мембрана – вода»

Ур-ие Гольдмана-Ходжкина- Каца для ионного тока

С учетом размерности входящих величин – u [м2 с-1 В-1] P = uRTγ/(zFh) uRT/(zF)=D P=Dγ/h

проходит легче, чем в другом направлении

J = 0 при

co − ci exp (zFφ/RT) = 0 (*)

Ур-ие * можно свести к ур-ию Нернста и к ур-ию Больцмана

Гольдмановское выпрямление

Только диффузия

Анализ уравнения Г-Х-К для ионного тока

J=P(co-ci)

(прямая зависимость тока от потенциала)

Поток в-ва в молях.



Эл. ток (перенос зарядов)



Проводимость. Размерность: Ом−1 = Сименс (См)

Упражнение: Найти диапазон изменений проводимости при варьировании РЭП на мембране.

Упражнение: рассчитать проводимость K-селективной мембраны (PK=4 10-10 м/с), омываемой 0.1 М раствором KCl.

эквивалентной цепи, содержащей два параллельных участка с эдс Е1, Е2 и проводимостями g1, g2 (1/R1,1/ R2).

эквивалентной цепи, содержащей два параллельных участка с эдс Е1, Е2 и проводимостями g1, g2 (1/R1,1/ R2).

A

эквивалентной цепи, содержащей два параллельных участка с эдс Е1, Е2 и проводимостями g1, g2 (1/R1,1/ R2).

градиентами эл потенциала и концентрации (при отсутствии взаимодействия). φ0 – равновесный потенциал, φ– мембранный потенциал.