- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
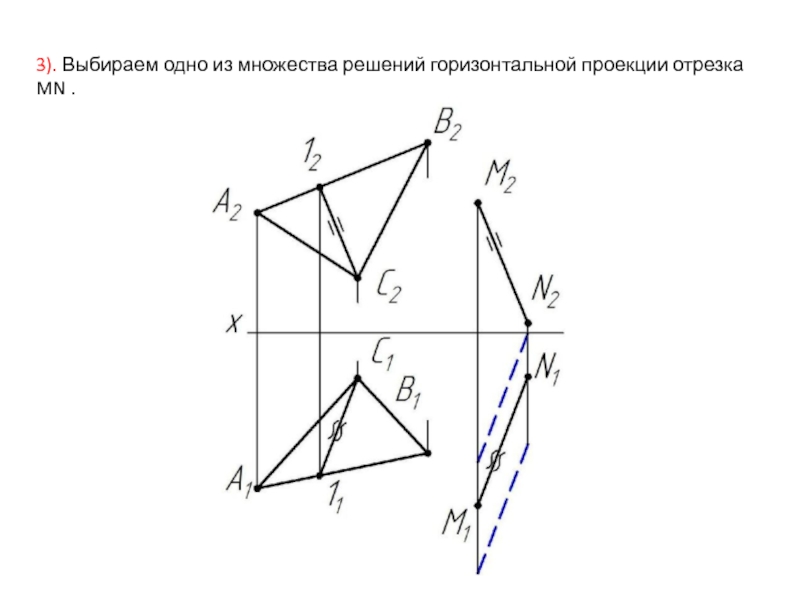
- Информатика
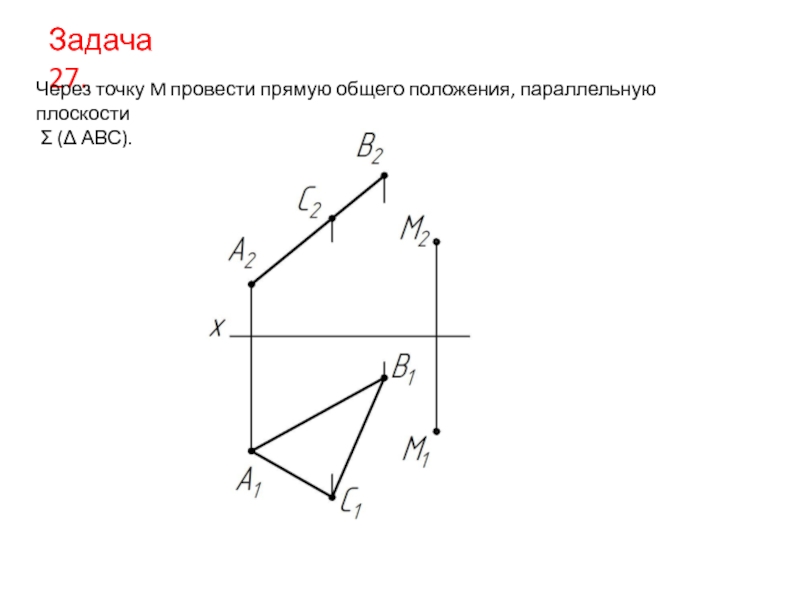
- История
- Литература
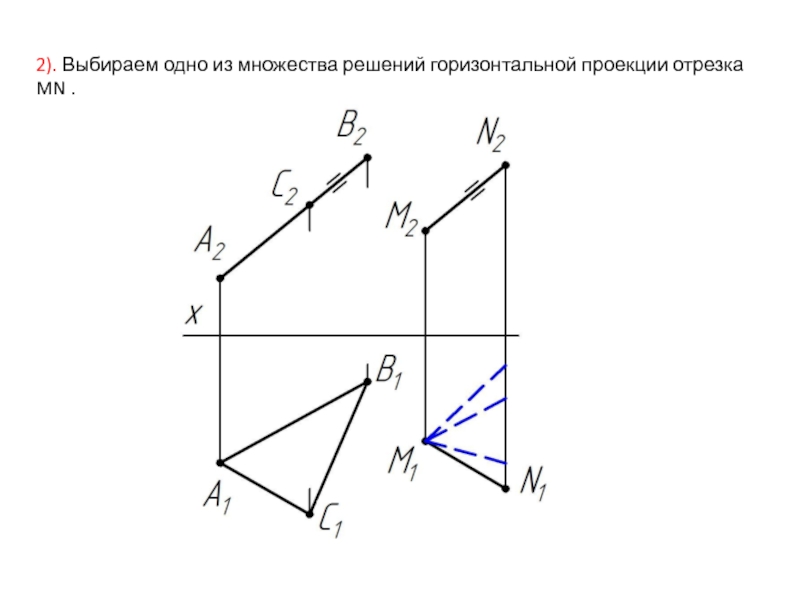
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Задачи 22-33 по инженерной графике презентация
Содержание
- 1. Задачи 22-33 по инженерной графике
- 2. Задача 22. Достроить горизонтальные проекции плоского многоугольника
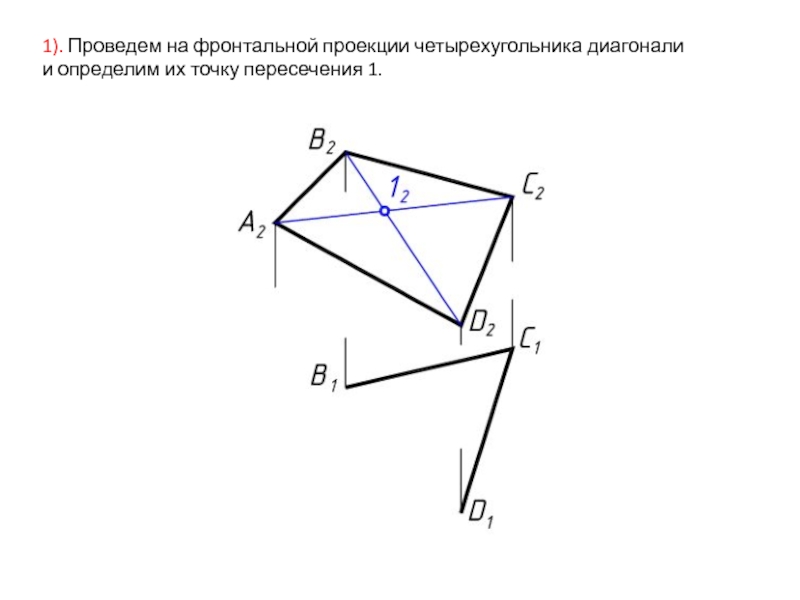
- 3. 1). Проведем на фронтальной проекции четырехугольника диагонали и определим их точку пересечения 1.
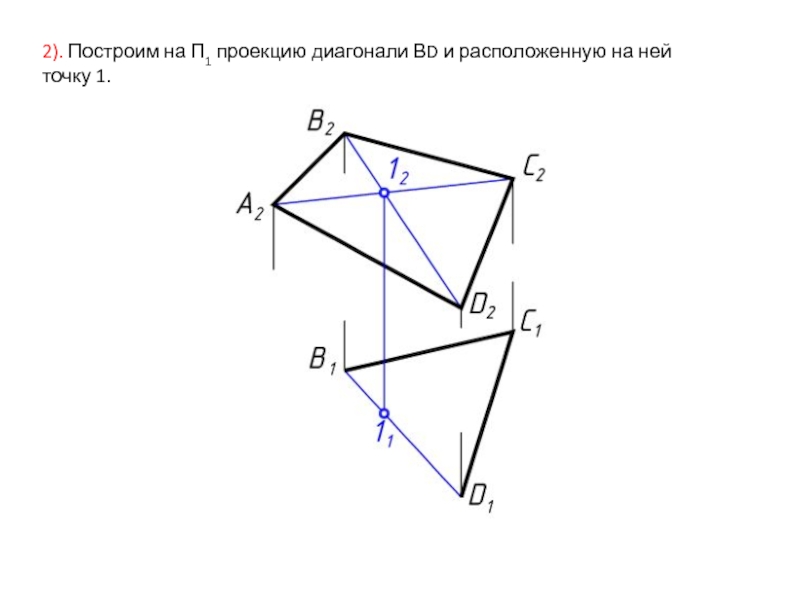
- 4. 2). Построим на П1 проекцию диагонали ВD и расположенную на ней точку 1.
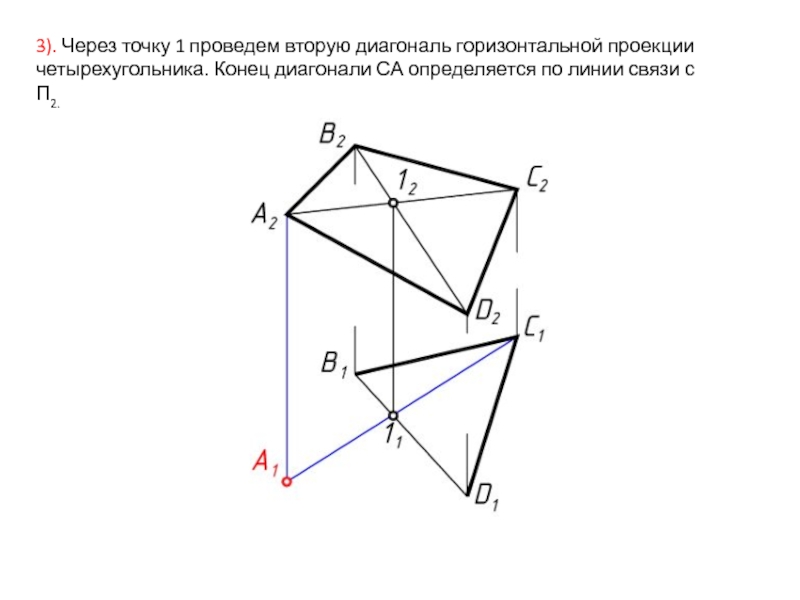
- 5. 3). Через точку 1 проведем вторую диагональ
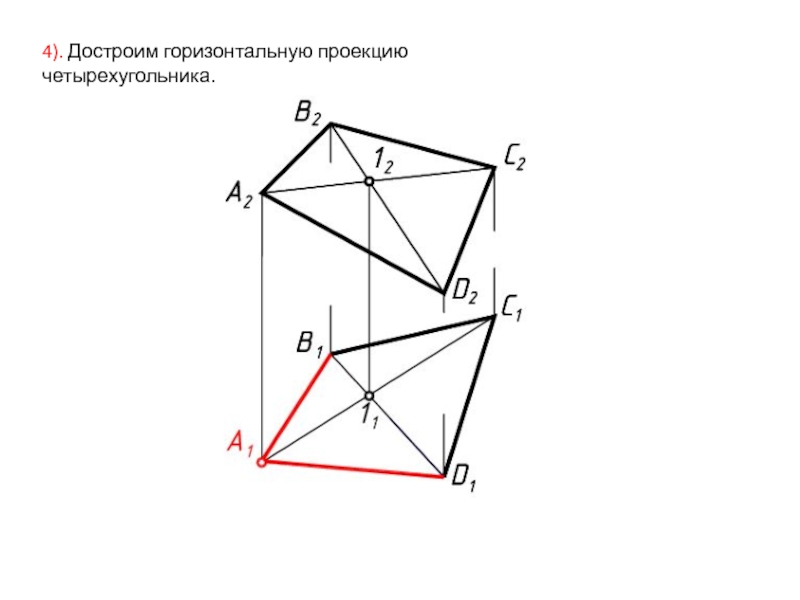
- 6. 4). Достроим горизонтальную проекцию четырехугольника.
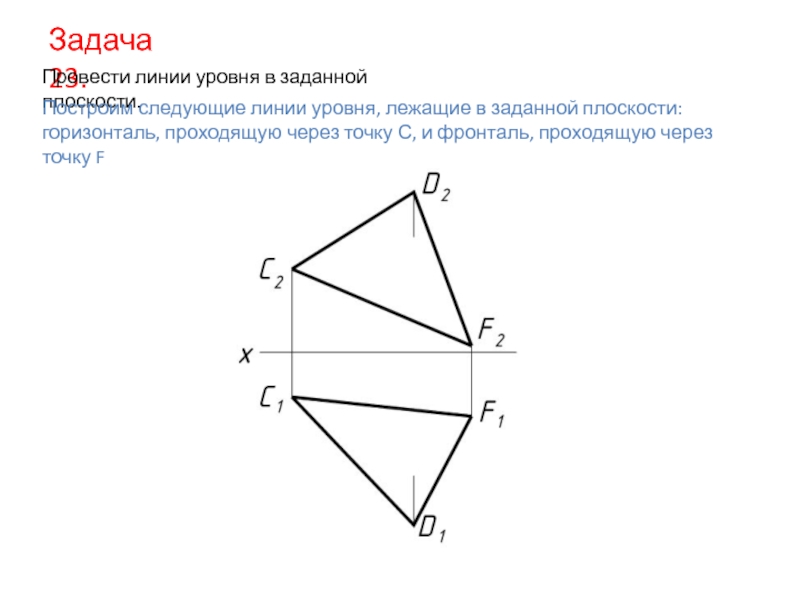
- 7. Задача 23. Провести линии уровня в заданной
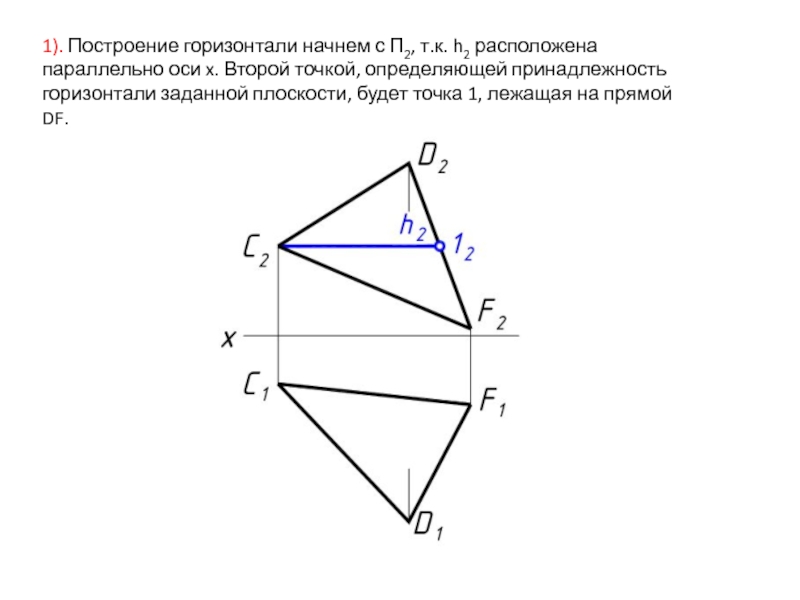
- 8. 1). Построение горизонтали начнем с П2, т.к.
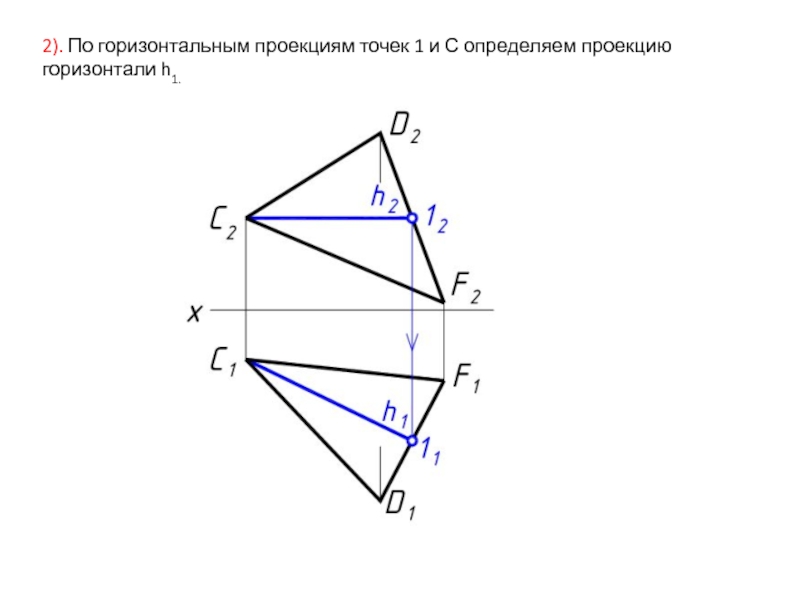
- 9. 2). По горизонтальным проекциям точек 1 и С определяем проекцию горизонтали h1.
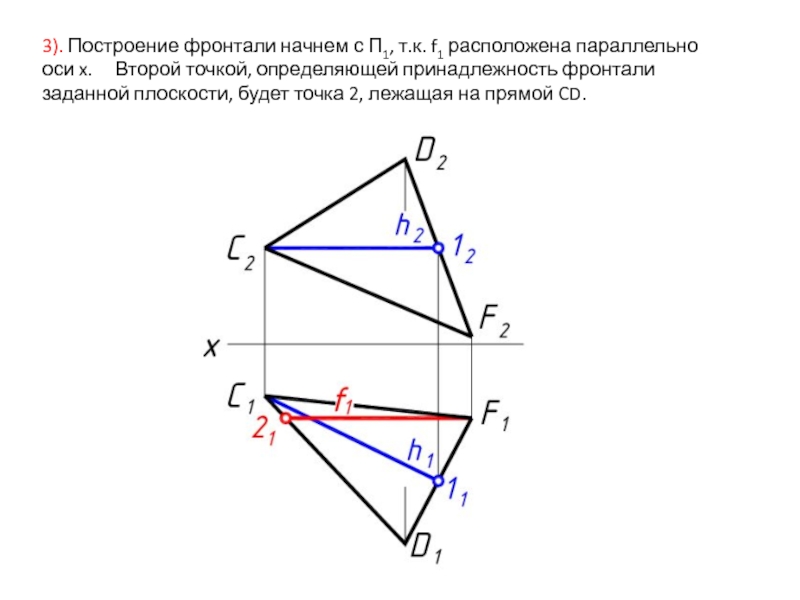
- 10. 3). Построение фронтали начнем с П1, т.к.
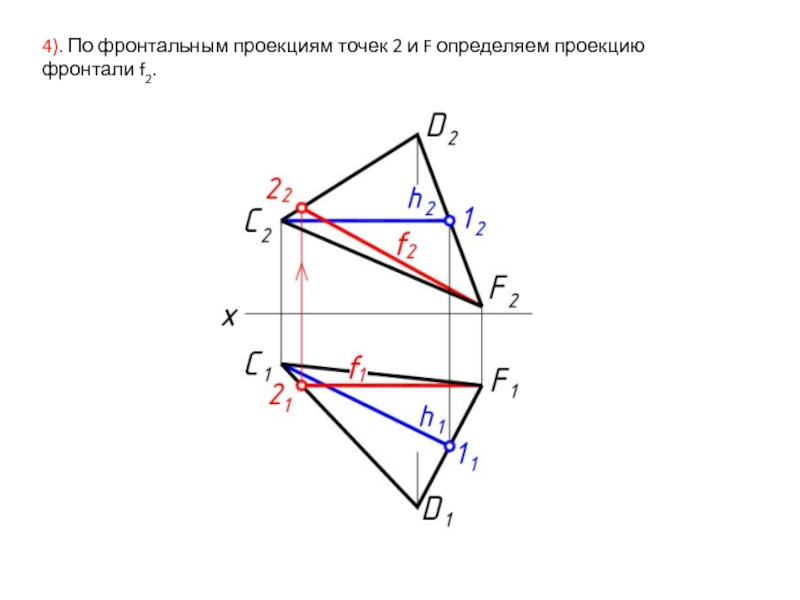
- 11. 4). По фронтальным проекциям точек 2 и F определяем проекцию фронтали f2.
- 12. Задача 24. В горизонтально-проецирующей плоскости Θ (Θ
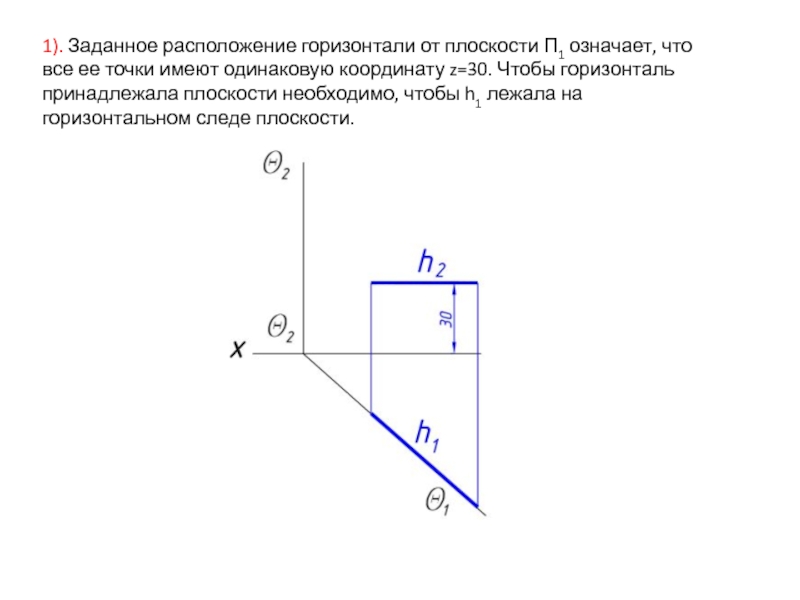
- 13. 1). Заданное расположение горизонтали от плоскости П1
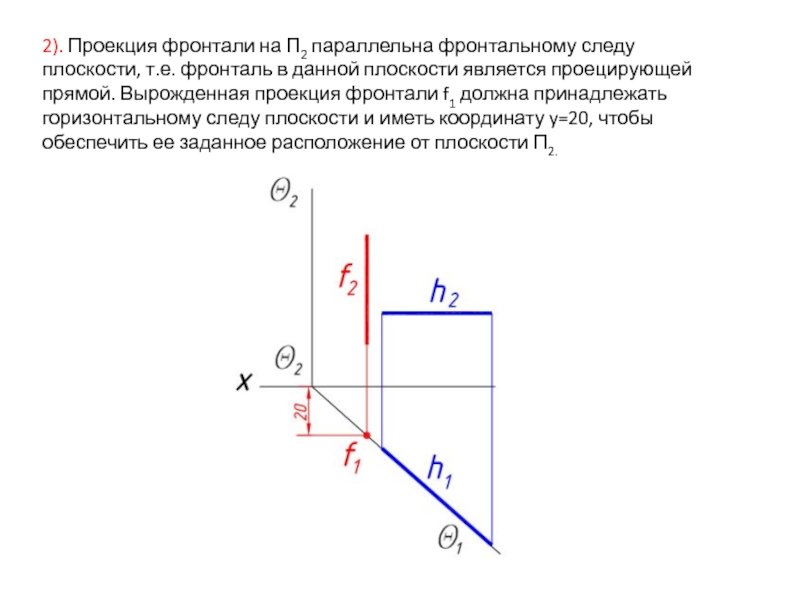
- 14. 2). Проекция фронтали на П2 параллельна фронтальному
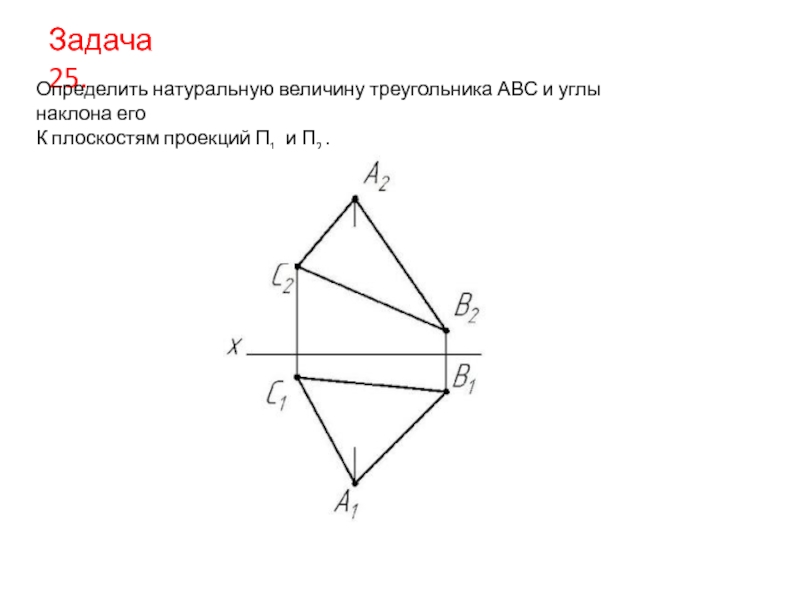
- 15. Задача 25. Определить натуральную величину треугольника АВС
- 16. 1). Для преобразования плоскости общего положения в
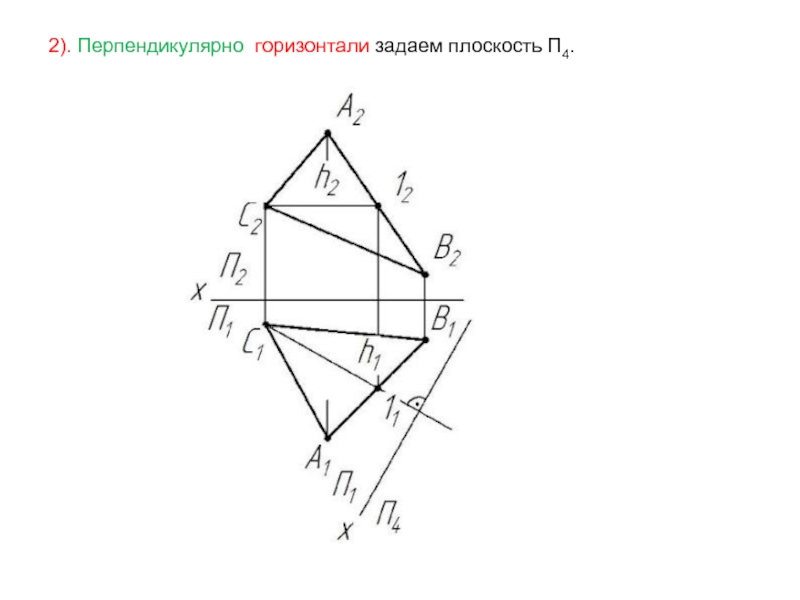
- 17. 2). Перпендикулярно горизонтали задаем плоскость П4.
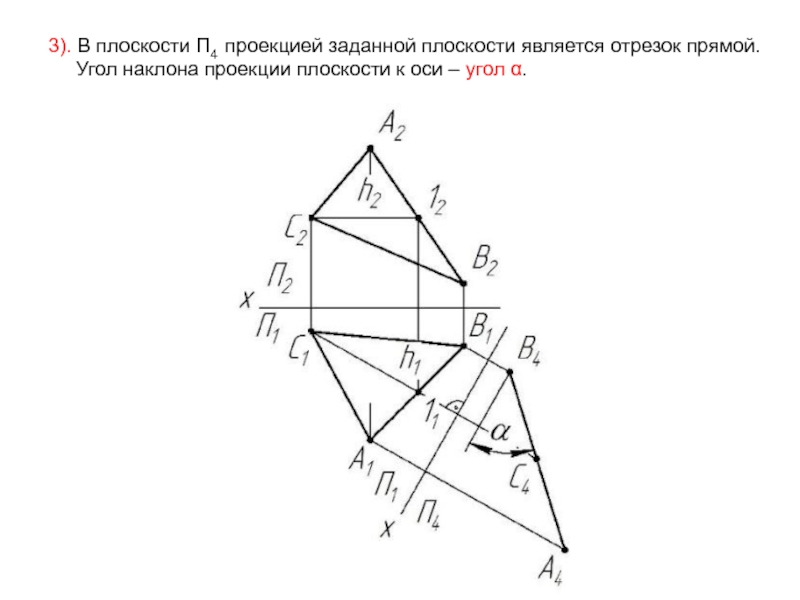
- 18. 3). В плоскости П4 проекцией заданной плоскости
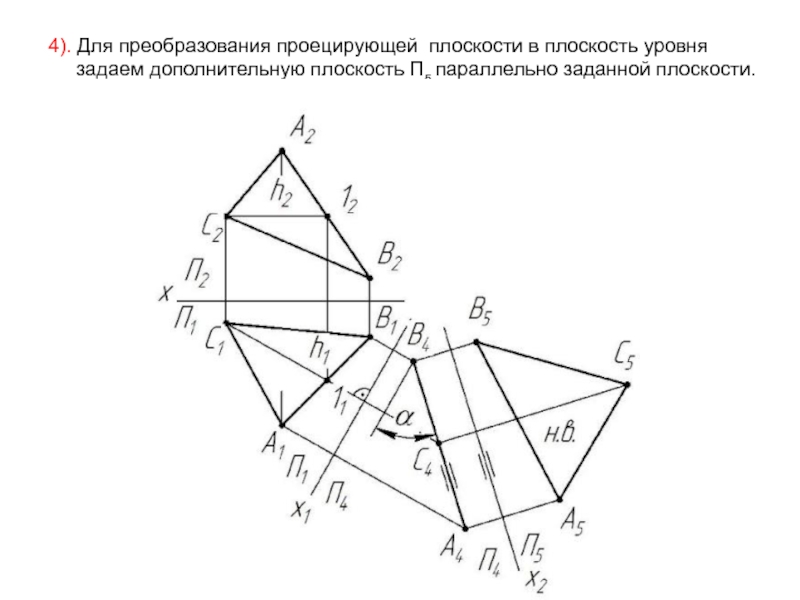
- 19. 4). Для преобразования проецирующей плоскости в плоскость
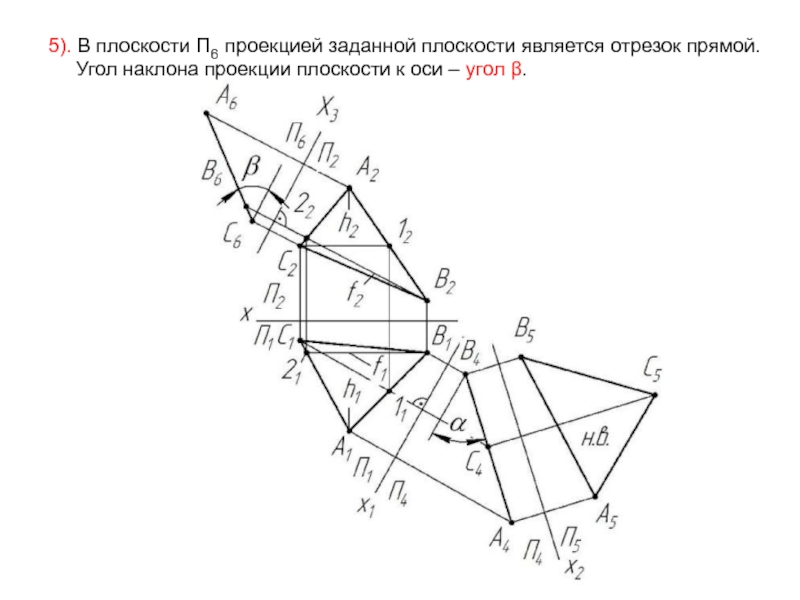
- 20. 5). В плоскости П6 проекцией заданной плоскости
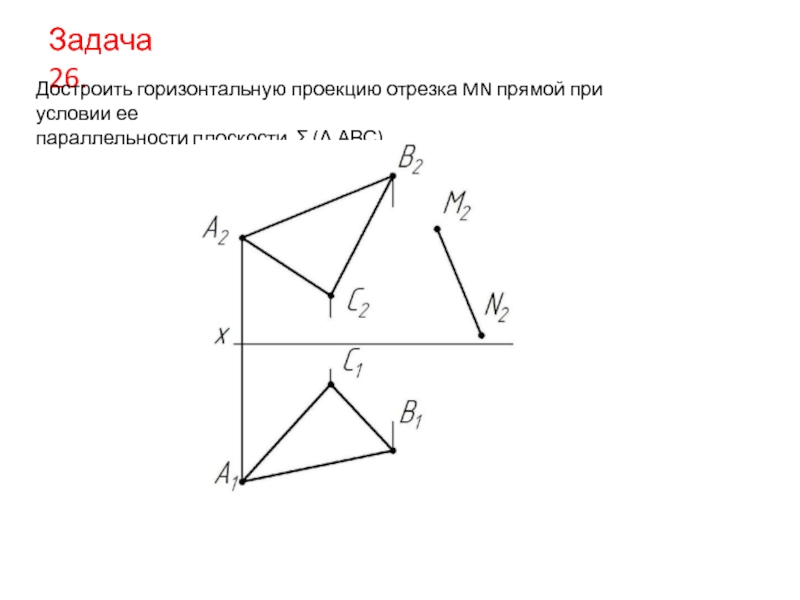
- 21. Задача 26. Достроить горизонтальную проекцию отрезка MN
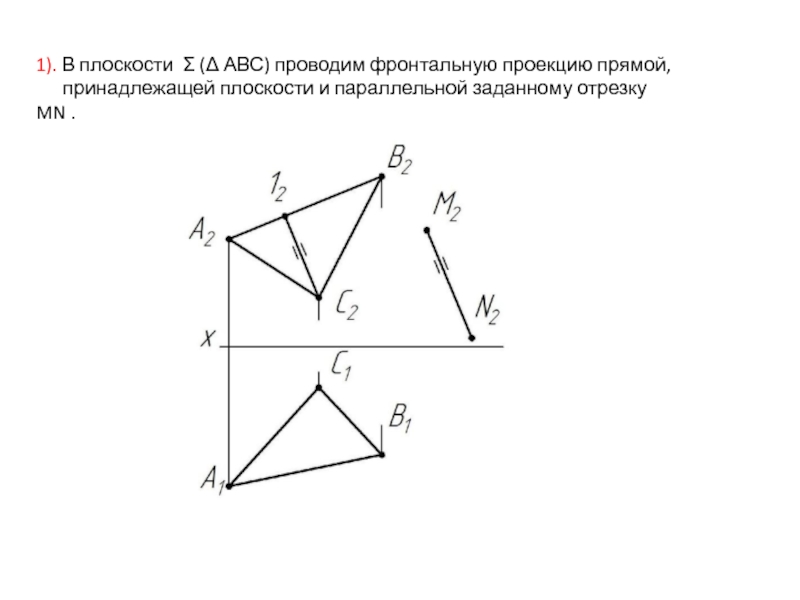
- 22. 1). В плоскости Σ (Δ АВС) проводим
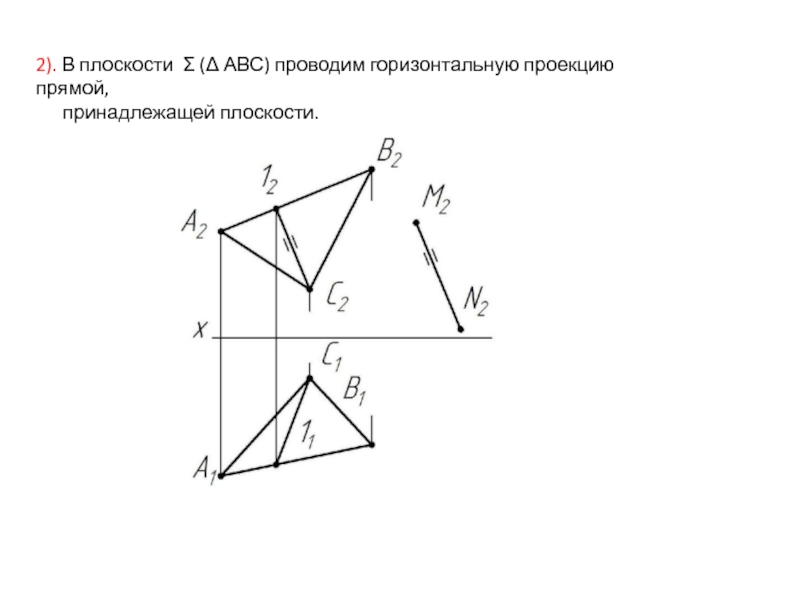
- 23. 2). В плоскости Σ (Δ АВС) проводим
- 24. 3). Выбираем одно из множества решений горизонтальной проекции отрезка MN .
- 25. Задача 27. Через точку M провести прямую
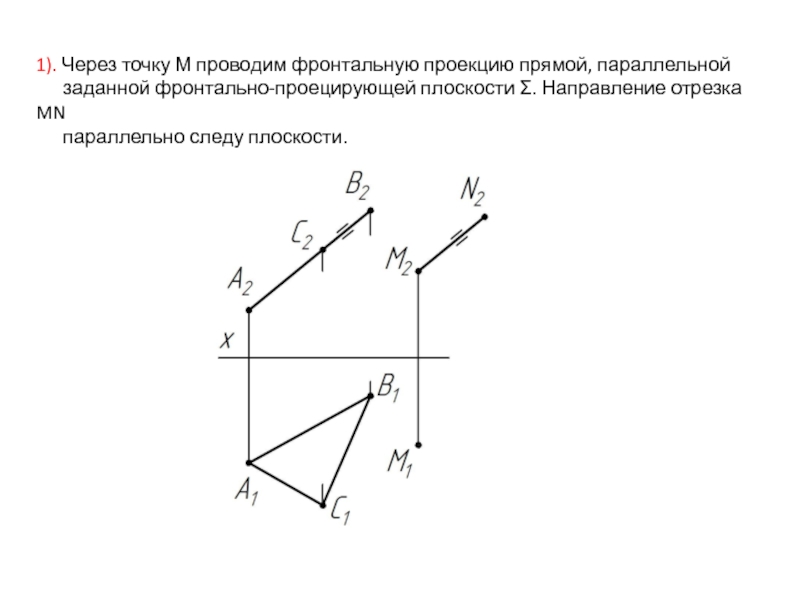
- 26. 1). Через точку М проводим фронтальную проекцию
- 27. 2). Выбираем одно из множества решений горизонтальной проекции отрезка MN .
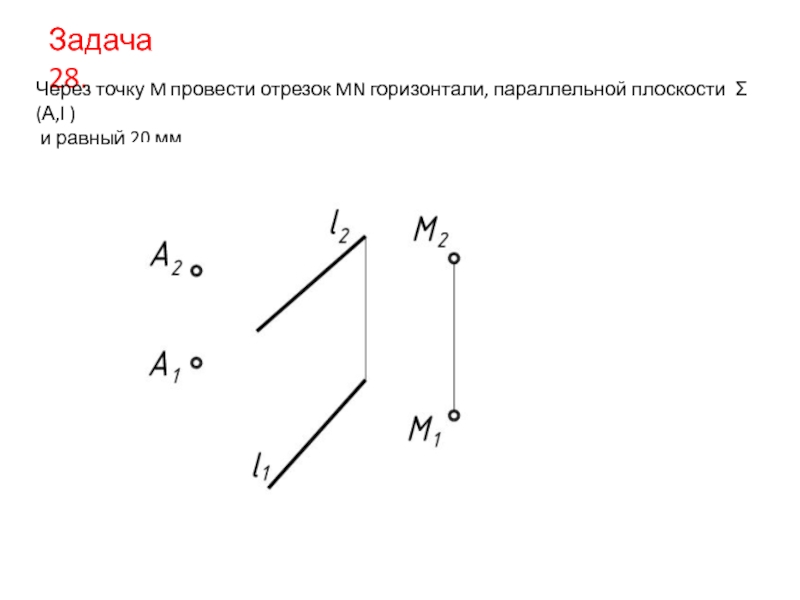
- 28. Задача 28. Через точку M провести отрезок
- 29. 1). Чтобы использовать признак параллельности прямой и
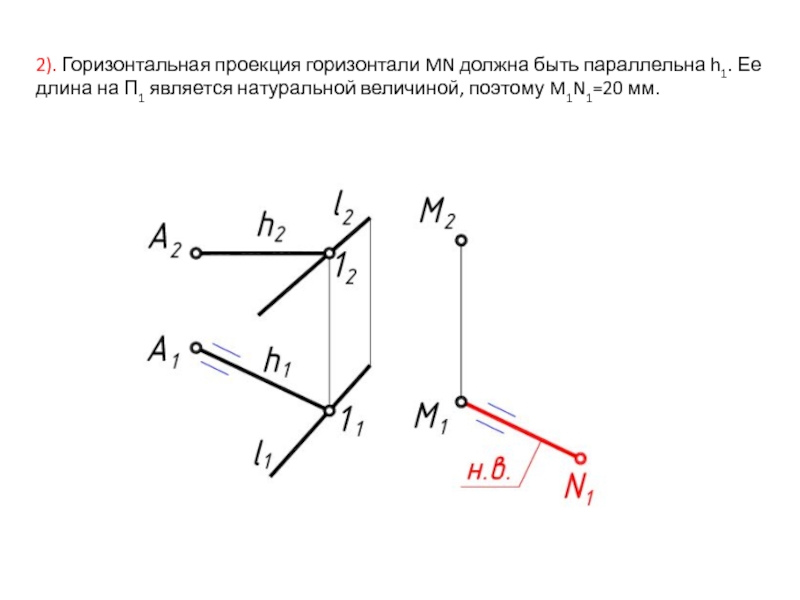
- 30. 2). Горизонтальная проекция горизонтали MN должна быть
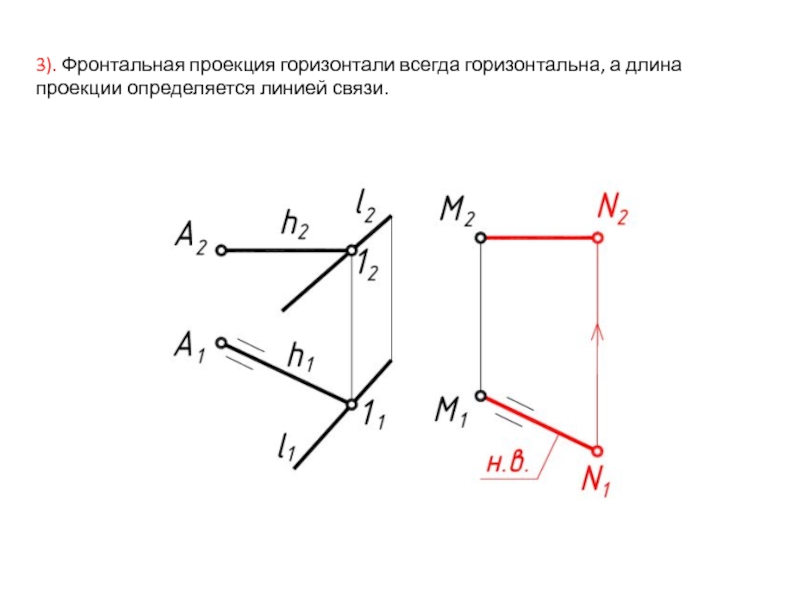
- 31. 3). Фронтальная проекция горизонтали всегда горизонтальна, а длина проекции определяется линией связи.
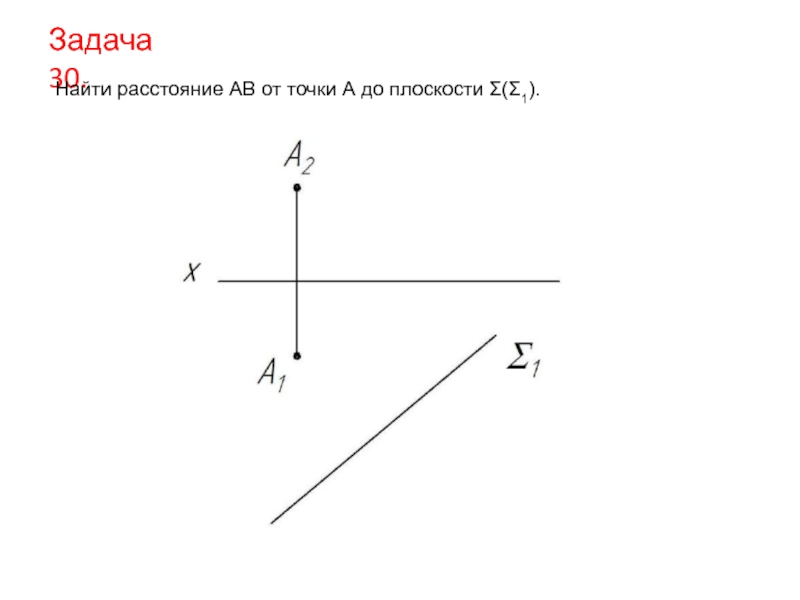
- 32. Задача 30. Найти расстояние AB от точки А до плоскости Σ(Σ1).
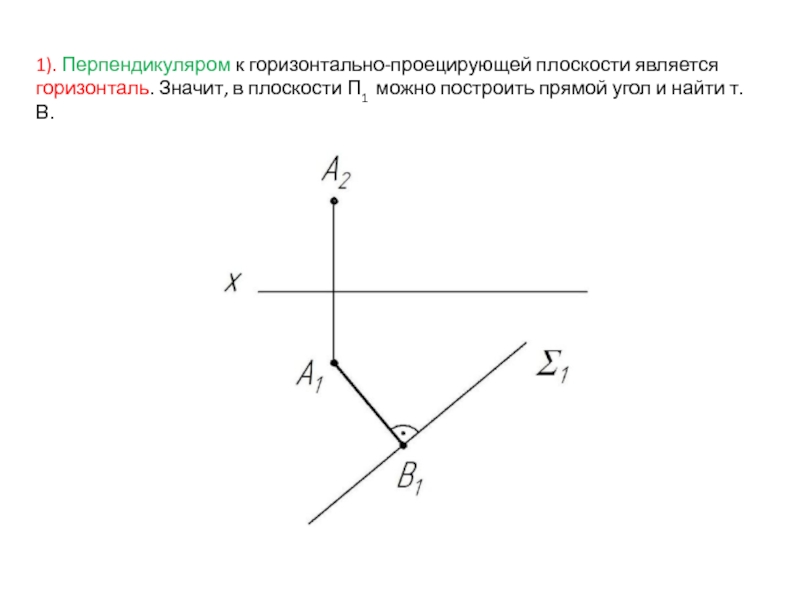
- 33. 1). Перпендикуляром к горизонтально-проецирующей плоскости является горизонталь.
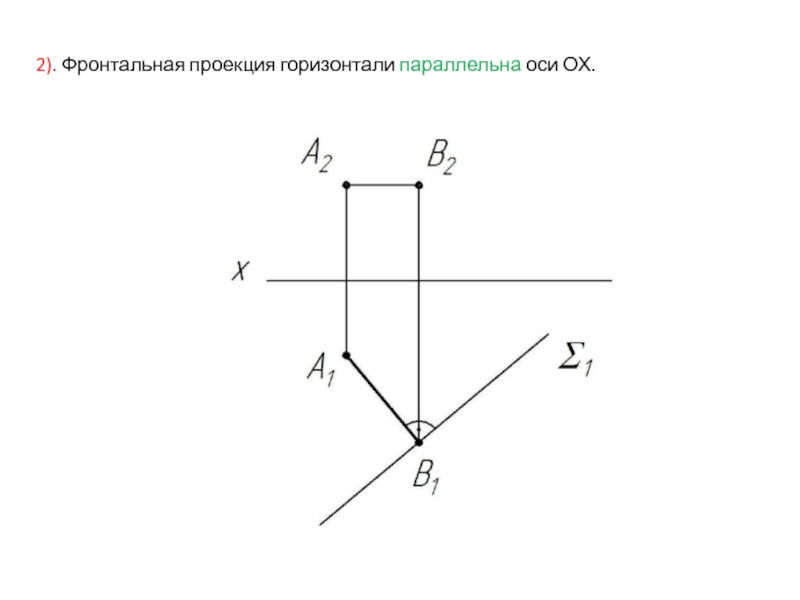
- 34. 2). Фронтальная проекция горизонтали параллельна оси ОХ.
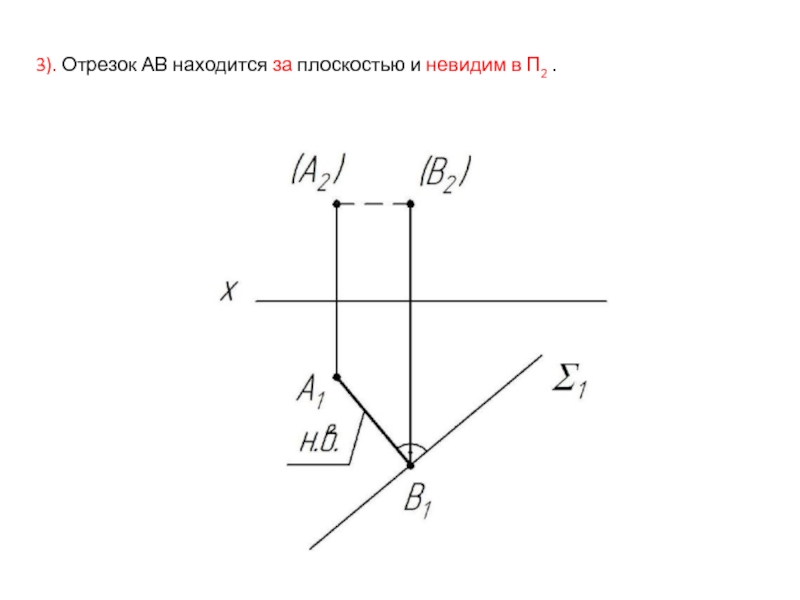
- 35. 3). Отрезок АВ находится за плоскостью и невидим в П2 .
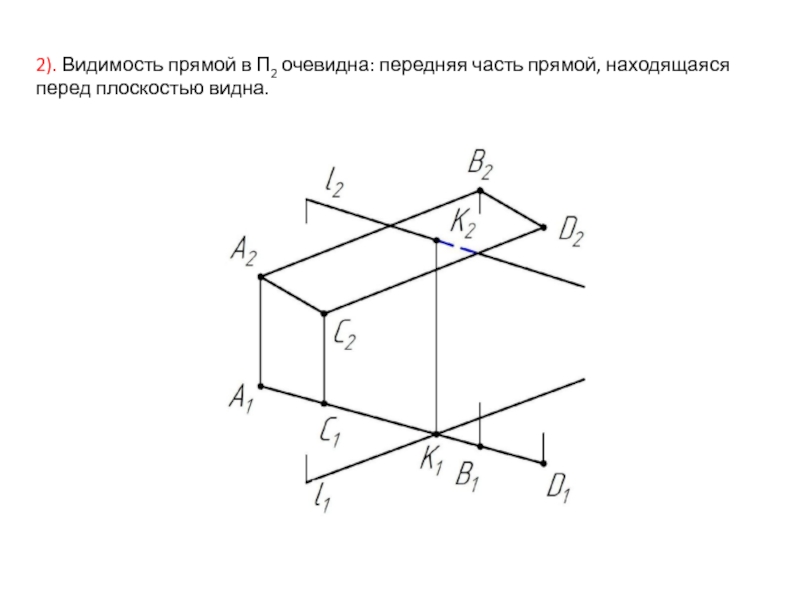
- 36. Задача 31. Построить точку пересечения прямой l с плоскостью Σ(ABCD). Показать видимость прямой.
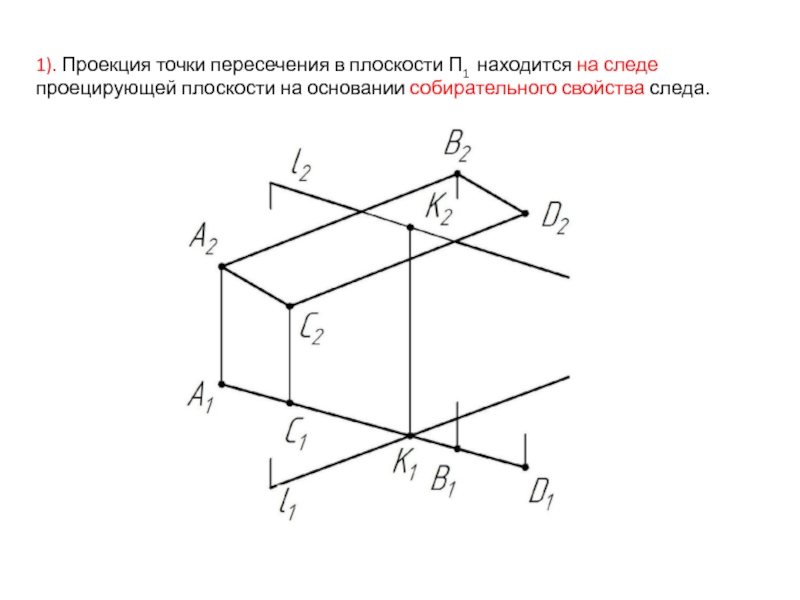
- 37. 1). Проекция точки пересечения в плоскости П1
- 38. 2). Видимость прямой в П2 очевидна: передняя часть прямой, находящаяся перед плоскостью видна.
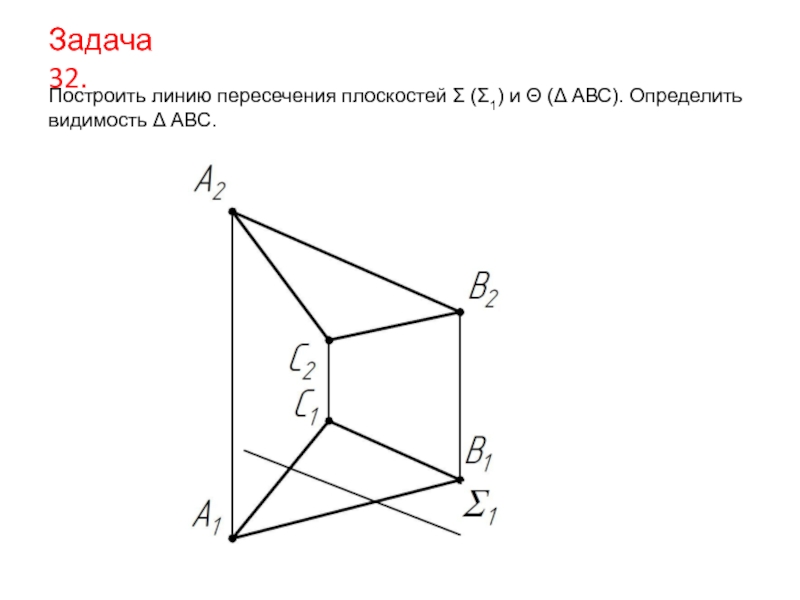
- 39. Задача 32. Построить линию пересечения плоскостей Σ
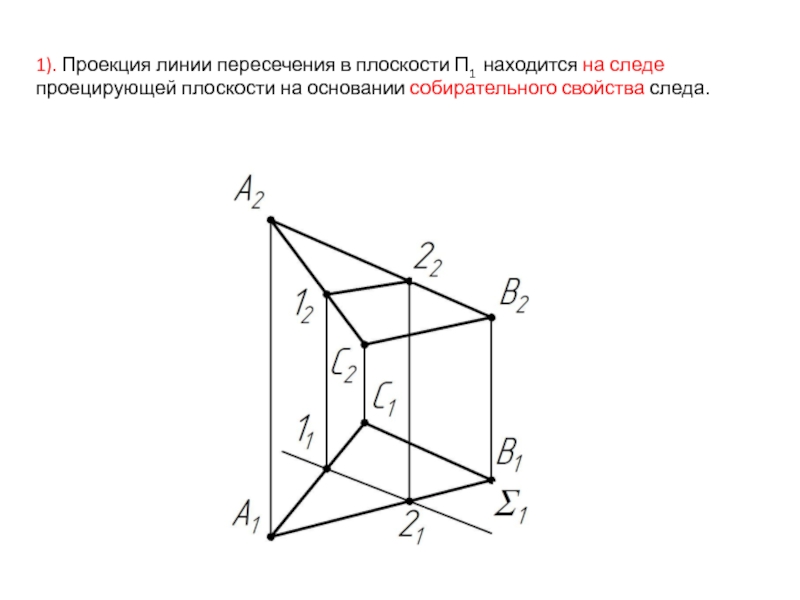
- 40. 1). Проекция линии пересечения в плоскости П1
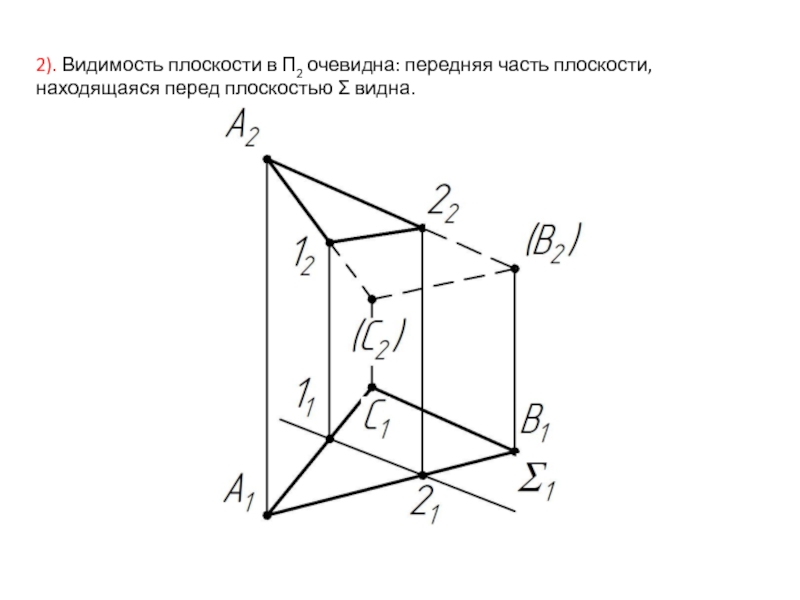
- 41. 2). Видимость плоскости в П2 очевидна: передняя часть плоскости, находящаяся перед плоскостью Σ видна.
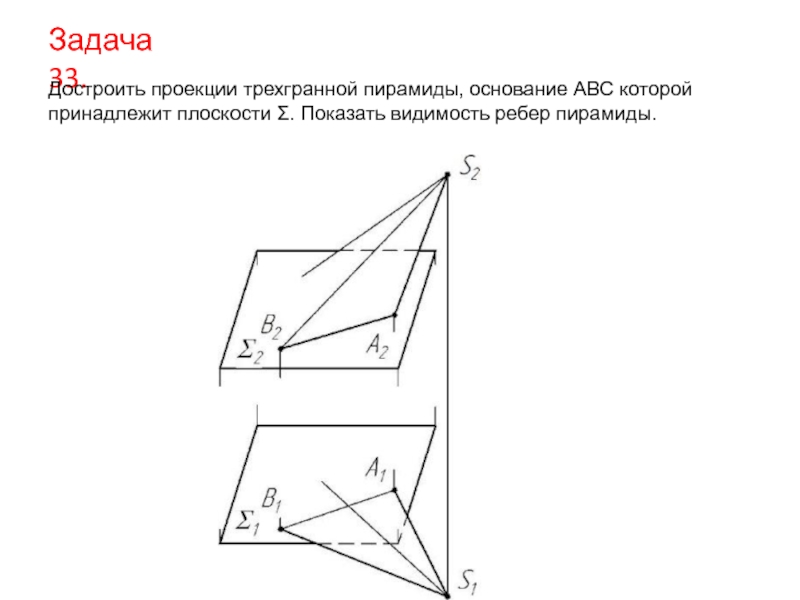
- 42. Задача 33. Достроить проекции трехгранной пирамиды, основание
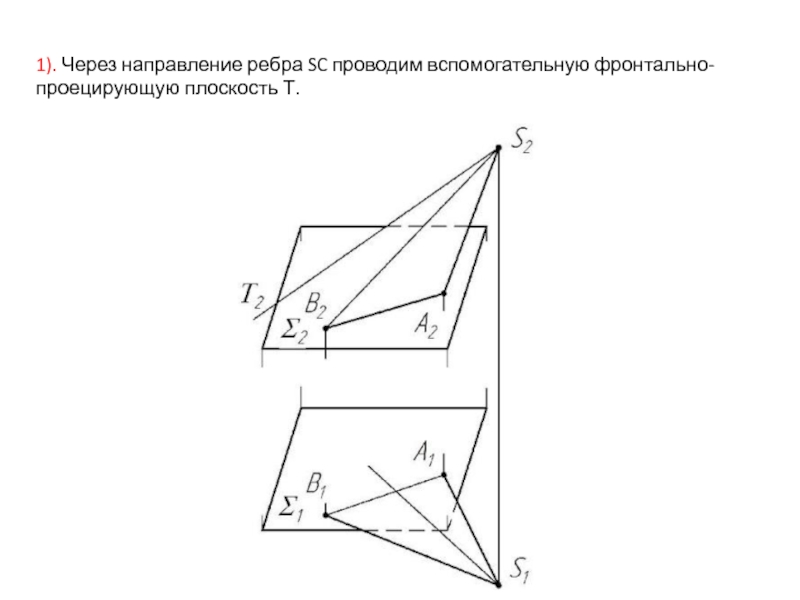
- 43. 1). Через направление ребра SC проводим вспомогательную фронтально-проецирующую плоскость Τ.
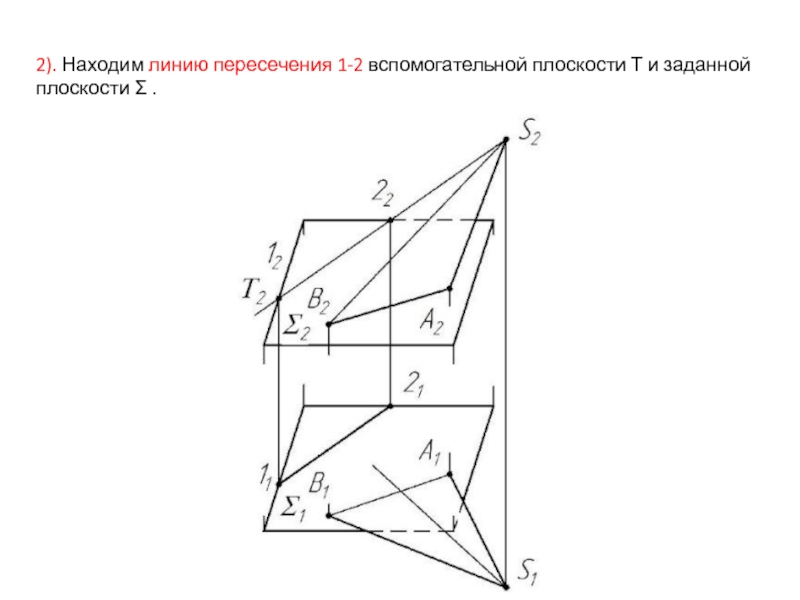
- 44. 2). Находим линию пересечения 1-2 вспомогательной плоскости Τ и заданной плоскости Σ .
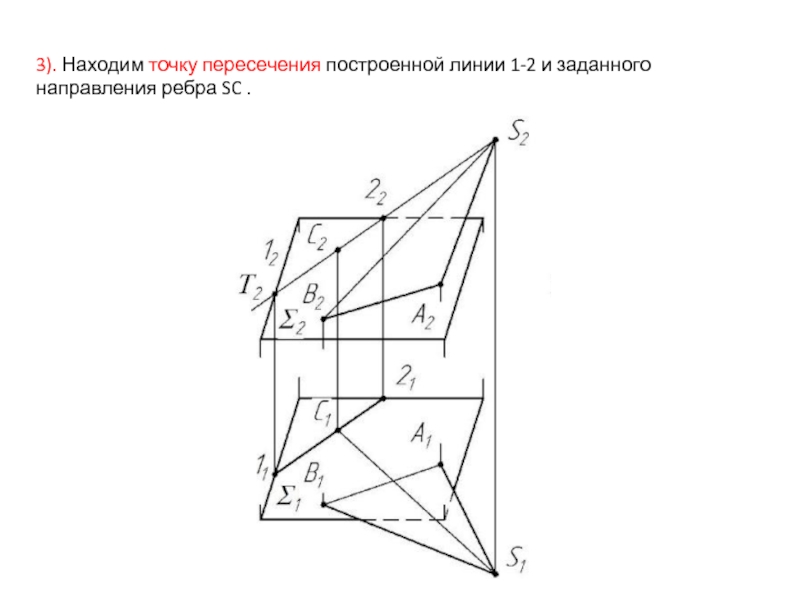
- 45. 3). Находим точку пересечения построенной линии 1-2 и заданного направления ребра SC .
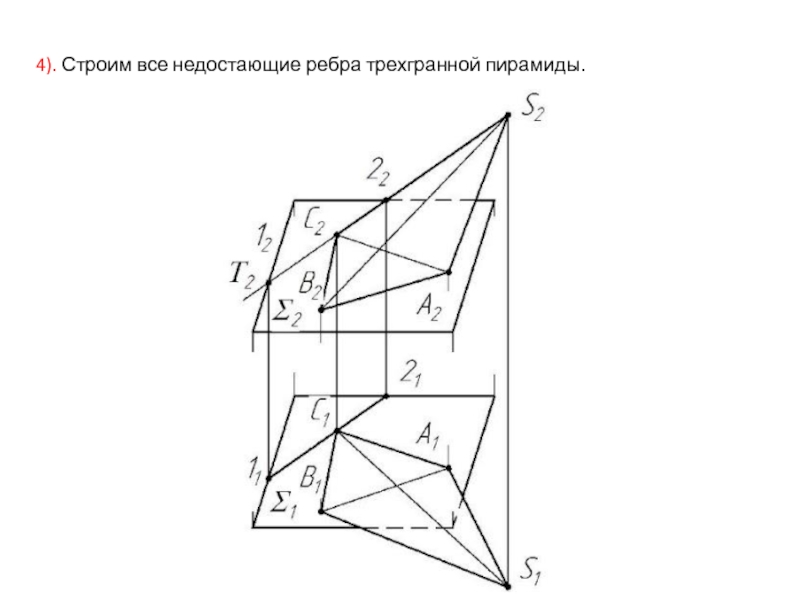
- 46. 4). Строим все недостающие ребра трехгранной пирамиды.
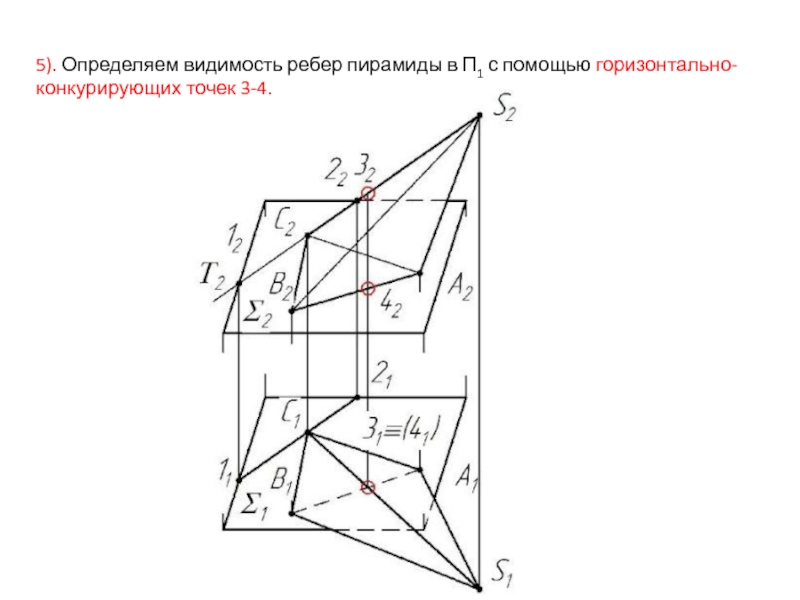
- 47. 5). Определяем видимость ребер пирамиды в П1 с помощью горизонтально-конкурирующих точек 3-4.
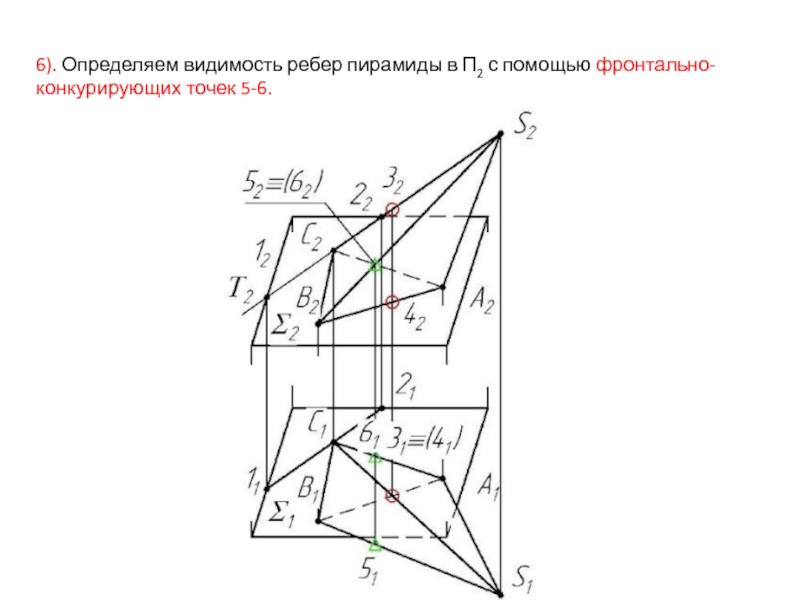
- 48. 6). Определяем видимость ребер пирамиды в П2 с помощью фронтально-конкурирующих точек 5-6.
Задача 22. Достроить горизонтальные проекции плоского многоугольника ABCD и прямой l, лежащей в его плоскости. Четырехугольник является плоской фигурой. Для построения его горизонтальной проекции необходимо использовать признаки принадлежности прямой и
Слайд 2Задача 22.
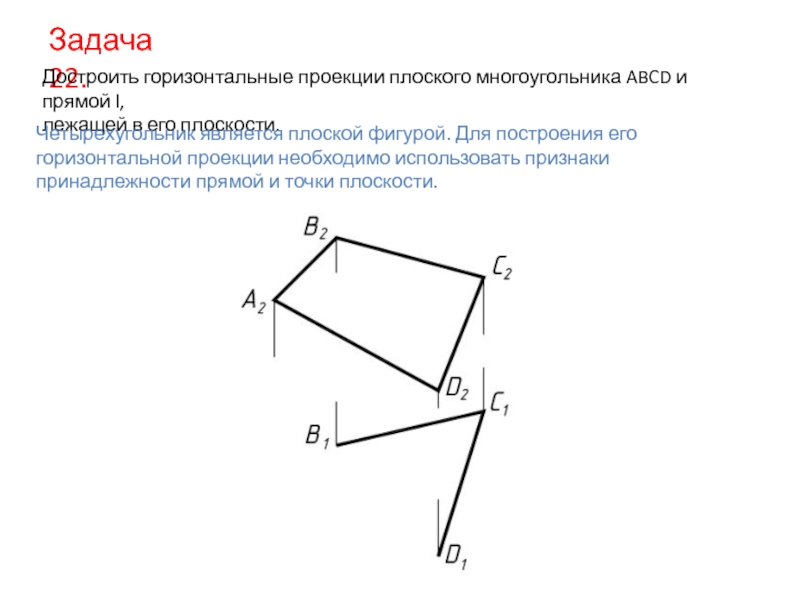
Достроить горизонтальные проекции плоского многоугольника ABCD и прямой l,
лежащей
в его плоскости.
Четырехугольник является плоской фигурой. Для построения его горизонтальной проекции необходимо использовать признаки принадлежности прямой и точки плоскости.
Слайд 31). Проведем на фронтальной проекции четырехугольника диагонали и определим их точку
пересечения 1.
Слайд 53). Через точку 1 проведем вторую диагональ горизонтальной проекции четырехугольника. Конец
диагонали СА определяется по линии связи с П2.
Слайд 7Задача 23.
Провести линии уровня в заданной плоскости.
Построим следующие линии уровня, лежащие
в заданной плоскости: горизонталь, проходящую через точку С, и фронталь, проходящую через точку F
Слайд 81). Построение горизонтали начнем с П2, т.к. h2 расположена параллельно оси
x. Второй точкой, определяющей принадлежность горизонтали заданной плоскости, будет точка 1, лежащая на прямой DF.
Слайд 103). Построение фронтали начнем с П1, т.к. f1 расположена параллельно оси
x. Второй точкой, определяющей принадлежность фронтали заданной плоскости, будет точка 2, лежащая на прямой CD.
Слайд 12Задача 24.
В горизонтально-проецирующей плоскости Θ (Θ 1,Θ2 ) провести горизонталь, удаленную
от П1 на 40 мм, и фронталь, удаленную от П2 на 15 мм.
Данная плоскость на П1 вырождается в прямую, поэтому горизонтальные проекции всех линий, лежащих в плоскости, должны совпадать с ее горизонтальным следом.
Слайд 131). Заданное расположение горизонтали от плоскости П1 означает, что все ее
точки имеют одинаковую координату z=30. Чтобы горизонталь принадлежала плоскости необходимо, чтобы h1 лежала на горизонтальном следе плоскости.
Слайд 142). Проекция фронтали на П2 параллельна фронтальному следу плоскости, т.е. фронталь
в данной плоскости является проецирующей прямой. Вырожденная проекция фронтали f1 должна принадлежать горизонтальному следу плоскости и иметь координату y=20, чтобы обеспечить ее заданное расположение от плоскости П2.
Слайд 15Задача 25.
Определить натуральную величину треугольника АВС и углы наклона его
К плоскостям
проекций П1 и П2 .
Слайд 161). Для преобразования плоскости общего положения в проецирующую
проводим горизонталь, принадлежащую этой плоскости.
Слайд 183). В плоскости П4 проекцией заданной плоскости является отрезок прямой.
Угол наклона проекции плоскости к оси – угол α.
Слайд 194). Для преобразования проецирующей плоскости в плоскость уровня
задаем дополнительную плоскость П5 параллельно заданной плоскости.
Слайд 205). В плоскости П6 проекцией заданной плоскости является отрезок прямой.
Угол наклона проекции плоскости к оси – угол β.
Слайд 21Задача 26.
Достроить горизонтальную проекцию отрезка MN прямой при условии ее
параллельности
плоскости Σ (Δ АВС).
Слайд 221). В плоскости Σ (Δ АВС) проводим фронтальную проекцию прямой,
принадлежащей плоскости и параллельной заданному отрезку MN .
Слайд 261). Через точку М проводим фронтальную проекцию прямой, параллельной
заданной фронтально-проецирующей плоскости Σ. Направление отрезка MN
параллельно следу плоскости.
параллельно следу плоскости.
Слайд 28Задача 28.
Через точку M провести отрезок MN горизонтали, параллельной плоскости Σ
(А,l )
и равный 20 мм.
и равный 20 мм.
Слайд 291). Чтобы использовать признак параллельности прямой и плоскости, в данной задаче
необходимо в плоскости иметь горизонталь. Выполним построение горизонтали А-1, принадлежащей заданной плоскости.
Слайд 302). Горизонтальная проекция горизонтали MN должна быть параллельна h1. Ее
длина на П1 является натуральной величиной, поэтому M1N1=20 мм.
Слайд 313). Фронтальная проекция горизонтали всегда горизонтальна, а длина проекции определяется линией
связи.
Слайд 331). Перпендикуляром к горизонтально-проецирующей плоскости является горизонталь. Значит, в плоскости П1
можно построить прямой угол и найти т.В.
Слайд 36Задача 31.
Построить точку пересечения прямой l с плоскостью Σ(ABCD). Показать
видимость прямой.
Слайд 371). Проекция точки пересечения в плоскости П1 находится на следе проецирующей
плоскости на основании собирательного свойства следа.
Слайд 382). Видимость прямой в П2 очевидна: передняя часть прямой, находящаяся перед
плоскостью видна.
Слайд 39Задача 32.
Построить линию пересечения плоскостей Σ (Σ1) и Θ (Δ АВС).
Определить
видимость Δ АВС.
видимость Δ АВС.
Слайд 401). Проекция линии пересечения в плоскости П1 находится на следе проецирующей
плоскости на основании собирательного свойства следа.
Слайд 412). Видимость плоскости в П2 очевидна: передняя часть плоскости, находящаяся перед
плоскостью Σ видна.
Слайд 42Задача 33.
Достроить проекции трехгранной пирамиды, основание АВС которой
принадлежит плоскости Σ. Показать
видимость ребер пирамиды.
Слайд 431). Через направление ребра SC проводим вспомогательную фронтально-проецирующую плоскость Τ.
Слайд 475). Определяем видимость ребер пирамиды в П1 с помощью горизонтально-конкурирующих точек
3-4.
