- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Взаимное расположение прямых и плоскостей, двух плоскостей презентация
Содержание
- 1. Взаимное расположение прямых и плоскостей, двух плоскостей
- 2. Прямая и точка в плоскости
- 3. Главные линии плоскости х А2 В2
- 4. Прямая, параллельная плоскости Прямая параллельна
- 5. Параллельные плоскости Две плоскости параллельны,
- 6. Прямая, перпендикулярная плоскости A
- 7. Построение взаимно перпендикулярных плоскостей основано на
Слайд 2
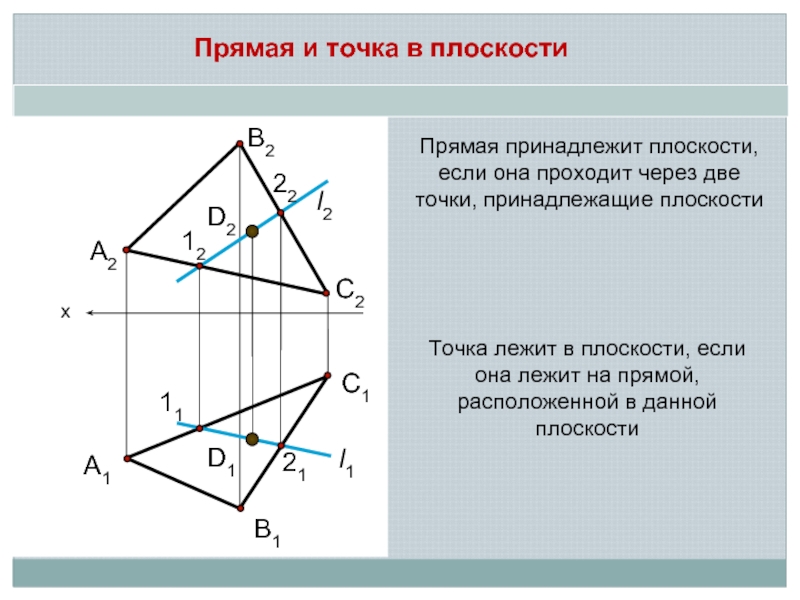
Прямая и точка в плоскости
х
А2
В2
С2
С1
А1
В1
l2
l1
12
22
11
21
D2
D1
Прямая принадлежит плоскости, если она проходит через
Точка лежит в плоскости, если она лежит на прямой, расположенной в данной плоскости
Слайд 3
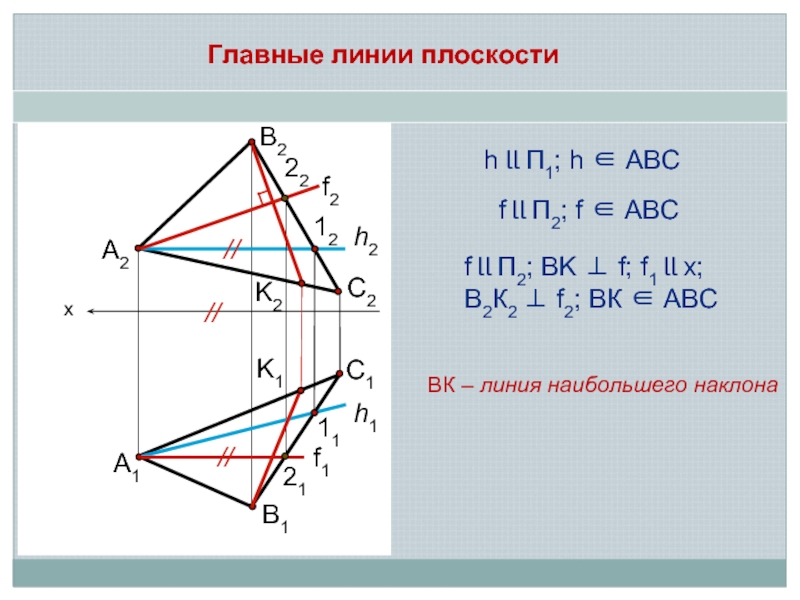
Главные линии плоскости
х
А2
В2
С2
С1
А1
В1
h2
h1
12
22
11
21
f2
f1
h ll П1; h ∈ ABC
K2
K1
f ll П2; BK
ВК – линия наибольшего наклона
f ll П2; f ∈ ABC
//
//
//
Слайд 4
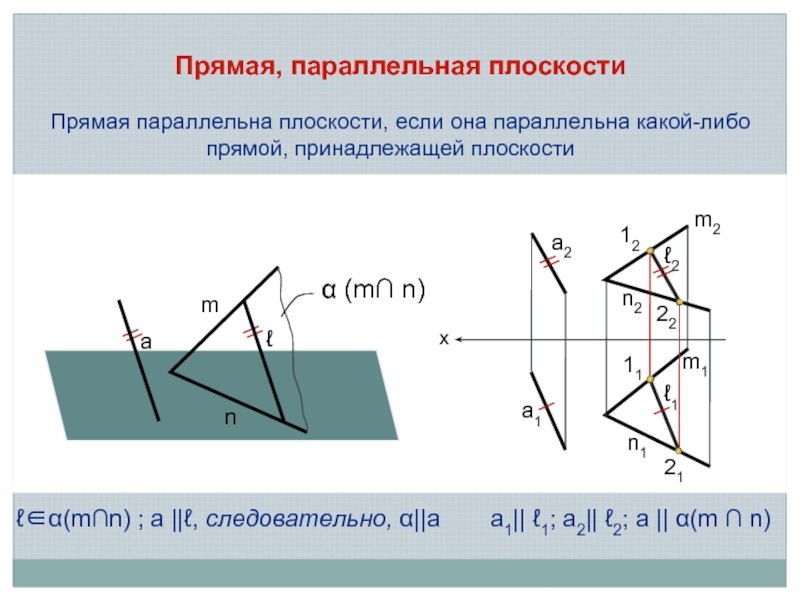
Прямая, параллельная плоскости
Прямая параллельна плоскости, если она параллельна какой-либо прямой, принадлежащей
ℓ∈α(m∩n) ; а ||ℓ, следовательно, α||а
а1|| ℓ1; а2|| ℓ2; а || α(m ∩ n)
х
a2
a1
m2
m1
n1
n2
ℓ2
ℓ1
//
//
/
/
12
11
22
21
a
m
n
ℓ
//
//
α (m∩ n)
Слайд 5
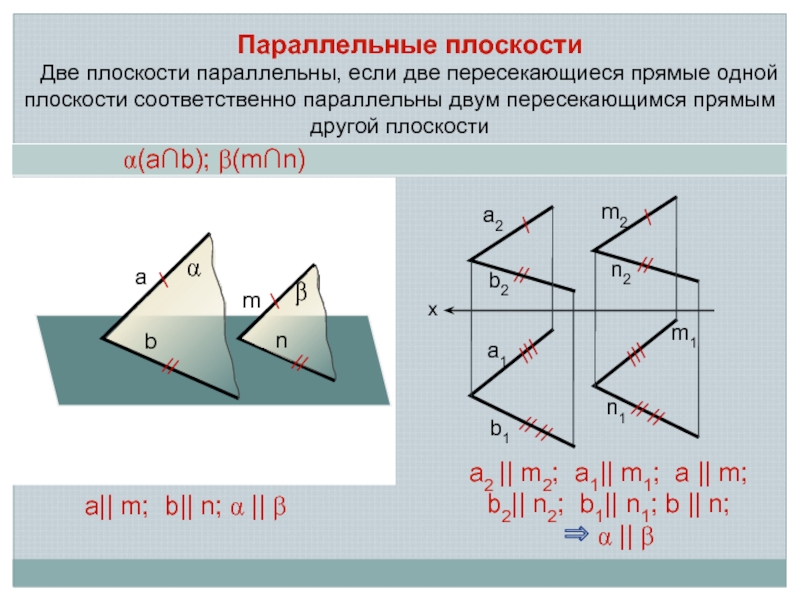
Параллельные плоскости
Две плоскости параллельны, если две пересекающиеся прямые одной плоскости соответственно
а2 || m2; a1|| m1; a || m;
b2|| n2; b1|| n1; b || n;
⇒ α || β
х
a2
a1
m2
m1
n1
n2
//
/
// //
a
//
β
α
//
/
/
b1
b2
///
//
/
// //
///
α(а∩b); β(m∩n)
а|| m; b|| n; α || β
b
n
m
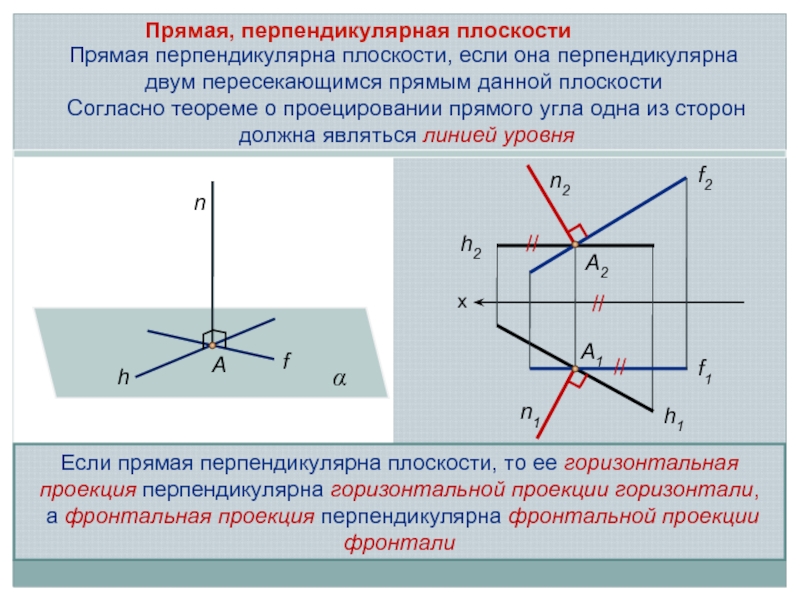
Слайд 6Прямая, перпендикулярная плоскости
A
α
n
f
h
х
h2
h1
f1
f2
A2
A1
n2
n1
Cогласно теореме о проецировании прямого угла одна из сторон
Если прямая перпендикулярна плоскости, то ее горизонтальная проекция перпендикулярна горизонтальной проекции горизонтали,
а фронтальная проекция перпендикулярна фронтальной проекции фронтали
Прямая перпендикулярна плоскости, если она перпендикулярна двум пересекающимся прямым данной плоскости
//
//
//
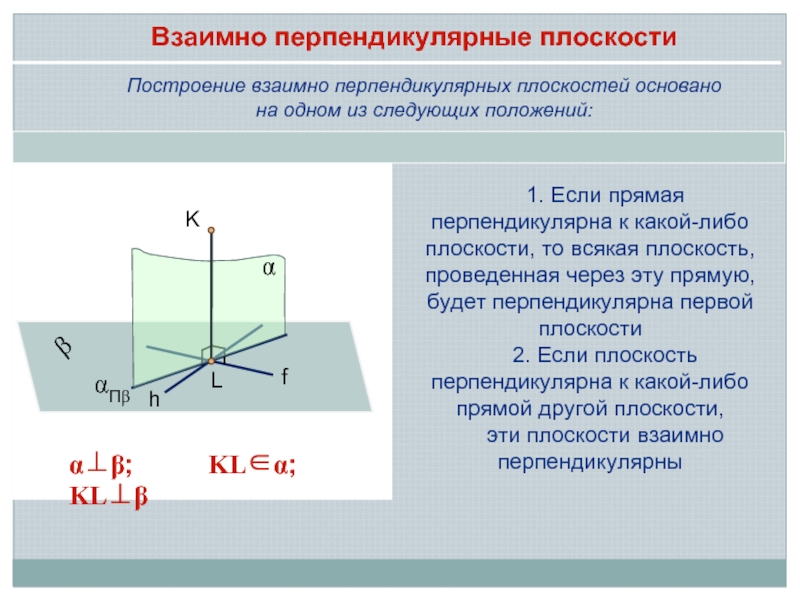
Слайд 7Построение взаимно перпендикулярных плоскостей основано
на одном из следующих положений:
1. Если
2. Если плоскость перпендикулярна к какой-либо прямой другой плоскости,
эти плоскости взаимно перпендикулярны
L
K
f
h
α
β
αПβ
Взаимно перпендикулярные плоскости
α⊥β; KL∈α; KL⊥β