- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Взаимное расположение двух прямых презентация
Содержание
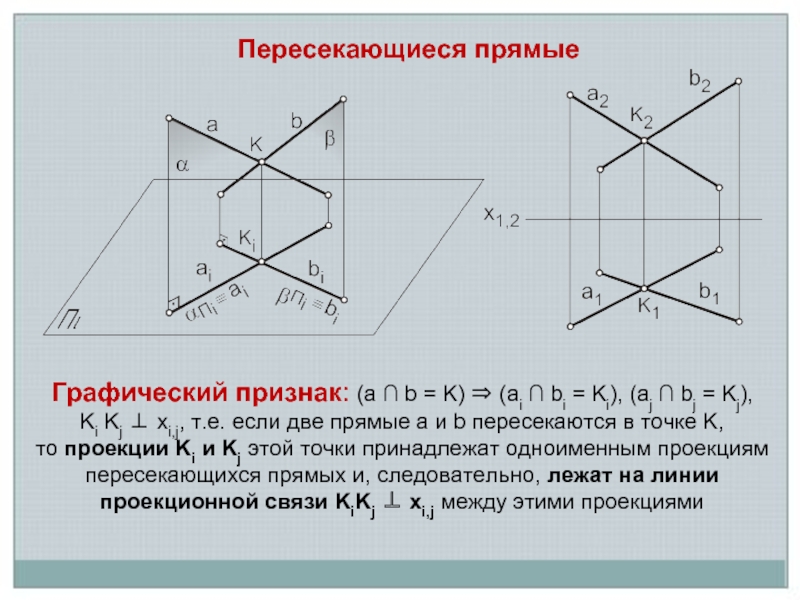
Слайд 2Пересекающиеся прямые
Графический признак: (a ∩ b = K) ⇒ (ai ∩
bi = Ki), (aj ∩ bj = Kj),
Ki Kj ⊥ xi,j, т.е. если две прямые a и b пересекаются в точке K,
то проекции Ki и Kj этой точки принадлежат одноименным проекциям пересекающихся прямых и, следовательно, лежат на линии проекционной связи KiKj ⊥ xi,j между этими проекциями
Ki Kj ⊥ xi,j, т.е. если две прямые a и b пересекаются в точке K,
то проекции Ki и Kj этой точки принадлежат одноименным проекциям пересекающихся прямых и, следовательно, лежат на линии проекционной связи KiKj ⊥ xi,j между этими проекциями
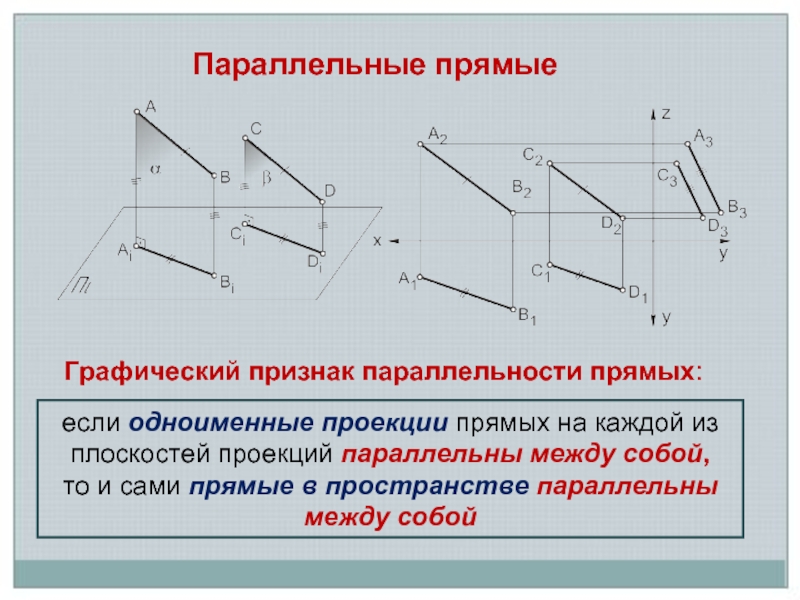
Слайд 3если одноименные проекции прямых на каждой из плоскостей проекций параллельны между
собой,
то и сами прямые в пространстве параллельны между собой
то и сами прямые в пространстве параллельны между собой
Графический признак параллельности прямых:
Параллельные прямые
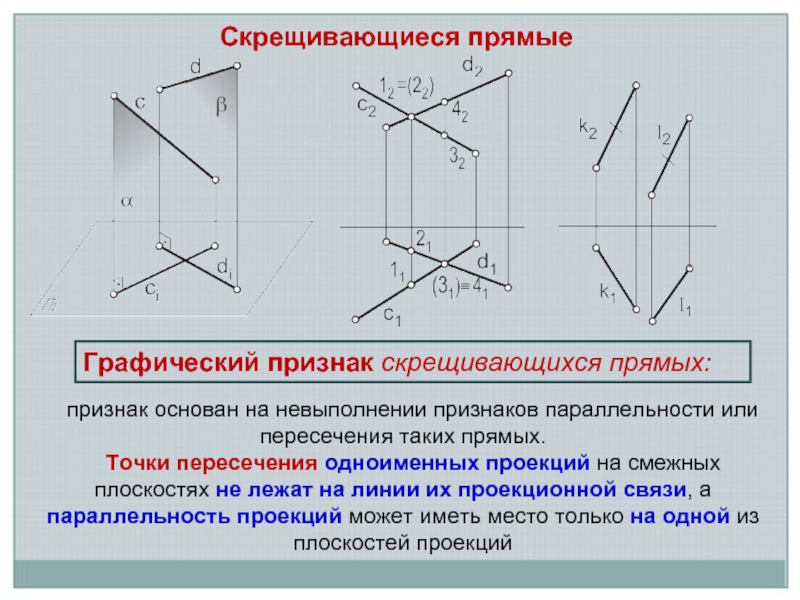
Слайд 4Скрещивающиеся прямые
Графический признак скрещивающихся прямых:
признак основан на невыполнении признаков
параллельности или пересечения таких прямых.
Точки пересечения одноименных проекций на смежных плоскостях не лежат на линии их проекционной связи, а параллельность проекций может иметь место только на одной из плоскостей проекций
Точки пересечения одноименных проекций на смежных плоскостях не лежат на линии их проекционной связи, а параллельность проекций может иметь место только на одной из плоскостей проекций
Слайд 5
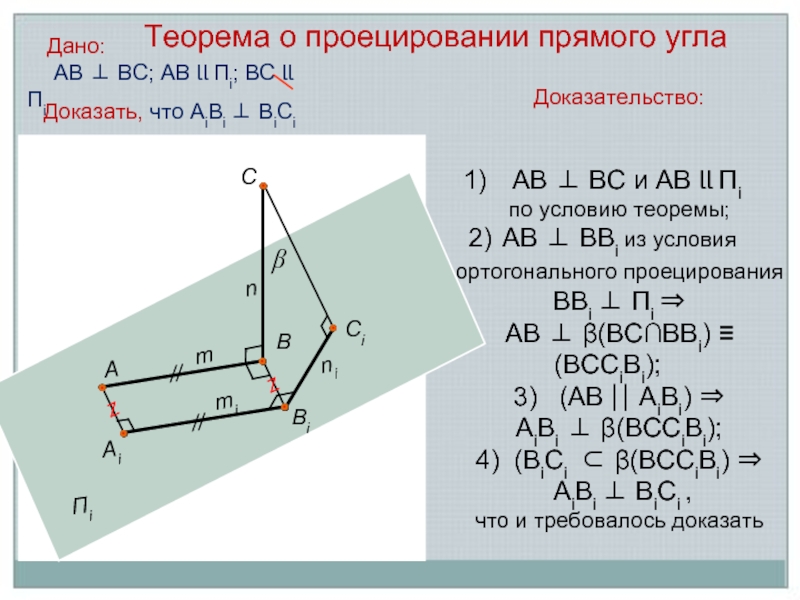
Дано:
АВ ⊥ ВС; АВ ll Пi; ВС ll Пi
Доказательство:
АВ
⊥ ВС и АВ ll Пi
по условию теоремы;
АВ ⊥ ВВi из условия ортогонального проецирования ВВi ⊥ Пi ⇒
АВ ⊥ β(ВС∩ВВi) ≡ (ВССiВi);
3) (АВ ⎢⎢ АiВi) ⇒
АiВi ⊥ β(ВССiВi);
4) (ВiСi ⊂ β(ВССiВi) ⇒
АiВi ⊥ ВiСi ,
что и требовалось доказать
по условию теоремы;
АВ ⊥ ВВi из условия ортогонального проецирования ВВi ⊥ Пi ⇒
АВ ⊥ β(ВС∩ВВi) ≡ (ВССiВi);
3) (АВ ⎢⎢ АiВi) ⇒
АiВi ⊥ β(ВССiВi);
4) (ВiСi ⊂ β(ВССiВi) ⇒
АiВi ⊥ ВiСi ,
что и требовалось доказать
С
Аi
А
Вi
В
Сi
//
//
Z
Z
mi
m
n
ni
Пi
Доказать, что АiВi ⊥ ВiСi
β
Теорема о проецировании прямого угла