- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Взаимное пересечение поверхностей вращения презентация
Содержание
Слайд 2
Линия пересечения распадается на
Полное (проницание) – все образующие одной поверхности пересекаются со второй поверхностью.
Частичное (врезание)– часть образующих одной поверхности пересекается частью образующих другой. Линия пересечения –замкнутая пространственная кривая
Слайд 3Теорема 1
Если две поверхности пересекаются по одной плоской кривой, то существует
Слайд 5– пересекающиеся криволинейные поверхности имеют
в одной точке общую плоскость касания
Одностороннее
Линия пересечения – замкнутая пространственная кривая, пересекающаяся сама с собой
в точке касания (точка самопересечения)
Слайд 6 Двойное соприкасание – пересекающиеся криволинейные поверхности имеют две общие касательные
В пересечении участвуют все образующие одной поверхности и все образующие второй
Слайд 7
M
N
Если две поверхности имеют касание в двух точках M и N,
Теорема (о двойном касании)
Слайд 10
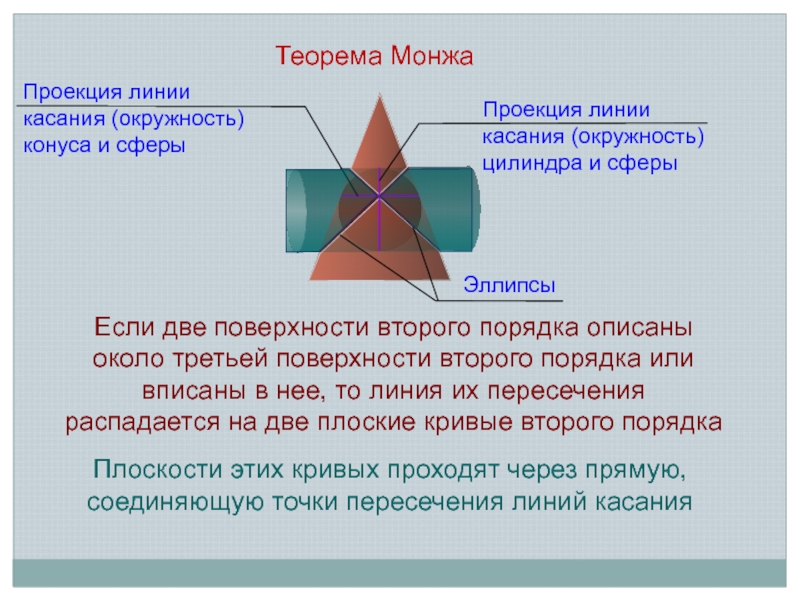
Теорема Монжа
Если две поверхности второго порядка описаны около третьей поверхности второго
Плоскости этих кривых проходят через прямую, соединяющую точки пересечения линий касания
Проекция линии касания (окружность) цилиндра и сферы
Проекция линии касания (окружность) конуса и сферы
Эллипсы