- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Введение.Точка.Прямая.( Лекция № 1) презентация
Содержание
- 1. Введение.Точка.Прямая.( Лекция № 1)
- 2. План лекции
- 3. Инженерная графика (Черчение) Начертательная геометрия. Введение Входят в список дисциплин, составляющих основу инженерного образования.
- 4. Начертательная геометрия- наука о проекционных изображениях. Предметом
- 5. В инженерной графике изучают: методы изображения
- 6. Литература Ляшков А.А., Куликов Л.К., Панчук К.Л.
- 7. Гордон В.О., Семенцов – Огиевский М.А.
- 8. Историческая справка С древних времён человек
- 9. Эпоха Возрождения вызвала расцвет архитектуры, скульптуры, живописи.
- 10. Дополнил линейную перспективу учением "Об уменьшении цветов
- 11. Ввел метод координат французский архитектор Историческая справка Жерар Дезарг (1593 -1662)
- 12. 1795 г. - появилась "Начертательная геометрия" Гаспара
- 13. Первый учебник по начертательной геометрии опубликован
- 14. 1900 г. – в Сибири, в
- 16. П1 А1 В1 С1 A
- 18. П1 А1 В1 С1 A
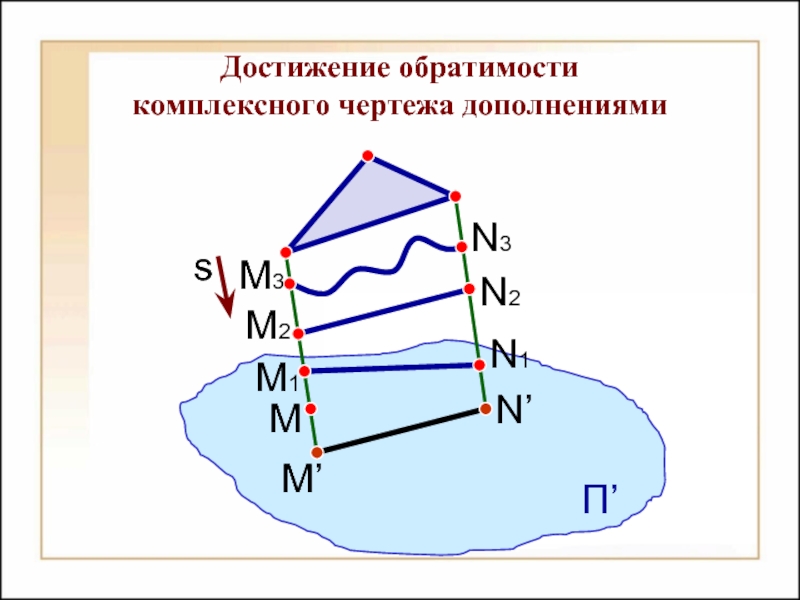
- 19. Достижение обратимости комплексного чертежа
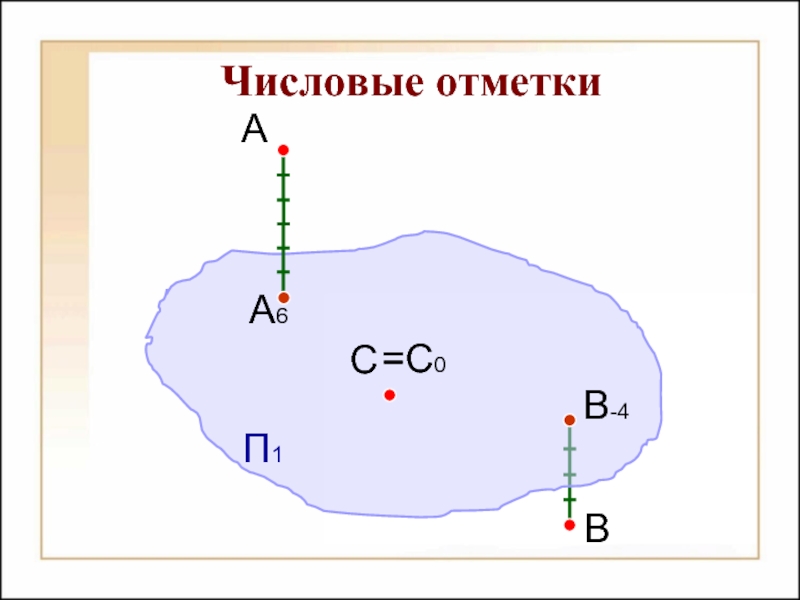
- 20. Числовые отметки А6 A
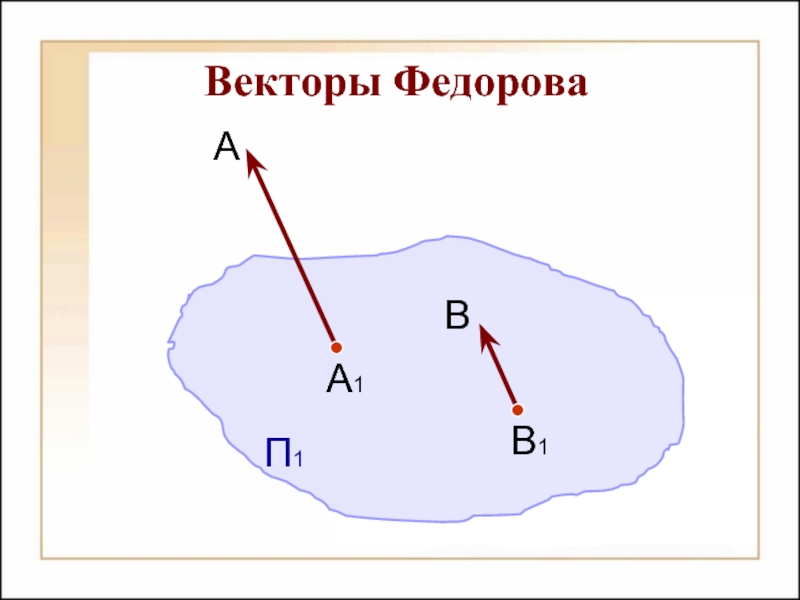
- 21. Векторы Федорова П1 А1 В1 А В
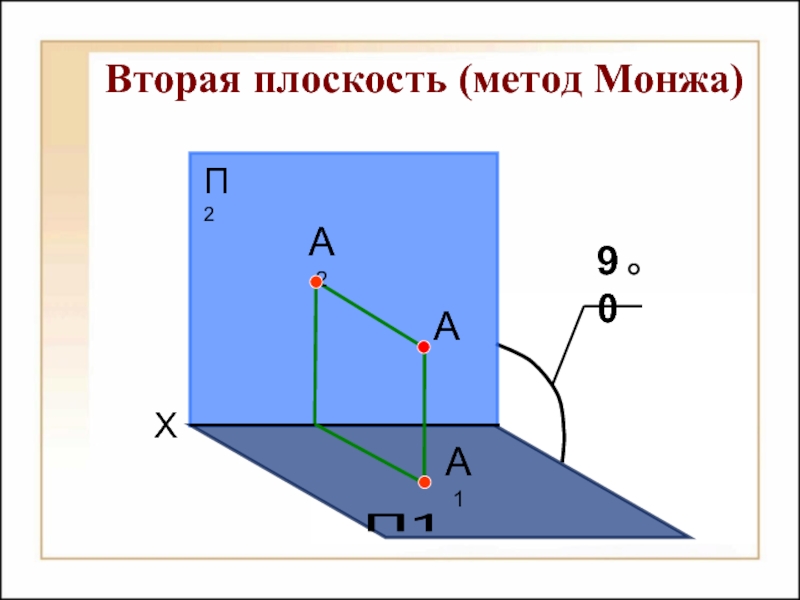
- 22. Вторая плоскость (метод Монжа)
- 23. VIII VII VI -У
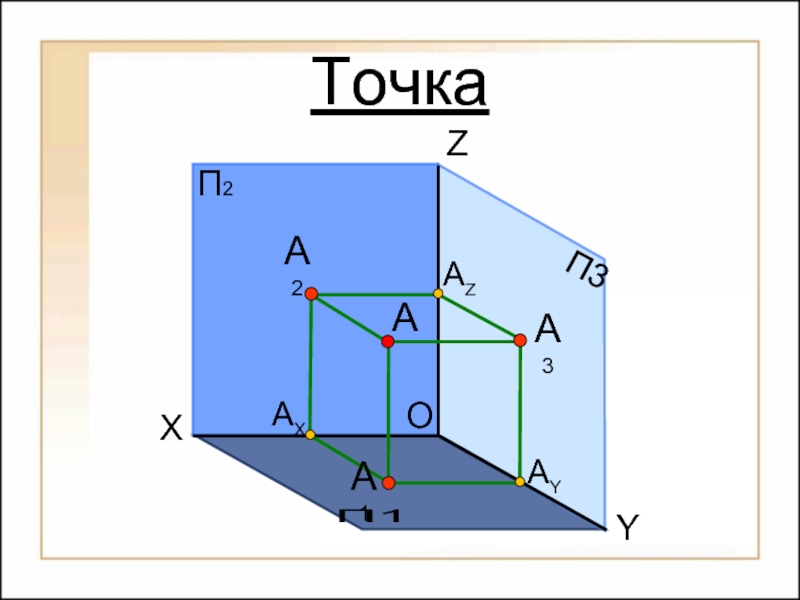
- 24. Точка O П2
- 25. O X Y
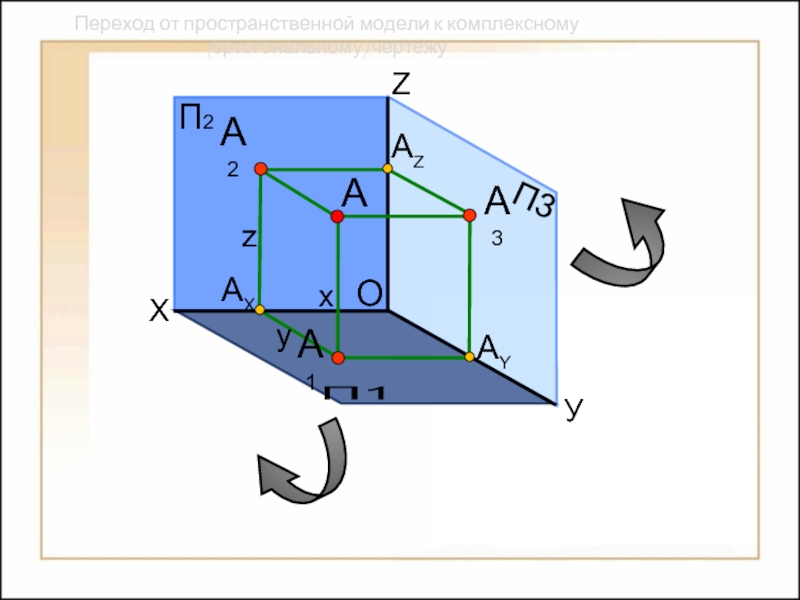
- 26. Переход от пространственной модели к комплексному (ортогональному) чертежу
- 27. П2 П1 П3
- 28. АY А1 А3
- 29. Переход от пространственной модели к
- 30. Переход от пространственной модели к
- 31. Переход от пространственной модели к
- 32. Переход от пространственной модели к
- 33. Переход от пространственной модели к
- 34. 1. Положение точки в пространстве
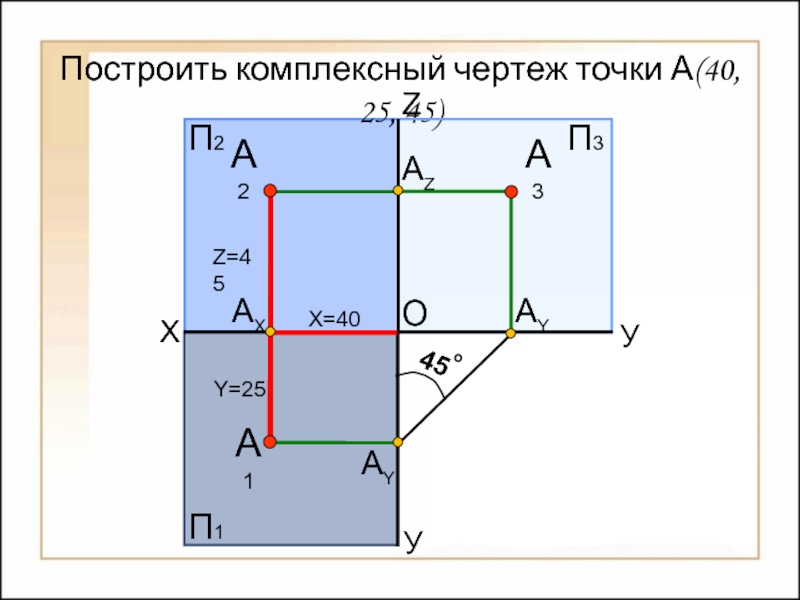
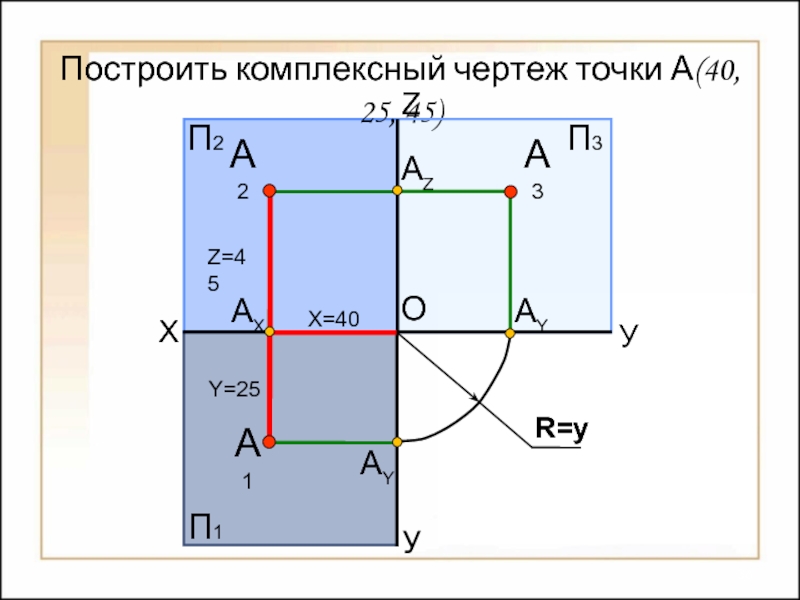
- 35. Построить комплексный чертеж точки А(40,
- 36. Построить комплексный чертеж точки А(40,
- 37. Линия – это множество всех последовательных
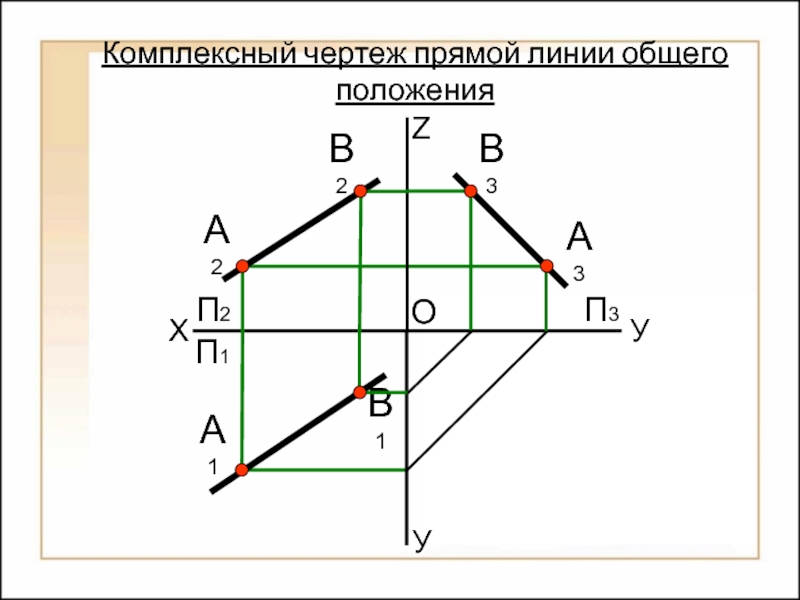
- 38. Прямая линия не параллельная и не
- 39. O П2 П1 X
- 40. X У У А1 O П2
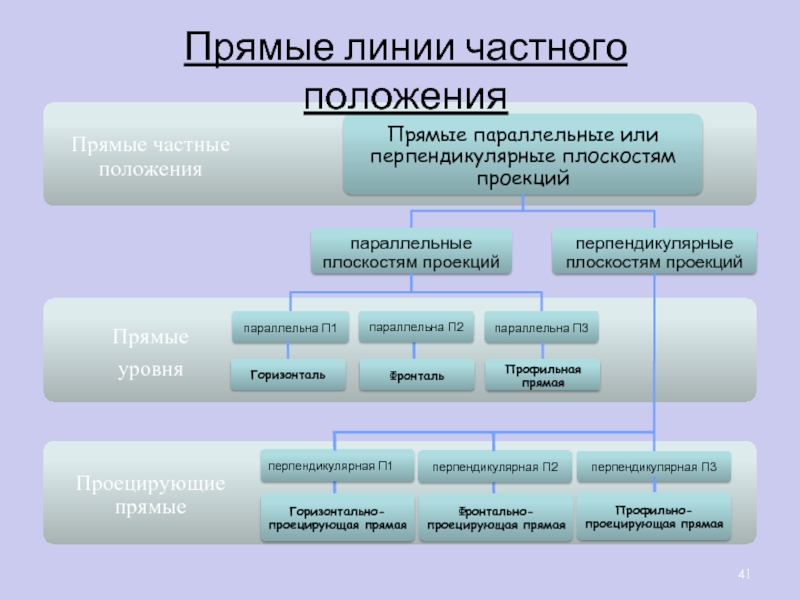
- 41. Прямые линии частного положения
- 42. O П2 П1 X
- 43. X У А1 O П2 Z
- 44. O П2 П1 X
- 45. X У C1 O П2 Z
- 46. Свойства проекций прямых уровня Если прямая
- 47. O П2 П1 X
- 48. O П2 П1 X
- 49. Свойства проекций проецирующих прямых Если прямая
- 50. доценты кафедры «Начертательная геометрия, инженерная и компьютерная
Слайд 3Инженерная графика
(Черчение)
Начертательная геометрия.
Введение
Входят в список дисциплин, составляющих основу инженерного образования.
Слайд 4Начертательная геометрия-
наука о проекционных изображениях.
Предметом начертательной геометрии являются:
Способы построения
Исследование геометрических свойств объектов по их изображениям.
Слайд 5В инженерной графике
изучают:
методы изображения предметов;
правила выполнения и чтения чертежей деталей
Слайд 6Литература
Ляшков А.А., Куликов Л.К.,
Панчук К.Л.
НАЧЕРТАТЕЛЬНАЯ ГЕОМЕТРИЯ
(конспект лекций)
Омск: Изд-во ОмГТУ,
Слайд 7Гордон В.О., Семенцов – Огиевский М.А.
Курс начертательной геометрии: учебник.
Бубенников А.В.
Начертательная геометрия: учебник. –
М.: Высш. шк., 1985.
Фролов С.А.
Начертательная геометрия: учебник. –
М.: ИНФРА–М, 2007.
Слайд 8
Историческая справка
С древних времён человек старался сохранить образ увиденного. Наскальная живопись,
Цивилизация развивалась, появились схемы и карты местности, изображение храмовых комплексов, жилых домов, военных сооружений, мостов, простых механизмов. Потребовалась выработка и первых общих правил представления пространственной информации на плоскости. Семь чудес света трудно представить без первых чертежей, рисунков и схем.
Египетские, греческие и римские учёные, изучая перспективу, пытались выработать некие правила представления имеющейся информации.
Слайд 9Эпоха Возрождения вызвала расцвет архитектуры, скульптуры, живописи. Первые теоретические основы перспективы
Историческая справка
Леон Баттиста
Альберти
(1404 -1472)
Слайд 10Дополнил линейную перспективу учением "Об уменьшении цветов и отчётливости очертаний".
Историческая
Леонардо да
Винчи
(1452 -1519)
Слайд 121795 г. - появилась "Начертательная геометрия" Гаспара Монжа, им введено понятие
Историческая справка
Гаспар
Монж
(1746 -1818)
Основоположник начертательной геометрии -
Слайд 13
Первый учебник по начертательной геометрии опубликован во Франции в 1798 г.
Россия.
1810 г. – Карл Потье читает в С.-Петербурге первые лекции в Институте корпуса инженеров путей сообщения.
1821 г. – Я.А. Севастьянов (1796-1849) издает оригинальный курс начертательной геометрии на русском языке.
Историческая справка
Слайд 14
1900 г. – в Сибири, в Томском техническом институте курс начертательной
Историческая справка
Позже в России начертательная геометрия развивалась трудами Н. Макарова, В. Курдюмова, А. Власова, Н. Глаголева, Н. Четверухина и многих других.
Валентином
Николаевичем
Джонсом
28(16)октября 1900г.
Слайд 18
П1
А1
В1
С1
A
C
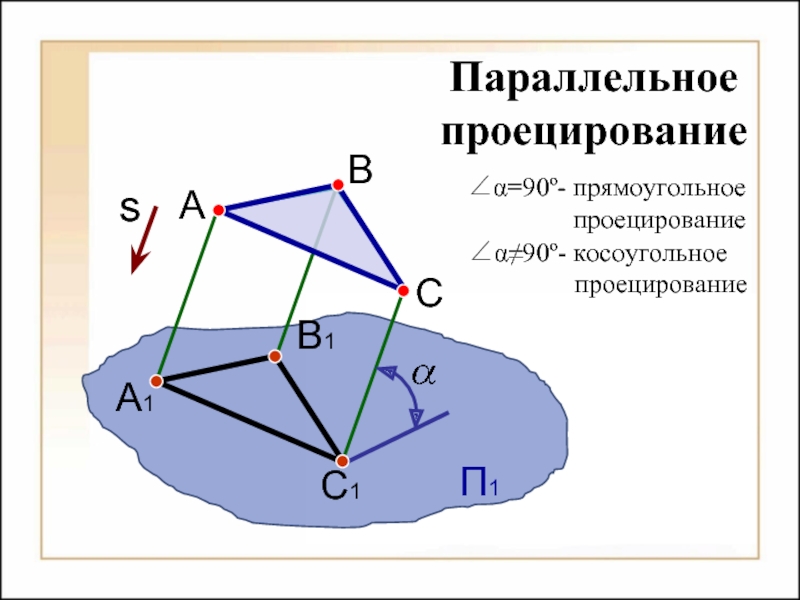
Параллельное
проецирование
B
∠α=90º- прямоугольное
проецирование
∠α≠90º- косоугольное
s
Слайд 23
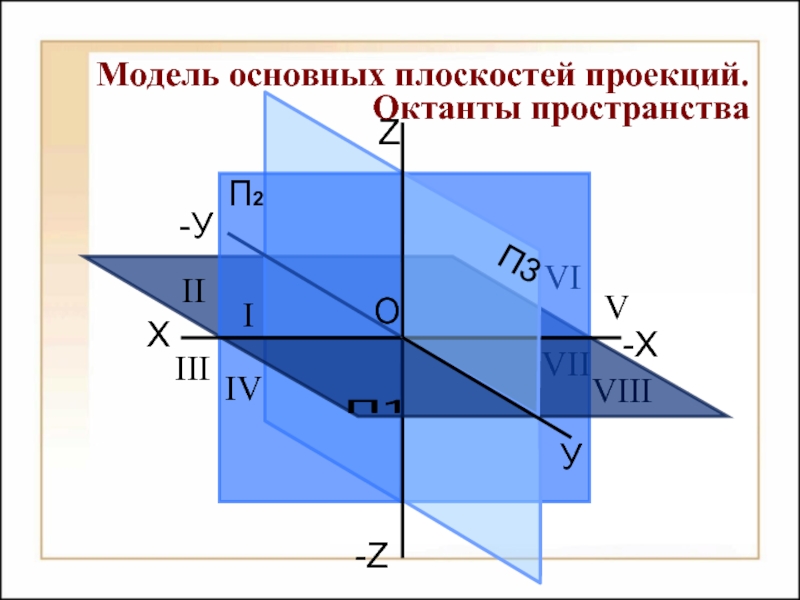
VIII
VII
VI
-У
X
П1
П2
П3
-X
У
Z
-Z
I
II
O
IV
V
III
Модель основных плоскостей проекций. Октанты пространства
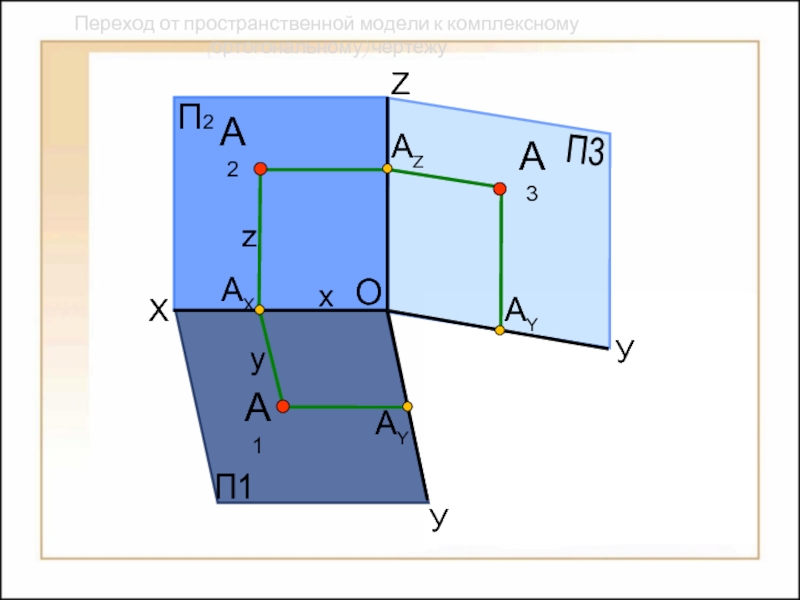
Слайд 27
П2
П1
П3
X
Z
АX
АY
А1
А
А2
А3
АZ
Переход от пространственной модели к комплексному (ортогональному) чертежу
O
x
y
z
У
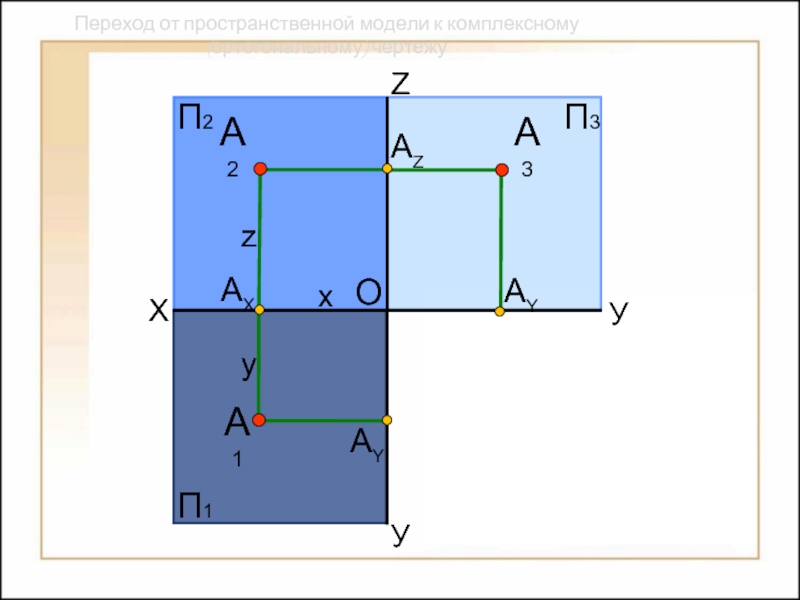
Слайд 28
АY
А1
А3
Переход от пространственной модели к комплексному (ортогональному) чертежу
АY
П1
П3
X
У
У
АZ
П2
Z
А2
АX
O
x
y
z
Слайд 29
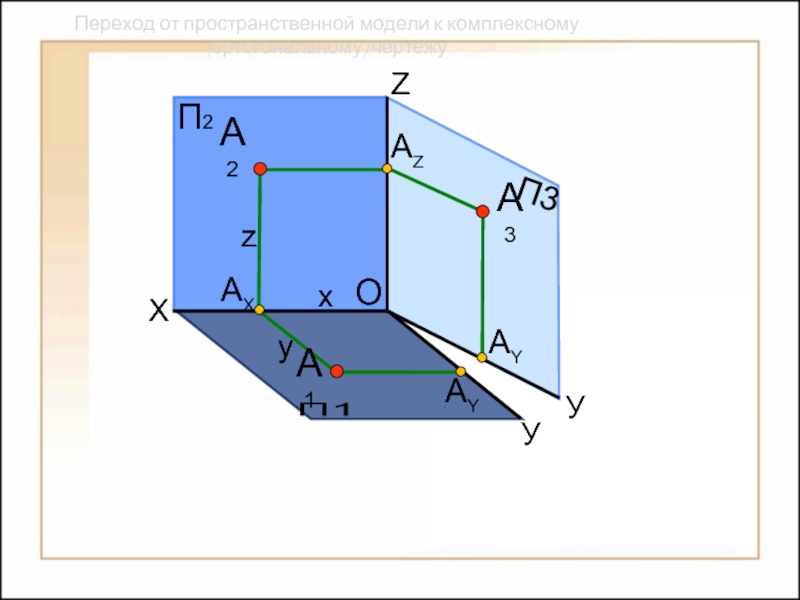
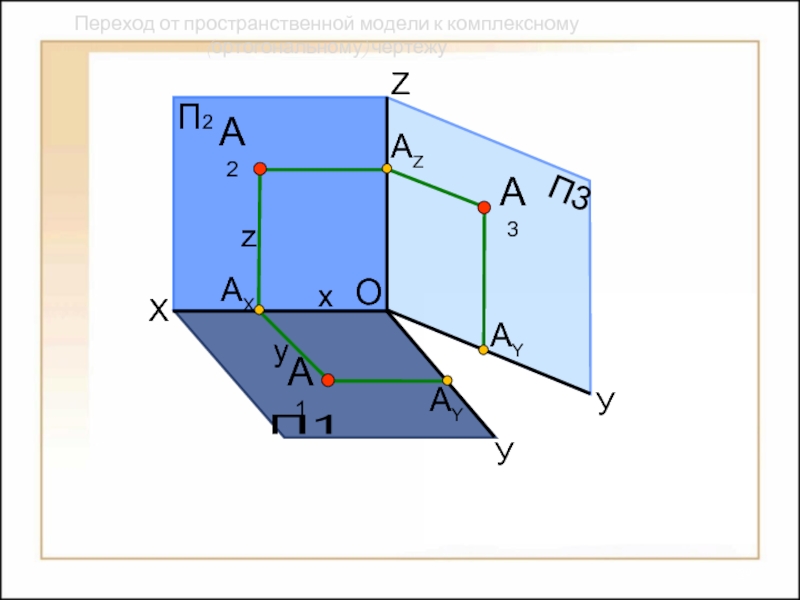
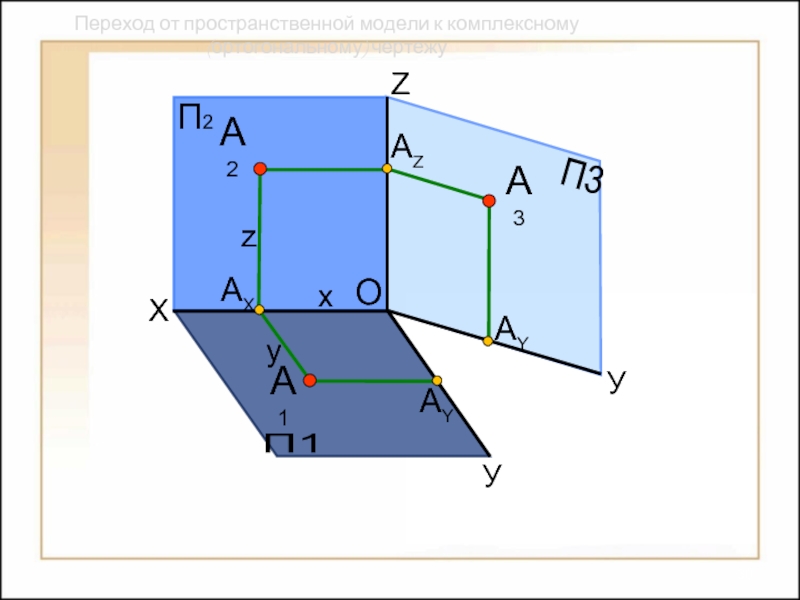
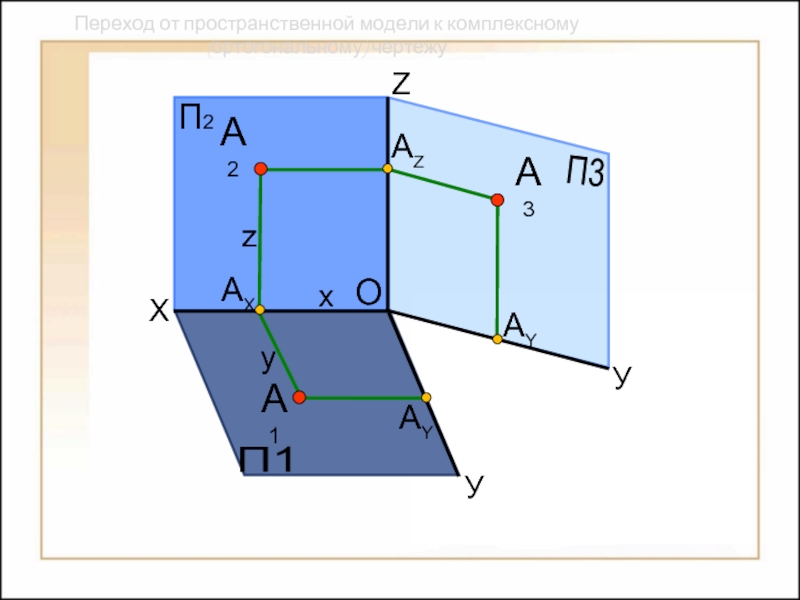
Переход от пространственной модели к комплексному (ортогональному) чертежу
П1
П3
X
У
У
O
АY
А1
А3
АY
АX
АZ
П2
Z
А2
x
y
z
Слайд 30
Переход от пространственной модели к комплексному (ортогональному) чертежу
П1
П3
X
У
У
АY
А1
А3
АY
АX
АZ
П2
Z
А2
x
y
z
O
Слайд 31
Переход от пространственной модели к комплексному (ортогональному) чертежу
X
У
У
П1
П3
АY
А1
А3
АY
АX
АZ
П2
Z
А2
x
y
z
O
Слайд 32
Переход от пространственной модели к комплексному (ортогональному) чертежу
X
У
У
П1
П3
АY
А1
А3
АY
АX
АZ
П2
Z
А2
x
y
z
O
Слайд 33
Переход от пространственной модели к комплексному (ортогональному) чертежу
X
У
У
АY
А1
АY
АX
АZ
П2
Z
А2
П1
П3
А3
x
y
z
O
Слайд 34
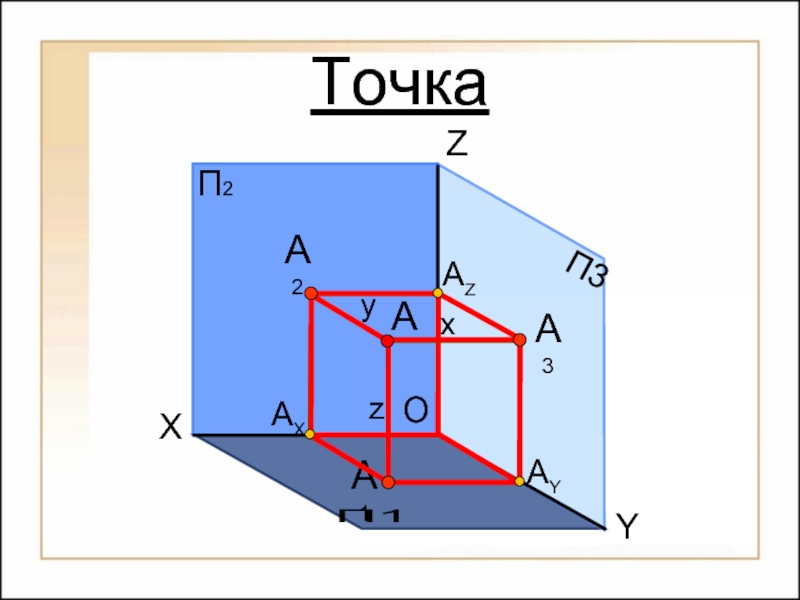
1. Положение точки в пространстве определяется тремя координатами
A(x, y,
2. Положение проекции точки на плоскости проекций определяется двумя координатами
А1(x, y), А2(x, z), А3(y, z);
3. Две проекции точки определяют ее положение в пространстве;
4. Две проекции точки лежат на линии связи, перпендикулярной координатной оси.
Слайд 37
Линия – это множество всех последовательных положений двигающейся точки.
Прямая линия –
точки не меняющей своего
направления.
Прямая линия
Прямая линия
может быть задана:
1. Двумя точками ей принадлежащими
2. Одной точкой и направлением линии
Слайд 38
Прямая линия не параллельная и не перпендикулярная ни одной из плоскостей
Прямая линия общего положения
Замечание:
На комплексном чертеже проекции прямой общего положения не параллельны и не перпендикулярны ни одной координатной оси.
Слайд 43
X
У
А1
O
П2
Z
А2
П1
П3
А3
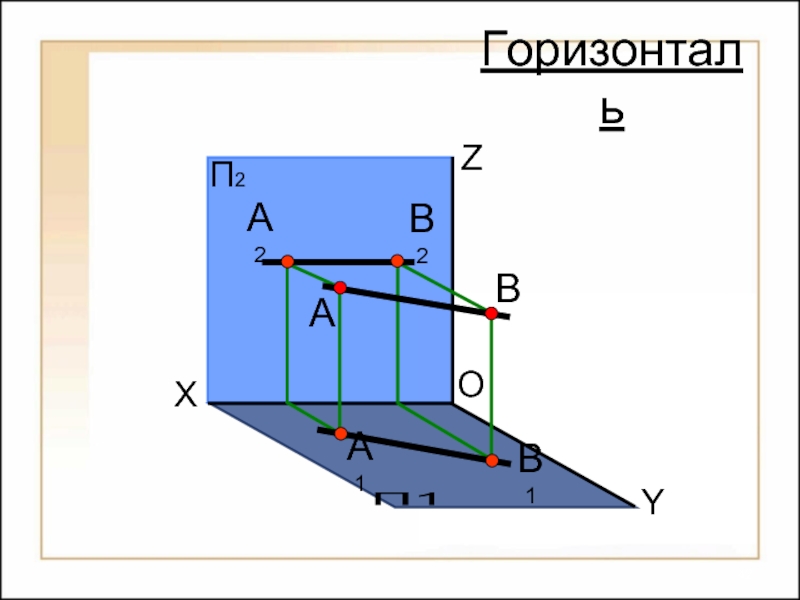
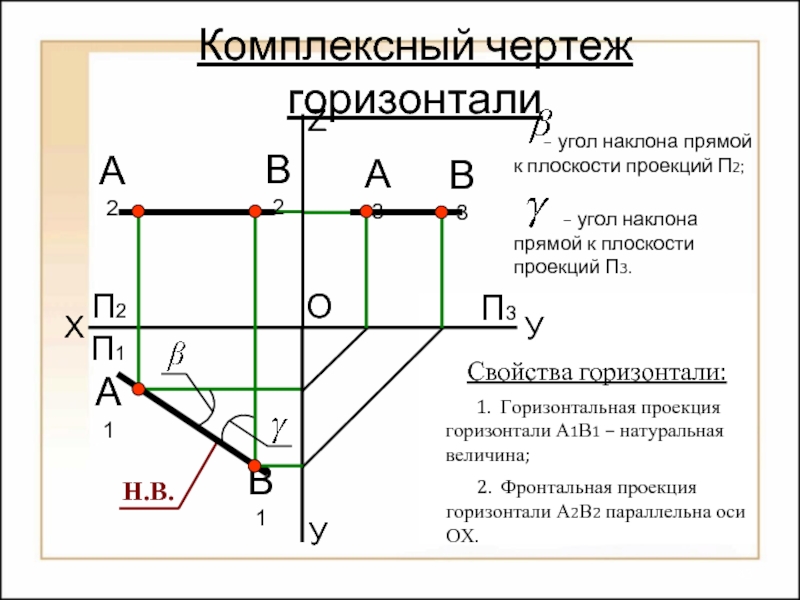
Комплексный чертеж горизонтали
В1
В2
В3
Н.В.
Свойства горизонтали:
1. Горизонтальная проекция горизонтали
У
2. Фронтальная проекция горизонтали А2В2 параллельна оси ОХ.
Слайд 45
X
У
C1
O
П2
Z
С2
П1
П3
C3
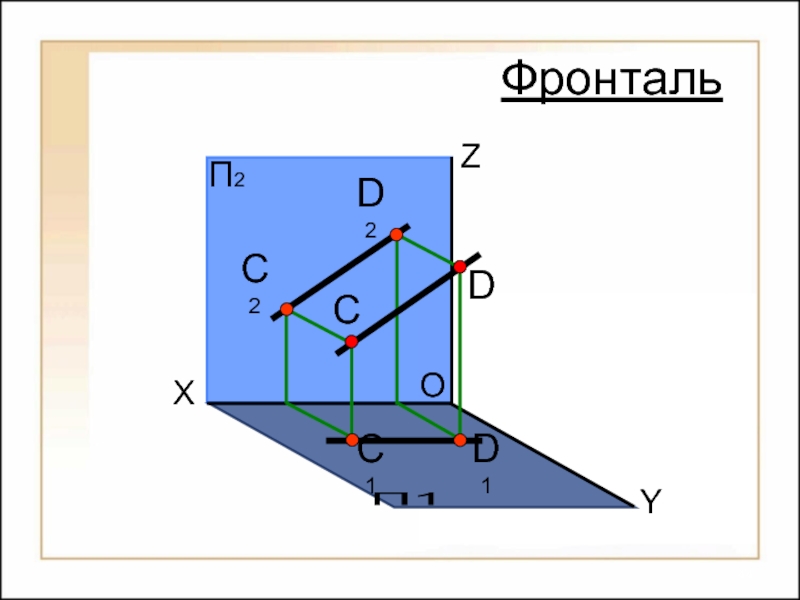
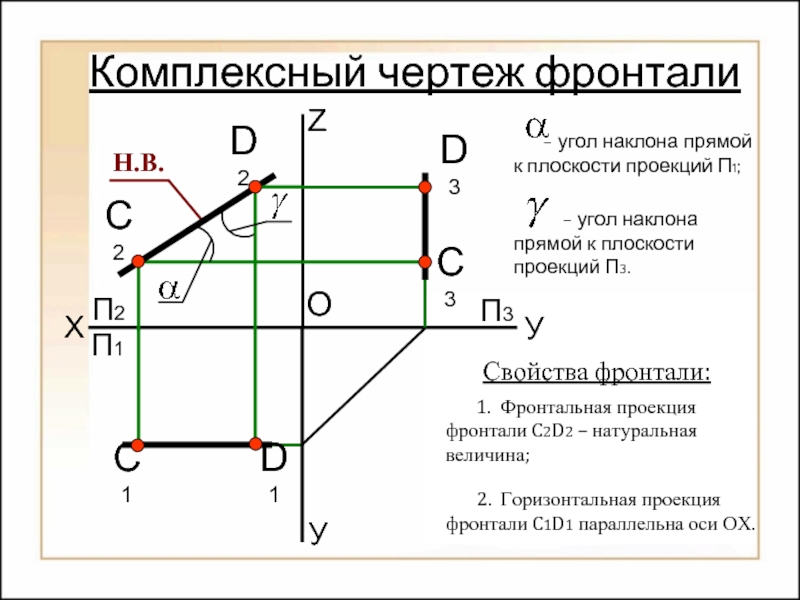
Комплексный чертеж фронтали
D1
D2
D3
Н.В.
Свойства фронтали:
1. Фронтальная проекция фронтали
У
2. Горизонтальная проекция фронтали C1D1 параллельна оси ОХ.
Слайд 46
Свойства проекций прямых уровня
Если прямая параллельна плоскости проекций, то:
на
проекции прямой на две другие плоскости проекций, параллельны координатным осям.
Слайд 47
O
П2
П1
X
Y
Z
А
А2
А1=В1
В
В2
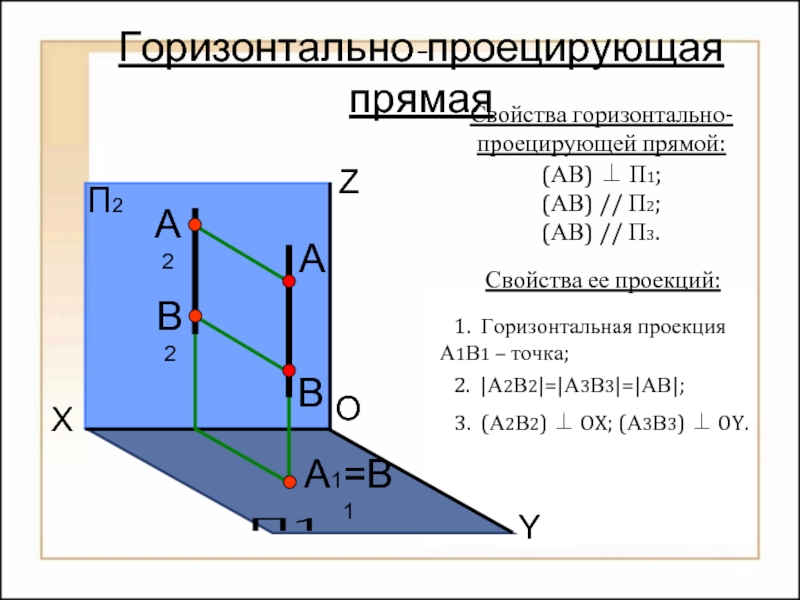
Горизонтально-проецирующая прямая
Свойства горизонтально-проецирующей прямой:
(АВ) ⊥ П1;
(АВ) // П2;
(АВ) // П3.
Свойства
1. Горизонтальная проекция А1В1 – точка;
2. |А2В2|=|А3В3|=|АВ|;
3. (А2В2) ⊥ OX; (А3В3) ⊥ OY.
Слайд 48
O
П2
П1
X
Y
Z
С
С1
D
С2=D2
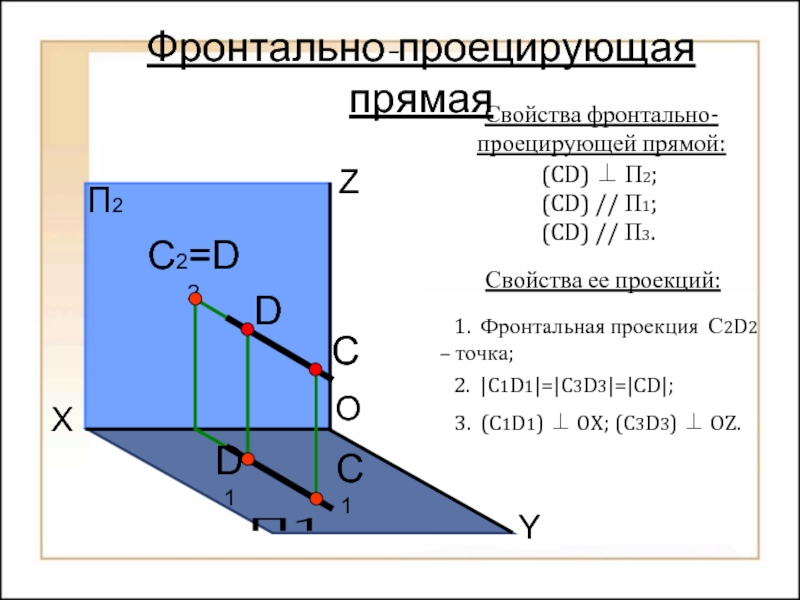
Фронтально-проецирующая прямая
Свойства фронтально-проецирующей прямой:
(CD) ⊥ П2;
(CD) // П1;
(CD) // П3.
Свойства
1. Фронтальная проекция С2D2 – точка;
2. |C1D1|=|C3D3|=|CD|;
3. (C1D1) ⊥ OX; (C3D3) ⊥ OZ.
D1
Слайд 49
Свойства проекций проецирующих прямых
Если прямая перпендикулярна плоскости проекций, то:
на
проекции прямой на две другие плоскости проекций проецируются в натуральную величину и перпендикулярны координатным осям.
Слайд 50доценты кафедры «Начертательная геометрия, инженерная и компьютерная графика» Омского Государственного технического
Авторы:
Бондарев
Олег Александрович, к.т.н.,
Кайгородцева
Наталья Викторовна, к.пед.н.