технический университет имени Н.Э.Баумана
2015г.
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Способы преобразования чертежа презентация
Содержание
- 1. Способы преобразования чертежа
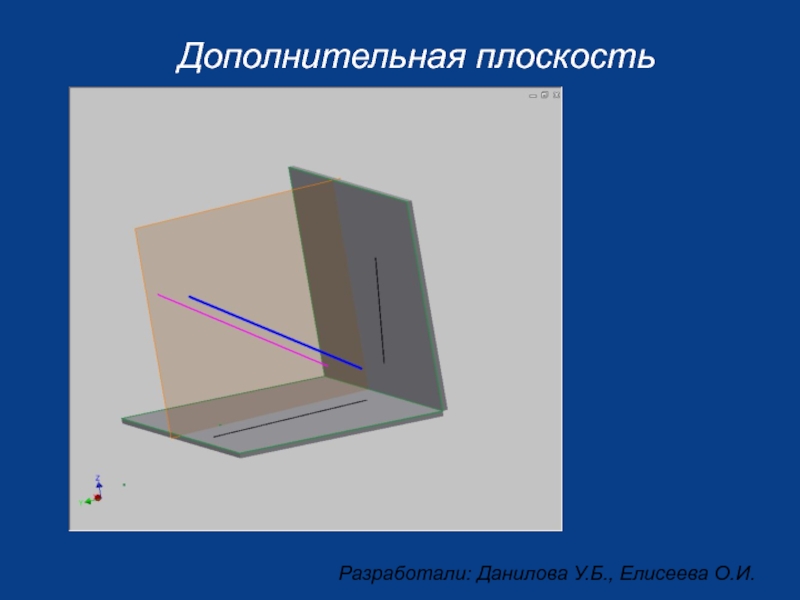
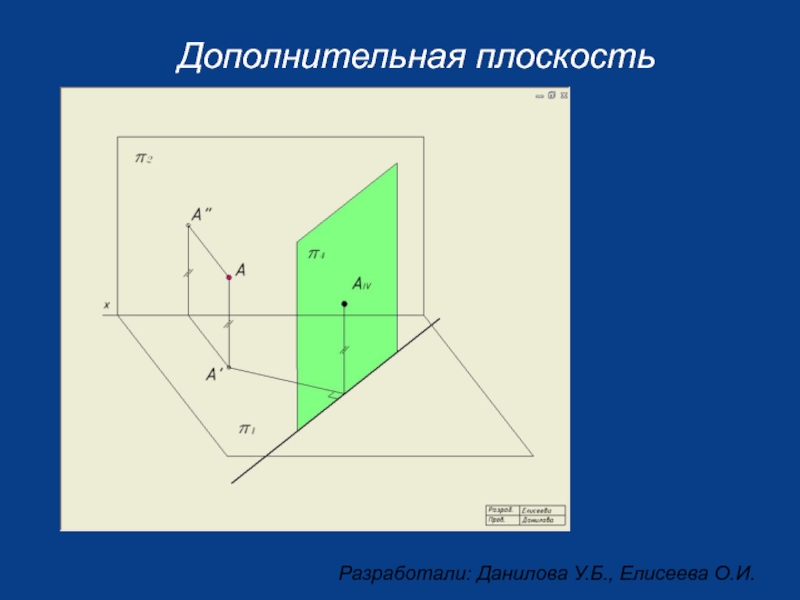
- 2. Дополнительная плоскость
- 3. Дополнительная плоскость
- 4. 1. Задаем новую плоскость p4 параллельно одной
- 5. Задача 54. Построить натуральный вид сечения призмы
- 6. Задаем новую плоскость p4 перпендикулярно проекции горизонтали
- 7. 1.Задаем новую плоскость p4: p4 bA’ B’
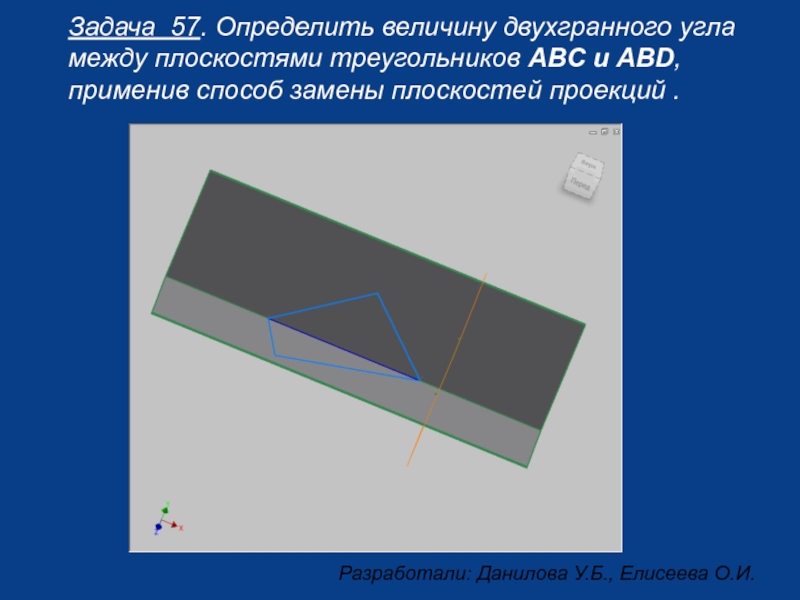
- 8. Задача 57. Определить величину двухгранного угла между
- 9. Задача 58. Повернуть отрезок АВ вокруг
- 10. Задача 58. Повернуть отрезок АВ вокруг
- 11. Задача 61. Определить угол наклона плоскости a
Дополнительная плоскость
Слайд 1Начертательная геометрия Семинар №7 Способы преобразования чертежа. Подготовили: Данилова У.Б., Елисеева О.И. Московский государственный
Слайд 41. Задаем новую плоскость p4 параллельно одной из проекций отрезка.
2 .
Задаем еще одну плоскость p5 перпендикулярно проекции отрезка.
Задача 51. Заменой плоскостей проекций преобразовать чертеж отрезка АВ так, чтобы в новой системе плоскостей проекций отрезок занял проецирующее положение.
AVI
x1
BVI
=BV
AV
p1
p2
p4
p4
p5
p1
x2
IAВI
zВ
zВ
zA
zA
Слайд 5Задача 54. Построить натуральный вид сечения призмы плоскостью a ,
используя способ замены плоскостей проекций.
x1
1 I
p2
p2
p4
p1
y1
6 I
5 I
4 I
3 I
2 I
=y4
y6
y2
=y3
=y5
1 II
2 II
=6 II
3 II
=5 II
4 II
1 IV
3 IV
4 IV
5 IV
2 IV
6 IV
Cечение на чертеже.
Слайд 6Задаем новую плоскость p4 перпендикулярно проекции горизонтали CD.
= IAKI
Задача 55. Определить расстояние от точки А до плоскости D ВСD , применив способ замены плоскостей проекций. Построить проекции отрезка, определяющего это расстояние.
AVI
x1
BVI
p1
p2
p4
p1
zВ
zA
СVI
=DVI
KVI
IAKI
K I
K II
AVIKVI
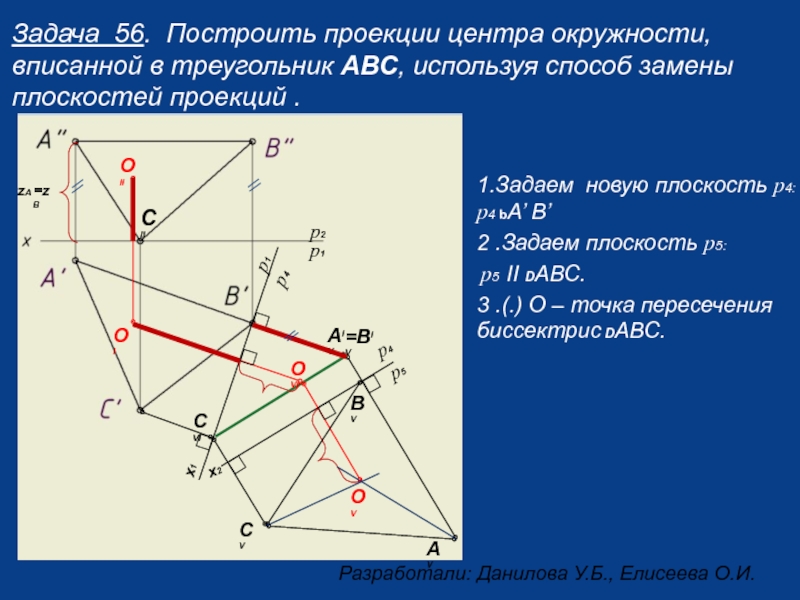
Слайд 71.Задаем новую плоскость p4: p4 bA’ B’
2 .Задаем плоскость p5:
p5 II DАВС.
3 .(.) О – точка пересечения биссектрис DАВС.
3 .(.) О – точка пересечения биссектрис DАВС.
Задача 56. Построить проекции центра окружности, вписанной в треугольник АВС, используя способ замены плоскостей проекций .
AV
x1
С VI
=ВIV
AIV
p1
p2
p4
p4
p5
p1
x2
=zВ
zA
С V
OV
OVI
O I
O II
ВV
С II
Слайд 8Задача 57. Определить величину двухгранного угла между плоскостями треугольников АВС и
АВD, применив способ замены плоскостей проекций .
Слайд 9Задача 58. Повернуть отрезок АВ вокруг прямой i так, чтобы
он стал параллелен фронтальной плоскости проекций.
_
А’’
f0a
Решение.
a-Плоскость вращения точки А.
IА’В’I – радиус вращения точки А.
3. O – центр вращения точки А
Граничное условие: отрезок АВ должен стать параллельным плоскости p2 , т.е. горизонтальная проекция отрезка АВ должна быть параллельной оси Х.
_
А’
Rвр
Гр.усл.
IАВI
O’
O’’
Слайд 10Задача 58. Повернуть отрезок АВ вокруг прямой i так, чтобы
он стал параллелен фронтальной плоскости проекций.
Решение.
a-Плоскость вращения точки А.
IА’В’I – радиус вращения точки А.
3. O – центр вращения точки А
Граничное условие: отрезок АВ должен стать параллельным плоскости p2 , т.е. горизонтальная проекция отрезка АВ должна быть параллельной оси Х.
IАВI
~
~
f0a
O’’
O’
Гр.усл.
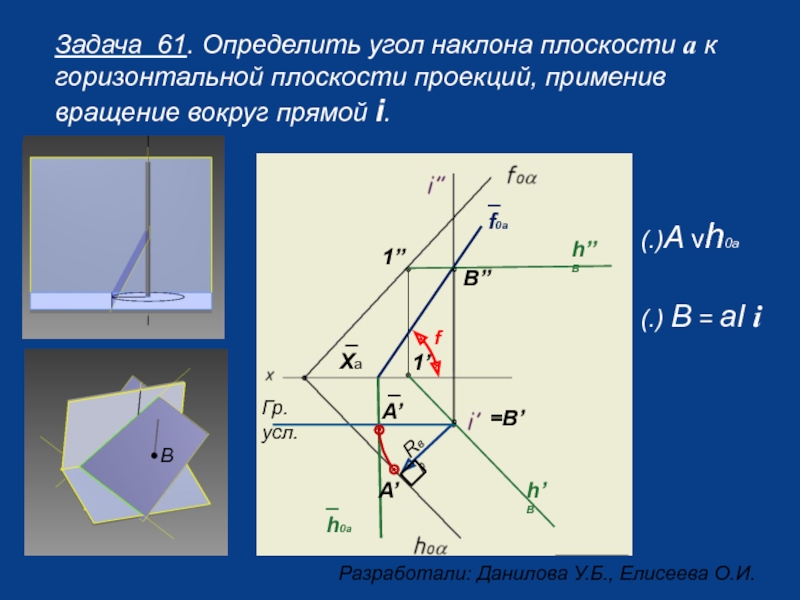
Слайд 11Задача 61. Определить угол наклона плоскости a к горизонтальной плоскости проекций,
применив вращение вокруг прямой i.
_
Xa
_ f0a
(.)А vh0a
(.) В = aI i
_
А’
Rвр
Гр.усл.
А’
=В’
В’’
h’’В
h’В
1’’
1’
_ h0a
f
В
