Способы преобразования чертежа презентация

Содержание

Преобразование комплексного чертежа (ЭПЮРА) Основным принципом является ПРЕОБРАЗОВАНИЕ проекций геометрических объектов в новые, удобные для решения задачи условия

Слайд 1Способы преобразования чертежа
Принципы преобразования эпюра
Основные задачи преобразования
Три способа преобразования
Лекция 8
Лектор Стриганова

Л.Ю.

Слайд 2Преобразование комплексного чертежа (ЭПЮРА)
Основным принципом является ПРЕОБРАЗОВАНИЕ
проекций геометрических объектов

в новые, удобные для решения задачи условия

Слайд 3Три основные способа преобразования
Способ перемены (замены) плоскостей проекций
Способ плоскопараллельного перемещения
Способ вращения

вокруг проецирующих прямых

Слайд 4Применение способов преобразования
Решение метрических задач (определение натуральной величины заданных объектов)

Решение позиционных

и конструктивных задач (нахождение линий пересечения поверхностей)

Слайд 5 Позиционные задачи
нахождение относительного положения геометрических объектов


Слайд 6Круг позиционных задач
∙ относительное положение точек

∙ относительное положение прямых линий
∙ относительное положение прямой и
плоскости
∙ относительное положение плоскостей
∙ относительное положение плоскости
и поверхности
∙ относительное положение поверхностей

Слайд 7 Метрические - задачи на определение расстояний и натуральных величин геометрических

объектов

Слайд 8 Конструктивные – задачи на построение геометрических фигур, отвечающих заданным

условиям

Слайд 9ЧЕТЫРЕ ОСНОВНЫЕ ЗАДАЧИ, РЕШАЕМЫЕ СПОСОБАМИ ПРЕОБРАЗОВАНИЯ
ПРЕОБРАЗОВАТЬ ПРЯМУЮ ОБЩЕГО ПОЛОЖЕНИЯ В ПРЯМУЮ

ЧАСТНОГО ПОЛОЖЕНИЯ (ГОРИЗОНТАЛЬ ИЛИ ФРОНТАЛЬ)

ПРЕОБРАЗОВАТЬ ПРЯМУЮ ЧАСТНОГО ПОЛОЖЕНИЯ В ПРЯМУЮ ПРОЕЦИРУЮЩУЮ

ПРЕОБРАЗОВАТЬ ПЛОСКОСТЬ ОБЩЕГО ПОЛОЖЕНИЯ В ПЛОСКОСТЬ ПРОЕЦИРУЮЩУЮ

4. ПРЕОБРАЗОВАТЬ ПЛОСКОСТЬ ПРОЕЦИРУЮЩУЮ В ПЛОСКОСТЬ УРОВНЯ

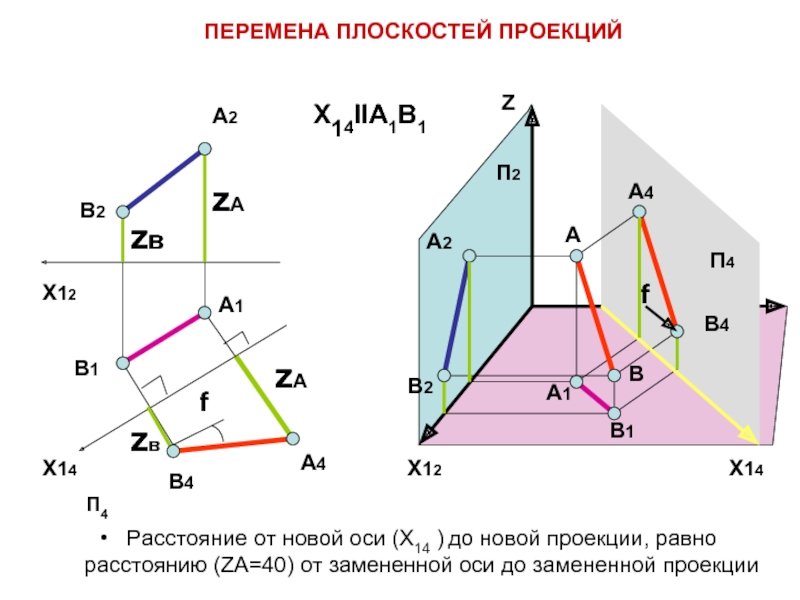
Слайд 10Сущность способа перемены плоскостей проекций
ЗАДАННЫЙ ГЕОМЕТРИЧЕСКИЙ ОБЪЕКТ НЕПОДВИЖЕН

ВВОДЯТСЯ НОВЫЕ ПЛОСКОСТИ

ПРОЕКЦИЙ ПАРАЛЛЕЛЬНЫЕ ИЛИ ПЕРПЕНДИКУЛЯРНЫЕ ЗАДАННОМУ ГЕОМЕТРИЧЕСКОМУ ОБЪЕКТУ

Слайд 11



Расстояние от новой оси до новой проекции, равно расстоянию от замененной

оси до замененной проекции

Y

X12

Z

А

В

А1

В1

А2

В2

В4

А4









X14

П4

П1

П2



ПЕРЕМЕНА ПЛОСКОСТЕЙ ПРОЕКЦИЙ

П4 ┴ П1
П4 II АВ


X14IIA1B1

Слайд 12Позиционная задача
Определить углы

наклона прямой к горизонтальной и фронтальной плоскостям проекций, если А(15,40,10); В(65,30,15).
Задачу решить способом перемены плоскостей проекций

(f и y)

Слайд 13
ПЕРЕМЕНА ПЛОСКОСТЕЙ ПРОЕКЦИЙ


А1
В1
А2
В2
В4
А4




X12
Z
А
В
А1
В1
А2
В2
В4
А4








X14
П4
П2




X12
X14
Расстояние от новой оси (X14 ) до новой проекции,

равно расстоянию (ZA=40) от замененной оси до замененной проекции

f

zв

zв

zА

zА


f

X14IIA1B1

П4

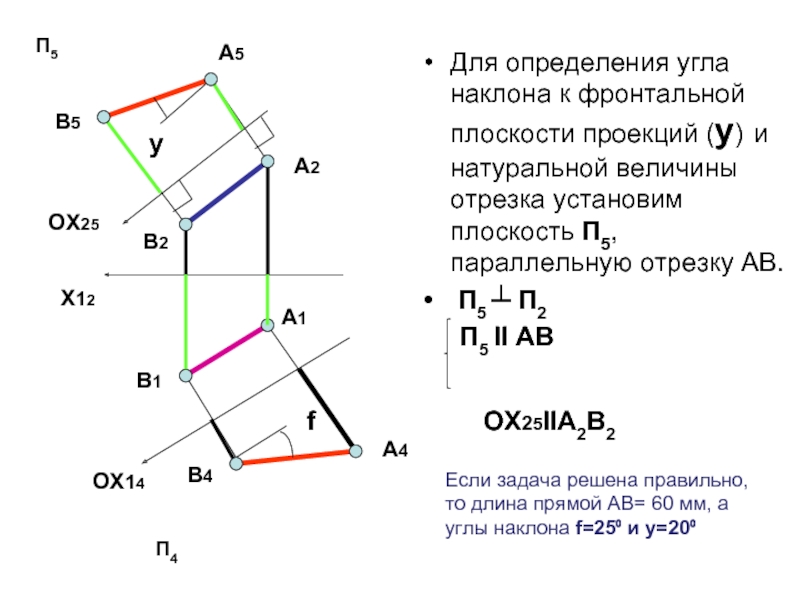
Слайд 14Для определения угла наклона к фронтальной плоскости проекций (y) и натуральной

величины отрезка установим плоскость П5, параллельную отрезку АВ.
П5 ┴ П2
П5 II АВ




А1

В1

А2

В2

В4

А4



X12

ОX14


f

А5



ОX25

В5

y




ОX25IIA2B2

П5

П4

Если задача решена правильно, то длина прямой АВ= 60 мм, а углы наклона f=25⁰ и y=20⁰


Слайд 15Метрическая задача
Определить натуральную величину треугольника АВС и угол его наклона к

горизонтальной плоскости проекций
А(90,20,0); В(60,50,40); С(20,20,10)

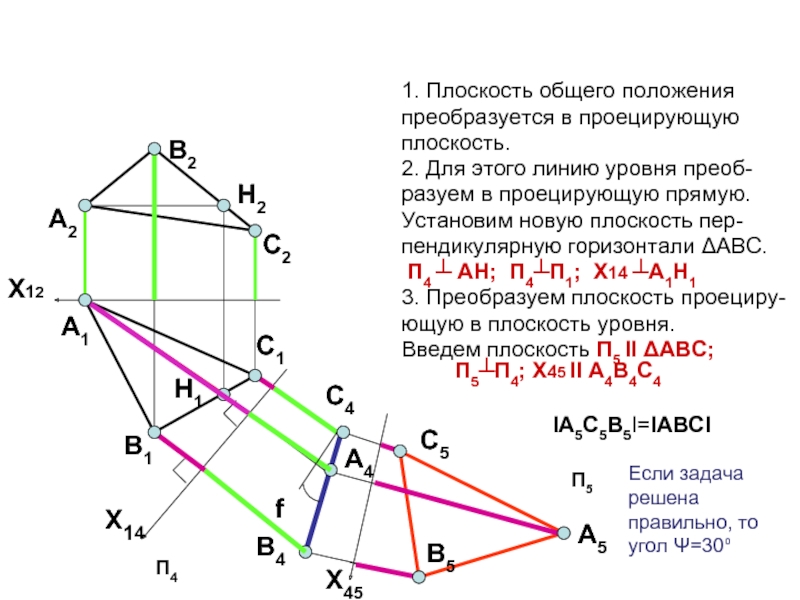
Слайд 161. Плоскость общего положения
преобразуется в проецирующую
плоскость.
2. Для этого линию

уровня преоб-
разуем в проецирующую прямую.
Установим новую плоскость пер-
пендикулярную горизонтали ΔАВС.
П4 ┴ АH; П4┴П1; X14 ┴A1H1
3. Преобразуем плоскость проециру-
ющую в плоскость уровня.
Введем плоскость П5 ІІ ΔАВС; П5┴П4; X45 II A4B4C4


X12

A1

B2

B1

C1

C2

A2

H2

H1

X14









A4

B4

C4

X45

В5

С5

А5







ІА5С5В5І=ІАВСІ


f

П4

П5


Если задача решена правильно, то угол Ψ=30⁰

Слайд 17Сущность способа плоскопараллельного перемещения
Заданный геометрический объект совершает плоскопараллельное движение, при котором

ВСЕ ЕГО ТОЧКИ движутся параллельно некоторой плоскости до положения параллельного или перпендикулярного плоскости проекций

Линия по которой происходит перемещение всех точек объекта находится В ПЛОСКОСТИ УРОВНЯ

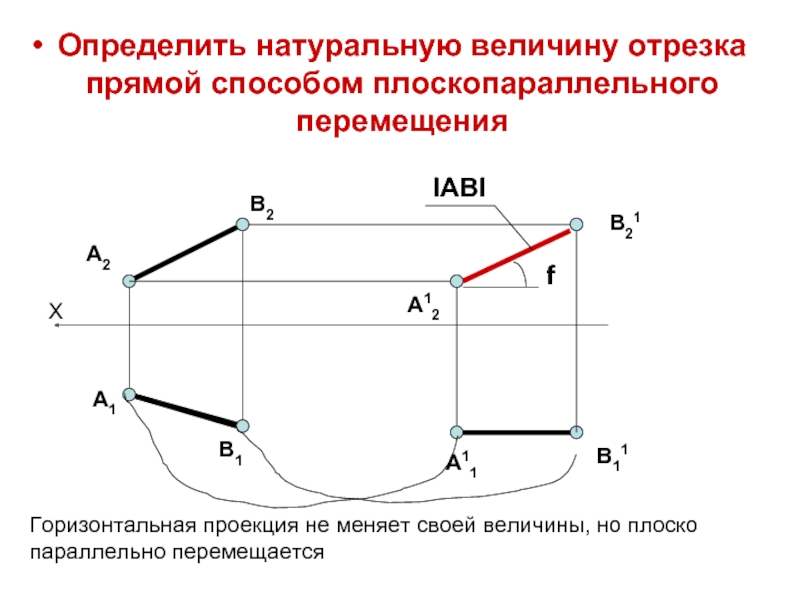
Слайд 18Определить натуральную величину отрезка прямой способом плоскопараллельного перемещения





X
A2
B1
A1
B2
A11
B11


A12
B21


f
IАВI
Горизонтальная проекция не меняет

своей величины, но плоско параллельно перемещается



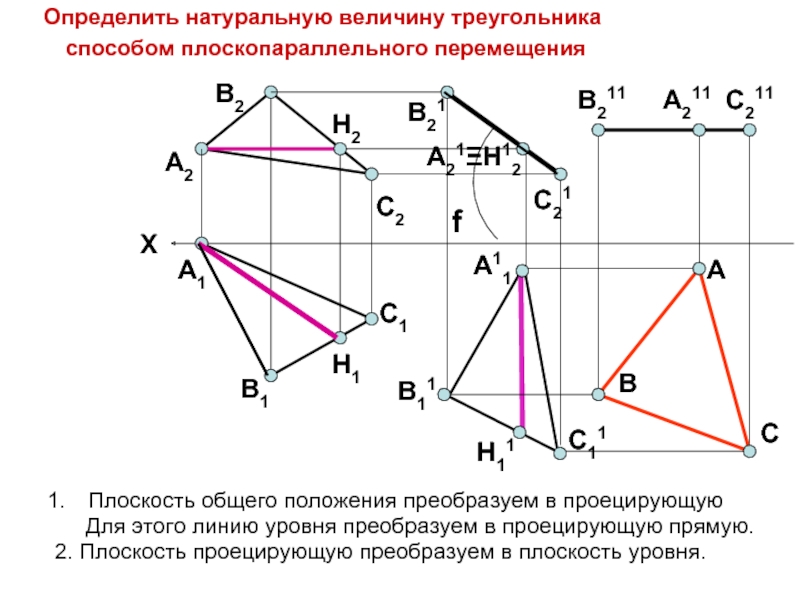
Слайд 19Плоскость общего положения преобразуем в проецирующую
Для

этого линию уровня преобразуем в проецирующую прямую.
2. Плоскость проецирующую преобразуем в плоскость уровня.

Определить натуральную величину треугольника
способом плоскопараллельного перемещения

X

A1

B1

C1

C2



B2

A2



A11

C11


B11




C21

B21

A21ΞH12



B211

A211

C211

B

A

C











H1

H2

H11



f

Слайд 20Сущность способа вращения вокруг прямых перпендикулярных плоскостям проекций
Заданный геометрический объект вращается

вокруг оси до положения параллельного или перпендикулярного какой-либо плоскости проекций.

Все точки объекта движутся по окружностям, которые располагаются в плоскостях уровня, перпендикулярных оси вращения.

Слайд 21Определить натуральную величину отрезка прямой способом вращения вокруг прямых перпендикулярных плоскостям

проекций



A2

B1

A1

B2

j2

Ξ j1

X

A11

A21

IABI

Ось j перпендикулярна горизонтальной плоскости проекций
Точка А движется по окружности, плоскость которой перпендикулярна оси вращения


f

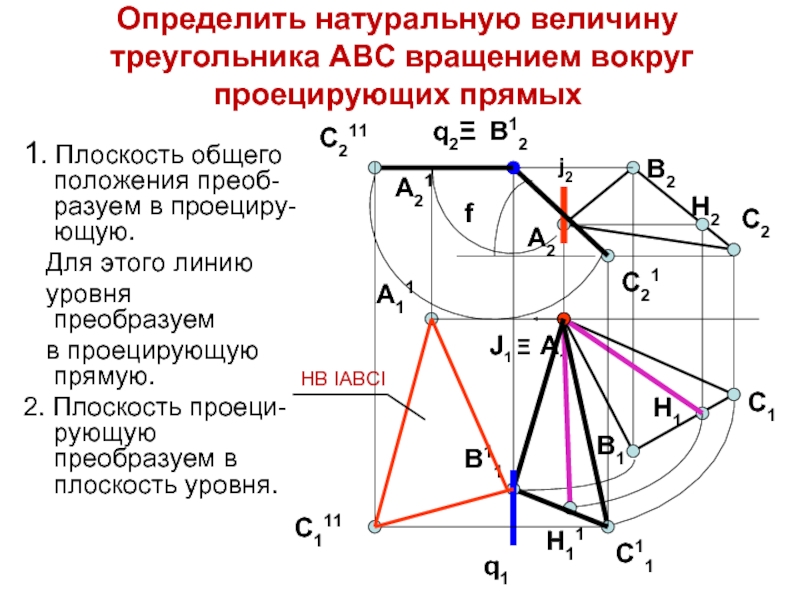
Слайд 221. Плоскость общего положения преоб-разуем в проециру-ющую.
Для этого линию

уровня преобразуем
в проецирующую прямую.
2. Плоскость проеци-рующую преобразуем в плоскость уровня.

Определить натуральную величину треугольника АВС вращением вокруг проецирующих прямых

A1

B2

A2

H1









C1

C2

B1

H2

j2

J1 Ξ






H11


C11


B11


C21

В12


q1

q2Ξ






f

C211

A21



C111

A11

НВ IАВСI

Похожие презентации

Неразъёмные соединения. (Лекция 12) 316
Рабочий чертёж 599
13. Сборочный чертеж 410
Кривые линии 470
ГОСТ 2.305-2008. Изображения на чертежах: виды, разрезы, сечения 600
Эскиз штуцера 879

Обратная связь

Если не удалось найти и скачать презентацию, Вы можете заказать его на нашем сайте. Мы постараемся найти нужный Вам материал и отправим по электронной почте. Не стесняйтесь обращаться к нам, если у вас возникли вопросы или пожелания:

Email: Нажмите что бы посмотреть 

Что такое ThePresentation.ru?

Это сайт презентаций, докладов, проектов, шаблонов в формате PowerPoint. Мы помогаем школьникам, студентам, учителям, преподавателям хранить и обмениваться учебными материалами с другими пользователями.

Для правообладателей

Яндекс.Метрика