- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Сопряжения в черчении презентация
Содержание
- 1. Сопряжения в черчении
- 2. Сопряжением принято называть плавный переход прямой линии
- 3. Сопряжение пересекающихся прямых дугой окружности данного радиуса
- 4. Центр О1 дуги сопряжения находится на пересечении
- 5. Сопряжение дуги окружности и прямой линии дугой
- 6. Сопряжение двух окружностей дугой окружности заданного радиуса
- 7. Сопряжение двух окружностей дугой окружности заданного радиуса
- 8. Сопряжение двух окружностей дугой окружности заданного радиуса
Слайд 2Сопряжением принято называть плавный переход прямой
линии в дугу окружности или одной
этих линий точка называется точкой сопряжения.
В основе алгоритма решения задач на построение сопряжений
лежат следующие правила:
Правило 1. Прямая, касательная к окружности, составляет прямой
угол с радиусом, проведенным в точку касания.
Правило 2. Геометрическим местом центров окружностей,
касательных к данной прямой, является прямая, параллельная
заданной прямой и отстоящая от нее на величину радиуса
окружности.
Правило 3. Точка касания двух окружностей (точка сопряжения)
находится на линии, соединяющей их центры.
Слайд 3Сопряжение пересекающихся прямых дугой окружности данного радиуса
Дано: m, n, R
Решение:
1. В соответствии с правилом 2 проводим
вспомогательные прямые, параллельные заданным m и n,
на расстоянии, равном радиусу R. Точка О пересечения
вспомогательных прямых – центр дуги сопряжения.
2. Точки сопряжения A и B лежат на
перпендикулярах к исходным прямым.
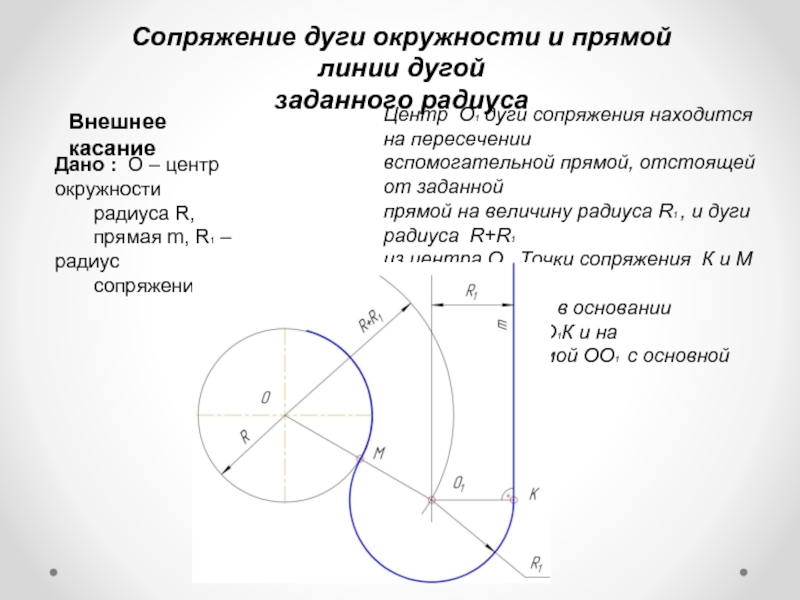
Слайд 4Центр О1 дуги сопряжения находится на пересечении
вспомогательной прямой, отстоящей от заданной
прямой
из центра О. Точки сопряжения К и М находятся
соответственно в основании перпендикуляра О1К и на
пересечении прямой ОО1 с основной окружностью.
Внешнее касание
Дано : О – центр окружности
радиуса R,
прямая m, R1 – радиус
сопряжения
Сопряжение дуги окружности и прямой линии дугой
заданного радиуса
Слайд 5Сопряжение дуги окружности и прямой линии дугой
заданного радиуса
Внутреннее касание
Центр О1
вспомогательной прямой, отстающей от заданной на
величину радиуса R1, и дуги радиуса R-R1 из центра О.
Точки сопряжения – соответственно в основании
перпендикуляра О1 К и на пересечении продолжения луча
ОО1 с основной окружностью.
Дано : О – центр окружности
радиуса R,
прямая m, R1 – радиус
сопряжения
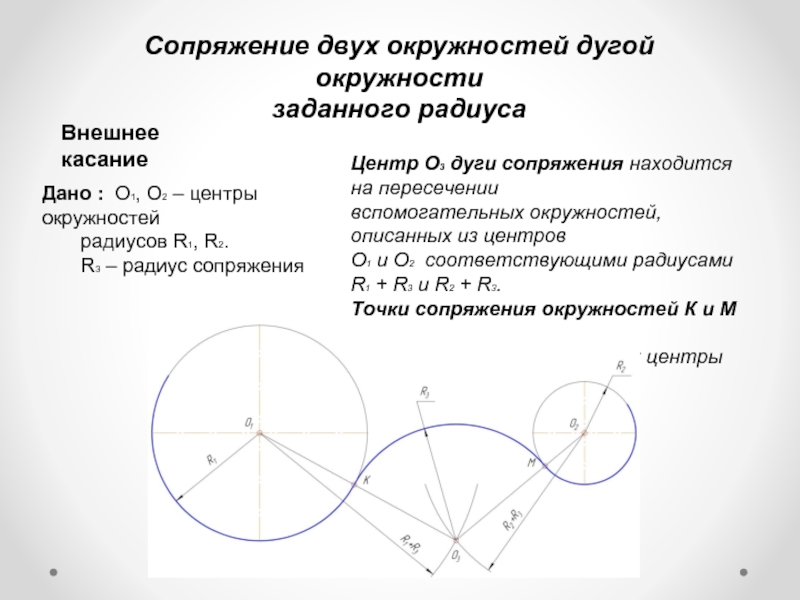
Слайд 6Сопряжение двух окружностей дугой окружности
заданного радиуса
Внешнее касание
Центр О3 дуги сопряжения находится
вспомогательных окружностей, описанных из центров
О1 и О2 соответствующими радиусами R1 + R3 и R2 + R3.
Точки сопряжения окружностей К и М по правилу 3
лежат на лучах, соединяющих центры сопрягаемых
окружностей.
Дано : О1, О2 – центры окружностей
радиусов R1, R2.
R3 – радиус сопряжения
Слайд 7Сопряжение двух окружностей дугой окружности
заданного радиуса
Внутреннее касание
Центр О3 дуги сопряжения находится
вспомогательных окружностей, описанных из центров
О1 и О2 соответствующими радиусами R3 – R1 и R3 – R2.
Точки сопряжения окружностей К и М по правилу 3
лежат на лучах, соединяющих центры сопрягаемых
окружностей.
Дано : О1, О2 – центры окружностей
радиусов R1, R2.
R3 – радиус сопряжения
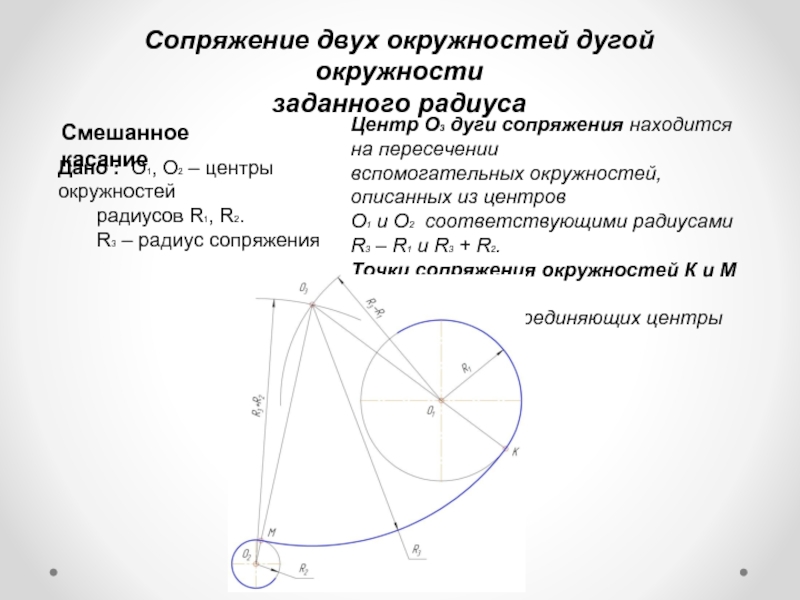
Слайд 8Сопряжение двух окружностей дугой окружности
заданного радиуса
Смешанное касание
Центр О3 дуги сопряжения находится
вспомогательных окружностей, описанных из центров
О1 и О2 соответствующими радиусами R3 – R1 и R3 + R2.
Точки сопряжения окружностей К и М по правилу 3
лежат на лучах, соединяющих центры сопрягаемых
окружностей.
Дано : О1, О2 – центры окружностей
радиусов R1, R2.
R3 – радиус сопряжения