- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Сопряжения. Способы построения сопряжения презентация
Содержание
- 1. Сопряжения. Способы построения сопряжения
- 2. Сопряжением называют плавный переход одной линии в
- 3. Виды сопряжения: Сопряжение двух пересекающихся прямых дугой
- 4. Сопряжение двух пересекающихся прямых дугой заданного радиуса
- 5. Сопряжение двух пересекающихся прямых дугой заданного радиуса
- 6. Сопряжения острого угла.
- 7. Сопряжение окружности и прямой линии дугой заданного
- 8. Сопряжение дуги и прямой линии дугой заданного
- 9. Сопряжения прямой и окружности.
- 10. Сопряжение двух окружностей дугой заданного радиуса. Заданы
- 11. Сопряжение двух окружностей дугой заданного радиуса Внешнее
- 12. Внешнее сопряжение
- 13. Сопряжение двух окружностей дугой заданного радиуса Внутреннее
- 14. Внутренне сопряжения
Слайд 2Сопряжением называют плавный переход одной линии в другую.
Что нужно для
построения сопряжения?
Знать радиус сопряжения (Rc)
Найти центр сопряжения (Ос)
Найти точки сопряжения
Знать радиус сопряжения (Rc)
Найти центр сопряжения (Ос)
Найти точки сопряжения
Слайд 3Виды сопряжения:
Сопряжение двух пересекающихся прямых дугой заданного радиуса.
Сопряжение дуги и прямой
линии дугой заданного радиуса.
Сопряжение двух дуг окружности дугой заданного радиуса.
Сопряжение двух дуг окружности дугой заданного радиуса.
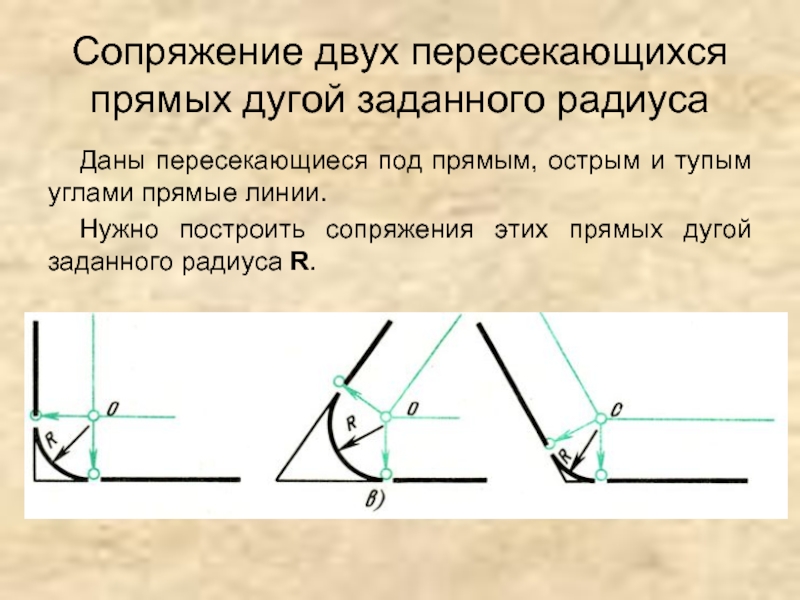
Слайд 4Сопряжение двух пересекающихся прямых дугой заданного радиуса
Даны пересекающиеся под прямым, острым
и тупым углами прямые линии.
Нужно построить сопряжения этих прямых дугой заданного радиуса R.
Нужно построить сопряжения этих прямых дугой заданного радиуса R.
Слайд 5Сопряжение двух пересекающихся прямых дугой заданного радиуса
Проводим вспомогательные прямые параллельно заданным
на расстоянии R от заданных.
Точка пересечения этих прямых будет центром О дуги сопряжения.
Перпендикуляры, опущенные из центра О на заданные прямые, определят точки касания A и B.
Точка пересечения этих прямых будет центром О дуги сопряжения.
Перпендикуляры, опущенные из центра О на заданные прямые, определят точки касания A и B.
Слайд 7Сопряжение окружности и прямой линии дугой заданного радиуса.
Заданы дуга окружности радиусом
R и прямая. Требуется соединить их дугой радиусом r.
Слайд 8Сопряжение дуги и прямой линии дугой заданного радиуса.
Проводим прямую параллельно заданной
на расстоянии r.
Из центра О данной окружности проводим дугу вспомогательной окружности радиусом R+r.
Пересечение прямой и вспомогательной дуги даст точку центра дуги сопряжения О1.
Точка касания дуги и линии D лежит на пересечении перпендикуляра из точки О1 на прямую.
Точка касания дуг E лежит на линии ОО1.
Из центра О данной окружности проводим дугу вспомогательной окружности радиусом R+r.
Пересечение прямой и вспомогательной дуги даст точку центра дуги сопряжения О1.
Точка касания дуги и линии D лежит на пересечении перпендикуляра из точки О1 на прямую.
Точка касания дуг E лежит на линии ОО1.
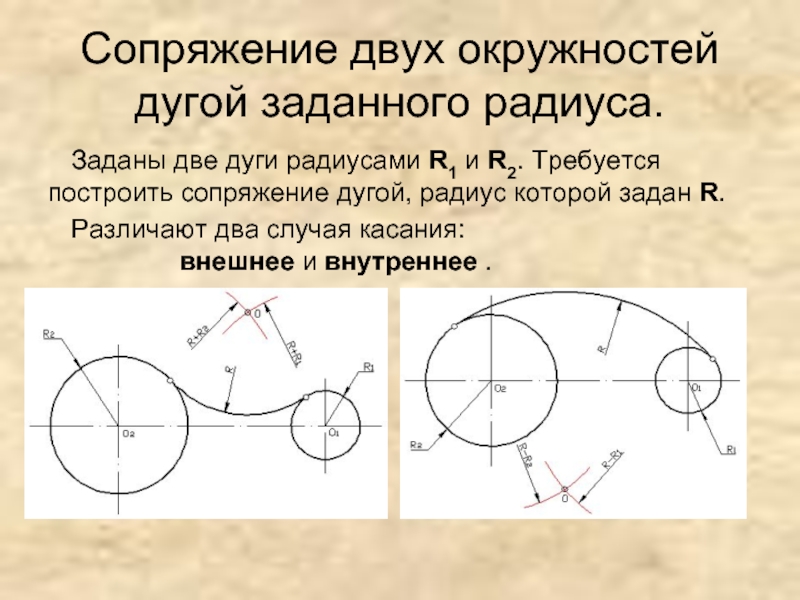
Слайд 10Сопряжение двух окружностей дугой заданного радиуса.
Заданы две дуги радиусами R1 и
R2. Требуется построить сопряжение дугой, радиус которой задан R.
Различают два случая касания: внешнее и внутреннее .
Различают два случая касания: внешнее и внутреннее .
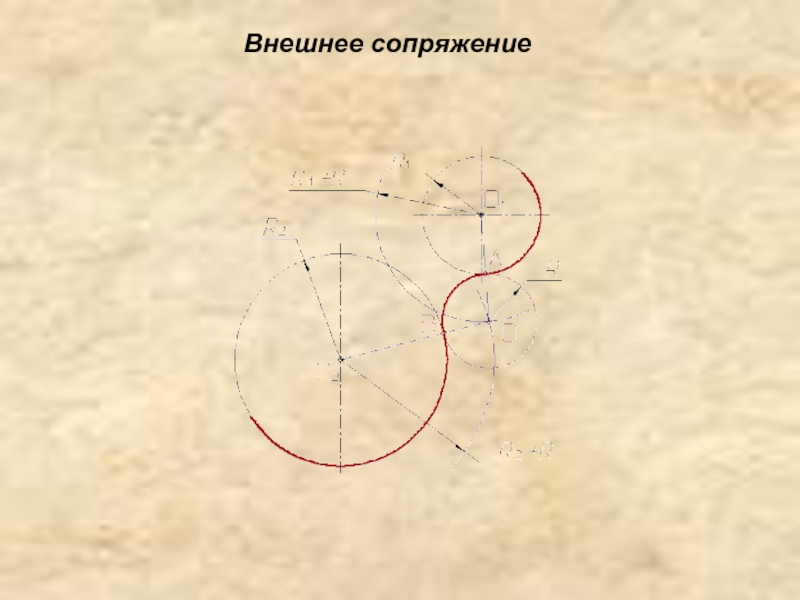
Слайд 11Сопряжение двух окружностей дугой заданного радиуса
Внешнее касание.
Из центра окружности О1 описываем дугу вспомогательной
окружности радиусом R1+R.
Из центра окружности О2 описываем дугу вспомогательной окружности радиусом R2+R.
Пересечение дуг вспомогательных окружностей даст точку О, которая является центром дуги сопряжения (окружности с радиусом R).
Точки касания A и B находятся на линиях ОO1 и ОO2.
Из центра окружности О2 описываем дугу вспомогательной окружности радиусом R2+R.
Пересечение дуг вспомогательных окружностей даст точку О, которая является центром дуги сопряжения (окружности с радиусом R).
Точки касания A и B находятся на линиях ОO1 и ОO2.
Слайд 13Сопряжение двух окружностей дугой заданного радиуса
Внутреннее касание.
Из центра окружности О1 описываем дугу вспомогательной
окружности радиусом R-R1.
Из центра окружности О2 описываем дугу вспомогательной окружности радиусом R-R2.
Пересечение дуг вспомогательных окружностей даст точку О, которая является центром дуги сопряжения (окружности с радиусом R).
Точки сопряжения A и B лежат на продолжении линий ОO1 и ОO2.
Из центра окружности О2 описываем дугу вспомогательной окружности радиусом R-R2.
Пересечение дуг вспомогательных окружностей даст точку О, которая является центром дуги сопряжения (окружности с радиусом R).
Точки сопряжения A и B лежат на продолжении линий ОO1 и ОO2.
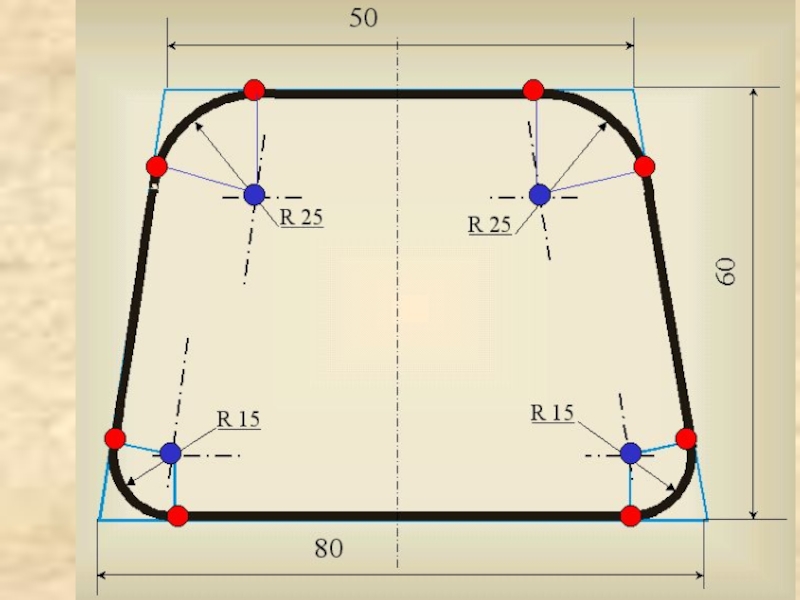
Слайд 15
R 25
R 25
R 15
R 15
80
50
60
А теперь для закрепления материала выполним практическое
задание:
«Построить сопряжения в заданной фигуре».
Выполняется в тетради с предварительным разбором и демонстрацией.
«Построить сопряжения в заданной фигуре».
Выполняется в тетради с предварительным разбором и демонстрацией.