Решение позиционных задач презентация

Содержание

1. Решение позиционных задач
2. 2. Пересечение геометрических объектов общего положения 2.1.
3. 2.1. Алгоритм способа вспомогательных секущих поверхностей 1.
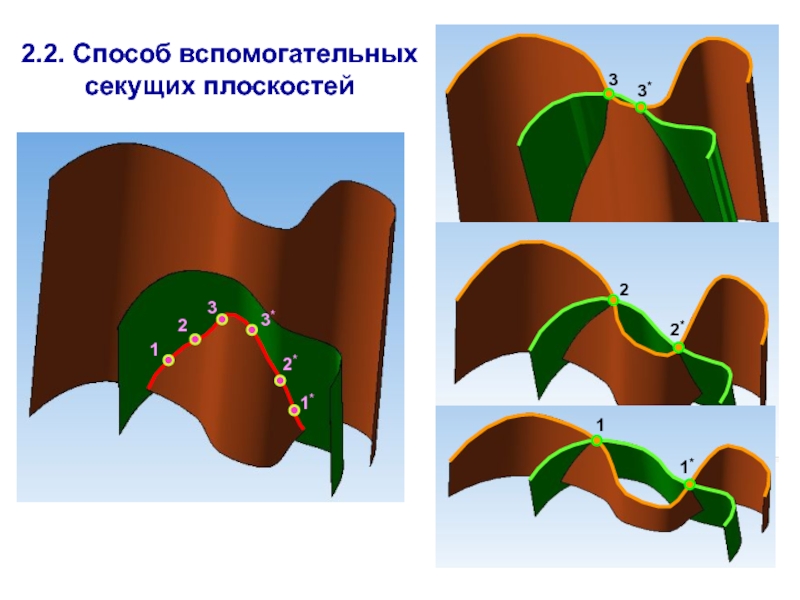
4. 2.2. Способ вспомогательных секущих плоскостей
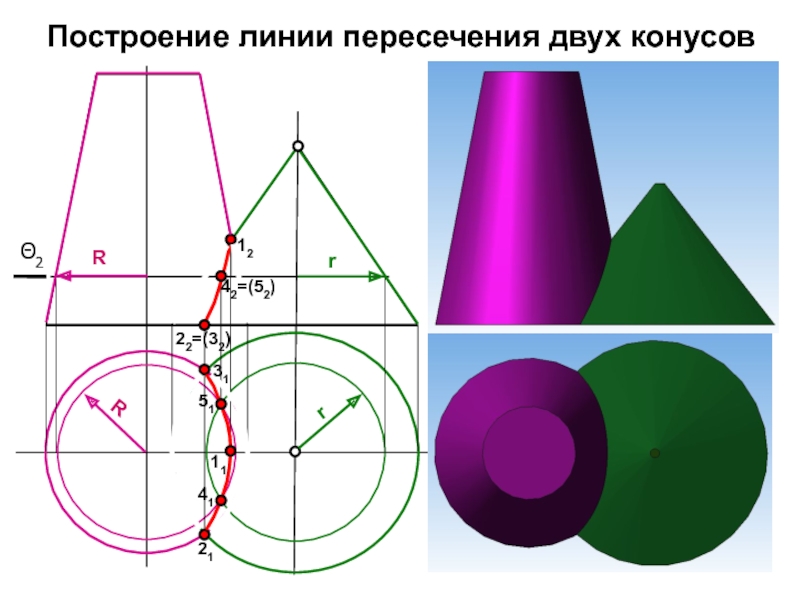
5. Построение линии пересечения двух конусов
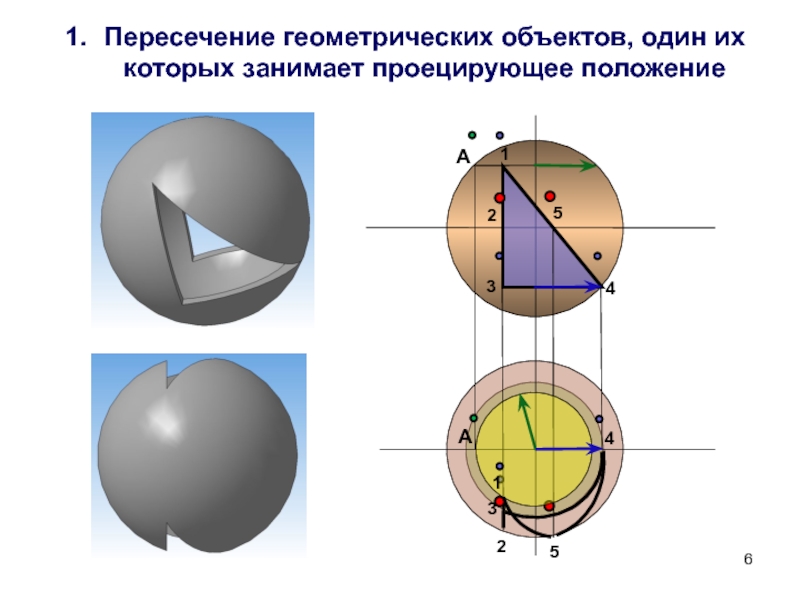
6. Пересечение геометрических объектов, один их которых
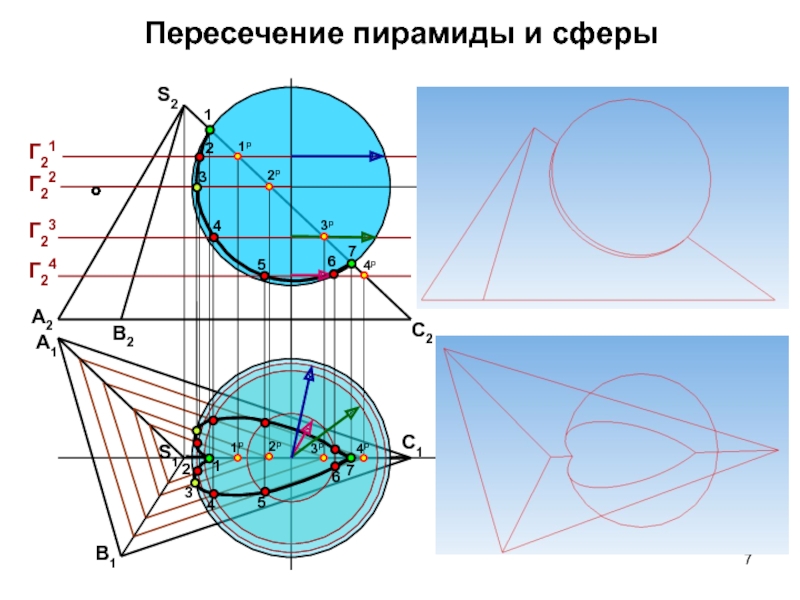
7. Пересечение пирамиды и сферы
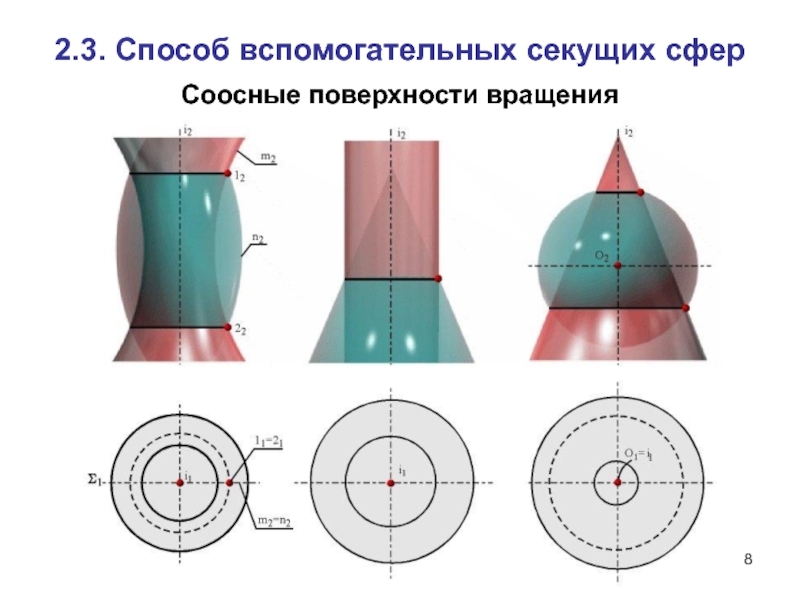
8. Соосные поверхности вращения 2.3. Способ вспомогательных секущих сфер
9. Пересечение сферы поверхностями вращения Линия пересечения поверхностей
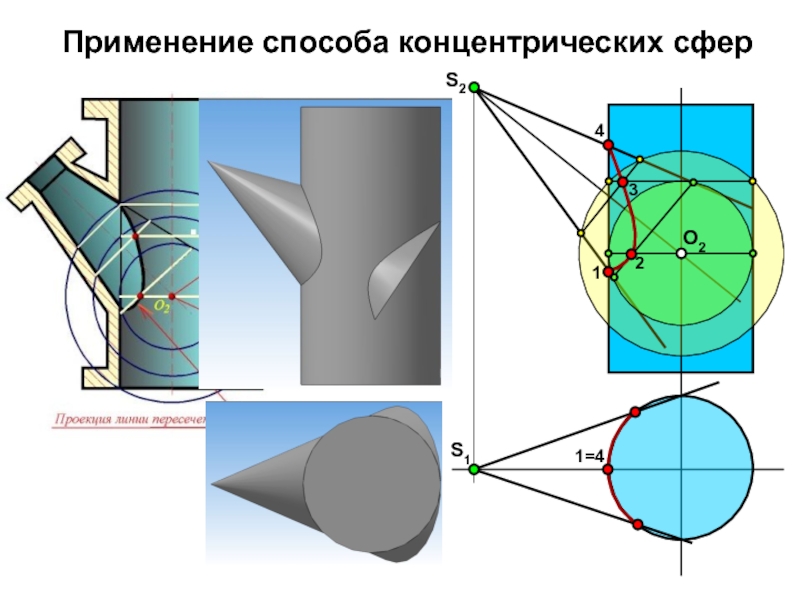
10. Применение способа концентрических сфер
11. 2.4. Теорема Монжа Если две поверхности второго
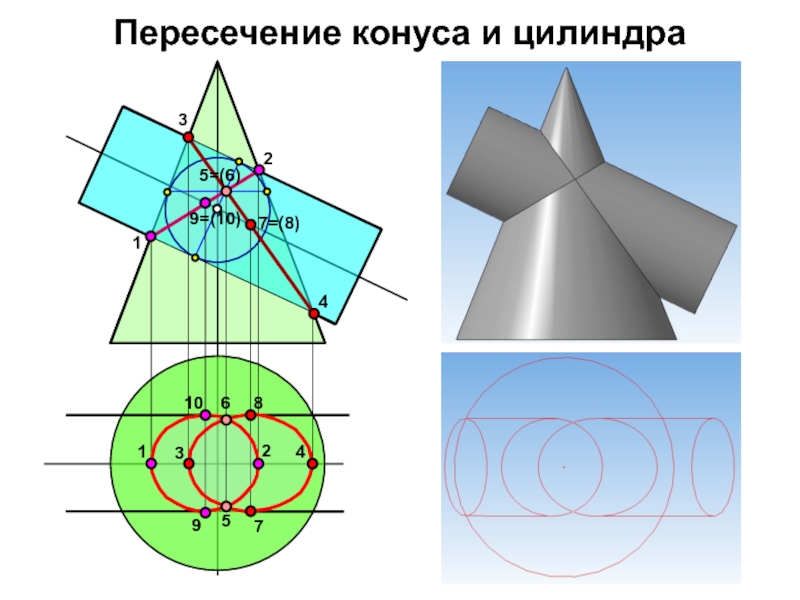
12. Пересечение конуса и цилиндра

2. Пересечение геометрических объектов общего положения 2.1. Общий алгоритм способа вспомогательных секущих поверхностей. 2.2. Способ вспомогательных секущих плоскостей. 2.3. Способ вспомогательных секущих сфер. 2.4. Теорема Монжа.

Главная
Графика
Решение позиционных задач

Слайд 1Тема 3. Решение позиционных задач
Пересечение геометрических объектов, один их которых занимает

проецирующее положение.

2. Пересечение геометрических объектов общего положения.

Слайд 22. Пересечение геометрических объектов общего положения
2.1. Общий алгоритм способа вспомогательных секущих

поверхностей.
2.2. Способ вспомогательных секущих плоскостей.
2.3. Способ вспомогательных секущих сфер.
2.4. Теорема Монжа.

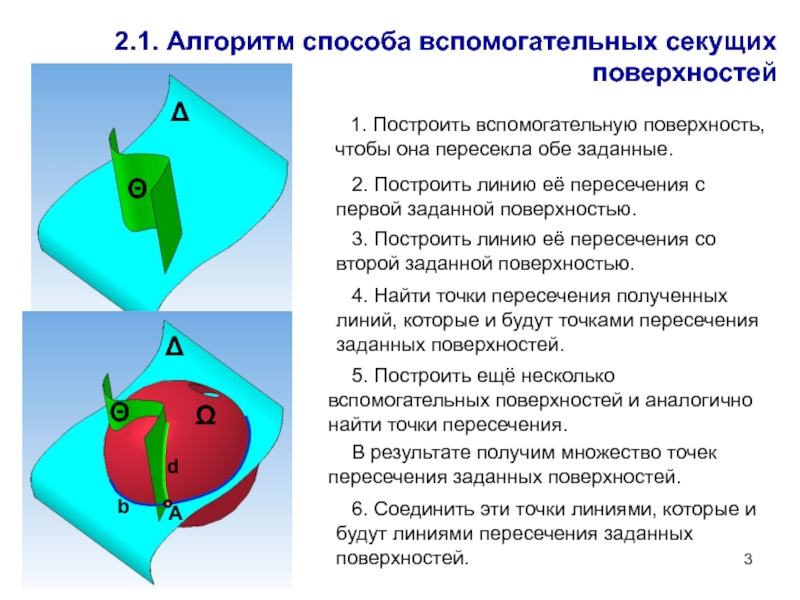
Слайд 32.1. Алгоритм способа вспомогательных секущих поверхностей
1. Построить вспомогательную поверхность, чтобы она

пересекла обе заданные.

2. Построить линию её пересечения с первой заданной поверхностью.

3. Построить линию её пересечения со второй заданной поверхностью.

4. Найти точки пересечения полученных линий, которые и будут точками пересечения заданных поверхностей.

5. Построить ещё несколько вспомогательных поверхностей и аналогично найти точки пересечения.
В результате получим множество точек пересечения заданных поверхностей.

6. Соединить эти точки линиями, которые и будут линиями пересечения заданных поверхностей.

Слайд 42.2. Способ вспомогательных секущих плоскостей

1
2
2*
1*
3*
3
1
2
2*
1*
3*
3

Слайд 5Построение линии пересечения двух конусов

Θ2

12
42=(52)
22=(32)
11
21
31
41
51

R
R
r
r

Слайд 6
Пересечение геометрических объектов, один их которых занимает проецирующее положение

1
2
3
4
5
A
A
1
2
4
5
3

Слайд 7Пересечение пирамиды и сферы

Г21

А2
В2
С2
S2
А1
В1
С1
S1
1
2
3
4
5
6
7
1
2
3
4
5
6
7
1р
2р
3р
4р
1р
2р
3р
4р
Г22
Г23
Г24

Слайд 8Соосные поверхности вращения
2.3. Способ вспомогательных секущих сфер

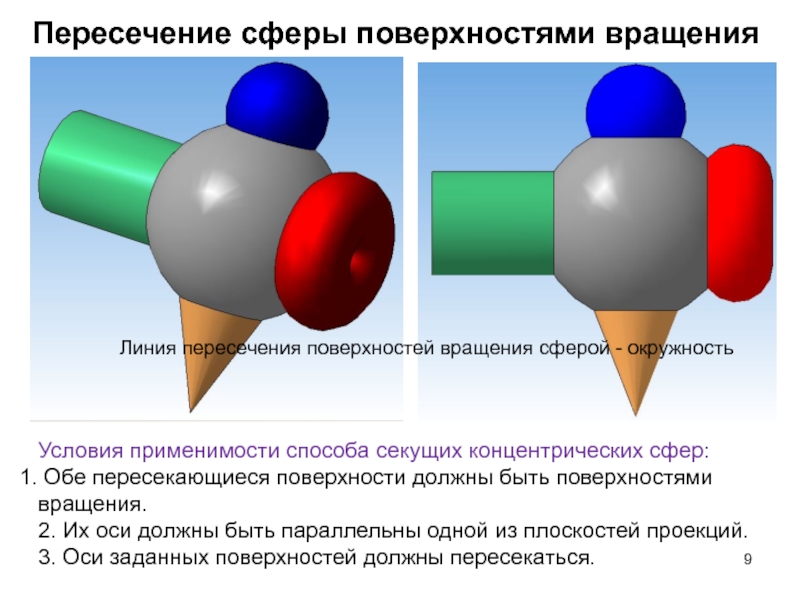
Слайд 9Пересечение сферы поверхностями вращения
Линия пересечения поверхностей вращения сферой - окружность
Условия применимости

способа секущих концентрических сфер:
Обе пересекающиеся поверхности должны быть поверхностями вращения.
2. Их оси должны быть параллельны одной из плоскостей проекций.
3. Оси заданных поверхностей должны пересекаться.

Слайд 10Применение способа концентрических сфер

S2
S1

О2
1
2
3
4
1=4

Слайд 112.4. Теорема Монжа
Если две поверхности второго порядка описаны около третьей поверхности

(или вписаны в неё), то линия их пересечения распадается на две кривые второго порядка (эллипс, окружность, гиперболу, параболу). Причём плоскости этих кривых проходят через прямую, соединяющую точки пересечения линии касания.

Слайд 12Пересечение конуса и цилиндра

1
2
3
4
5=(6)
9=(10)
7=(8)
1
2
3
4
5
6
10
7
9
8

Скачать презентацию

Решение позиционных задач презентация

Содержание

Слайд 1Тема 3. Решение позиционных задач
Пересечение геометрических объектов, один их которых занимает

Слайд 22. Пересечение геометрических объектов общего положения
2.1. Общий алгоритм способа вспомогательных секущих

Слайд 32.1. Алгоритм способа вспомогательных секущих поверхностей
1. Построить вспомогательную поверхность, чтобы она

Слайд 42.2. Способ вспомогательных секущих плоскостей

1
2
2*
1*
3*
3
1
2
2*
1*
3*
3

Слайд 5Построение линии пересечения двух конусов

Θ2

12
42=(52)
22=(32)
11
21
31
41
51

R
R
r
r

Слайд 6
Пересечение геометрических объектов, один их которых занимает проецирующее положение

1
2
3
4
5
A
A
1
2
4
5
3

Слайд 7Пересечение пирамиды и сферы

Г21

А2
В2
С2
S2
А1
В1
С1
S1
1
2
3
4
5
6
7
1
2
3
4
5
6
7
1р
2р
3р
4р
1р
2р
3р
4р
Г22
Г23
Г24

Слайд 8Соосные поверхности вращения
2.3. Способ вспомогательных секущих сфер

Слайд 9Пересечение сферы поверхностями вращения
Линия пересечения поверхностей вращения сферой - окружность
Условия применимости

Слайд 10Применение способа концентрических сфер

S2
S1

О2
1
2
3
4
1=4

Слайд 112.4. Теорема Монжа
Если две поверхности второго порядка описаны около третьей поверхности

Слайд 12Пересечение конуса и цилиндра

1
2
3
4
5=(6)
9=(10)
7=(8)
1
2
3
4
5
6
10
7
9
8

Обратная связь

Что такое ThePresentation.ru?

Решение позиционных задач презентация

Содержание

Слайд 1Тема 3. Решение позиционных задачПересечение геометрических объектов, один их которых занимает

Слайд 22. Пересечение геометрических объектов общего положения2.1. Общий алгоритм способа вспомогательных секущих

Слайд 32.1. Алгоритм способа вспомогательных секущих поверхностей1. Построить вспомогательную поверхность, чтобы она

Слайд 42.2. Способ вспомогательных секущих плоскостей122*1*3*3122*1*3*3

Слайд 5Построение линии пересечения двух конусовΘ21242=(52)22=(32)1121314151RRrr

Слайд 6Пересечение геометрических объектов, один их которых занимает проецирующее положение 12345AA12453

Слайд 7Пересечение пирамиды и сферыГ21А2В2С2S2А1В1С1S1123456712345671р2р3р4р1р2р3р4рГ22Г23Г24

Слайд 8Соосные поверхности вращения2.3. Способ вспомогательных секущих сфер

Слайд 9Пересечение сферы поверхностями вращенияЛиния пересечения поверхностей вращения сферой - окружностьУсловия применимости

Слайд 10Применение способа концентрических сфер S2S1О212341=4

Слайд 112.4. Теорема МонжаЕсли две поверхности второго порядка описаны около третьей поверхности

Слайд 12Пересечение конуса и цилиндра12345=(6)9=(10)7=(8)12345610798

Похожие презентации

Обратная связь

Что такое ThePresentation.ru?

Слайд 1Тема 3. Решение позиционных задач
Пересечение геометрических объектов, один их которых занимает

Слайд 22. Пересечение геометрических объектов общего положения
2.1. Общий алгоритм способа вспомогательных секущих

Слайд 32.1. Алгоритм способа вспомогательных секущих поверхностей
1. Построить вспомогательную поверхность, чтобы она

Слайд 42.2. Способ вспомогательных секущих плоскостей

1
2
2*
1*
3*
3
1
2
2*
1*
3*
3

Слайд 5Построение линии пересечения двух конусов

Θ2

12
42=(52)
22=(32)
11
21
31
41
51

R
R
r
r

Слайд 6
Пересечение геометрических объектов, один их которых занимает проецирующее положение

1
2
3
4
5
A
A
1
2
4
5
3

Слайд 7Пересечение пирамиды и сферы

Г21

А2
В2
С2
S2
А1
В1
С1
S1
1
2
3
4
5
6
7
1
2
3
4
5
6
7
1р
2р
3р
4р
1р
2р
3р
4р
Г22
Г23
Г24

Слайд 8Соосные поверхности вращения
2.3. Способ вспомогательных секущих сфер

Слайд 9Пересечение сферы поверхностями вращения
Линия пересечения поверхностей вращения сферой - окружность
Условия применимости

Слайд 10Применение способа концентрических сфер

S2
S1

О2
1
2
3
4
1=4

Слайд 112.4. Теорема Монжа
Если две поверхности второго порядка описаны около третьей поверхности

Слайд 12Пересечение конуса и цилиндра

1
2
3
4
5=(6)
9=(10)
7=(8)
1
2
3
4
5
6
10
7
9
8