Развертки поверхностей презентация

Содержание

1. Развертки поверхностей
2. http://www.verteco.ru/projects/?tag=1&val=2008 http://www.breezair.ucoz.ru/photo/1-0-114-3 http://www.prodayslona.ru/catalog/adds/element/82871/ http://www.vip-express.ru/gallery/angar_galery.html Тентовые сооружения
3. http://www.ua.all-biz.info/regions/index.php?fuseaction=adm_enterprises.catalogProducts&rgn_id=14&cs=50&page=3 http://www.ua.all-biz.info/buy/goods/?group=1000551&cid=210891 http://www.tctena.ru/catalog.php?comp_id=10 Резервуары воздуховоды шаровый каплевидный
5. Основные свойства разверток 1. Длины линий на
6. 3. Прямые, параллельные на поверхности, остаются параллельными
7. 5. Прямая линия на поверхности переходит в
8. К числу развертывающихся поверхностей относятся многогранные поверхности; из линейчатых – цилиндрические, конические, торсовые
9. По возможностям и способам построения различают развертки
10. S2 A2 B2
11. Способ нормального сечения
12. Приближенные развертки Способ треугольников (триангуляции) Сущность способа
13. S2 S1
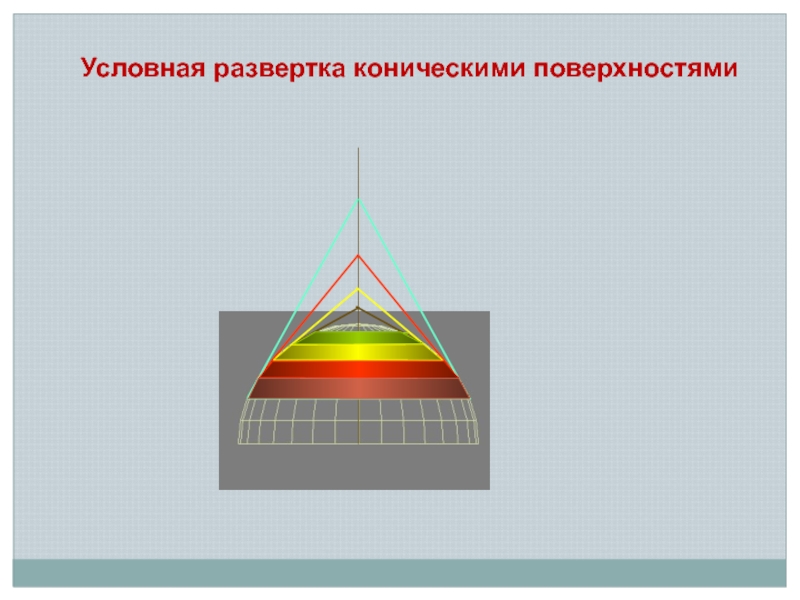
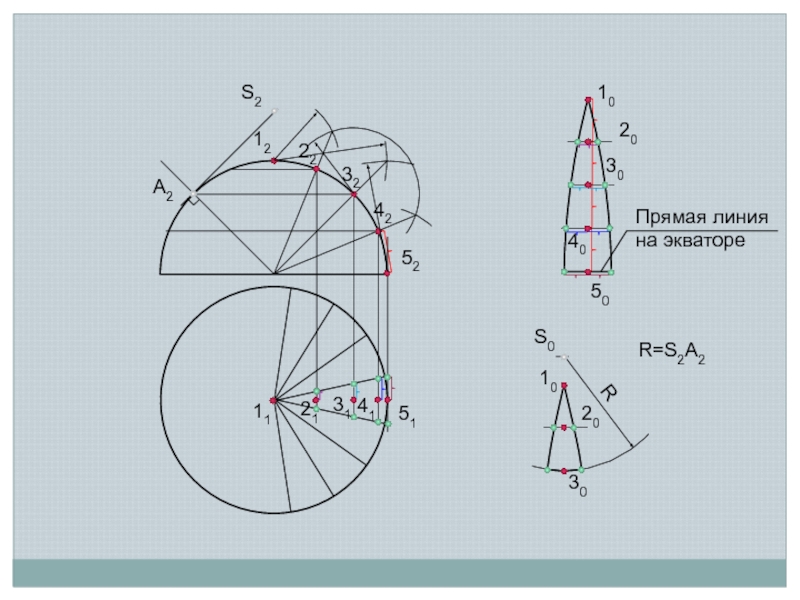
14. Условная развертка на основе аппроксимации цилиндрическими или коническими поверхностями
15. Условная развертка коническими поверхностями
16. Условная развертка цилиндрическими поверхностями

http://www.verteco.ru/projects/?tag=1&val=2008 http://www.breezair.ucoz.ru/photo/1-0-114-3 http://www.prodayslona.ru/catalog/adds/element/82871/ http://www.vip-express.ru/gallery/angar_galery.html Тентовые сооружения

Главная
Графика
Развертки поверхностей

Слайд 1РАЗВЕРТКИ ПОВЕРХНОСТЕЙ

Слайд 2http://www.verteco.ru/projects/?tag=1&val=2008
http://www.breezair.ucoz.ru/photo/1-0-114-3
http://www.prodayslona.ru/catalog/adds/element/82871/
http://www.vip-express.ru/gallery/angar_galery.html
Тентовые сооружения

Слайд 3http://www.ua.all-biz.info/regions/index.php?fuseaction=adm_enterprises.catalogProducts&rgn_id=14&cs=50&page=3
http://www.ua.all-biz.info/buy/goods/?group=1000551&cid=210891
http://www.tctena.ru/catalog.php?comp_id=10
Резервуары
воздуховоды
шаровый
каплевидный

Слайд 4

ϕ
ϕо

Fо
F
A
B
Bo
Ao
ℓo
ℓ
f
fo
Co
Do
C
D

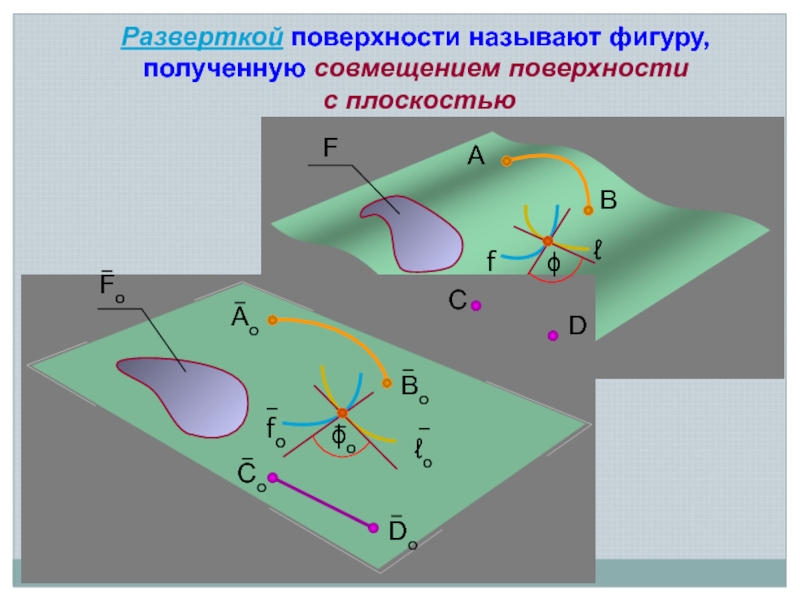
Разверткой поверхности называют фигуру, полученную совмещением поверхности
с плоскостью

Слайд 5Основные свойства разверток
1. Длины линий на поверхности и на развертке одинаковы
2.

Углы между обыкновенными линиями на поверхности равны соответствующим углам на развертке

Углом между линиями называют угол, образованный их касательными, проведенными в точке пересечения линий

Преобразование, в котором сохраняется равенство углов называется конформным Поэтому поверхность и развертка конформны

Слайд 63. Прямые, параллельные на поверхности, остаются параллельными и на развертке Это

вытекает из второго свойства

4. Площади, ограниченные замкнутой линией на поверхности и на развертке равны Преобразование, в котором сохраняется равенство площадей, называют эквиареальным

Слайд 75. Прямая линия на поверхности переходит в прямую линию на развертке
6.

Прямая линия между двумя точками на развертке соответствует кратчайшему расстоянию между этими точками на поверхности

Эти линии на поверхности называют геодезическими линиями

Поверхности, для которых сохраняются указанные свойства на развертке, называют развертывающимися

Слайд 8К числу развертывающихся поверхностей относятся многогранные поверхности;
из линейчатых – цилиндрические,

конические, торсовые

Слайд 9По возможностям и способам построения различают развертки
точные, приближенные и условные
Точными называют

развертки, построенные с применением математического аппарата, и развертки многогранных поверхностей

Условные развертки неразвертывающихся поверхностей строят способом цилиндров и конусов

Приближенными – развертки, построенные способом вписанных или описанных многогранных поверхностей

Слайд 10

S2
A2
B2

S1
ℓ

ϕ =180 – [град]
D
ℓ
S0

ϕ

A0
B0
A0
B0
Точные развертки
B1

A1

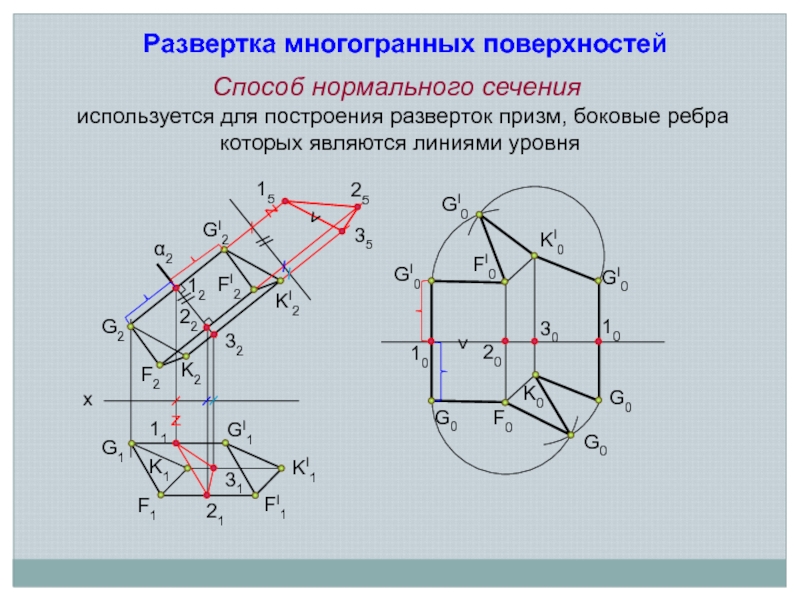
Слайд 11Способ нормального сечения

G2
F2
K2
KI1
FI1
GI1

x

α2

11
21
31
32
22
12

z
z

15
25
35
K0
F0
G0
G0

G0

KI2
FI2
GI2
GI0
GI0
GI0
FI0
KI0

Развертка многогранных поверхностей
используется для построения разверток призм, боковые ребра

которых являются линиями уровня

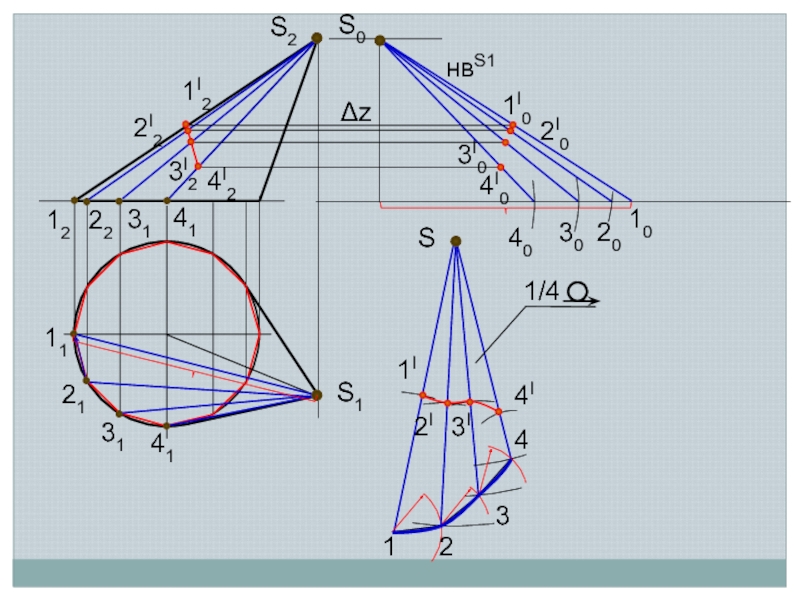
Слайд 12Приближенные развертки
Способ треугольников (триангуляции)
Сущность способа заключается в том, что кривую линейчатую

поверхность заменяют вписанной в нее многогранной поверхностью с треугольными гранями, нахождению натурального вида многогранной поверхности
и последовательному построению
на чертеже

Слайд 13S2
S1

11
21
31
41
12
22
31
41

Δz

S0
10
20
30
40
4
3
2
1

S
нвS1

1/4

4I0
3I0
1I0
2I0
4I2
1I2
2I2
3I2
1I
2I
3I
4I

Слайд 14 Условная развертка на основе аппроксимации цилиндрическими или коническими поверхностями

Слайд 15 Условная развертка коническими поверхностями

Слайд 16 Условная развертка цилиндрическими поверхностями

Слайд 17

51
41
31
21
11
52
42
32
22
12
50
40
30
20
10

30
20
10

S0
S2

R
A2
R=S2A2

Прямая линия на экваторе

Скачать презентацию

Развертки поверхностей презентация

Содержание

Слайд 1РАЗВЕРТКИ ПОВЕРХНОСТЕЙ

Слайд 2http://www.verteco.ru/projects/?tag=1&val=2008
http://www.breezair.ucoz.ru/photo/1-0-114-3
http://www.prodayslona.ru/catalog/adds/element/82871/
http://www.vip-express.ru/gallery/angar_galery.html
Тентовые сооружения

Слайд 4

ϕ
ϕо

Fо
F
A
B
Bo
Ao
ℓo
ℓ
f
fo
Co
Do
C
D

Разверткой поверхности называют фигуру, полученную совмещением поверхности
с плоскостью

Слайд 5Основные свойства разверток
1. Длины линий на поверхности и на развертке одинаковы
2.

Слайд 63. Прямые, параллельные на поверхности, остаются параллельными и на развертке Это

Слайд 75. Прямая линия на поверхности переходит в прямую линию на развертке
6.

Слайд 8К числу развертывающихся поверхностей относятся многогранные поверхности;
из линейчатых – цилиндрические,

Слайд 9По возможностям и способам построения различают развертки
точные, приближенные и условные
Точными называют

Слайд 10

S2
A2
B2

S1
ℓ

ϕ =180 – [град]
D
ℓ
S0

ϕ

A0
B0
A0
B0
Точные развертки
B1

A1

Слайд 12Приближенные развертки
Способ треугольников (триангуляции)
Сущность способа заключается в том, что кривую линейчатую

Слайд 13S2
S1

11
21
31
41
12
22
31
41

Δz

S0
10
20
30
40
4
3
2
1

S
нвS1

1/4

4I0
3I0
1I0
2I0
4I2
1I2
2I2
3I2
1I
2I
3I
4I

Слайд 14 Условная развертка на основе аппроксимации цилиндрическими или коническими поверхностями

Слайд 15 Условная развертка коническими поверхностями

Слайд 16 Условная развертка цилиндрическими поверхностями

Слайд 17

51
41
31
21
11
52
42
32
22
12
50
40
30
20
10

30
20
10

S0
S2

R
A2
R=S2A2

Прямая линия на экваторе

Обратная связь

Что такое ThePresentation.ru?

Развертки поверхностей презентация

Содержание

Слайд 1РАЗВЕРТКИ ПОВЕРХНОСТЕЙ

Слайд 2http://www.verteco.ru/projects/?tag=1&val=2008http://www.breezair.ucoz.ru/photo/1-0-114-3http://www.prodayslona.ru/catalog/adds/element/82871/http://www.vip-express.ru/gallery/angar_galery.htmlТентовые сооружения

Слайд 4ϕϕоFоFABBoAoℓoℓffoCoDoCDРазверткой поверхности называют фигуру, полученную совмещением поверхности с плоскостью

Слайд 5Основные свойства разверток1. Длины линий на поверхности и на развертке одинаковы2.

Слайд 63. Прямые, параллельные на поверхности, остаются параллельными и на развертке Это

Слайд 75. Прямая линия на поверхности переходит в прямую линию на развертке6.

Слайд 8К числу развертывающихся поверхностей относятся многогранные поверхности; из линейчатых – цилиндрические,

Слайд 9По возможностям и способам построения различают разверткиточные, приближенные и условныеТочными называют

Слайд 10S2A2B2S1ℓϕ =180 – [град]DℓS0ϕA0B0A0B0Точные разверткиB1A1

Слайд 12Приближенные разверткиСпособ треугольников (триангуляции)Сущность способа заключается в том, что кривую линейчатую

Слайд 13S2S11121314112223141ΔzS0102030404321SнвS11/44I03I01I02I04I21I22I23I21I2I3I4I

Слайд 14 Условная развертка на основе аппроксимации цилиндрическими или коническими поверхностями

Слайд 15 Условная развертка коническими поверхностями

Слайд 16 Условная развертка цилиндрическими поверхностями

Слайд 17514131211152423222125040302010302010S0S2RA2R=S2A2Прямая линия на экваторе

Похожие презентации

Обратная связь

Что такое ThePresentation.ru?

Слайд 2http://www.verteco.ru/projects/?tag=1&val=2008
http://www.breezair.ucoz.ru/photo/1-0-114-3
http://www.prodayslona.ru/catalog/adds/element/82871/
http://www.vip-express.ru/gallery/angar_galery.html
Тентовые сооружения

Слайд 4

ϕ
ϕо

Fо
F
A
B
Bo
Ao
ℓo
ℓ
f
fo
Co
Do
C
D

Разверткой поверхности называют фигуру, полученную совмещением поверхности
с плоскостью

Слайд 5Основные свойства разверток
1. Длины линий на поверхности и на развертке одинаковы
2.

Слайд 75. Прямая линия на поверхности переходит в прямую линию на развертке
6.

Слайд 8К числу развертывающихся поверхностей относятся многогранные поверхности;
из линейчатых – цилиндрические,

Слайд 9По возможностям и способам построения различают развертки
точные, приближенные и условные
Точными называют

Слайд 10

S2
A2
B2

S1
ℓ

ϕ =180 – [град]
D
ℓ
S0

ϕ

A0
B0
A0
B0
Точные развертки
B1

A1

Слайд 12Приближенные развертки
Способ треугольников (триангуляции)
Сущность способа заключается в том, что кривую линейчатую

Слайд 13S2
S1

11
21
31
41
12
22
31
41

Δz

S0
10
20
30
40
4
3
2
1

S
нвS1

1/4

4I0
3I0
1I0
2I0
4I2
1I2
2I2
3I2
1I
2I
3I
4I

Слайд 17

51
41
31
21
11
52
42
32
22
12
50
40
30
20
10

30
20
10

S0
S2

R
A2
R=S2A2

Прямая линия на экваторе