- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Прямая в системе H, V, W (Лекция 2) презентация
Содержание
- 1. Прямая в системе H, V, W (Лекция 2)
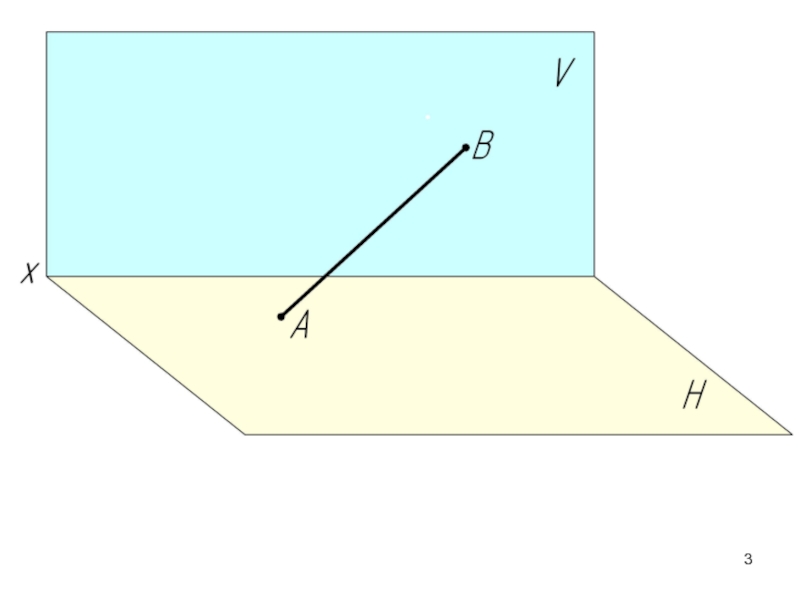
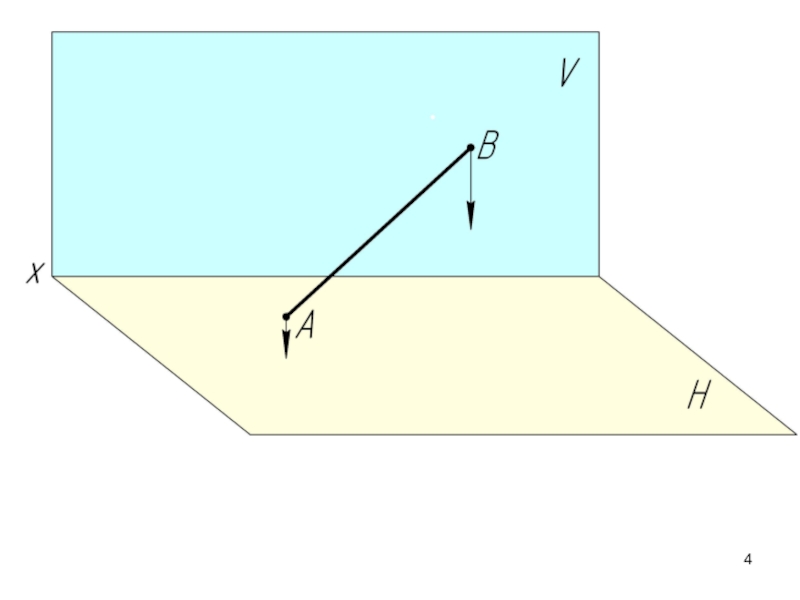
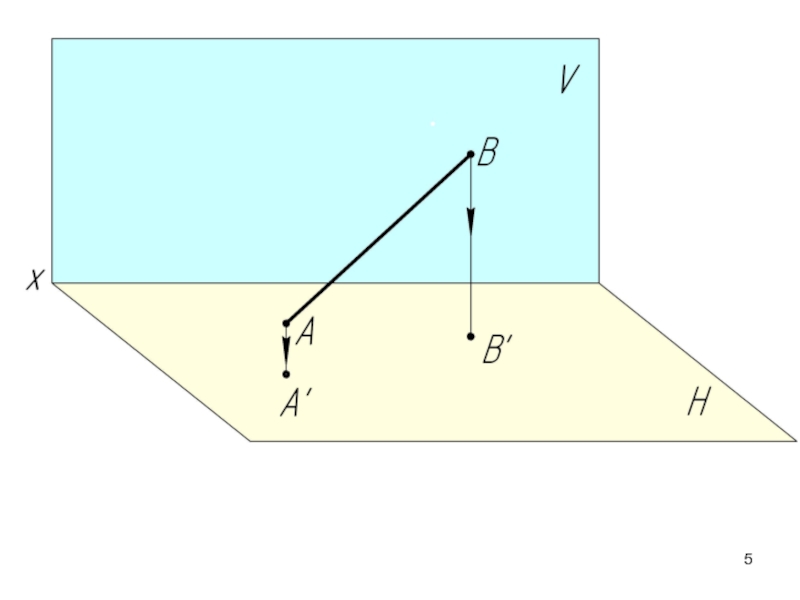
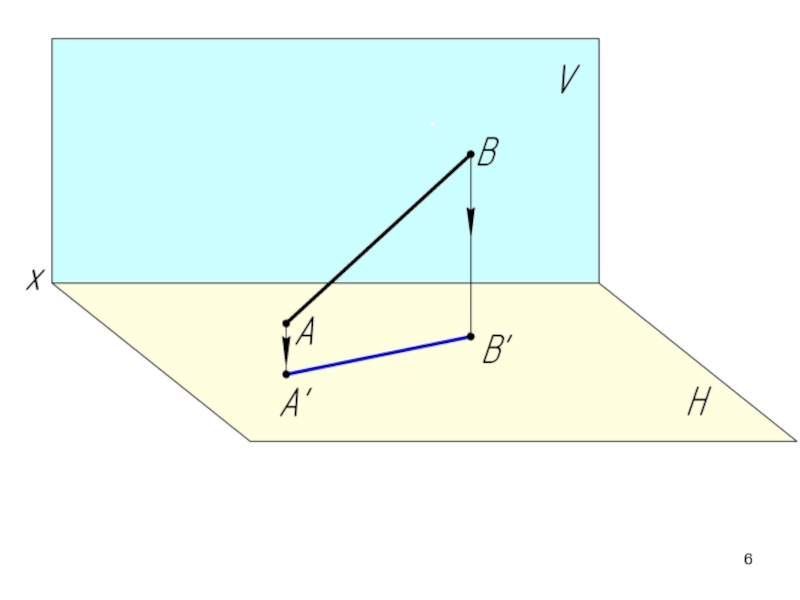
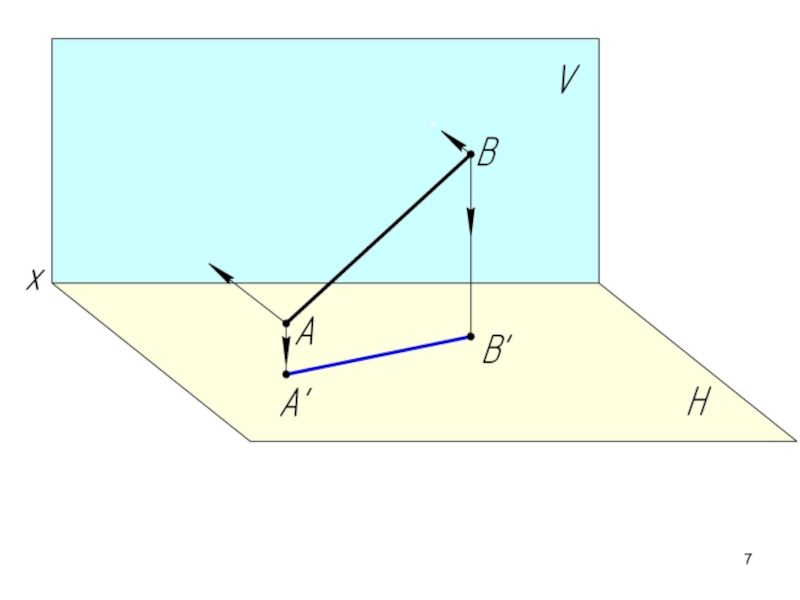
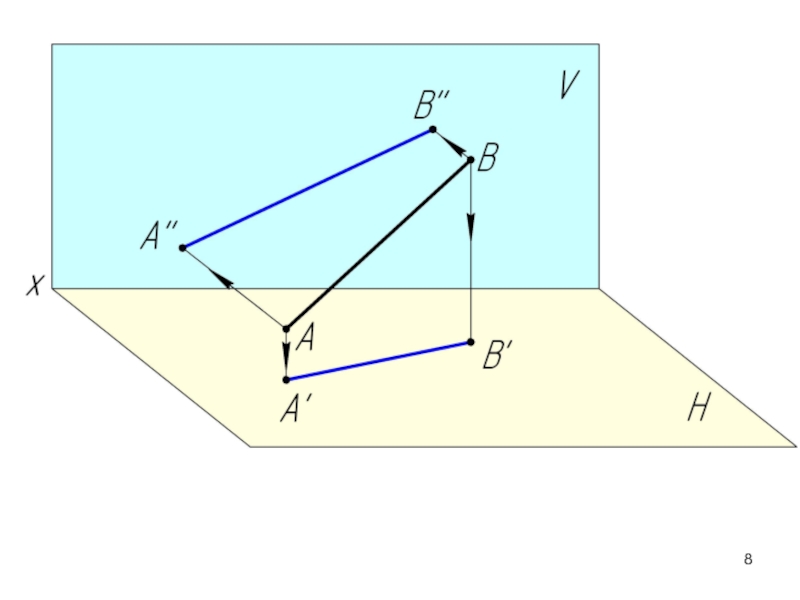
- 2. 2.1. Проекции прямой. Принадлежность точки прямой.
- 16. Если точка принадлежит прямой, то ее проекции
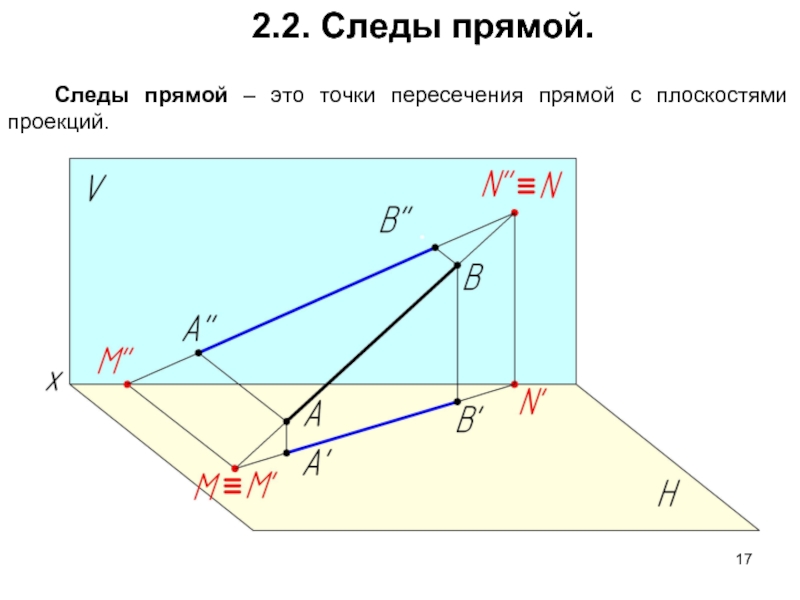
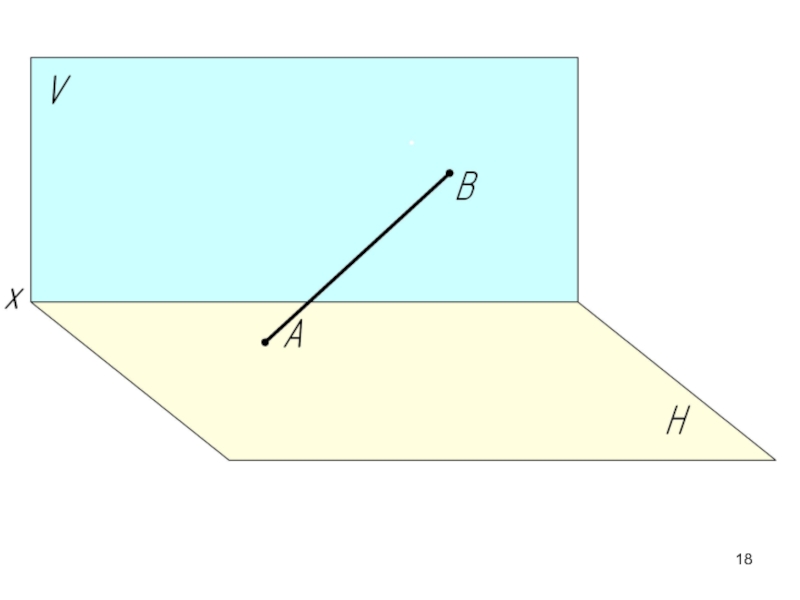
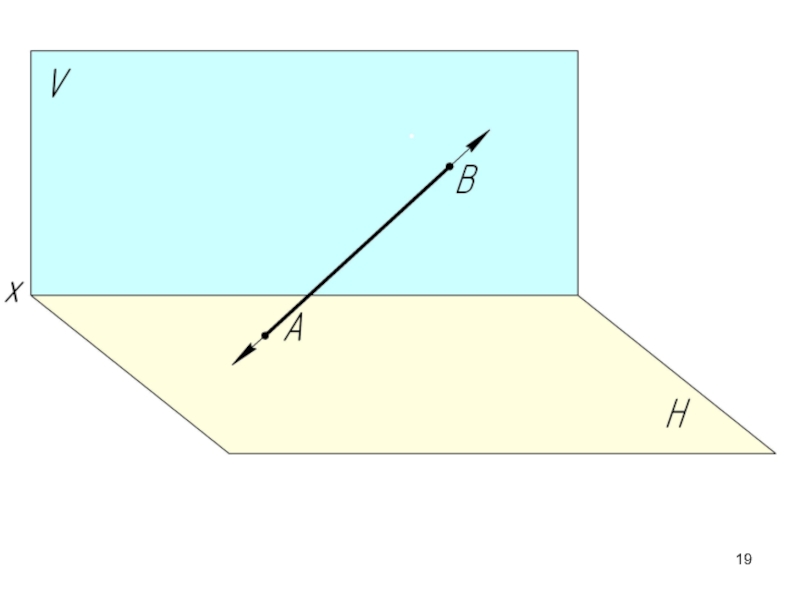
- 17. 2.2. Следы прямой. Следы прямой –
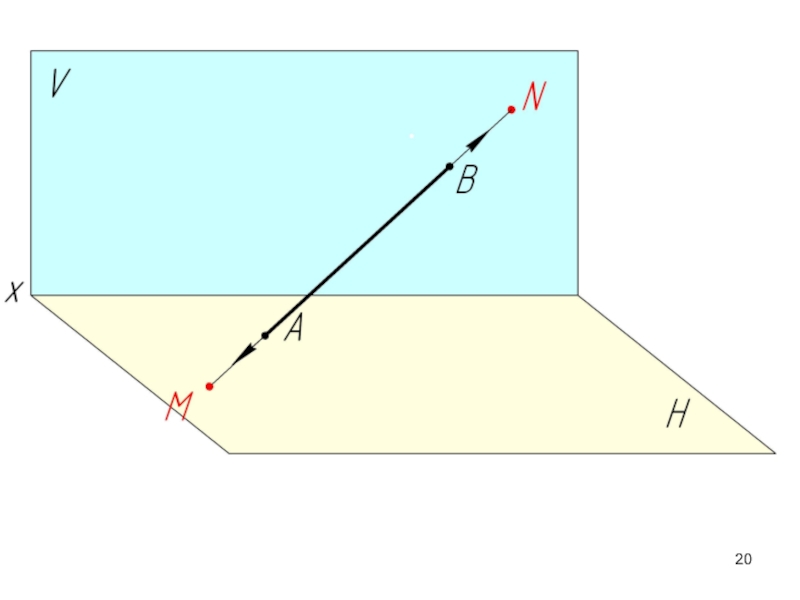
- 23. М – горизонтальный след прямой АВ;
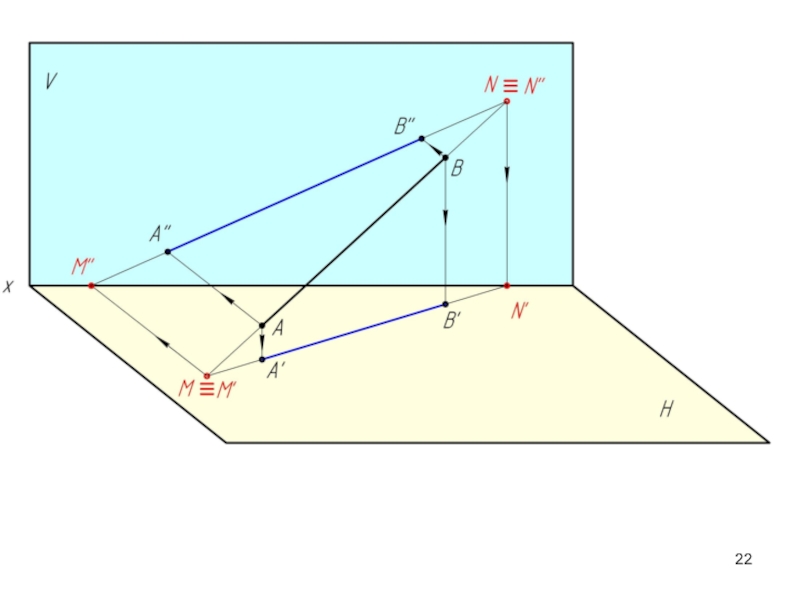
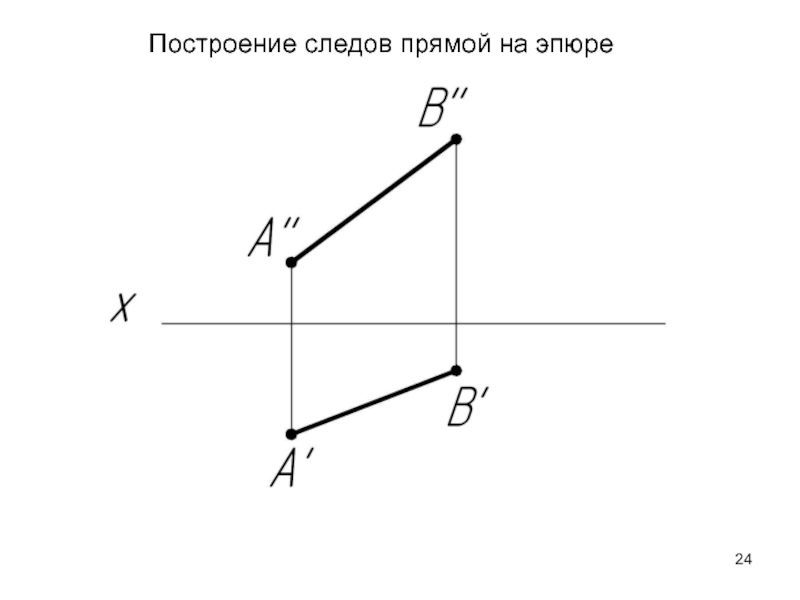
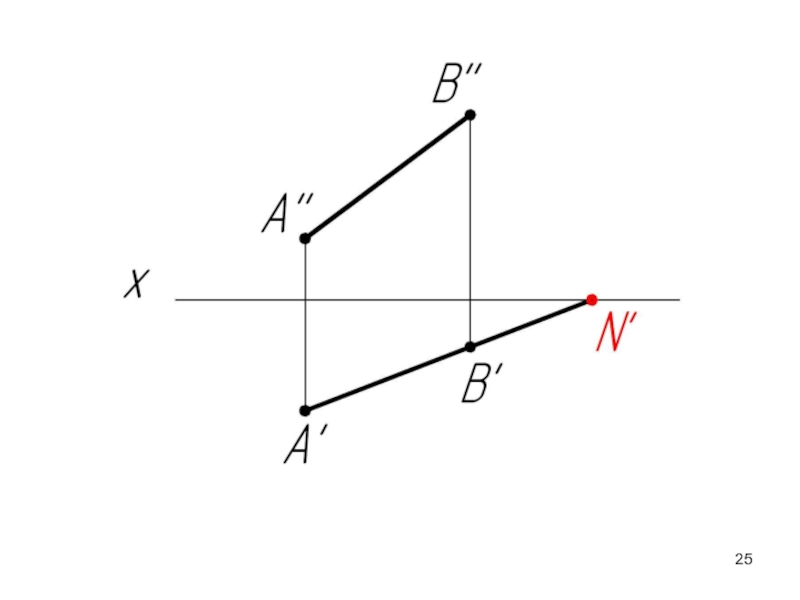
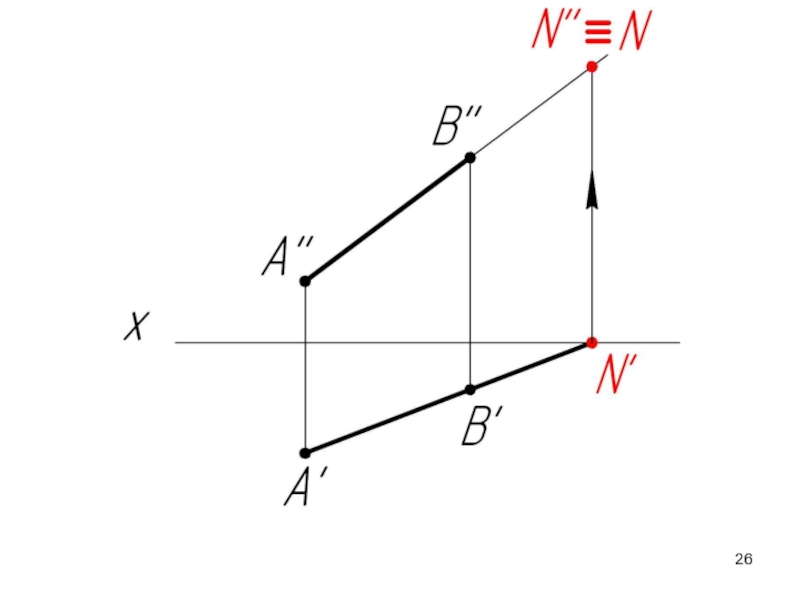
- 24. Построение следов прямой на эпюре
- 30. 2.3. Положение прямой относительно плоскостей проекций.
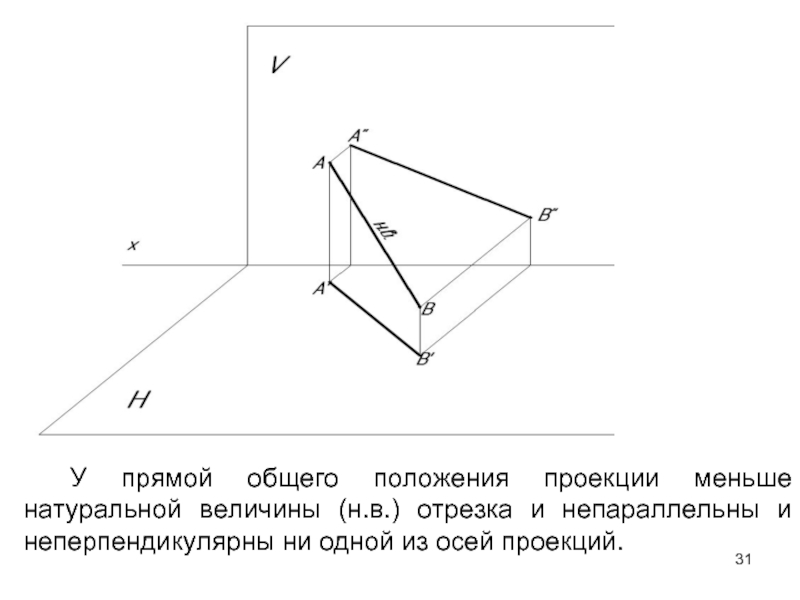
- 31. У прямой общего положения проекции меньше натуральной
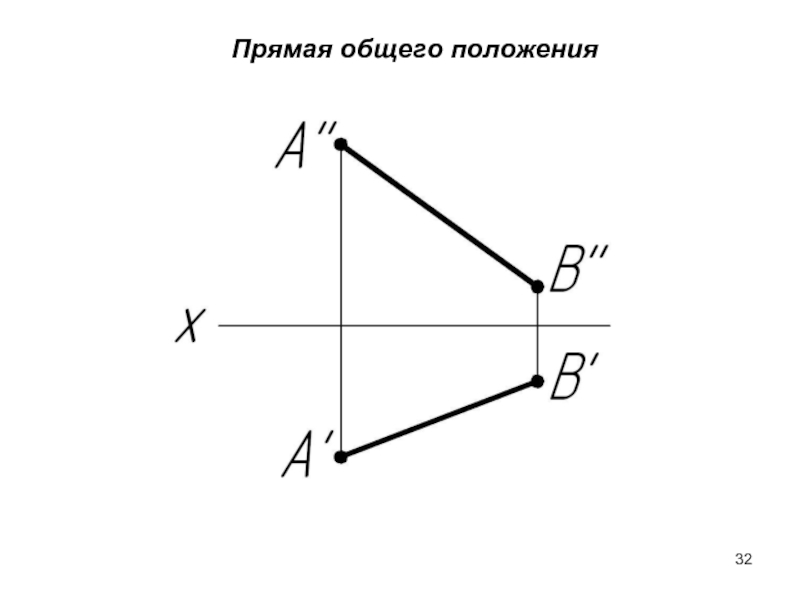
- 32. Прямая общего положения
- 33. Прямые уровня – прямые, параллельные одной из
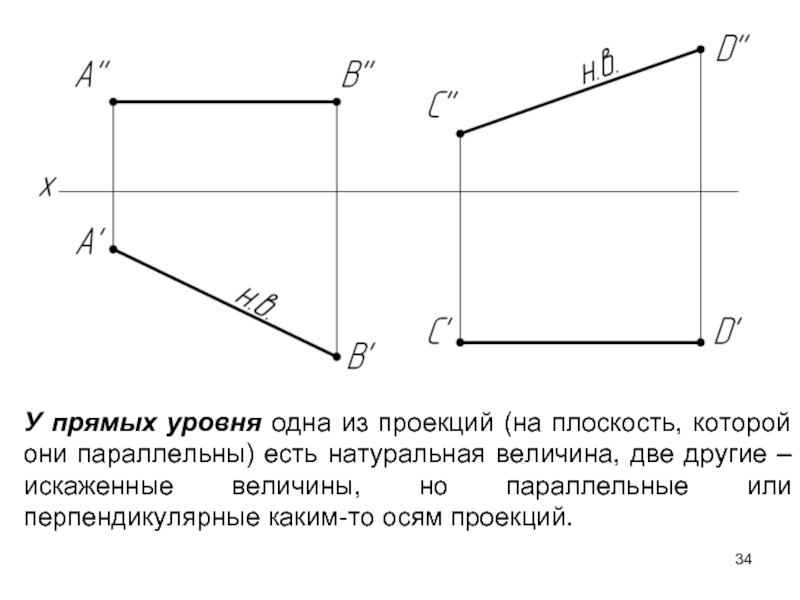
- 34. У прямых уровня одна из проекций (на
- 35. AB // H –
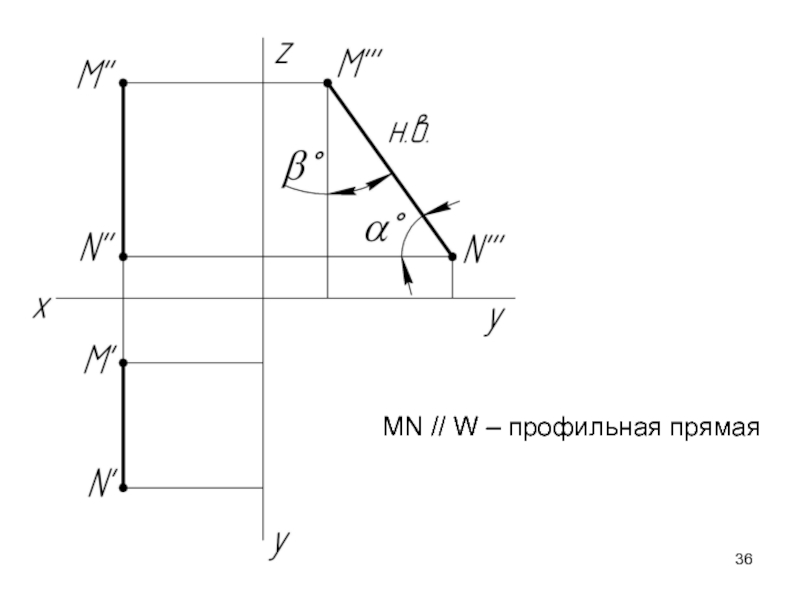
- 36. MN // W – профильная прямая
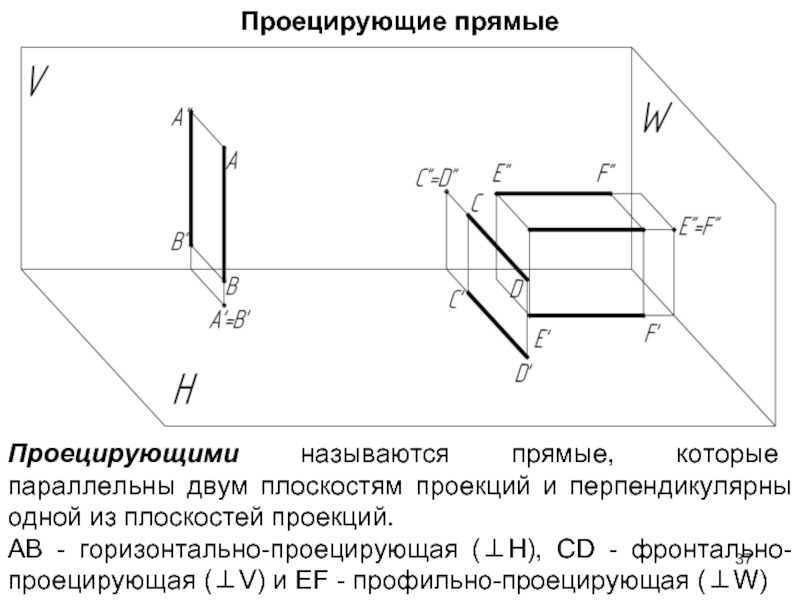
- 37. Проецирующие прямые Проецирующими называются прямые, которые параллельны
- 38. AB – горизонтально-проецирующая (AB⊥H) СD – фронтально-проецирующая
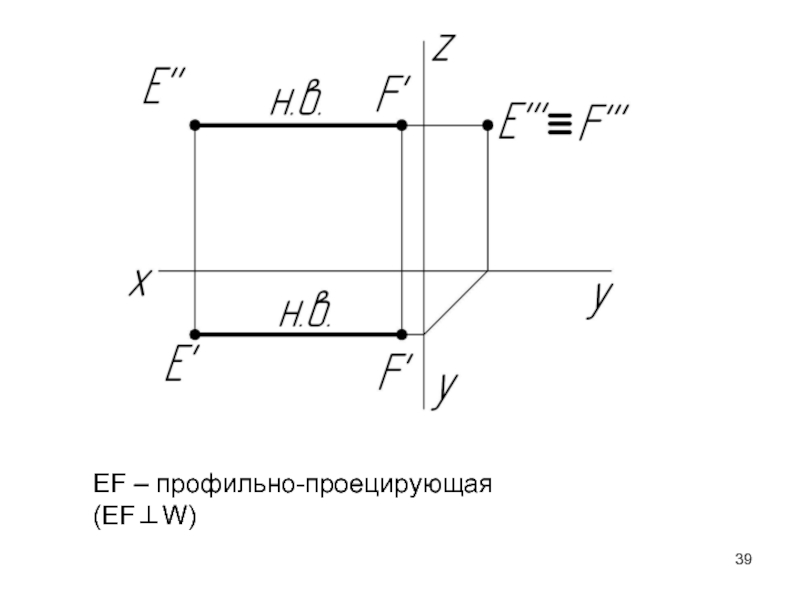
- 39. EF – профильно-проецирующая (EF⊥W)
- 40. 2.4. Относительное положение двух прямых По
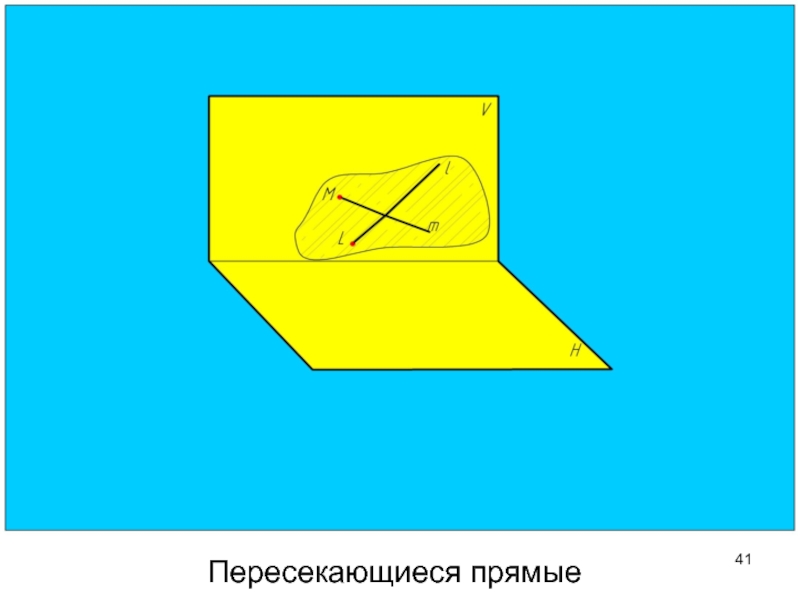
- 41. Пересекающиеся прямые
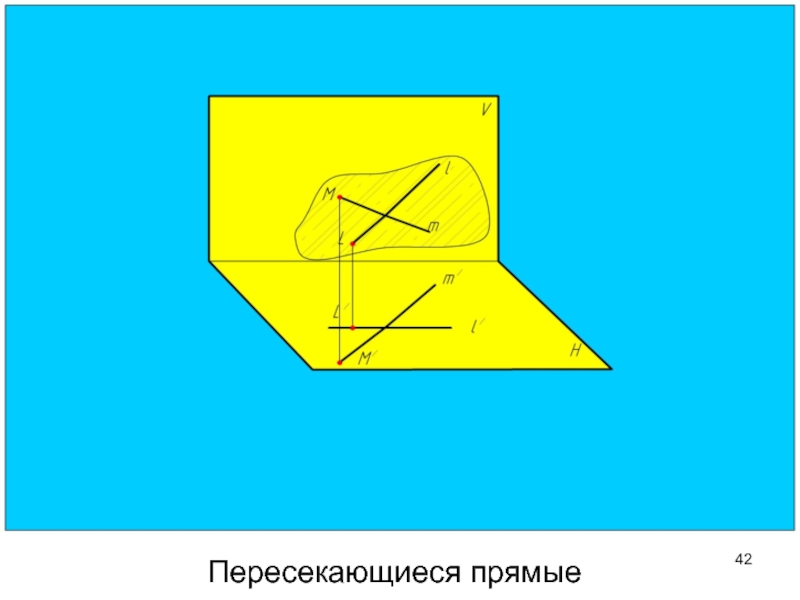
- 42. Пересекающиеся прямые
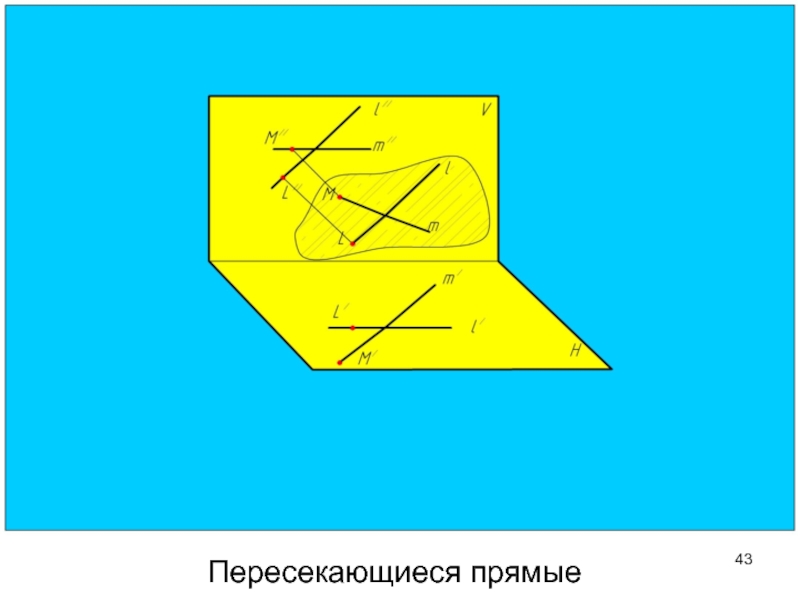
- 43. Пересекающиеся прямые
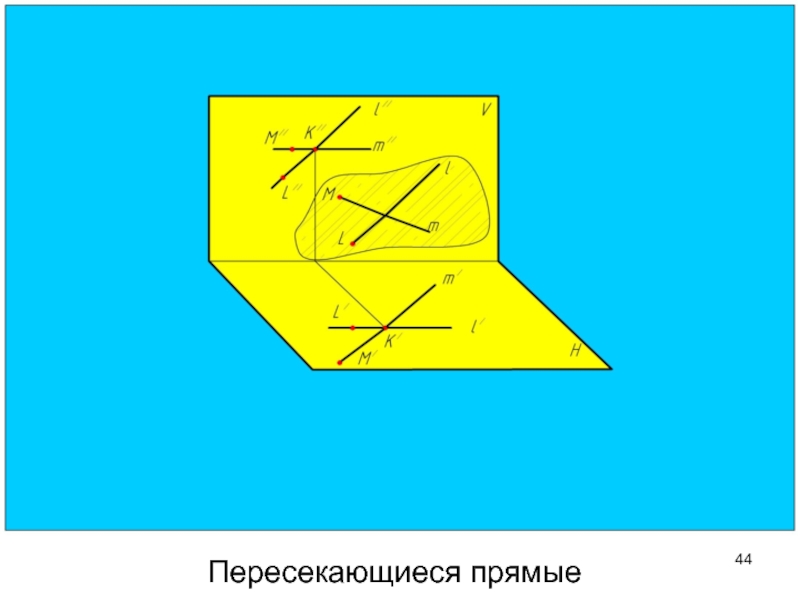
- 44. Пересекающиеся прямые
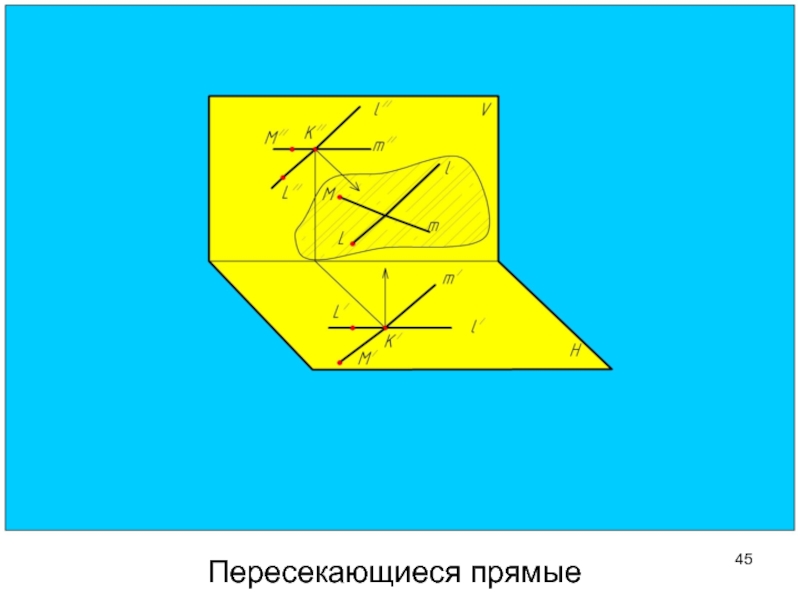
- 45. Пересекающиеся прямые
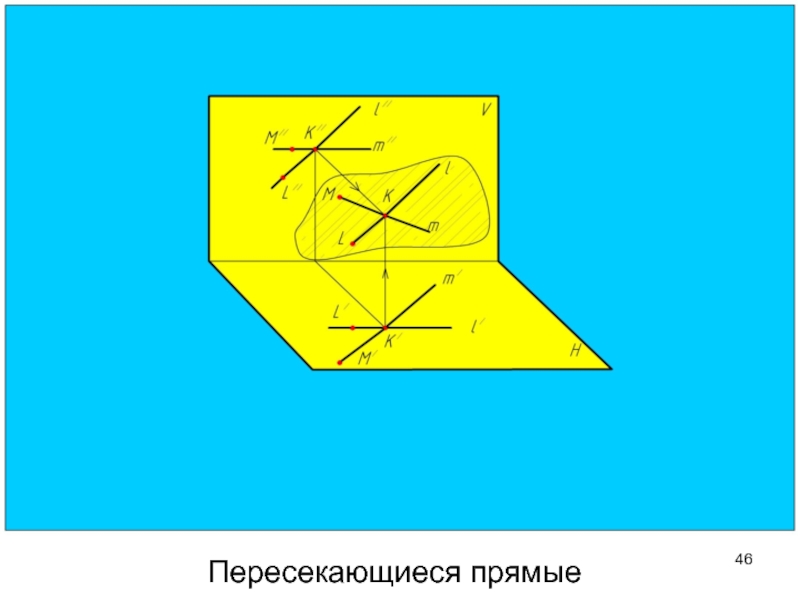
- 46. Пересекающиеся прямые
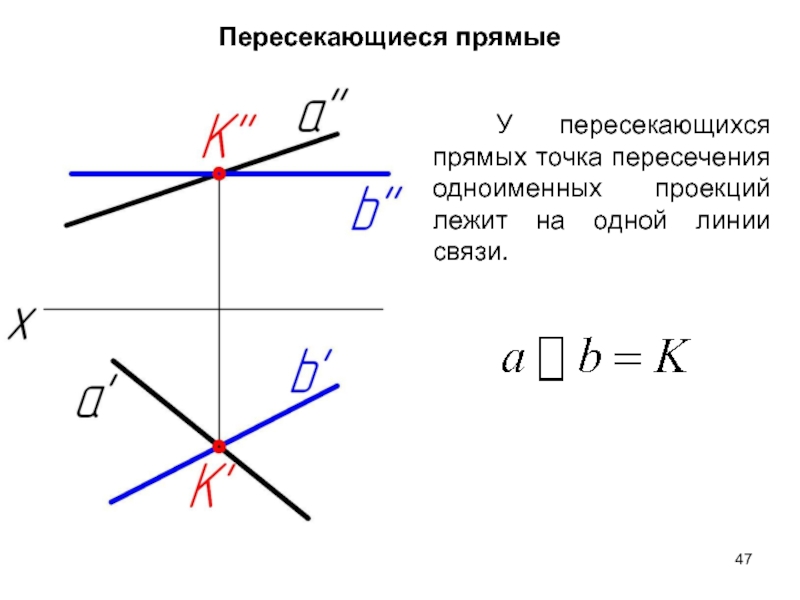
- 47. У пересекающихся прямых точка пересечения одноименных проекций
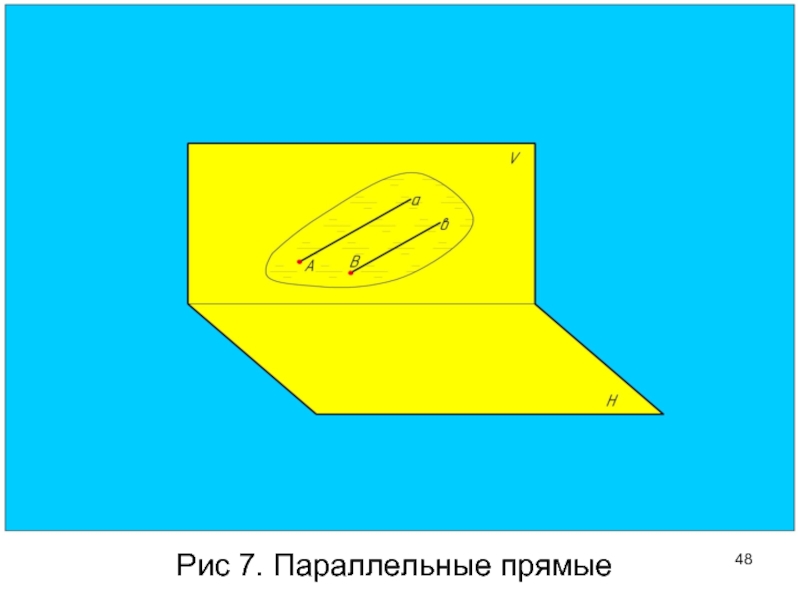
- 48. Рис 7. Параллельные прямые
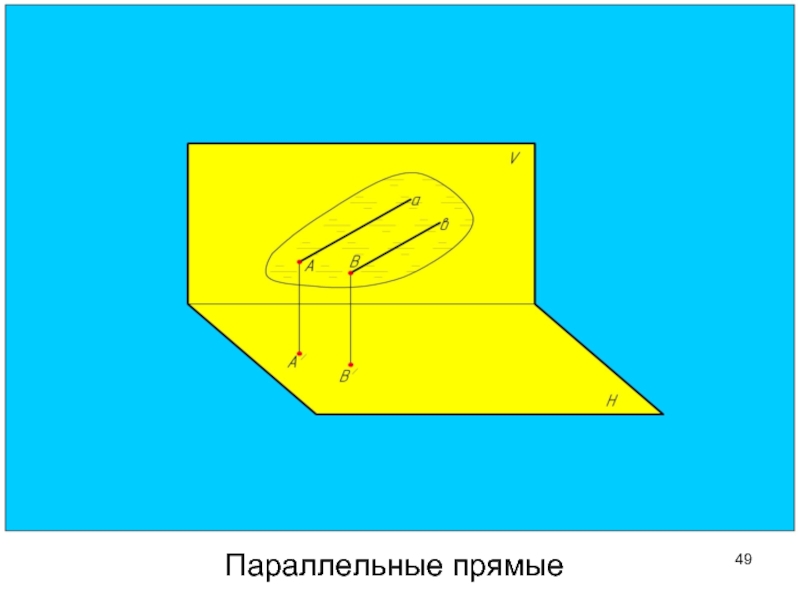
- 49. Параллельные прямые
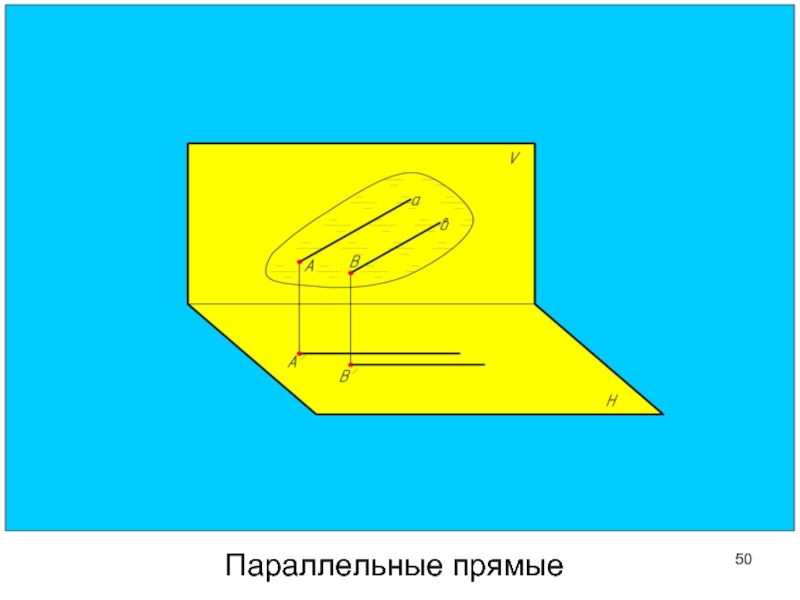
- 50. Параллельные прямые
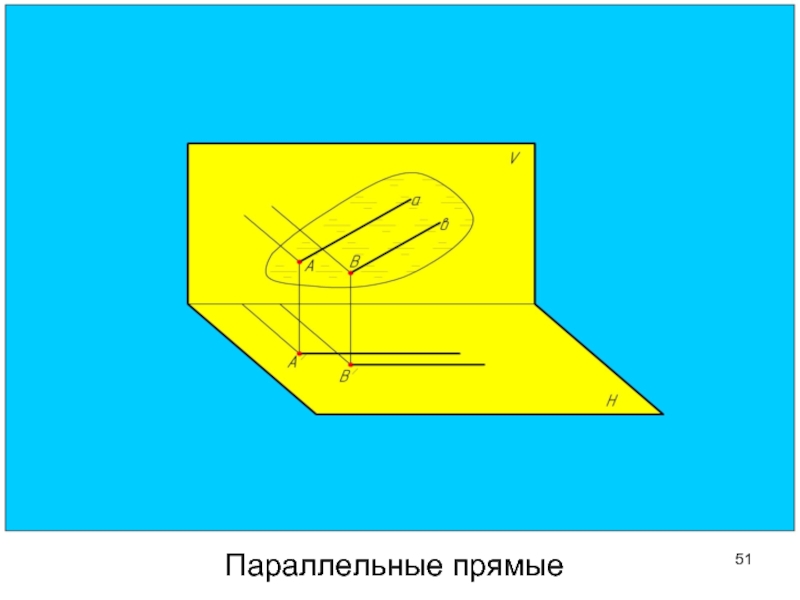
- 51. Параллельные прямые
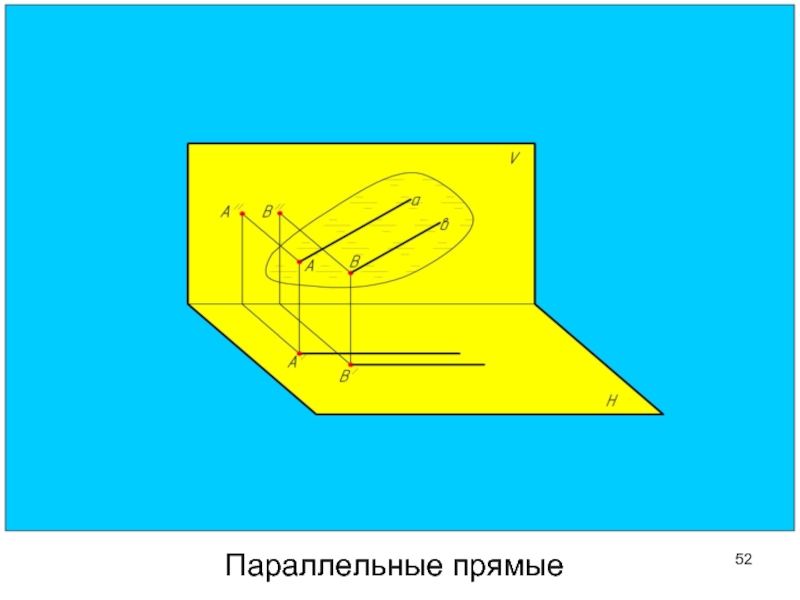
- 52. Параллельные прямые
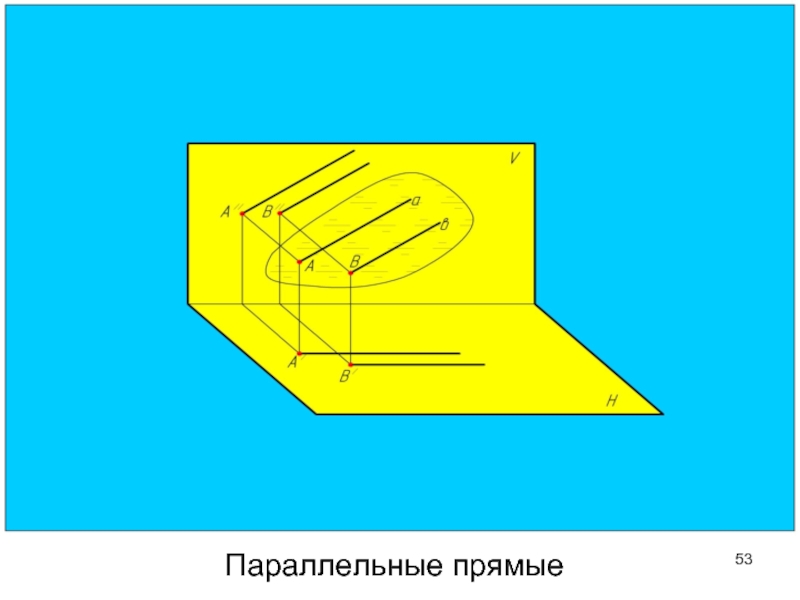
- 53. Параллельные прямые
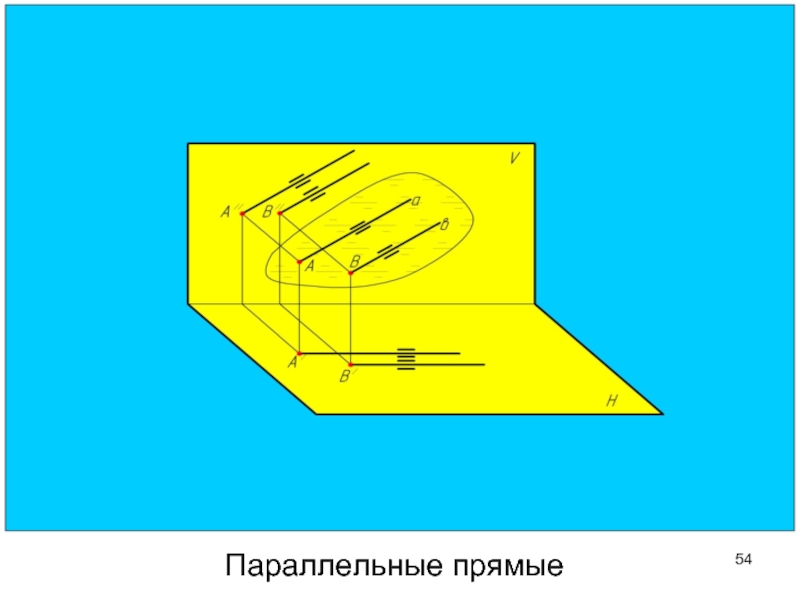
- 54. Параллельные прямые
- 55. У параллельных прямых одноименные проекции параллельны друг
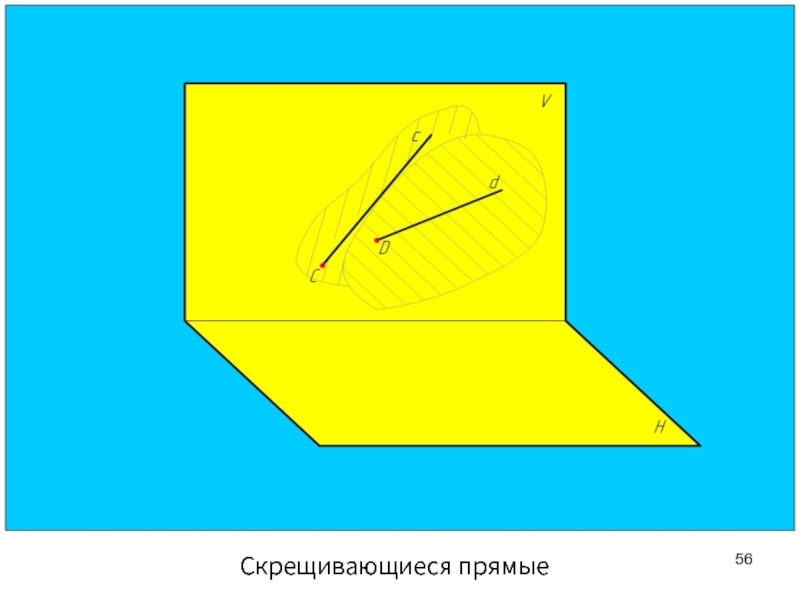
- 56. Скрещивающиеся прямые
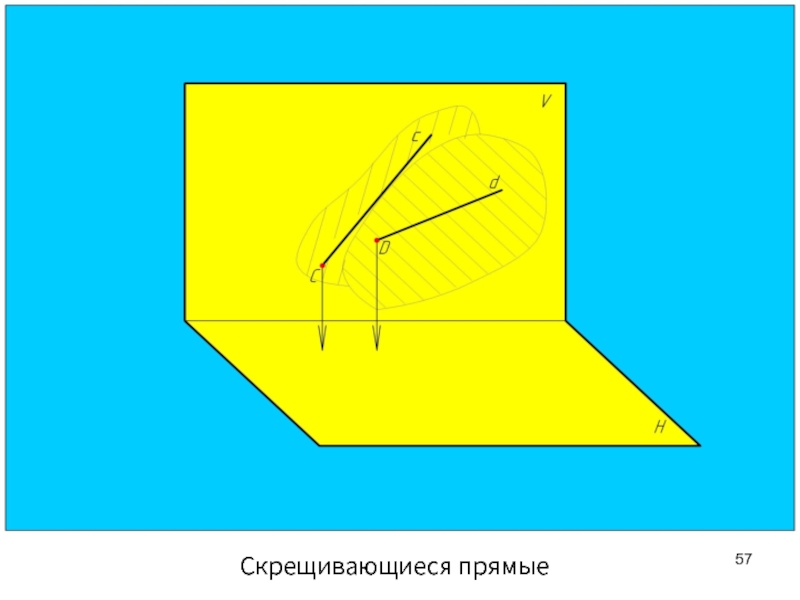
- 57. Скрещивающиеся прямые
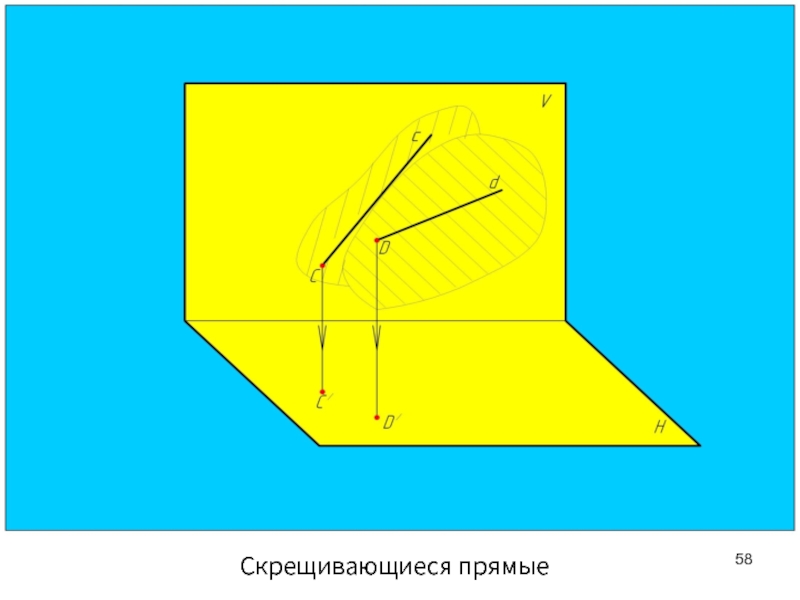
- 58. Скрещивающиеся прямые
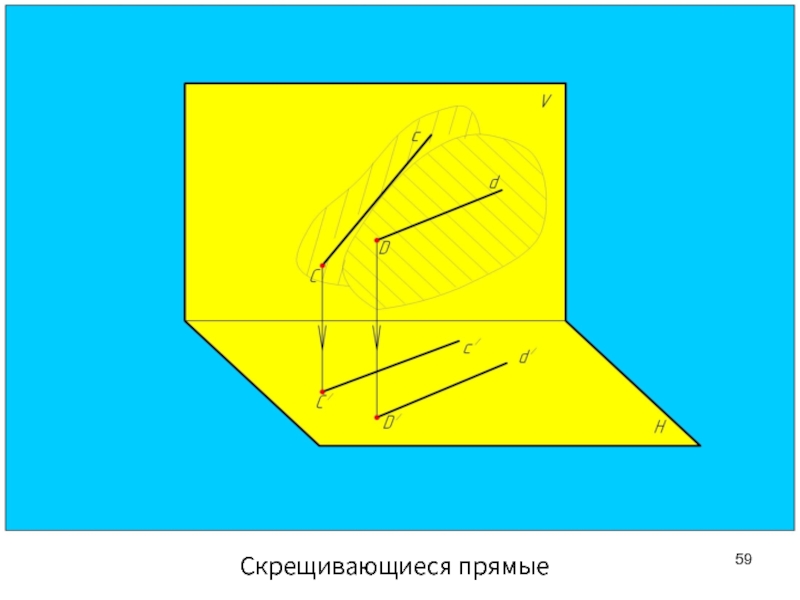
- 59. Скрещивающиеся прямые
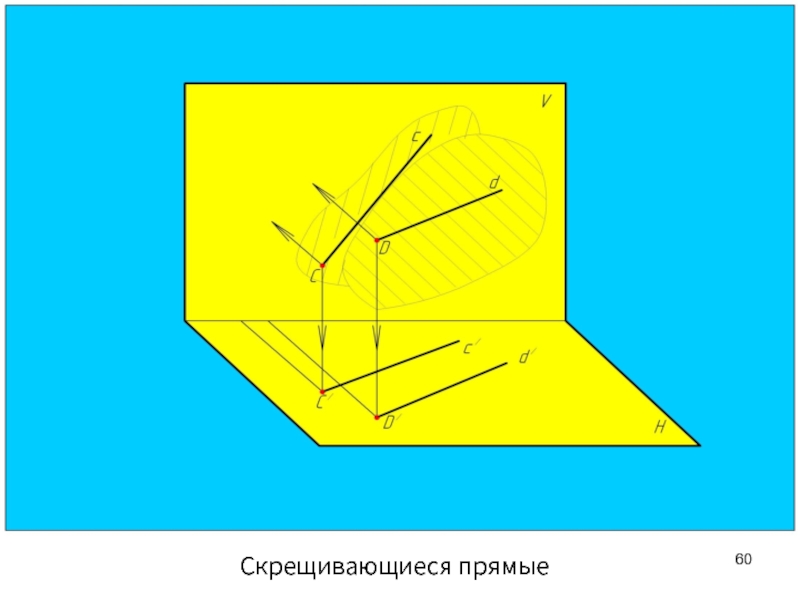
- 60. Скрещивающиеся прямые
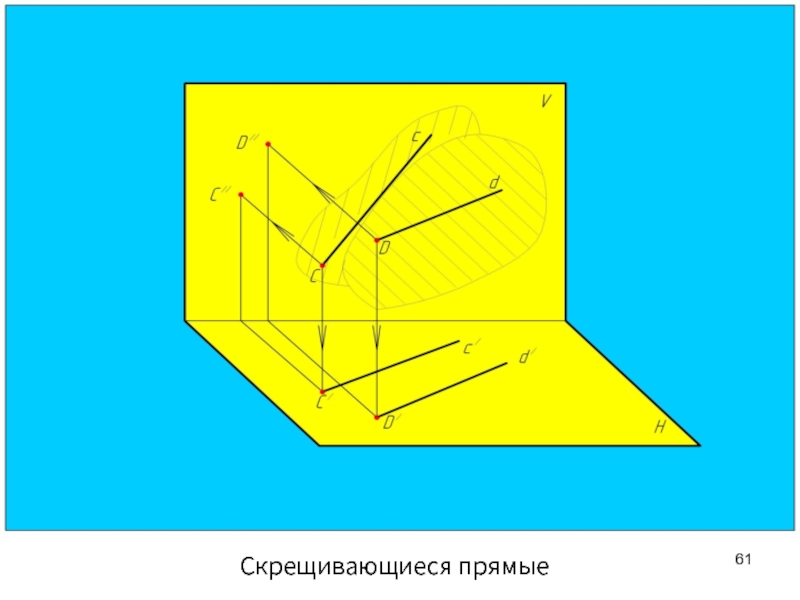
- 61. Скрещивающиеся прямые
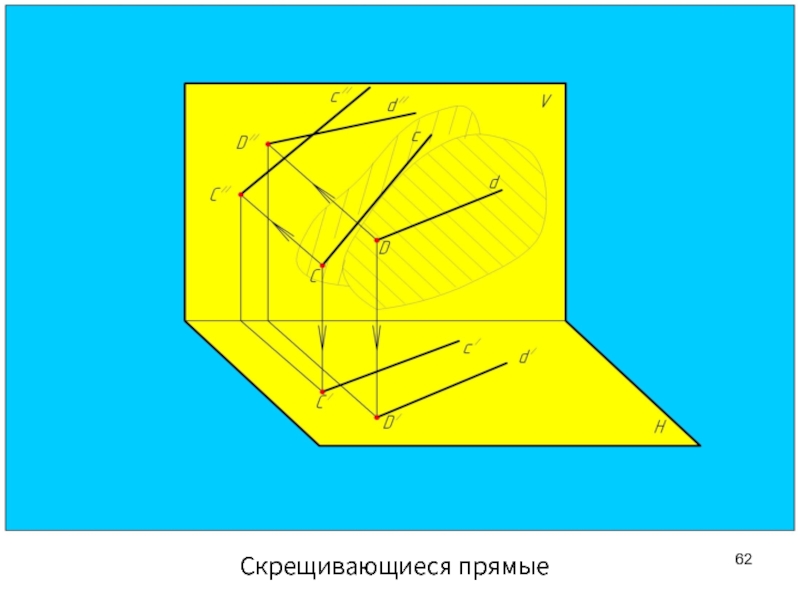
- 62. Скрещивающиеся прямые
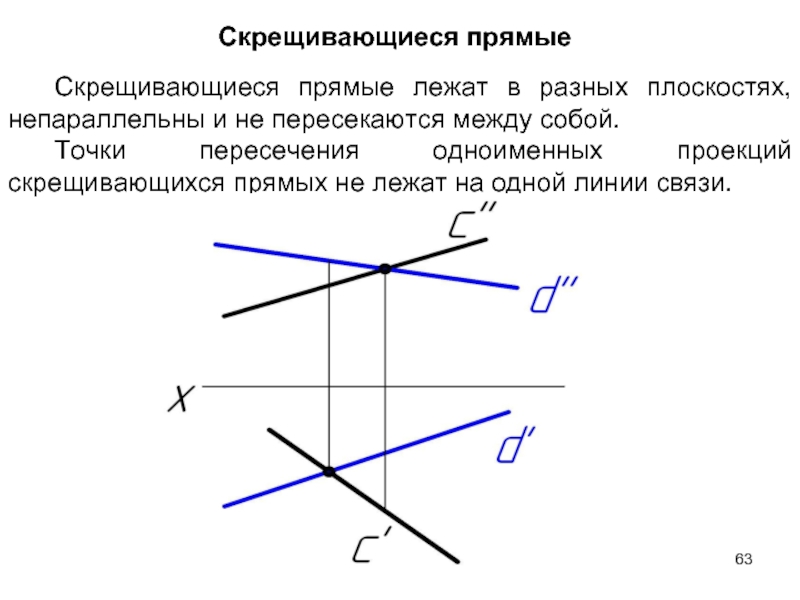
- 63. Скрещивающиеся прямые Скрещивающиеся прямые
- 64. Конкурирующие точки Точки, которые принадлежат разным прямым,
2.1. Проекции прямой. Принадлежность точки прямой. Проекция прямой линии – есть прямая.
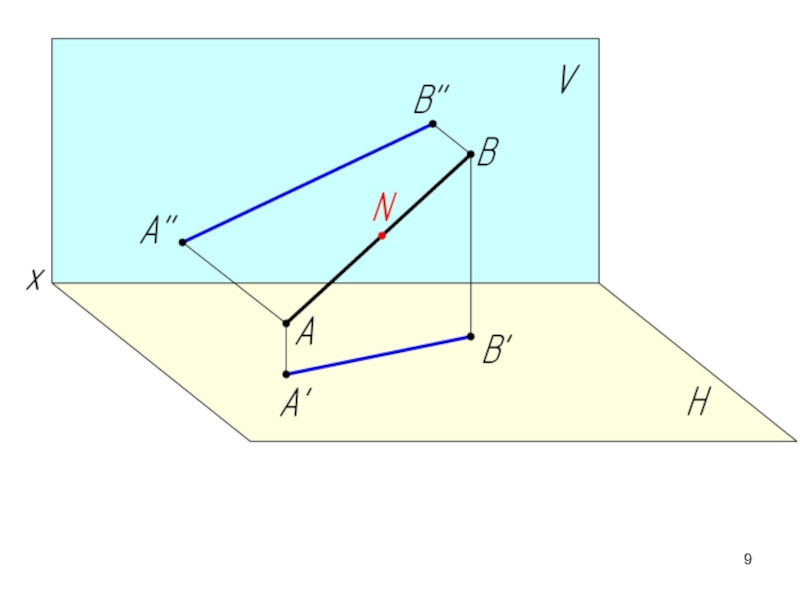
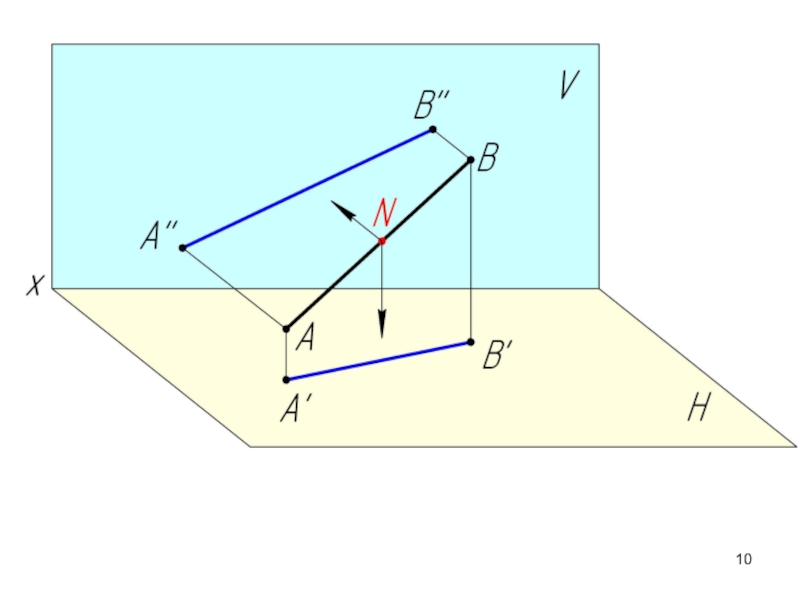
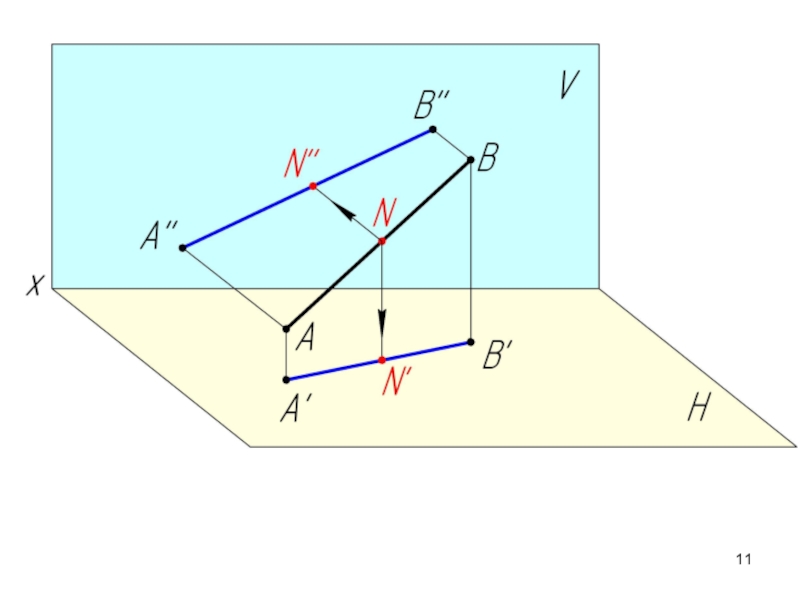
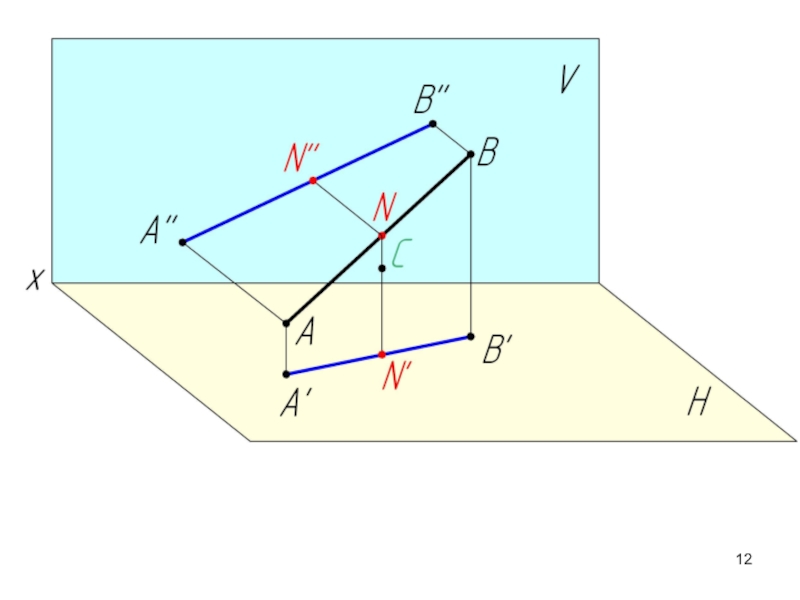
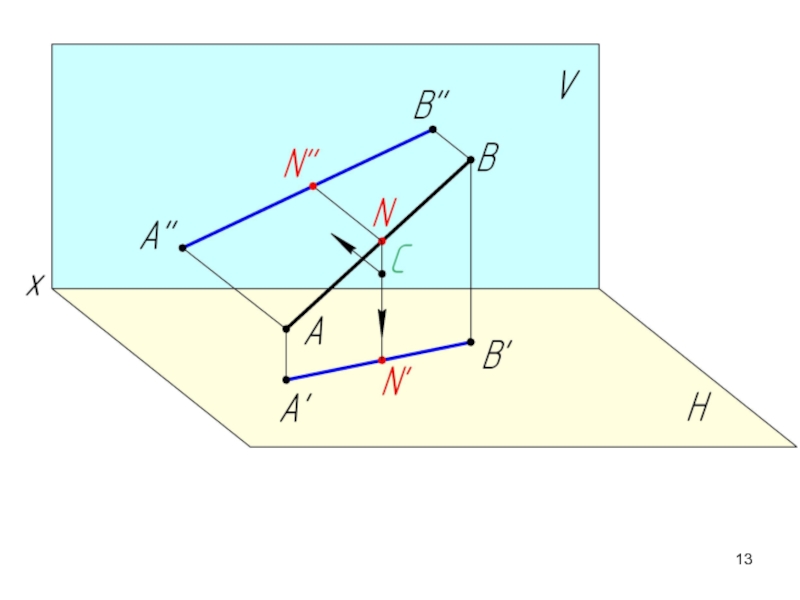
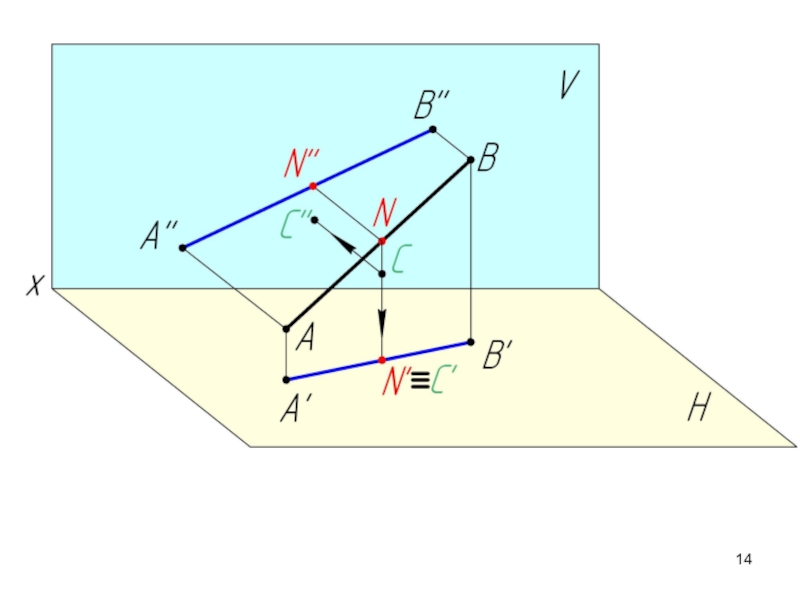
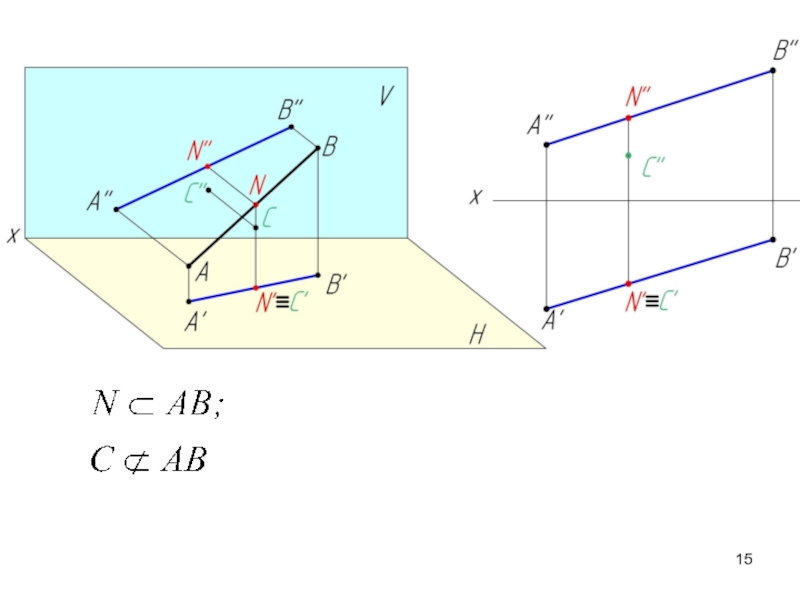
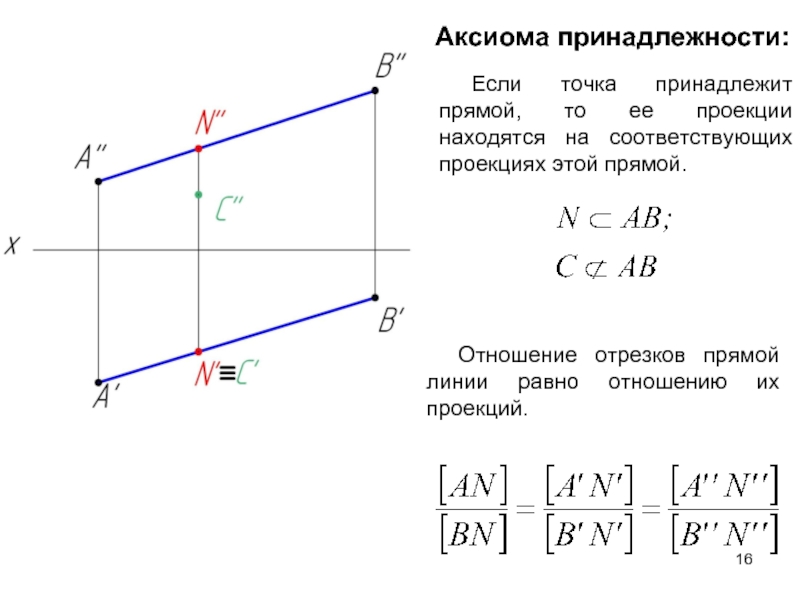
Слайд 16Если точка принадлежит прямой, то ее проекции находятся на соответствующих проекциях
этой прямой.
Аксиома принадлежности:
Отношение отрезков прямой линии равно отношению их проекций.
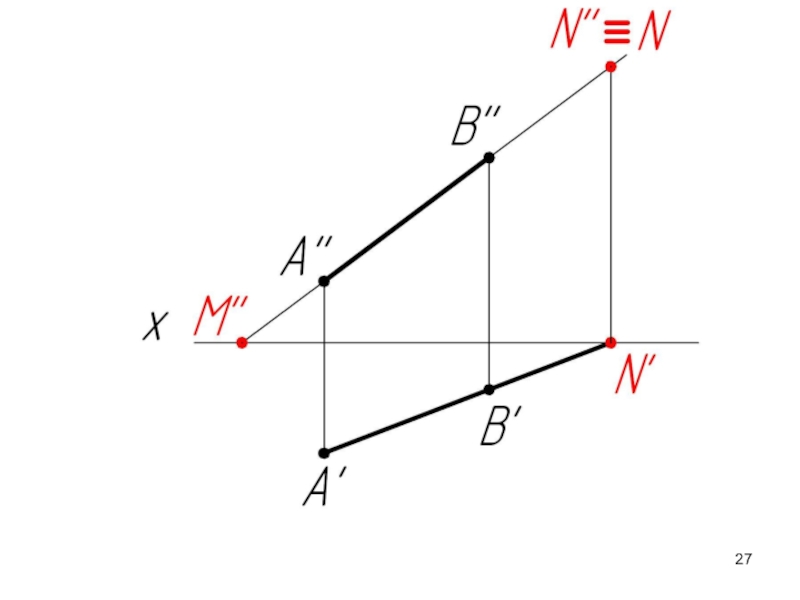
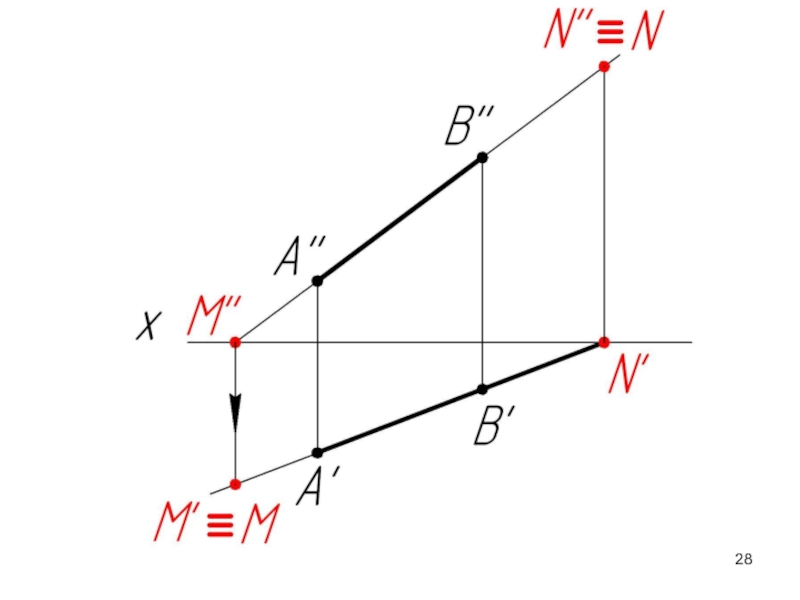
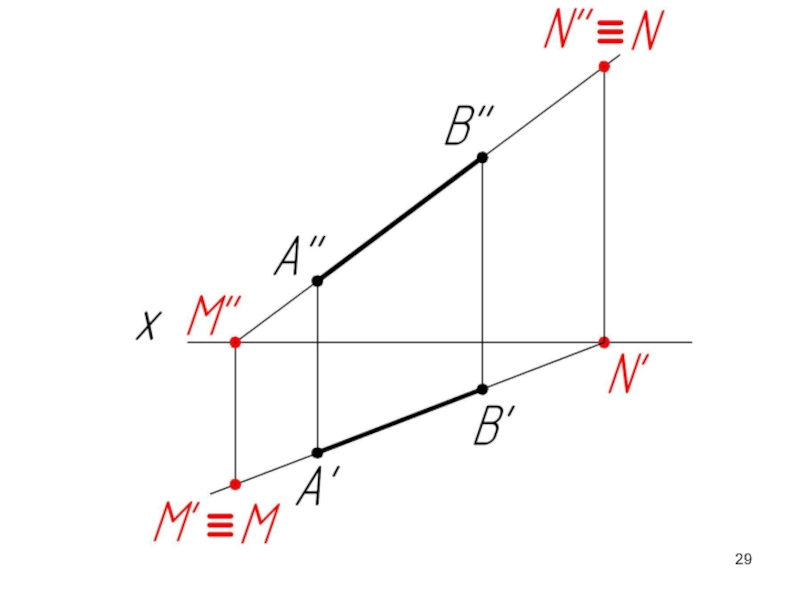
Слайд 23
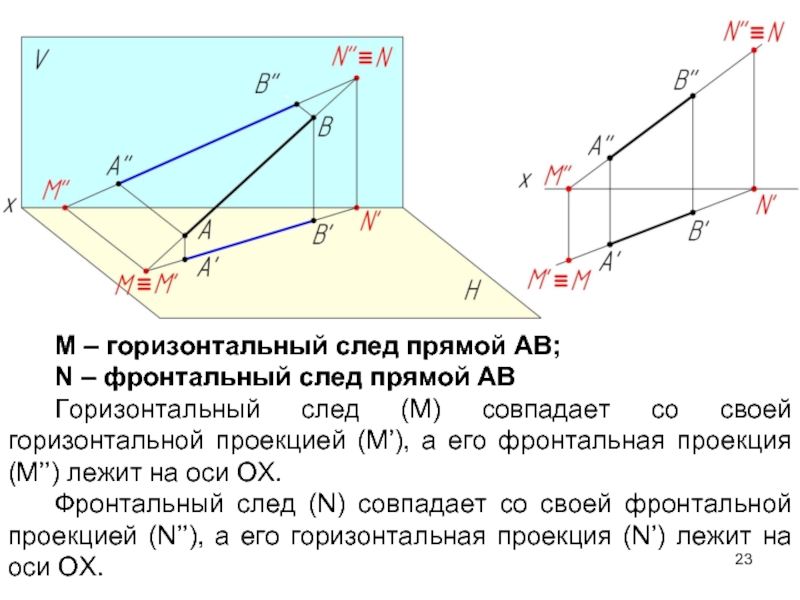
М – горизонтальный след прямой АВ;
N – фронтальный след прямой АВ
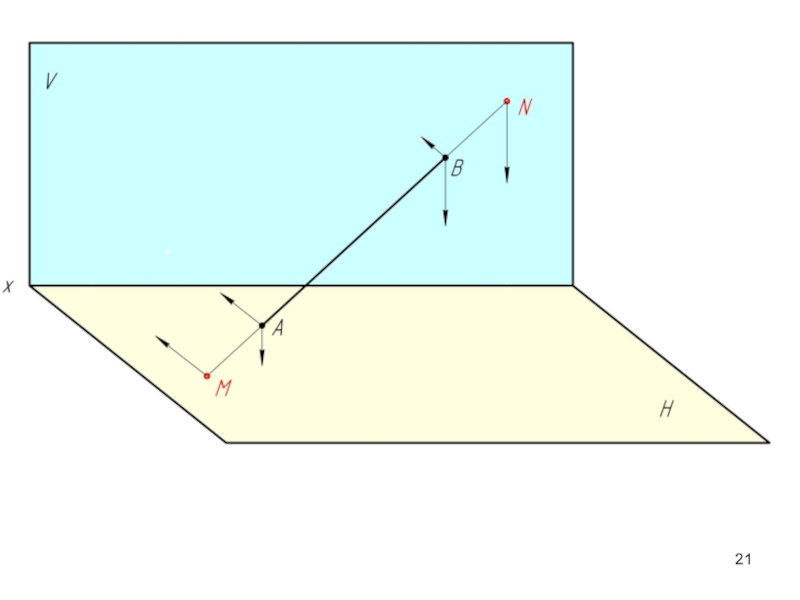
Горизонтальный
след (М) совпадает со своей горизонтальной проекцией (М’), а его фронтальная проекция (М’’) лежит на оси ОХ.
Фронтальный след (N) совпадает со своей фронтальной проекцией (N’’), а его горизонтальная проекция (N’) лежит на оси ОХ.
Фронтальный след (N) совпадает со своей фронтальной проекцией (N’’), а его горизонтальная проекция (N’) лежит на оси ОХ.
Слайд 302.3. Положение прямой относительно плоскостей проекций.
Прямая по отношению к плоскостям проекций
H, V, W может занимать следующие положения:
1 - общее положение
2 - частное положение:
- прямые уровня;
- проецирующие прямые.
Прямая общего положения – это прямая, которая не параллельна ни одной из плоскостей проекций.
1 - общее положение
2 - частное положение:
- прямые уровня;
- проецирующие прямые.
Прямая общего положения – это прямая, которая не параллельна ни одной из плоскостей проекций.
Слайд 31У прямой общего положения проекции меньше натуральной величины (н.в.) отрезка и
непараллельны и неперпендикулярны ни одной из осей проекций.
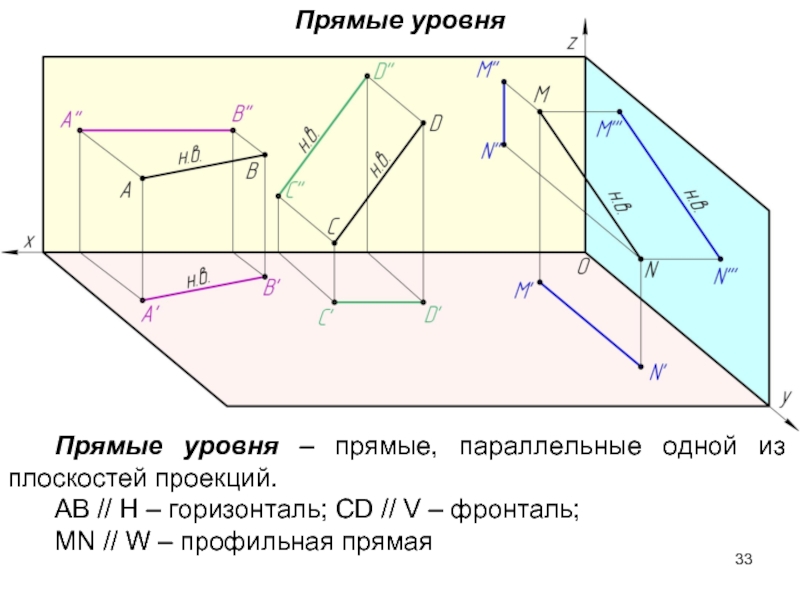
Слайд 33Прямые уровня – прямые, параллельные одной из плоскостей проекций.
AB // H
– горизонталь; CD // V – фронталь;
MN // W – профильная прямая
MN // W – профильная прямая
Прямые уровня
Слайд 34У прямых уровня одна из проекций (на плоскость, которой они параллельны)
есть натуральная величина, две другие – искаженные величины, но параллельные или перпендикулярные каким-то осям проекций.
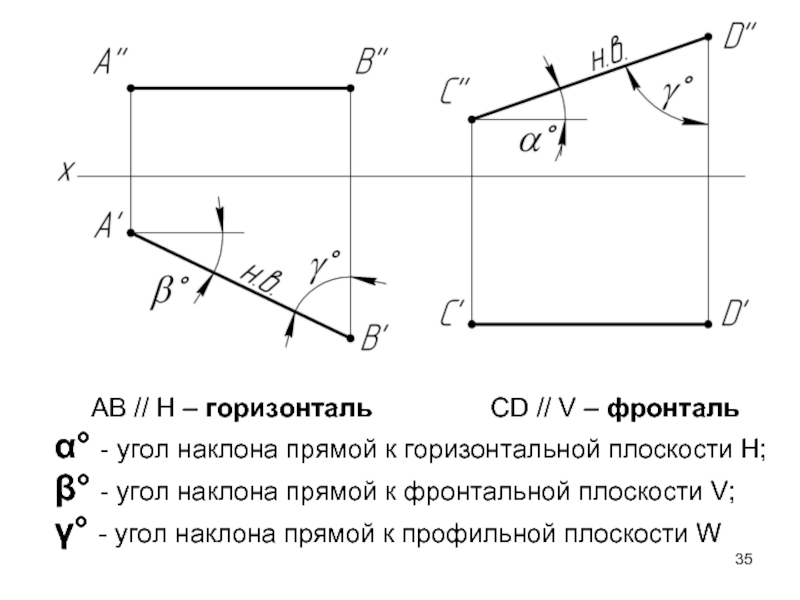
Слайд 35 AB // H – горизонталь
CD // V – фронталь
α° - угол наклона прямой к горизонтальной плоскости Н;
β° - угол наклона прямой к фронтальной плоскости V;
γ° - угол наклона прямой к профильной плоскости W
α° - угол наклона прямой к горизонтальной плоскости Н;
β° - угол наклона прямой к фронтальной плоскости V;
γ° - угол наклона прямой к профильной плоскости W
Слайд 37Проецирующие прямые
Проецирующими называются прямые, которые параллельны двум плоскостям проекций и перпендикулярны
одной из плоскостей проекций.
АВ - горизонтально-проецирующая (⊥H), CD - фронтально-проецирующая (⊥V) и EF - профильно-проецирующая (⊥W)
АВ - горизонтально-проецирующая (⊥H), CD - фронтально-проецирующая (⊥V) и EF - профильно-проецирующая (⊥W)
Слайд 38AB – горизонтально-проецирующая (AB⊥H)
СD – фронтально-проецирующая (CD⊥V)
У проецирующих прямых одна из
проекций (на плоскость, которой они перпендикулярны) есть точка, две другие – натуральные величины, но параллельные или перпендикулярные каким-то осям проекций.
Слайд 402.4. Относительное положение двух прямых
По своему взаимному положению две прямые могут
быть:
пересекающимися
параллельными
скрещивающимися.
пересекающимися
параллельными
скрещивающимися.
Слайд 47У пересекающихся прямых точка пересечения одноименных проекций лежит на одной линии
связи.
Пересекающиеся прямые
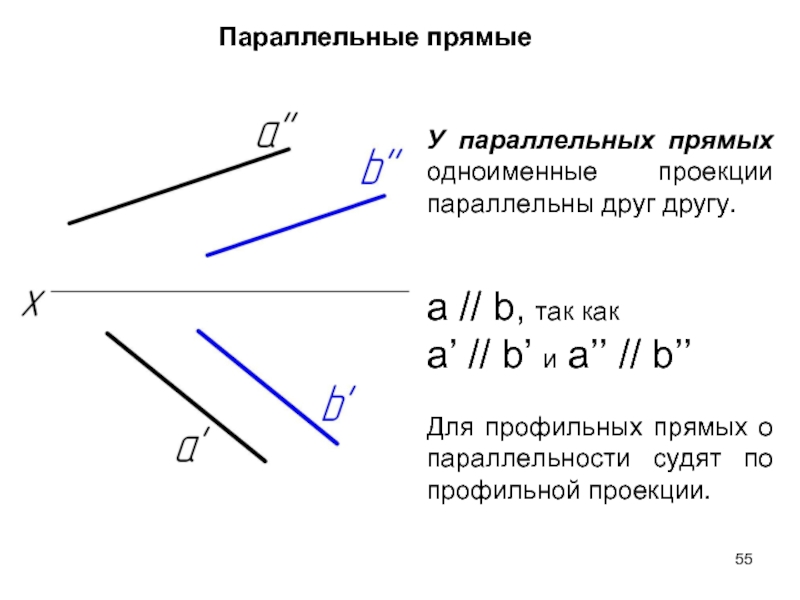
Слайд 55У параллельных прямых одноименные проекции параллельны друг другу.
a // b, так
как
а’ // b’ и a’’ // b’’
Для профильных прямых о параллельности судят по профильной проекции.
а’ // b’ и a’’ // b’’
Для профильных прямых о параллельности судят по профильной проекции.
Параллельные прямые
Слайд 63
Скрещивающиеся прямые
Скрещивающиеся прямые лежат в разных плоскостях, непараллельны и не
пересекаются между собой.
Точки пересечения одноименных проекций скрещивающихся прямых не лежат на одной линии связи.
Точки пересечения одноименных проекций скрещивающихся прямых не лежат на одной линии связи.
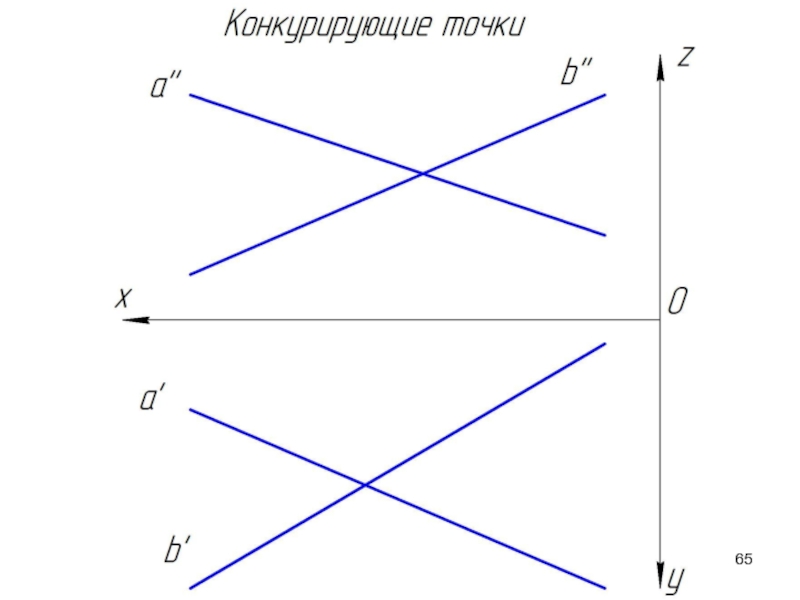
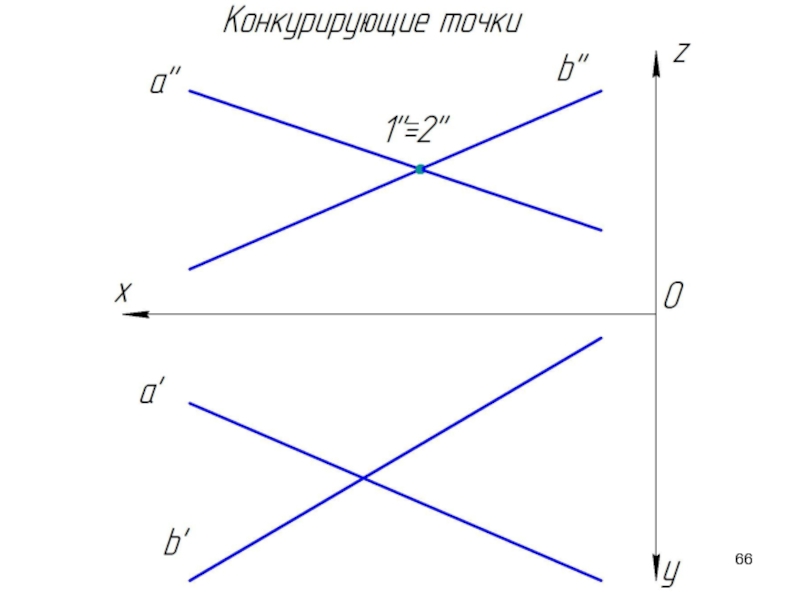
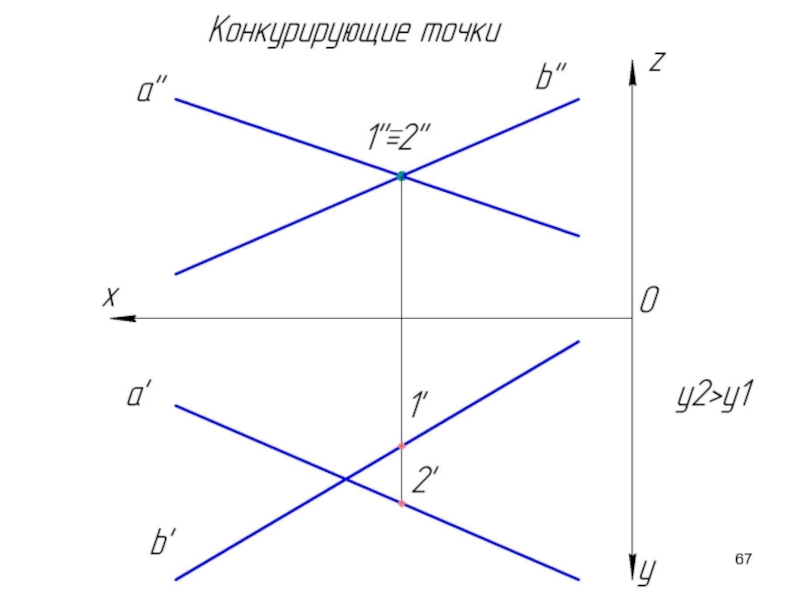
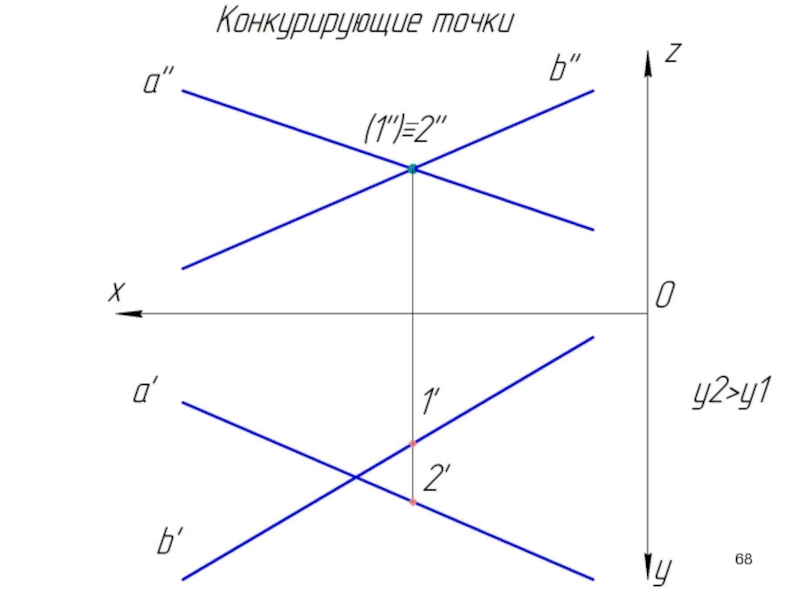
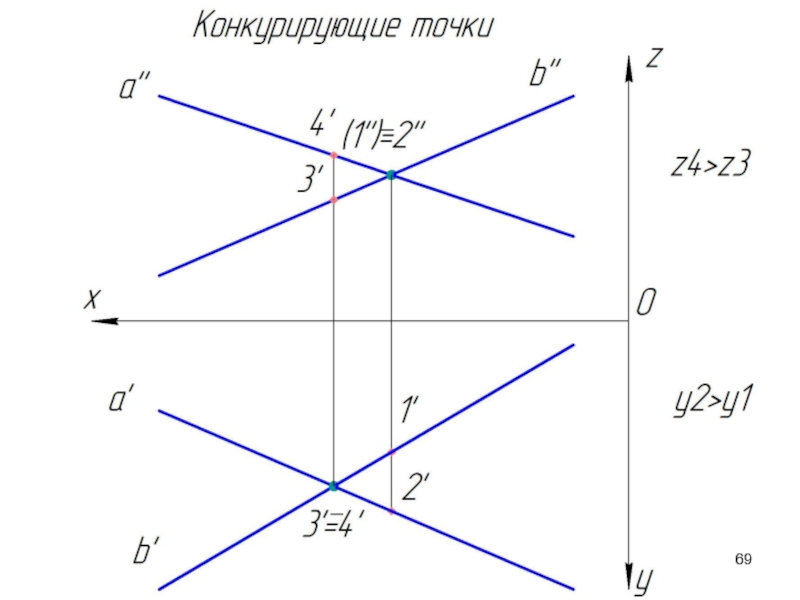
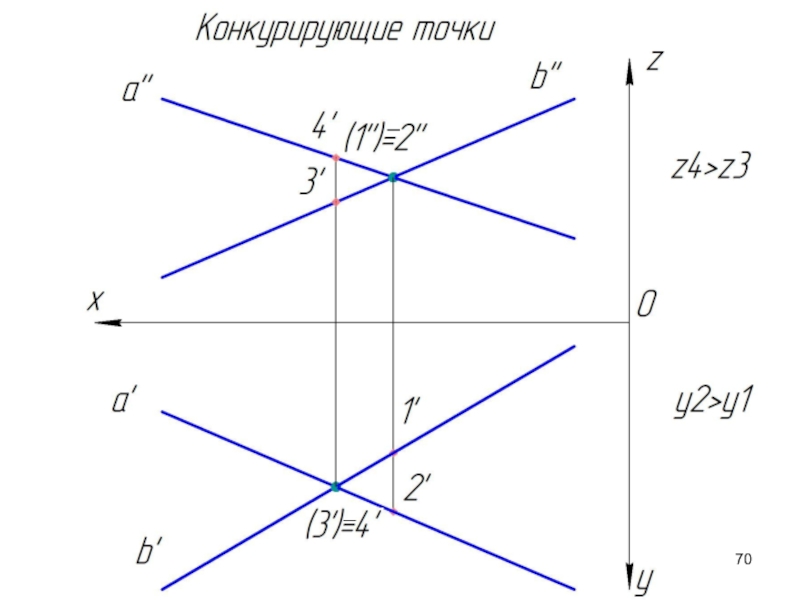
Слайд 64Конкурирующие точки
Точки, которые принадлежат разным прямым, но проекции которых совпадают, называются
конкурирующими.
С помощью конкурирующих точек определяется взаимная видимость геометрических образов. Пусть заданы две скрещивающихся прямые a и b. Определим какая проекция какой прямой накладывается на другую.
С помощью конкурирующих точек определяется взаимная видимость геометрических образов. Пусть заданы две скрещивающихся прямые a и b. Определим какая проекция какой прямой накладывается на другую.
