- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Проецирование. Виды проецирования презентация
Содержание
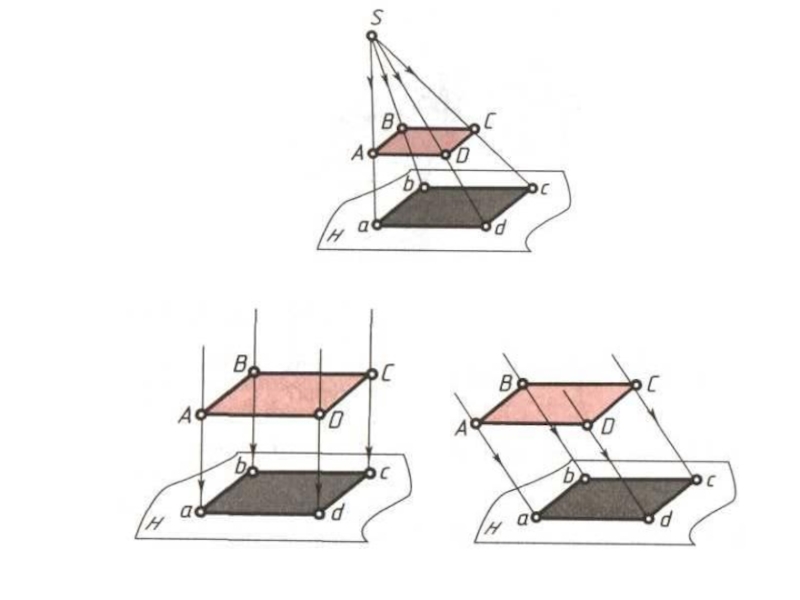
- 1. Проецирование. Виды проецирования
- 2. Виды проецирования
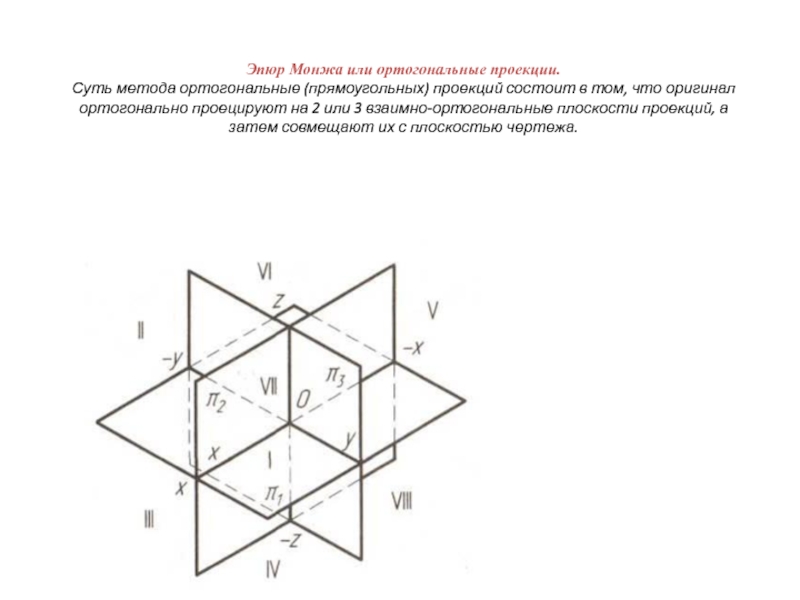
- 4. Эпюр Монжа или ортогональные проекции. Суть
- 5. Проекции точки, линии, плоскости
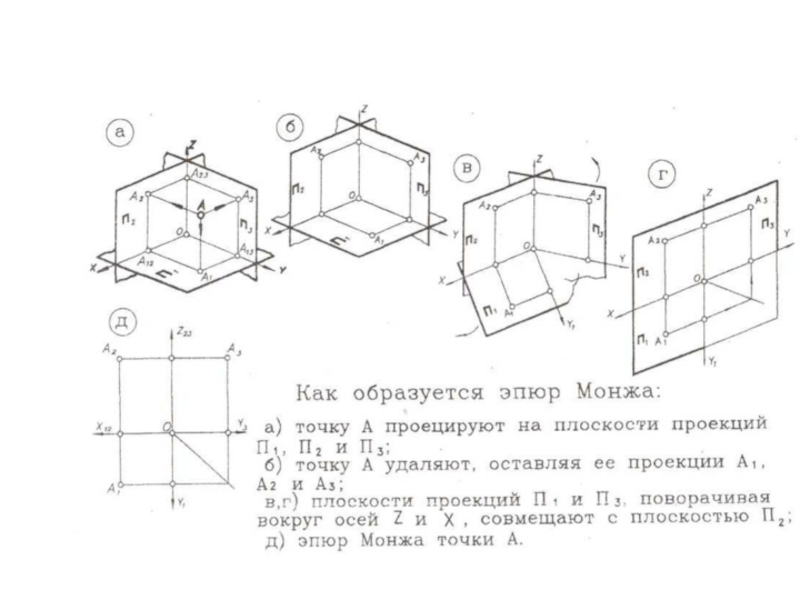
- 7. Полученный
- 9. Так как две точки
- 10. Комплексный чертеж прямой общего положения
- 11. Прямая частного положения
- 17. Взаимное положение прямых: параллельные линии, пересекающиеся линии, скрещивающиеся линии
- 18. взаимное положение точки и прямой
- 19. х
- 20. х
- 21. Плоскость относительно плоскостей проекций
- 22. Плоскости, параллельные плоскостям проекций называются плоскостями уровня Горизонтальная плоскость
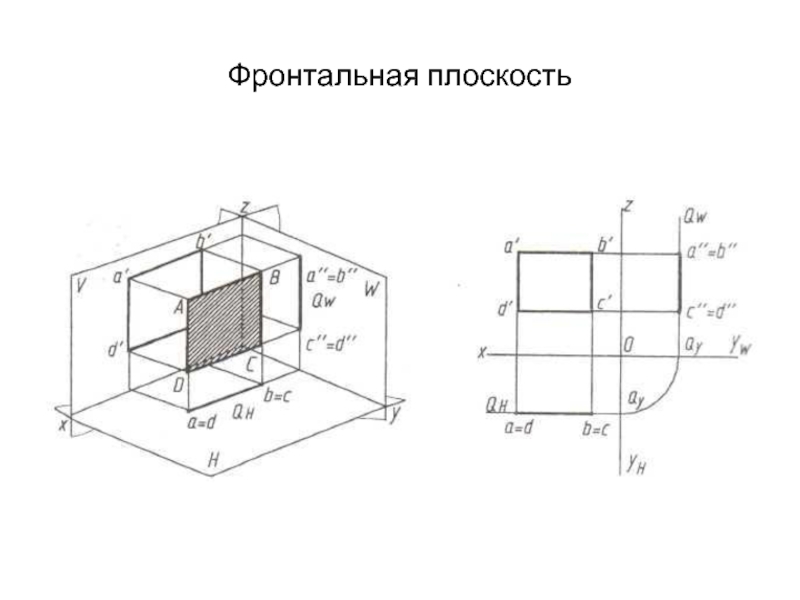
- 23. Фронтальная плоскость
- 24. Профильная плоскость
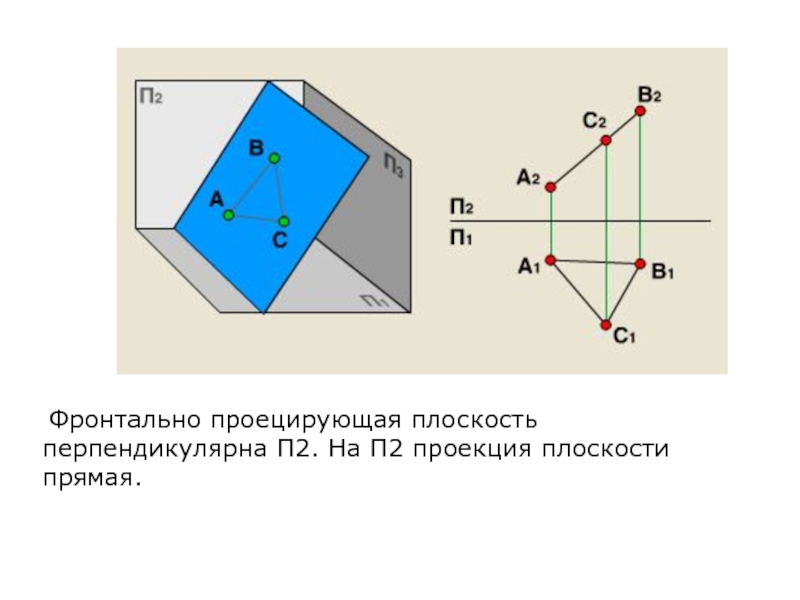
- 25. Фронтально
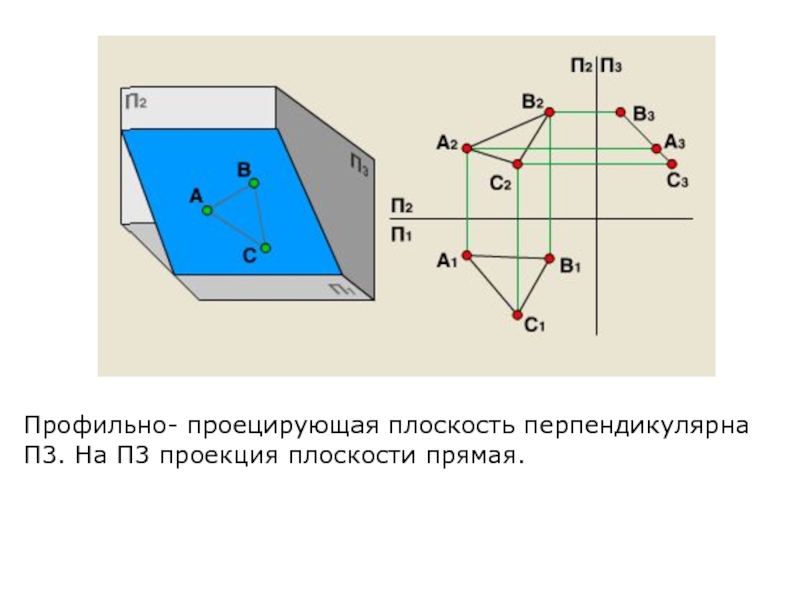
- 26. Профильно- проецирующая плоскость перпендикулярна П3. На П3 проекция плоскости прямая.
- 27. х А2 В2
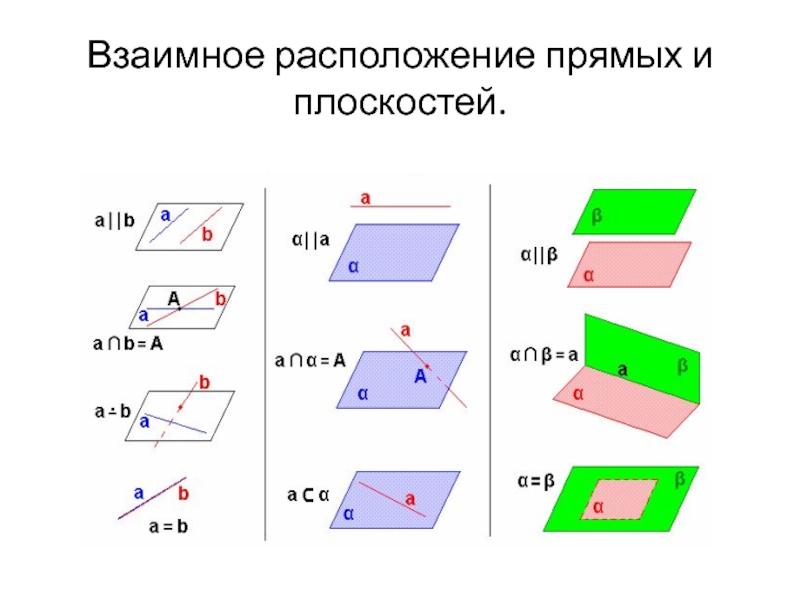
- 28. Взаимное расположение прямых и плоскостей.
- 29. Проекции объемных тел
- 31. Ортогональная проекции куба
- 32. Ортогональная проекции шестиугольной призмы
- 33. Ортогональная проекции цилиндра
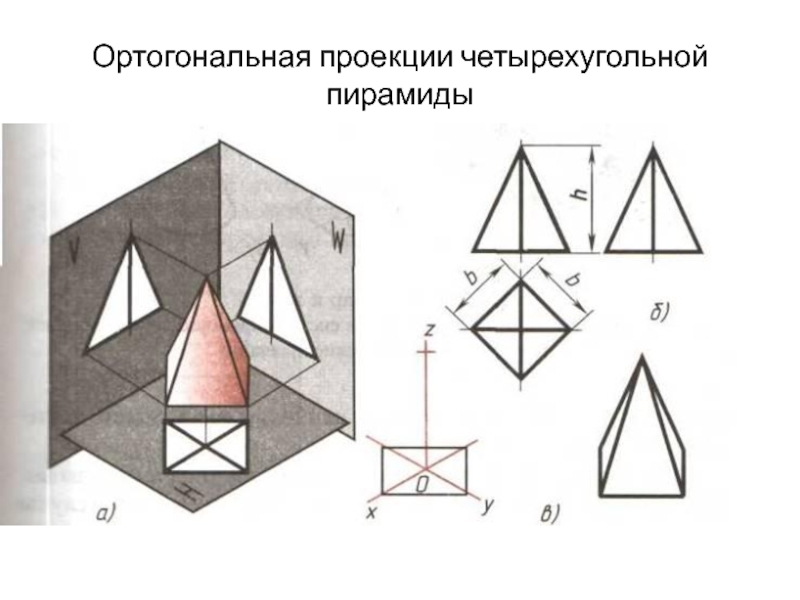
- 34. Ортогональная проекции четырехугольной пирамиды
- 35. Построение третьей проекции шестиугольной призмы
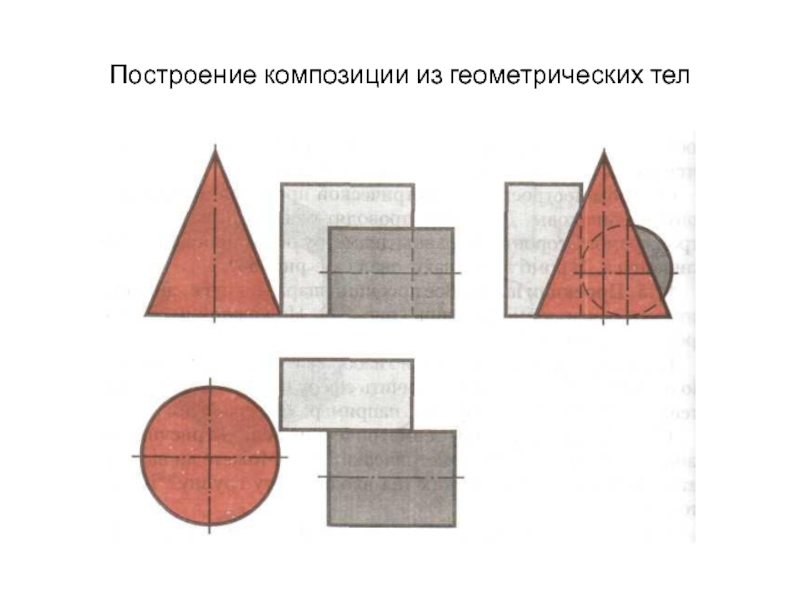
- 36. Построение композиции из геометрических тел
Слайд 4 Эпюр Монжа или ортогональные проекции. Суть метода ортогональные (прямоугольных) проекций состоит в
Слайд 7
Полученный чертеж является трёхпроекционным ортогональным чертежом точки
На чертеже линии связи А2 А1 и А2 А3 перпендикулярны к соответствующим осям. По ортогональному чертежу можно судить о расстоянии от точки А до плоскостей П1, П2 и П3.
Слайд 8
α
β
A1
B1
A
A2
Ax
B
B2
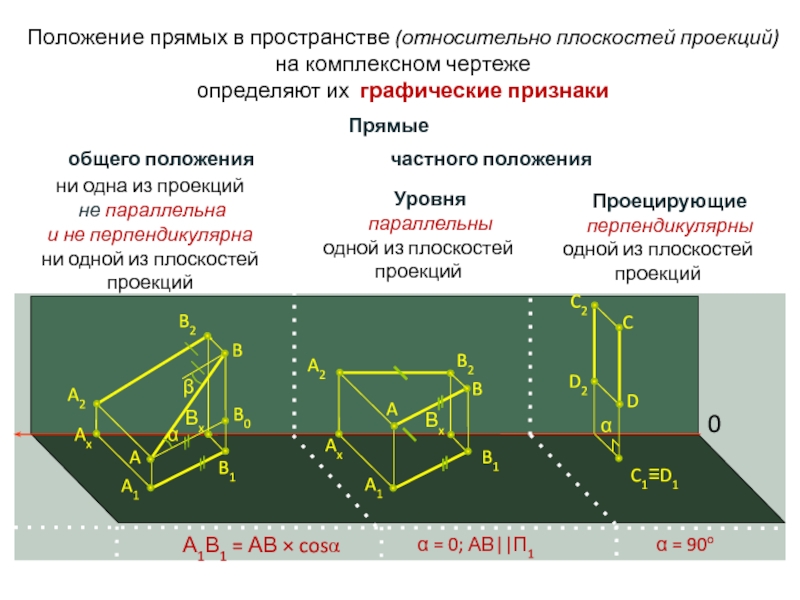
α = 0; АВ||П1
A1
B1
A
A2
Ax
C
C2
0
B
B2
D
D2
C1≡D1
α = 90o
А1В1 = АВ × cosα
Положение прямых в пространстве (относительно плоскостей проекций)
на комплексном чертеже
определяют их графические признаки
Прямые
общего положения частного положения
Уровня
параллельны одной из плоскостей проекций
Проецирующие
перпендикулярны одной из плоскостей проекций
Вx
Вx
B0
ни одна из проекций
не параллельна
и не перпендикулярна
ни одной из плоскостей
проекций
α
Слайд 9
Так как две точки однозначно определяют положение прямой в
Слайд 11
Прямая частного положения (или прямая уровня) –
прямая, параллельная
Прямая, параллельная горизонтальной плоскости проекций, называется горизонталью - h. На горизонтальную плоскость проекций горизонталь проецируется в натуральную величину. Графический признак горизонтали – z=const.
Слайд 12
Прямая, параллельная фронтальной плоскости проекций, называется
Графический признак фронтали – y=const.
Слайд 13
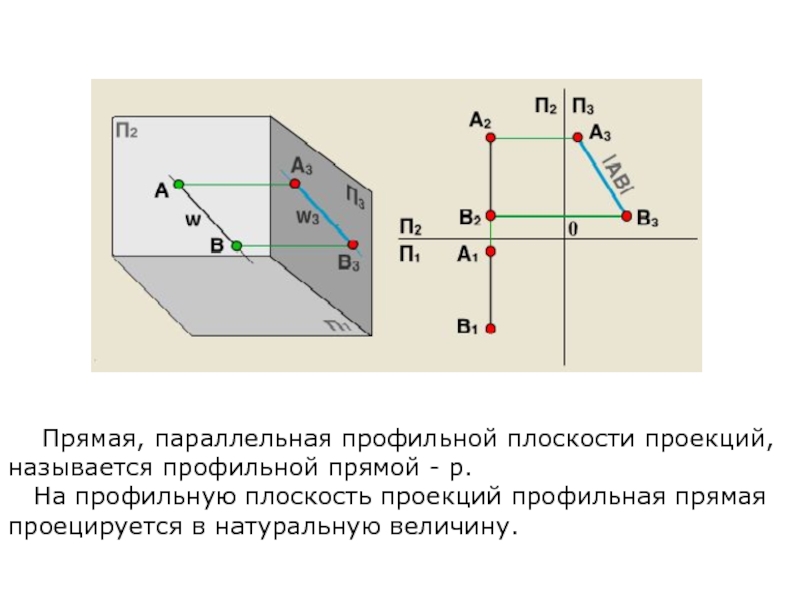
Прямая, параллельная профильной плоскости проекций, называется
На профильную плоскость проекций профильная прямая проецируется в натуральную величину.
Слайд 14
Горизонтально проецирующая прямая – прямая, перпендикулярная
Прямая называется проецирующей, если она перпендикулярна одной из плоскостей проекций. Одна из проекций такой прямой есть точка.
Слайд 15
Фронтально проецирующая прямая – прямая, перпендикулярная
Слайд 16
Профильно проецирующая прямая – прямая, перпендикулярная
Слайд 18взаимное положение
точки и прямой
В тех случаях когда точка и
Слайд 19
х
А2
В2
С2
С1
А1
В1
х
А2
В2
С2
С1
А1
В1
х
А2
D2
С2
С1
А1
В1
В2
D2
//
//
//
//
1. Тремя точками, не лежащими на одной прямой
2. Прямой и точкой
3. Параллельными прямыми
Δ(А; В; С)
Δ(А; ВС)
Δ(АВ ll СD)
Способы задания плоскости в пространстве
Способы задания плоскости на эпюре
Слайд 20
х
А2
В2
С2
С1
А1
В1
Δ(АВ∩BС)
х
А2
В2
С2
С1
А1
В1
Δ( АВС)
4. Пересекающимися прямыми
5. Плоской фигурой (отсеком плоскости)
6. Следами
х
Px
Pz
Py
Py
pП1
pП2
z
y
Δ(АВ∩ВС)
Δ(ΔАВС)
Δ(рП1; рП2;
pП3
Способы задания плоскости в пространстве
Способы задания плоскости на эпюре
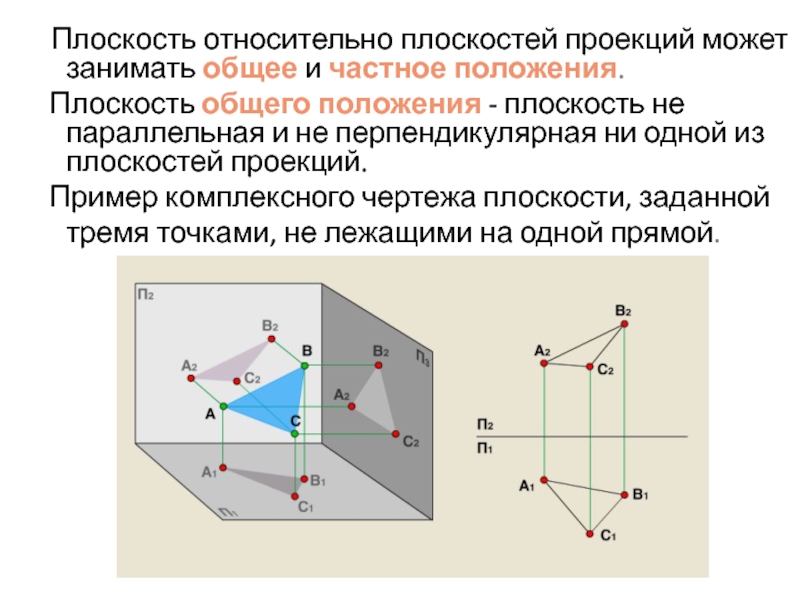
Слайд 21 Плоскость относительно плоскостей проекций может занимать общее и
Плоскость общего положения - плоскость не параллельная и не перпендикулярная ни одной из плоскостей проекций.
Пример комплексного чертежа плоскости, заданной тремя точками, не лежащими на одной прямой.
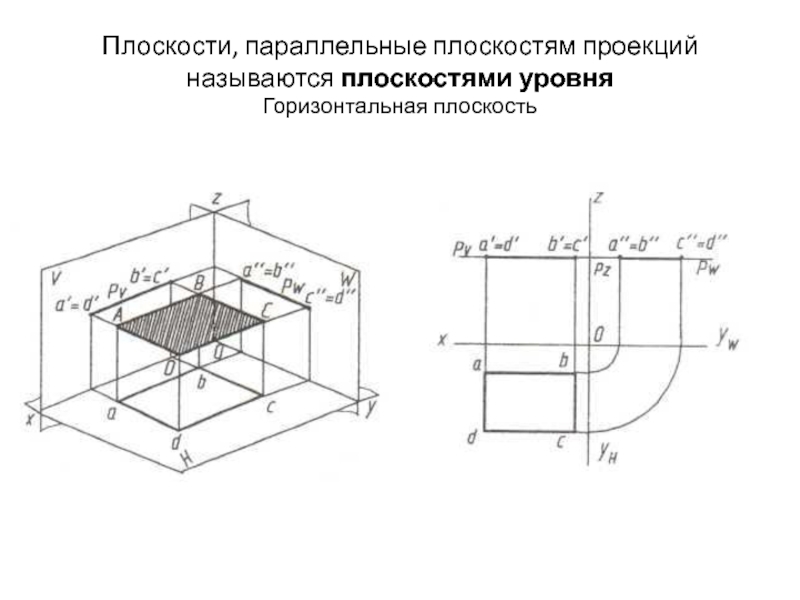
Слайд 22Плоскости, параллельные плоскостям проекций называются плоскостями уровня
Горизонтальная плоскость
Слайд 27
х
А2
В2
С2
С1
А1
В1
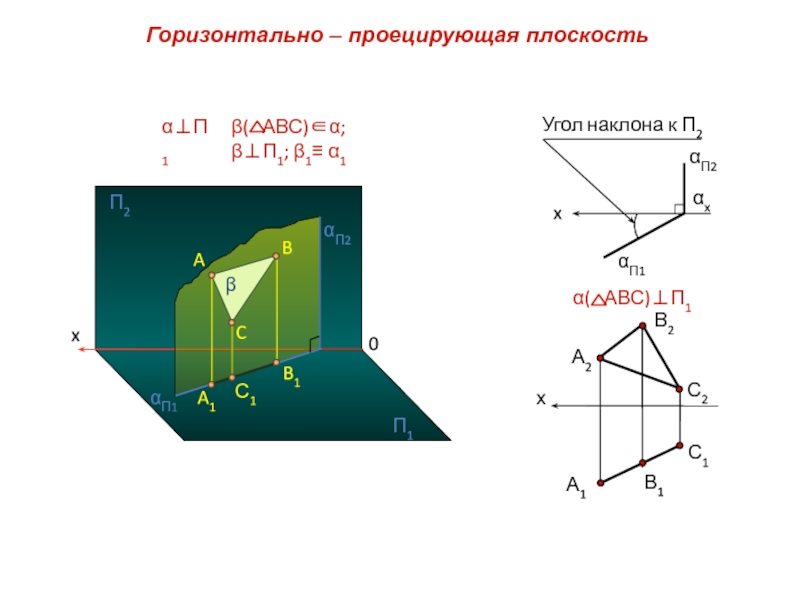
α( АВС)⊥П1
Горизонтально – проецирующая плоскость
x
αП1
αx
Угол наклона к П2
x
A1
B1
A
0
B
C
αП2
С1
П2
П1
α⊥П1
β
β( АВС)∈α; β⊥П1; β1≡ α1
αП1
αП2
Слайд 30
За основные плоскости