Проекции плоскости (Лекция 3) презентация

Содержание

Способы задания плоскости На комплексном чертеже плоскость Σ можно задать: 1) проекциями трех точек, не лежащих на одной прямой; 2) проекциями прямой и точки, взятой вне этой прямой; 3) проекциями двух

Слайд 1Проекции плоскости
Лекция 3

Слайд 2Способы задания плоскости
На комплексном чертеже плоскость Σ можно задать: 1) проекциями

трех точек, не лежащих на одной прямой; 2) проекциями прямой и точки, взятой вне этой прямой; 3) проекциями двух пересекающихся прямых; 4) проекциями двух параллельных прямых;

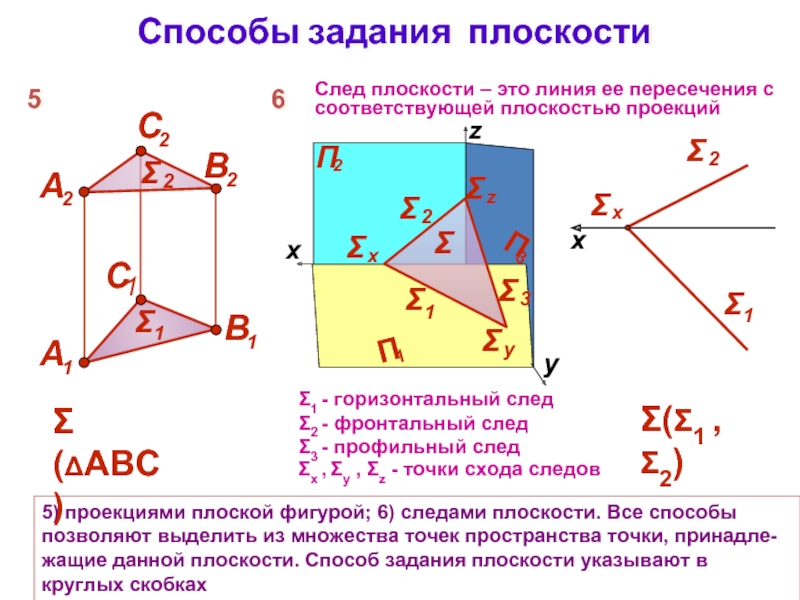
Слайд 3Способы задания плоскости
5) проекциями плоской фигурой; 6) следами плоскости. Все способы

позволяют выделить из множества точек пространства точки, принадле-жащие данной плоскости. Способ задания плоскости указывают в круглых скобках

След плоскости – это линия ее пересечения с соответствующей плоскостью проекций

Слайд 4Положение плоскости относительно плоскостей проекций
Плоскость общего положения наклонена ко всем плоскостям

проекций

Плоскость частного положения перпендикулярна или параллельна одной из плоскостей проекций

Горизонтально проецирующая плоскость ⊥ П1
Фронтально проецирующая плоскость ⊥ П2 Профильно проецирующая плоскость ⊥ П3

Горизонтальная плоскость ⎢⎢ П1
Фронтальная плоскость ⎢⎢ П2
Профильная плоскость ⎢⎢П3

Плоскость, перпендикулярная одной из плоскостей проекций, называется проецирующей плоскостью:

Плоскость, параллельная плоскости проекций, назы-вается плоскостью уровня (дважды проецирующей):

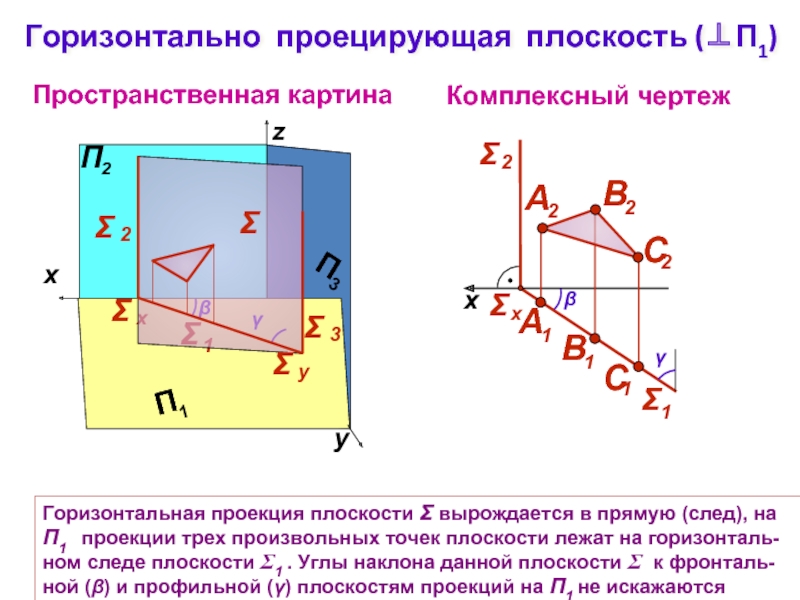
Слайд 5Горизонтально проецирующая плоскость (⊥П1)
Пространственная картина
Комплексный чертеж
y
z
Горизонтальная проекция плоскости Σ вырождается в

прямую (след), на П1 проекции трех произвольных точек плоскости лежат на горизонталь-ном следе плоскости Σ1 . Углы наклона данной плоскости Σ к фронталь-ной (β) и профильной (γ) плоскостям проекций на П1 не искажаются


β


γ


Σ

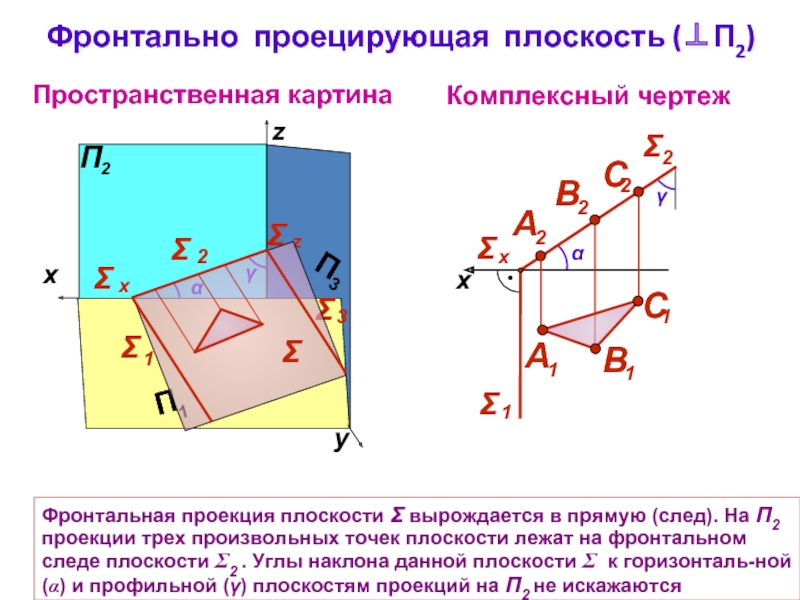
Слайд 6Фронтально проецирующая плоскость (⊥П2)
Комплексный чертеж
y
z
Пространственная картина


γ
α

Σ
Фронтальная проекция плоскости Σ вырождается в

прямую (след). На П2 проекции трех произвольных точек плоскости лежат на фронтальном следе плоскости Σ2 . Углы наклона данной плоскости Σ к горизонталь-ной (α) и профильной (γ) плоскостям проекций на П2 не искажаются

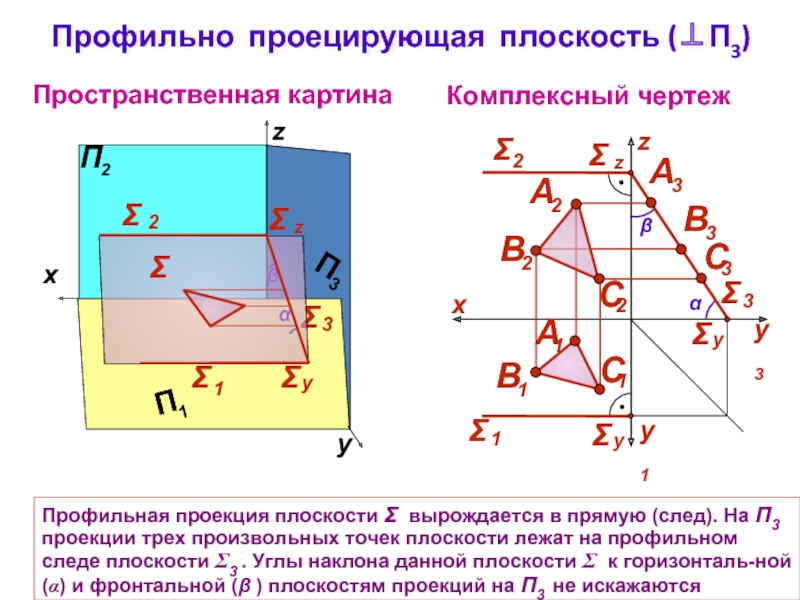
Слайд 7Профильно проецирующая плоскость (⊥П3)
Комплексный чертеж
z
Пространственная картина


α
β

Σ
Профильная проекция плоскости Σ вырождается в

прямую (след). На П3 проекции трех произвольных точек плоскости лежат на профильном следе плоскости Σ3 . Углы наклона данной плоскости Σ к горизонталь-ной (α) и фронтальной (β ) плоскостям проекций на П3 не искажаются

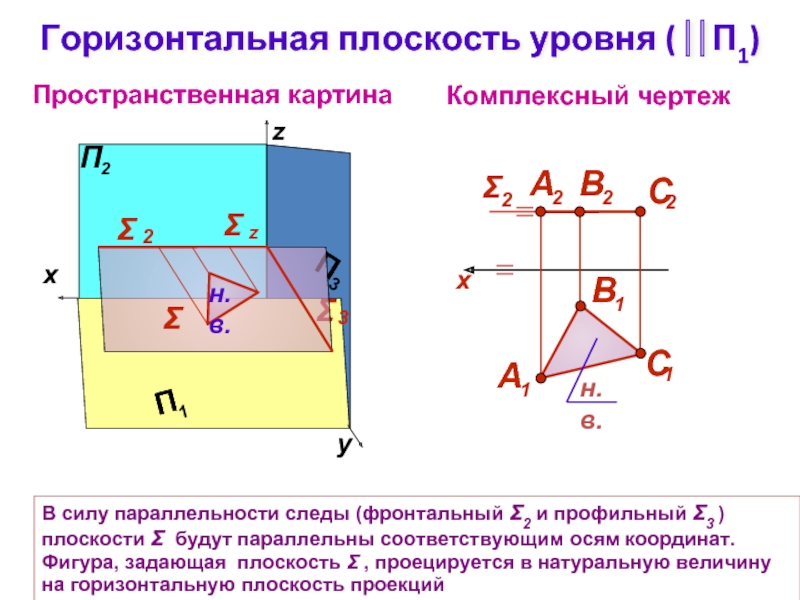
Слайд 8Горизонтальная плоскость уровня ( ⎢⎢П1)
Комплексный чертеж
z

Σ
Пространственная картина
В силу параллельности следы (фронтальный

Σ2 и профильный Σ3 ) плоскости Σ будут параллельны соответствующим осям координат. Фигура, задающая плоскость Σ , проецируется в натуральную величину на горизонтальную плоскость проекций

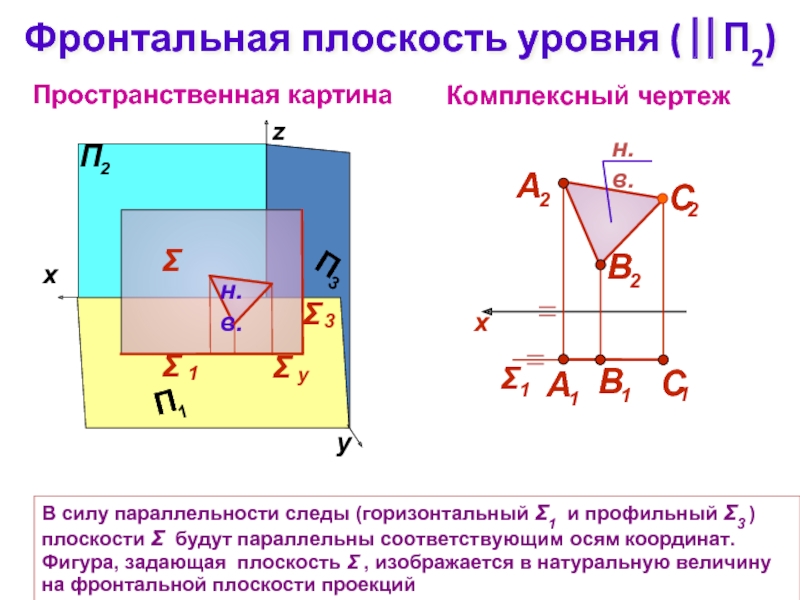
Слайд 9Фронтальная плоскость уровня ( ⎢⎢П2)
Комплексный чертеж
z

Пространственная картина
Σ
В силу параллельности следы (горизонтальный

Σ1 и профильный Σ3 ) плоскости Σ будут параллельны соответствующим осям координат. Фигура, задающая плоскость Σ , изображается в натуральную величину на фронтальной плоскости проекций

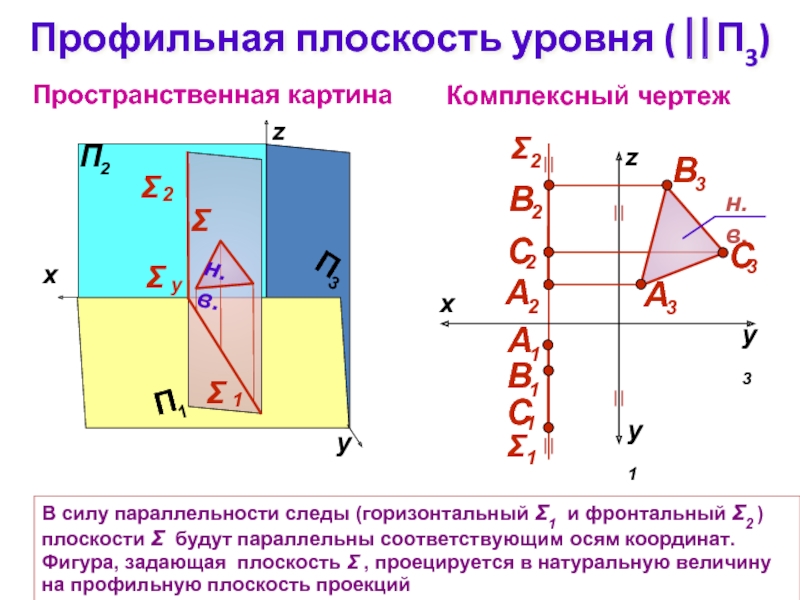
Слайд 10Профильная плоскость уровня ( ⎢⎢П3)
Комплексный чертеж
z

Пространственная картина
Σ
В силу параллельности следы (горизонтальный

Σ1 и фронтальный Σ2 ) плоскости Σ будут параллельны соответствующим осям координат. Фигура, задающая плоскость Σ , проецируется в натуральную величину на профильную плоскость проекций

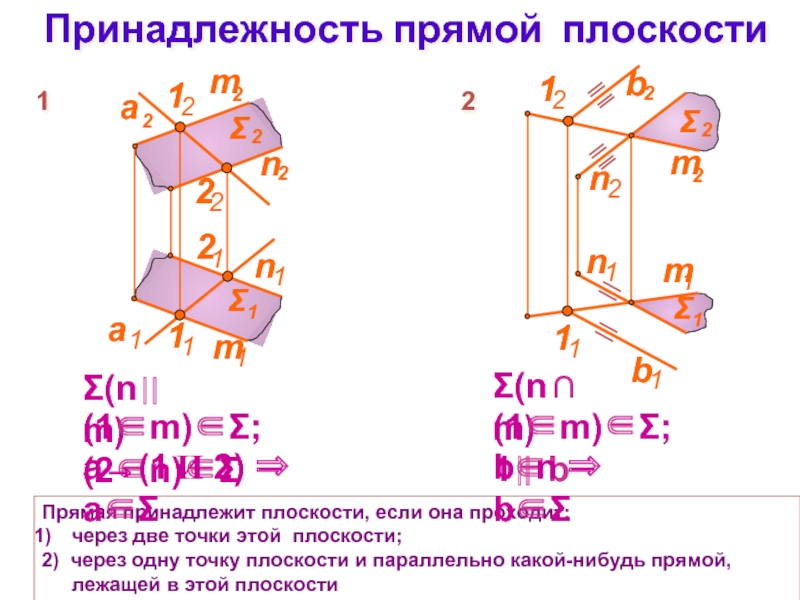
Слайд 11Принадлежность прямой плоскости
Прямая принадлежит плоскости, если она проходит:
через две точки

этой плоскости;
2) через одну точку плоскости и параллельно какой-нибудь прямой, лежащей в этой плоскости

Σ(n⎟⎟ m)

1

(1∈m)∈Σ; (2∈n)∈Σ

а→(1 И 2) ⇒ а∈Σ

2

Σ(n ∩ m)









(1∈m)∈Σ; 1∈b

b⎟⎟ n ⇒ b∈Σ

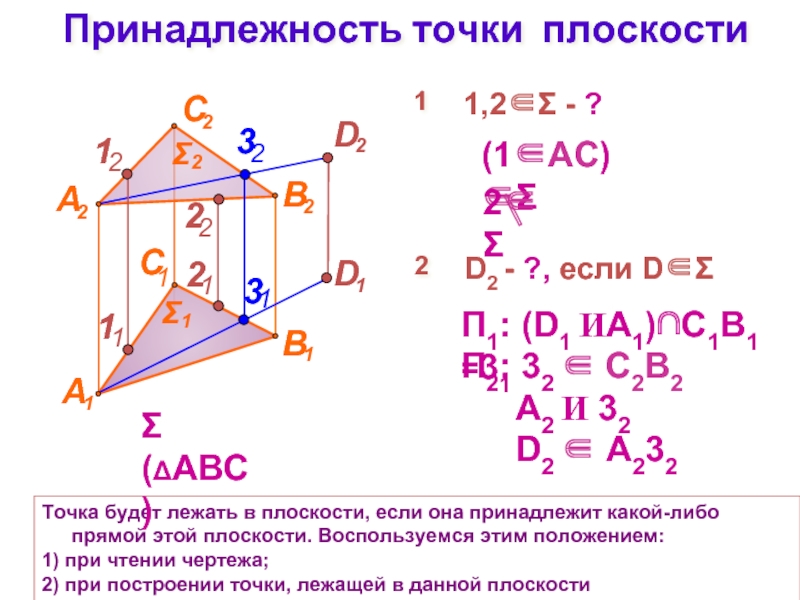
Слайд 12Принадлежность точки плоскости
Точка будет лежать в плоскости, если она принадлежит какой-либо

прямой этой плоскости. Воспользуемся этим положением:
1) при чтении чертежа;
2) при построении точки, лежащей в данной плоскости

(1∈АС)∈Σ

П1: (D1 ИA1)∩С1В1 =31



Σ(ΔАВС)






1


П2: 32 ∈ C2B2

1,2∈Σ - ?

А2 И 32

D2 ∈ А232


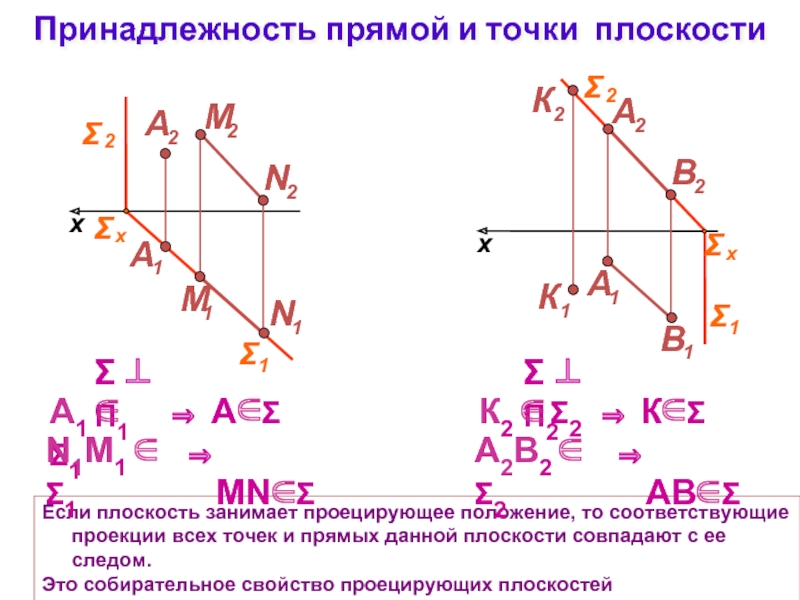
Слайд 13Принадлежность прямой и точки плоскости
Если плоскость занимает проецирующее положение, то соответствующие

проекции всех точек и прямых данной плоскости совпадают с ее следом.
Это собирательное свойство проецирующих плоскостей

Σ ⊥ П1

x


Σ ⊥ П2

x


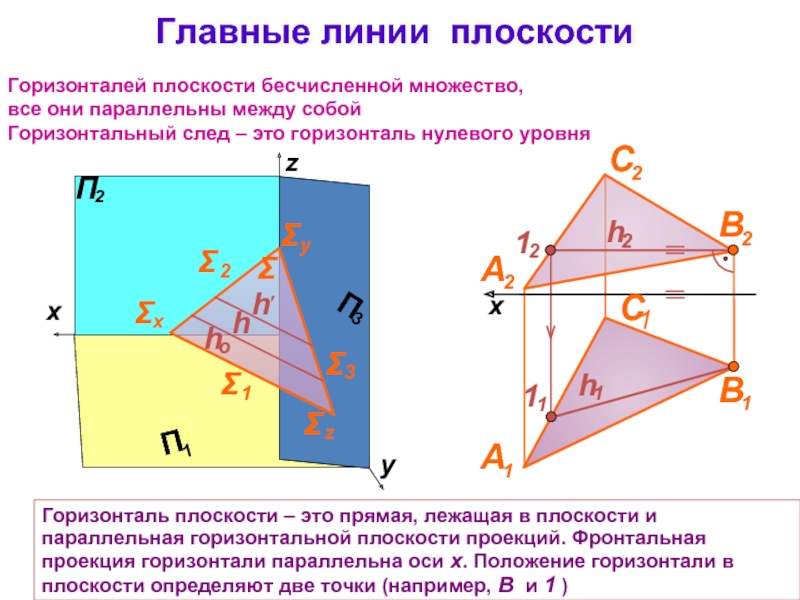
Слайд 14Главные линии плоскости
Горизонталь плоскости – это прямая, лежащая в плоскости и

параллельная горизонтальной плоскости проекций. Фронтальная проекция горизонтали параллельна оси x. Положение горизонтали в плоскости определяют две точки (например, В и 1 )


Σ

Горизонталей плоскости бесчисленной множество,
все они параллельны между собой
Горизонтальный след – это горизонталь нулевого уровня








x

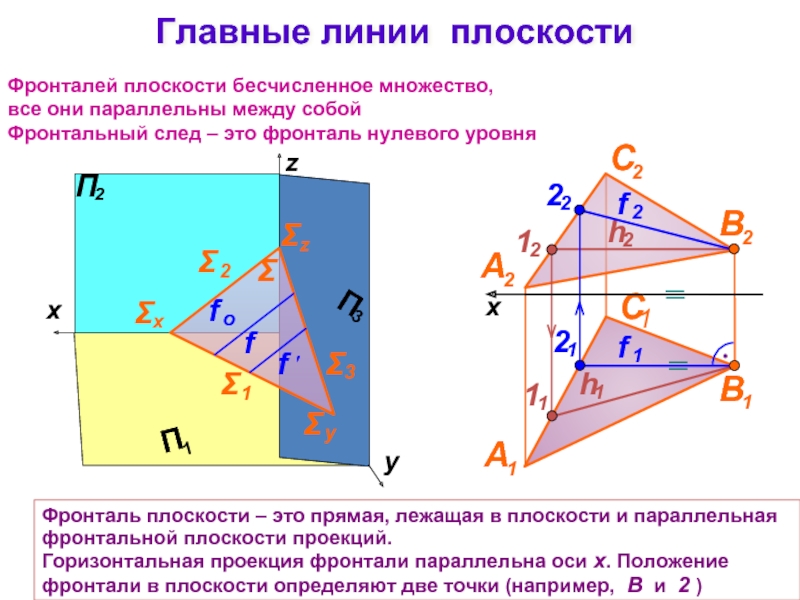
Слайд 15Главные линии плоскости

Σ
Фронталей плоскости бесчисленное множество,
все они параллельны между собой
Фронтальный след

– это фронталь нулевого уровня

Фронталь плоскости – это прямая, лежащая в плоскости и параллельная фронтальной плоскости проекций.
Горизонтальная проекция фронтали параллельна оси x. Положение фронтали в плоскости определяют две точки (например, В и 2 )










x

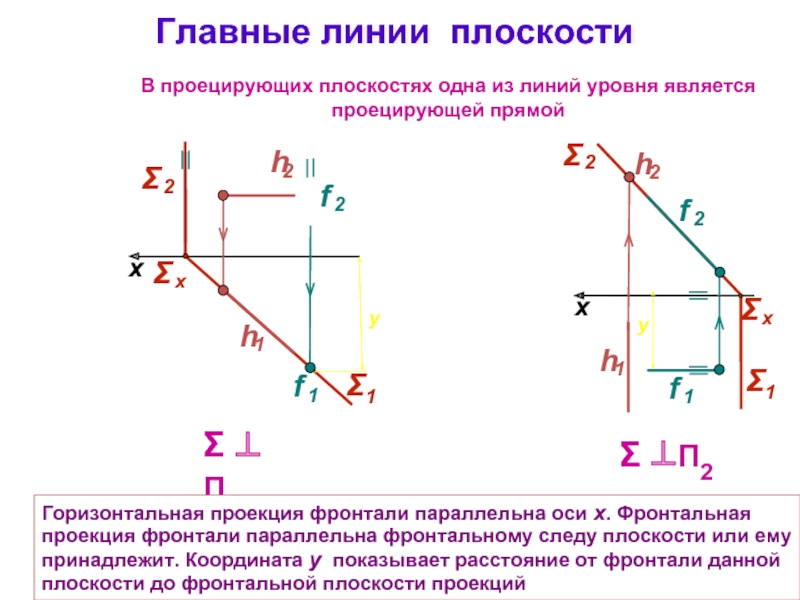
Слайд 16Главные линии плоскости
Σ ⊥ П1
x

Σ ⊥П2

x
В проецирующих плоскостях одна из линий

уровня является проецирующей прямой

Горизонтальная проекция фронтали параллельна оси x. Фронтальная проекция фронтали параллельна фронтальному следу плоскости или ему принадлежит. Координата y показывает расстояние от фронтали данной плоскости до фронтальной плоскости проекций

Слайд 17А1
А2
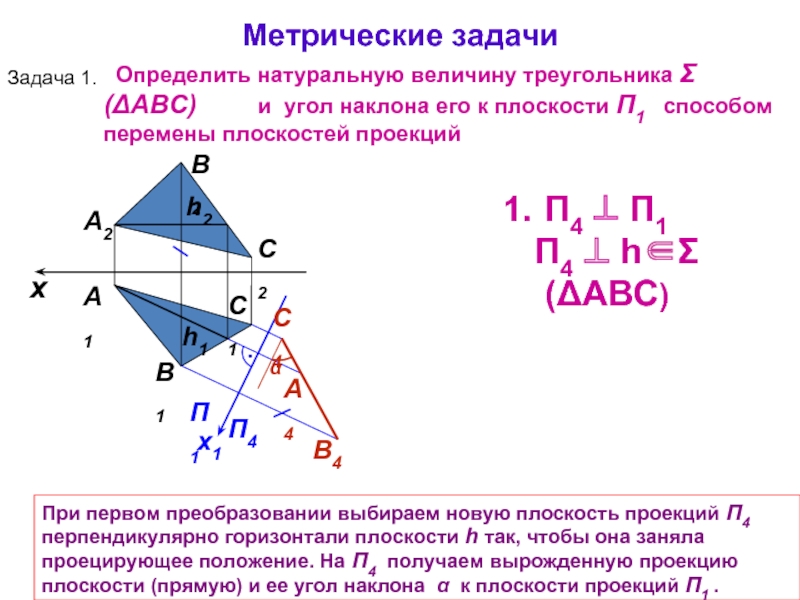
При первом преобразовании выбираем новую плоскость проекций П4 перпендикулярно горизонтали

плоскости h так, чтобы она заняла проецирующее положение. На П4 получаем вырожденную проекцию плоскости (прямую) и ее угол наклона α к плоскости проекций П1 .

Определить натуральную величину треугольника Σ(ΔАВС) и угол наклона его к плоскости П1 способом перемены плоскостей проекций



B1

C2

B2

C1

x

П4 ⊥ П1
П4 ⊥ h∈Σ(ΔАВС)

Метрические задачи

Задача 1.

Слайд 18x
А1
А2

П1
П4
x1
П4 ⊥ П1
П4 ⊥ h∈Σ(ΔАВС)
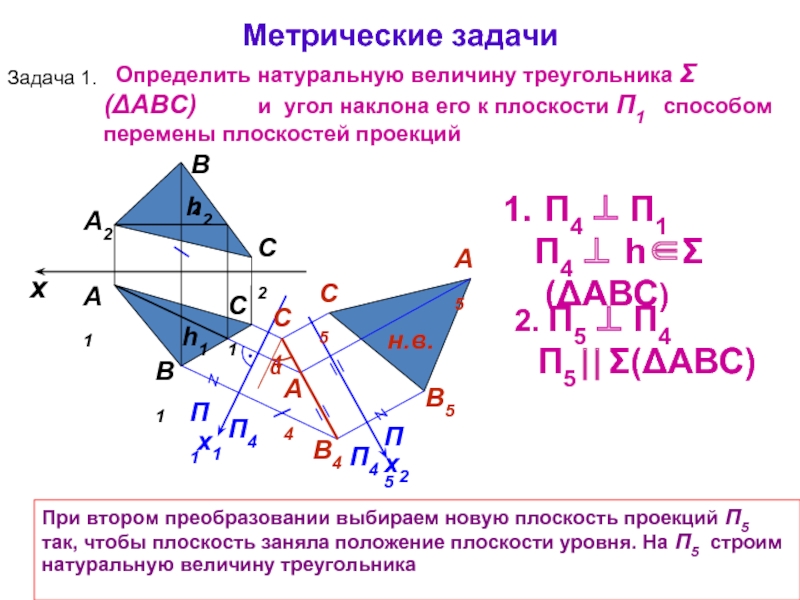
2. П5 ⊥ П4

П5⎟⎟ Σ(ΔАВС)

При втором преобразовании выбираем новую плоскость проекций П5 так, чтобы плоскость заняла положение плоскости уровня. На П5 строим натуральную величину треугольника



h1

h2

B1

C2

B2

А4

C1

В4

C4


α

Метрические задачи

Задача 1.

Определить натуральную величину треугольника Σ(ΔАВС) и угол наклона его к плоскости П1 способом перемены плоскостей проекций

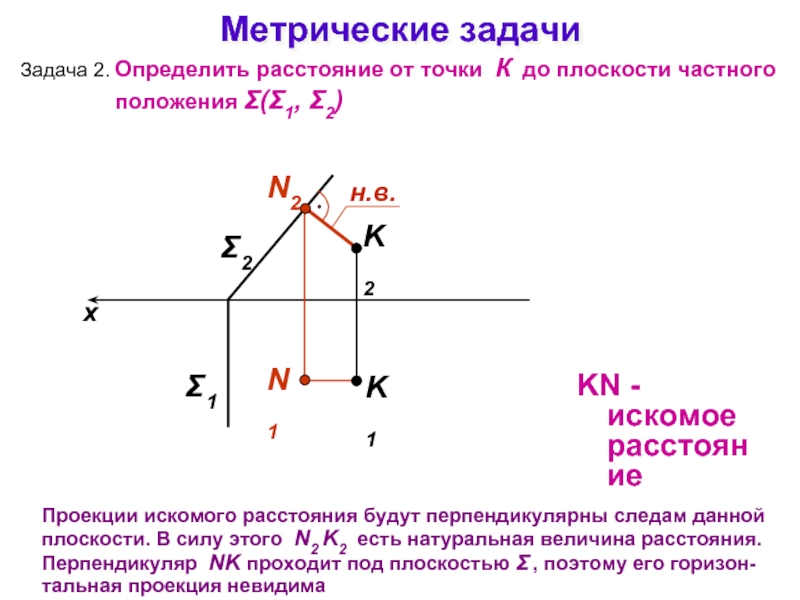
Слайд 19Метрические задачи
Задача 2.
Определить расстояние от точки К до плоскости частного положения

Σ(Σ1, Σ2)

x

Проекции искомого расстояния будут перпендикулярны следам данной плоскости. В силу этого N2 K2 есть натуральная величина расстояния. Перпендикуляр NK проходит под плоскостью Σ , поэтому его горизон-тальная проекция невидима

Σ 2

K1


Σ 1

K2


KN - искомое расстояние

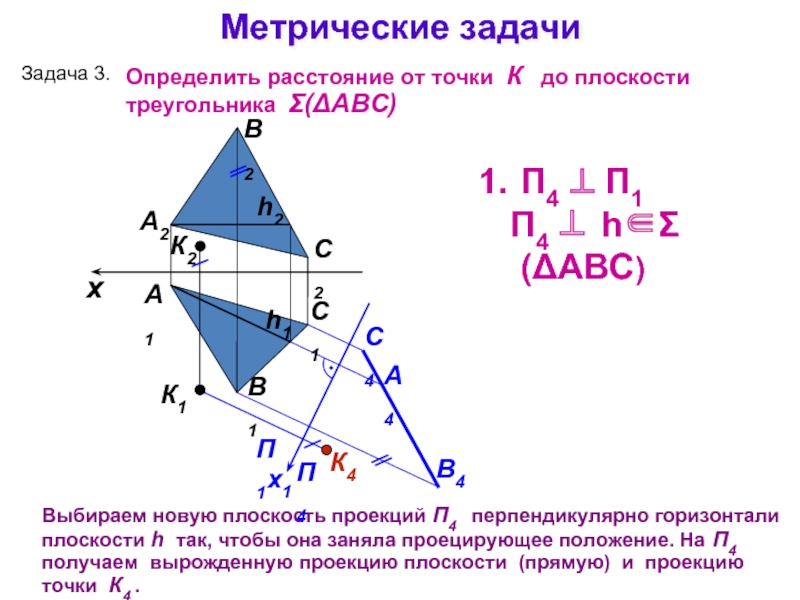
Слайд 20Метрические задачи
А1
А2
Выбираем новую плоскость проекций П4 перпендикулярно горизонтали плоскости h

так, чтобы она заняла проецирующее положение. На П4 получаем вырожденную проекцию плоскости (прямую) и проекцию точки К4 .

Задача 3.



B1

C2

B2

C1

x

П4 ⊥ П1
П4 ⊥ h∈Σ(ΔАВС)


К1

К2


Определить расстояние от точки К до плоскости треугольника Σ(ΔАВС)

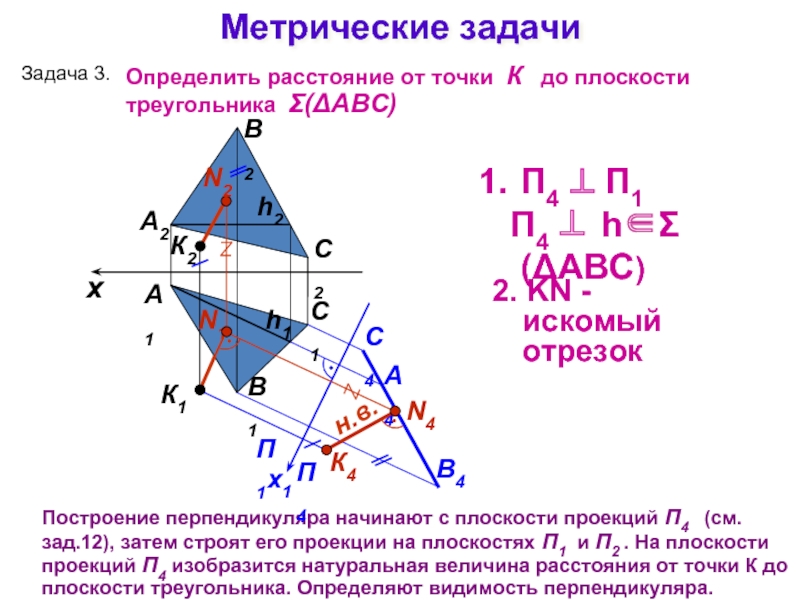
Слайд 21А1
А2
Построение перпендикуляра начинают с плоскости проекций П4 (см. зад.12), затем

строят его проекции на плоскостях П1 и П2 . На плоскости проекций П4 изобразится натуральная величина расстояния от точки К до плоскости треугольника. Определяют видимость перпендикуляра.



B1

C2

B2

C1

x

П4 ⊥ П1
П4 ⊥ h∈Σ(ΔАВС)

2. KN - искомый отрезок

К1

К2



Метрические задачи

Задача 3.

Определить расстояние от точки К до плоскости треугольника Σ(ΔАВС)

Похожие презентации

risuem oduvanchiki 285
prezentatsiya druzhba 310
detyam o narodnom dekorativno prikladnom iskusstve1 336
prezentatsiya k uroku raduga - duga 309
Архитектура. Построение плана здания 416
Комплексный чертеж прямой, кривой линии 421

Обратная связь

Если не удалось найти и скачать презентацию, Вы можете заказать его на нашем сайте. Мы постараемся найти нужный Вам материал и отправим по электронной почте. Не стесняйтесь обращаться к нам, если у вас возникли вопросы или пожелания:

Email: Нажмите что бы посмотреть 

Что такое ThePresentation.ru?

Это сайт презентаций, докладов, проектов, шаблонов в формате PowerPoint. Мы помогаем школьникам, студентам, учителям, преподавателям хранить и обмениваться учебными материалами с другими пользователями.

Для правообладателей

Яндекс.Метрика