Л.Ю.
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Поверхности. Способы задания поверхностей. Классификация поверхностей. Многогранники. Поверхности вращения второго порядка презентация
Содержание
- 1. Поверхности. Способы задания поверхностей. Классификация поверхностей. Многогранники. Поверхности вращения второго порядка
- 2. ПОВЕРХНОСТЬ МНОЖЕСТВО ПОЛОЖЕНИЙ ЛИНИИ ПЕРЕМЕЩАЮЩЕЙСЯ В ПРОСТРАНСТВЕ ПО ОПРЕДЕЛЕННОМУ ЗАКОНУ
- 3. Направляющая Образующая
- 4. СПОСОБЫ ЗАДАНИЯ ПОВЕРХНОСТЕЙ АНАЛИТИЧЕСКИЙ –
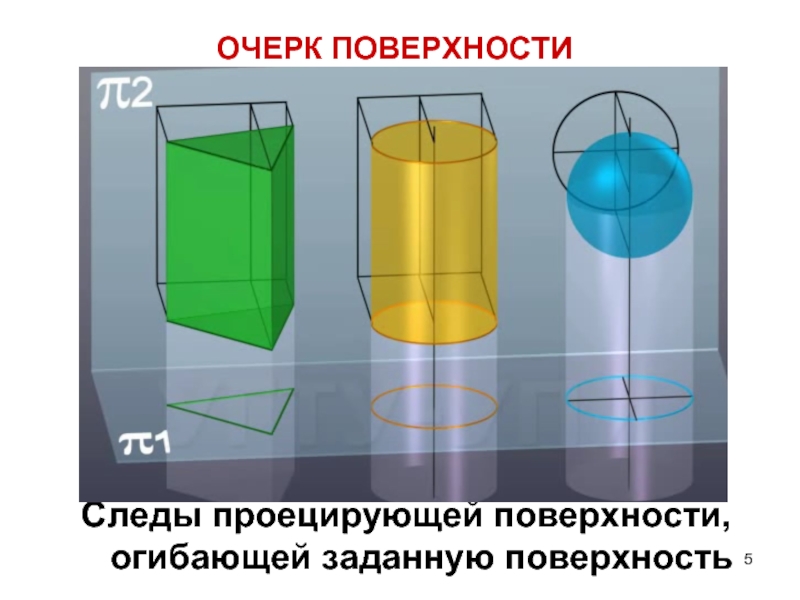
- 5. ОЧЕРК ПОВЕРХНОСТИ Следы проецирующей поверхности, огибающей заданную поверхность
- 6. П1 Очерк поверхности на плоскости Огибающая цилиндрическая поверхность Поверхность (каркас) Лекция 4. Поверхности
- 7. КАРКАС ПОВЕРХНОСТИ ТОЧЕЧНЫЙ КАРКАС- множество точек принадлежащих поверхности В этом случае поверхность аппроксимируется поверхностью многогранника
- 8. Каркас множество линий, заполняющих поверхность так, что
- 9. Ф(L,k)(A) ОПРЕДЕЛИТЕЛЬ ПОВЕРХНОСТИ L k ОПРЕДЕЛИТЕЛЬ совокупность
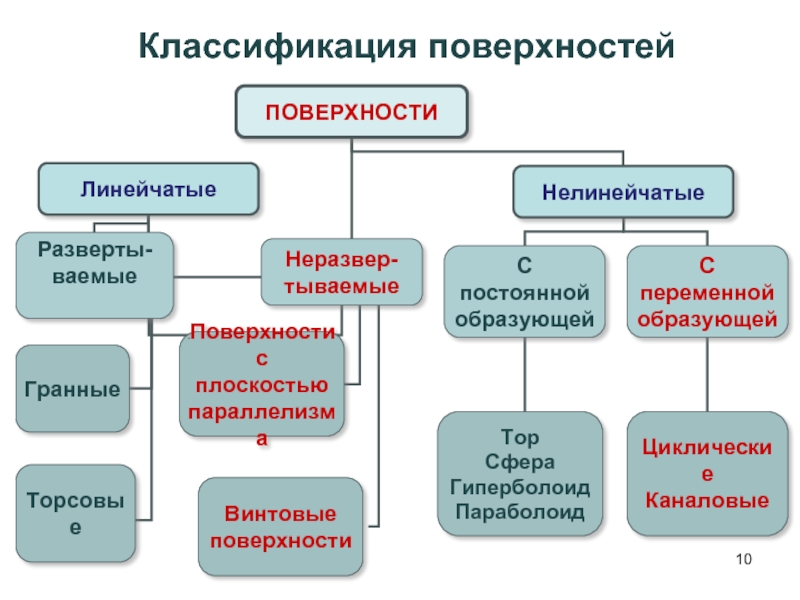
- 10. Классификация поверхностей
- 11. Гранные поверхности Призма - образуется при движении
- 12. Гранные поверхности Пирамида – образуется при движении
- 13. ПРОСТЕЙШИЕ ПОВЕРХНОСТИ ВРАЩЕНИЯ m - ОБРАЗУЮЩАЯ ПОВЕРХНОСТИ
- 14. ЦИЛИНДРИЧЕСКАЯ ПОВЕРХНОСТЬ ВРАЩЕНИЯ i – ось
- 15. ПОВЕРХНОСТЬ КОНУСА ВРАЩЕНИЯ 1. i –
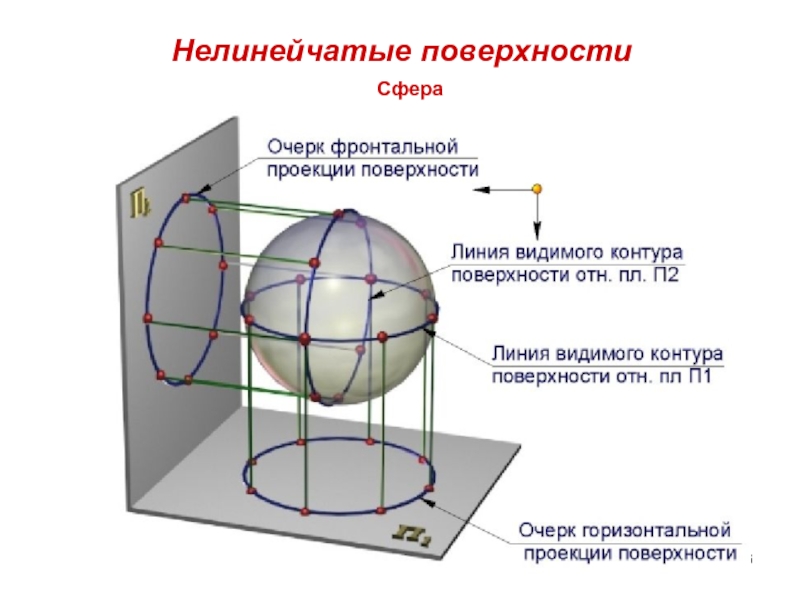
- 16. Нелинейчатые поверхности Сфера
- 17. ПОВЕРХНОСТЬ CФЕРЫ I – ось
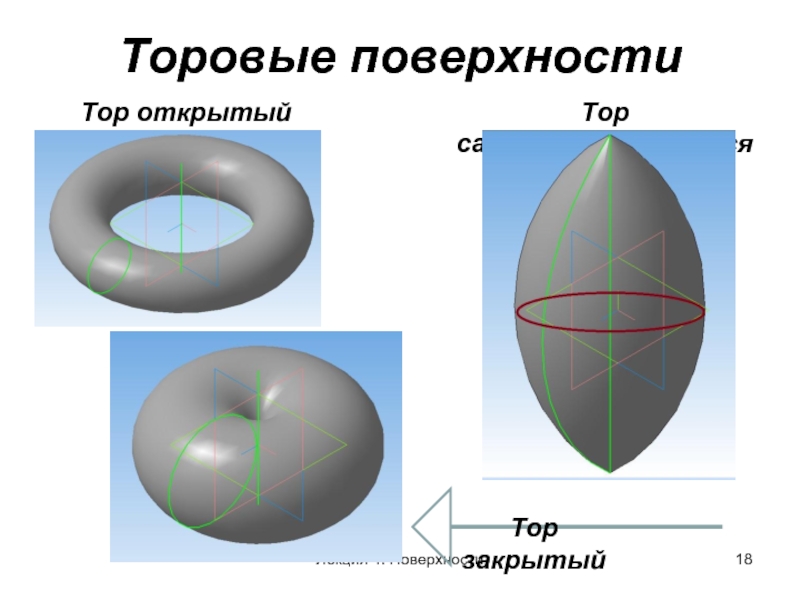
- 18. Торовые поверхности Тор открытый Лекция 4. Поверхности Тор самопересекающийся
- 19. Торовая поверхность ОТКРЫТЫЙ ТОР i
- 20. Торовая поверхность ЗАКРЫТЫЙ ТОР
- 21. Торовая поверхность САМОПЕРЕСЕКАЮЩИЙСЯ ТОР (тор -
- 22. Коническая поверхность Торсовые поверхности X
- 23. Торсовая поверхность X m2 m1
- 24. Поверхности Каталана (с плоскостью параллелизма) Цилиндроид Коноид Гиперболический параболоид (косая плоскость)
- 25. Поверхности c плоскостью параллелизма Цилиндроид X
- 26. Коноид Поверхности c плоскостью параллелизма X
- 27. Косая плоскость (гиперболический параболоид) Поверхности c плоскостью параллелизма X m2 m1 n2 n1 L2 L1
- 28. ВИНТОВЫЕ ПОВЕРХНОСТИ Прямой и наклонный геликоид –
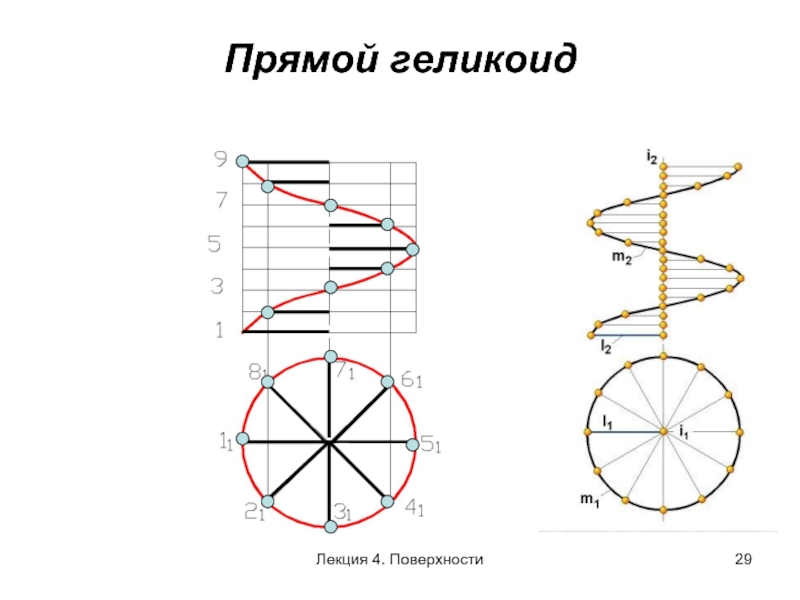
- 29. Прямой геликоид
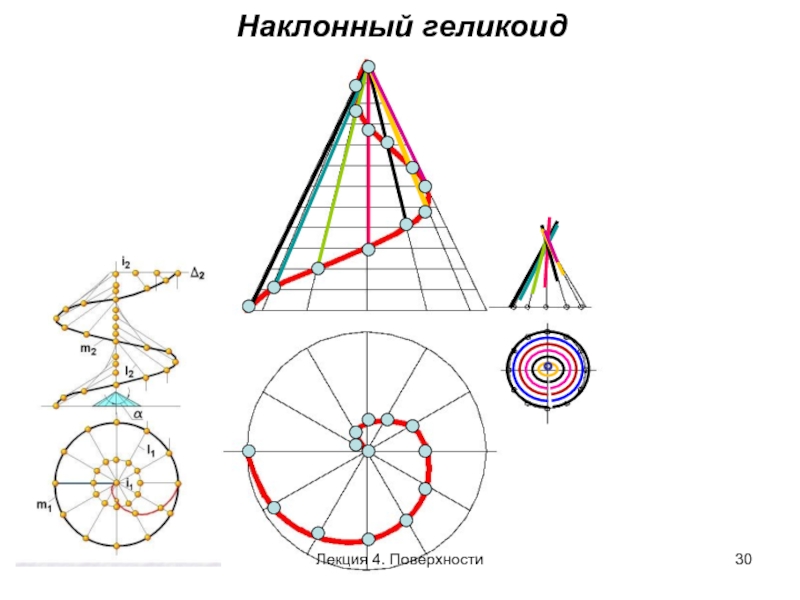
- 30. Наклонный геликоид
- 31. Выводы по теме Поверхностью называется множество положений
- 32. Рекомендованная литература Бударин О. С. Начертательная геометрия.
- 33. Благодарю за внимание Лекция 4. Поверхности
Слайд 1Поверхности
Определение поверхности
Способы задания поверхностей
Классификация поверхностей
Многогранники
Поверхности вращения второго порядка
Лекция 4
Лектор: Стриганова
Слайд 3
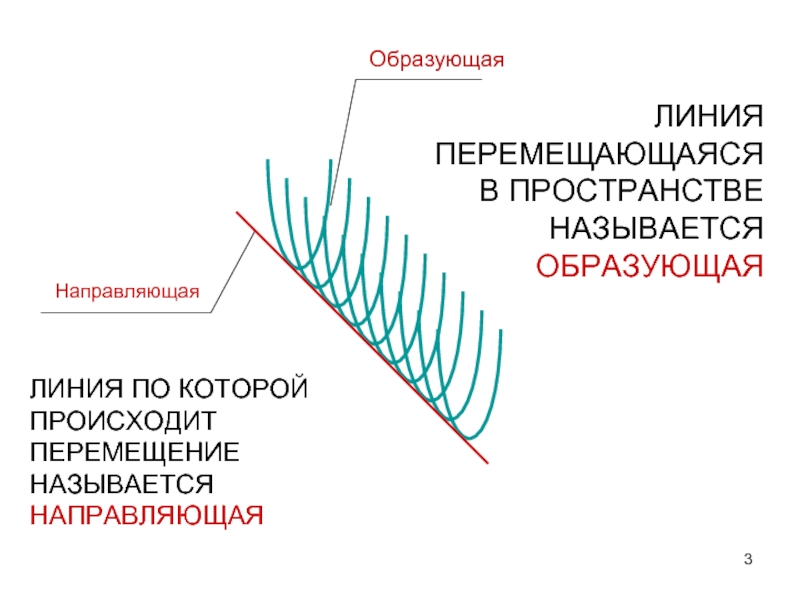
Направляющая
Образующая
ЛИНИЯ ПЕРЕМЕЩАЮЩАЯСЯ В ПРОСТРАНСТВЕ НАЗЫВАЕТСЯ ОБРАЗУЮЩАЯ
ЛИНИЯ ПО КОТОРОЙ ПРОИСХОДИТ ПЕРЕМЕЩЕНИЕ НАЗЫВАЕТСЯ
НАПРАВЛЯЮЩАЯ
Слайд 4СПОСОБЫ ЗАДАНИЯ ПОВЕРХНОСТЕЙ
АНАЛИТИЧЕСКИЙ –
X2 + Y2 + Z2 =1
2. ГРАФИЧЕСКИЙ:
а) очерк
б) каркас
в) определитель
2. ГРАФИЧЕСКИЙ:
а) очерк
б) каркас
в) определитель
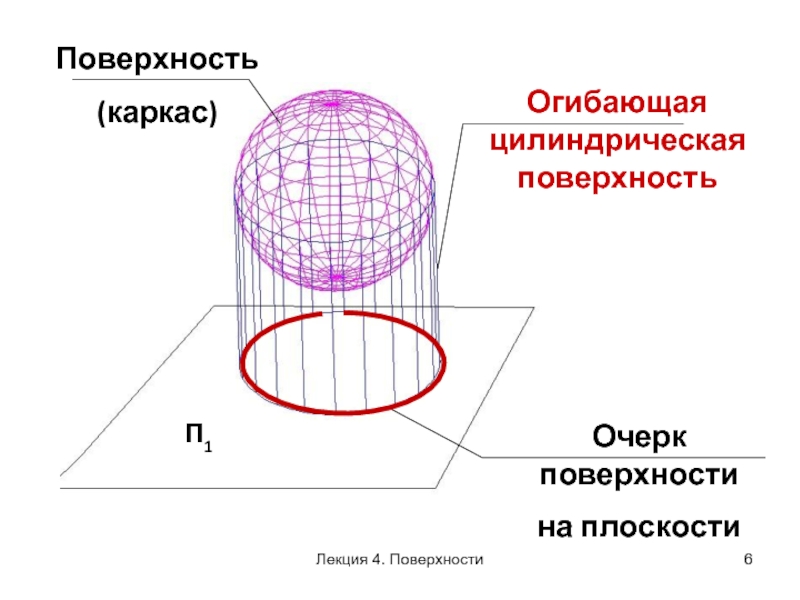
Слайд 6П1
Очерк поверхности
на плоскости
Огибающая цилиндрическая поверхность
Поверхность
(каркас)
Лекция 4. Поверхности
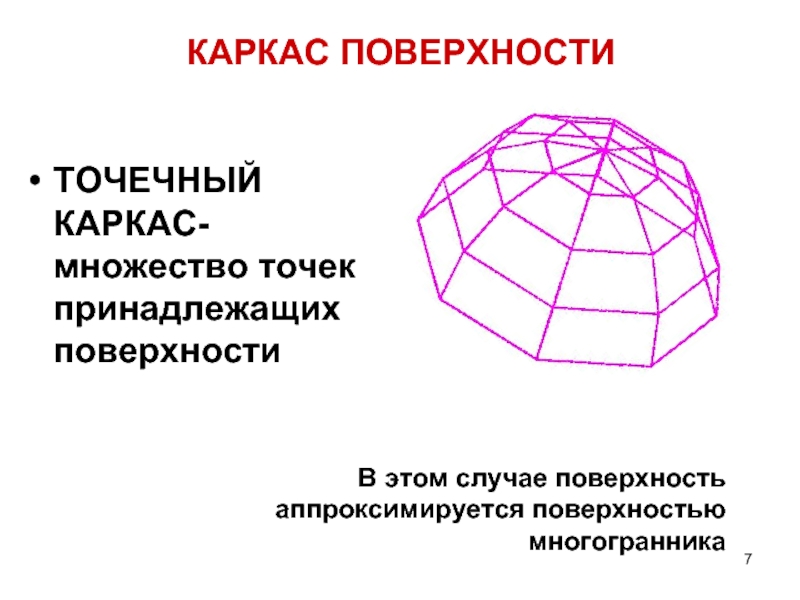
Слайд 7КАРКАС ПОВЕРХНОСТИ
ТОЧЕЧНЫЙ КАРКАС- множество точек принадлежащих поверхности
В этом случае поверхность аппроксимируется
поверхностью многогранника
Слайд 8Каркас множество линий, заполняющих поверхность так, что через каждую точку поверхности
проходит одна линия каркаса
ЛИНЕЙЧАТЫЙ КАРКАС
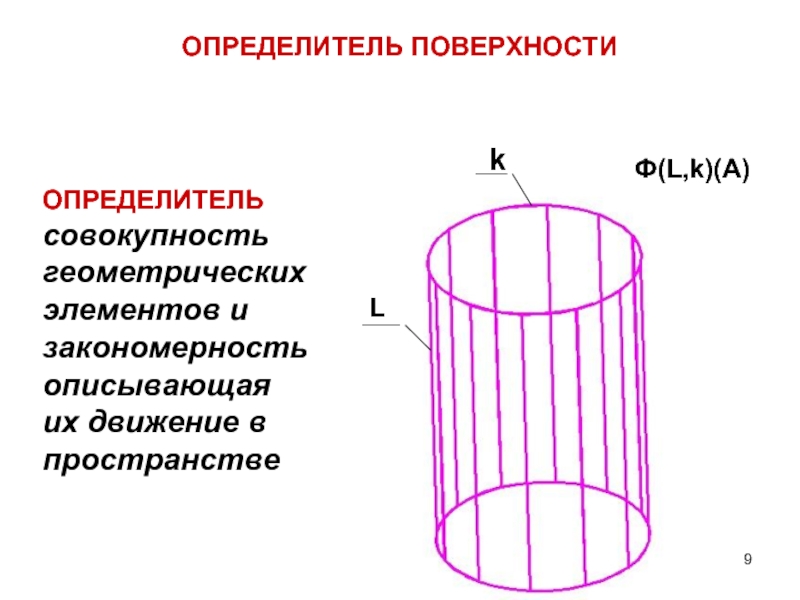
Слайд 9Ф(L,k)(A)
ОПРЕДЕЛИТЕЛЬ ПОВЕРХНОСТИ
L
k
ОПРЕДЕЛИТЕЛЬ совокупность геометрических элементов и закономерность описывающая их движение в
пространстве
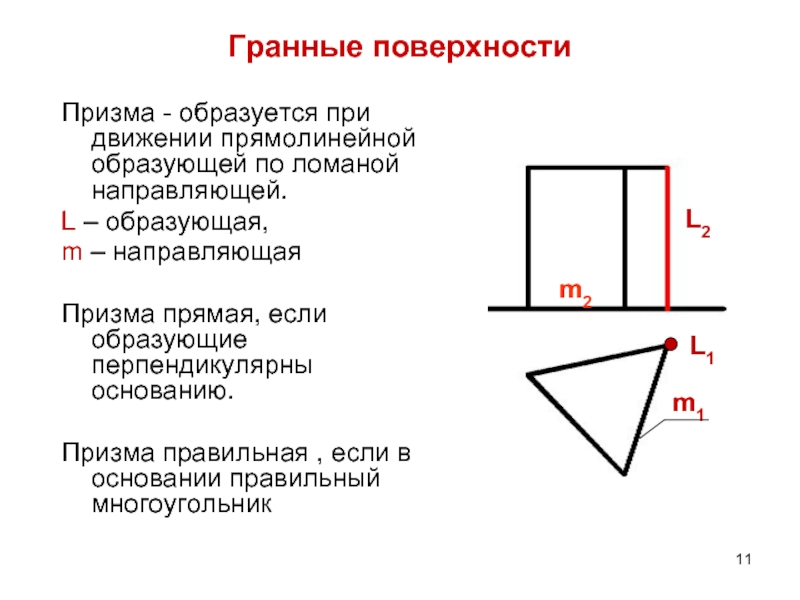
Слайд 11Гранные поверхности
Призма - образуется при движении прямолинейной образующей по ломаной направляющей.
L
– образующая,
m – направляющая
Призма прямая, если образующие перпендикулярны основанию.
Призма правильная , если в основании правильный многоугольник
m – направляющая
Призма прямая, если образующие перпендикулярны основанию.
Призма правильная , если в основании правильный многоугольник
m2
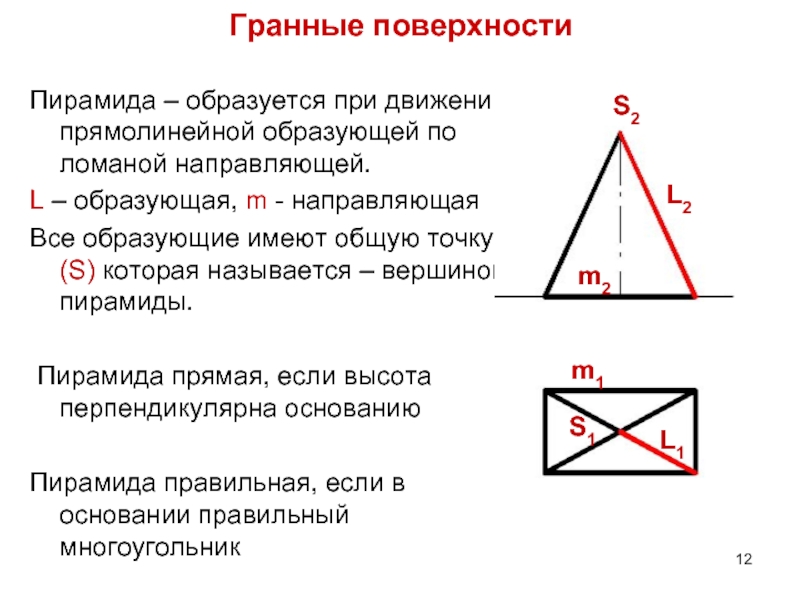
Слайд 12Гранные поверхности
Пирамида – образуется при движении прямолинейной образующей по ломаной направляющей.
L
– образующая, m - направляющая
Все образующие имеют общую точку, (S) которая называется – вершиной пирамиды.
Пирамида прямая, если высота перпендикулярна основанию
Пирамида правильная, если в основании правильный многоугольник
Все образующие имеют общую точку, (S) которая называется – вершиной пирамиды.
Пирамида прямая, если высота перпендикулярна основанию
Пирамида правильная, если в основании правильный многоугольник
m1
m2
L1
S2
S1
L2
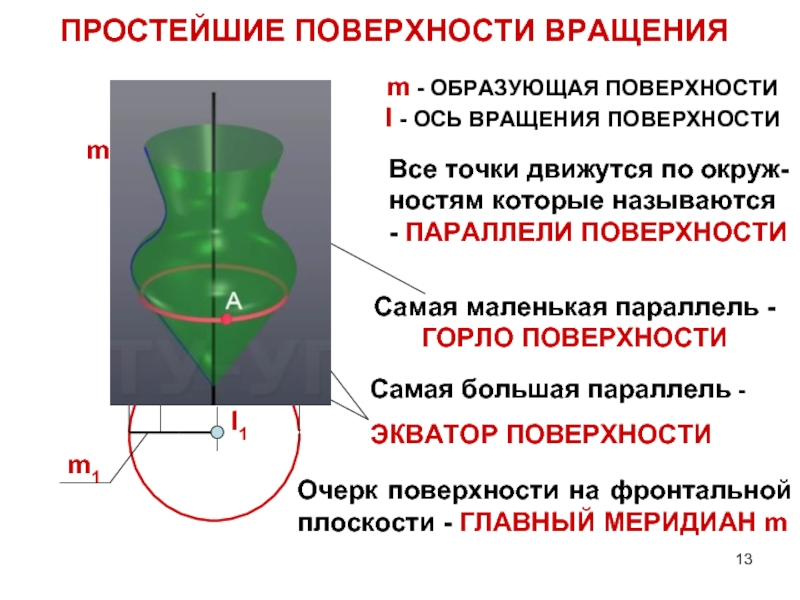
Слайд 13ПРОСТЕЙШИЕ ПОВЕРХНОСТИ ВРАЩЕНИЯ
m - ОБРАЗУЮЩАЯ ПОВЕРХНОСТИ
I - ОСЬ ВРАЩЕНИЯ ПОВЕРХНОСТИ
Самая маленькая
параллель - ГОРЛО ПОВЕРХНОСТИ
Самая большая параллель -
ЭКВАТОР ПОВЕРХНОСТИ
Очерк поверхности на фронтальной плоскости - ГЛАВНЫЙ МЕРИДИАН m
Все точки движутся по окруж- ностям которые называются - ПАРАЛЛЕЛИ ПОВЕРХНОСТИ
m2
m1
I2
I1
Слайд 14
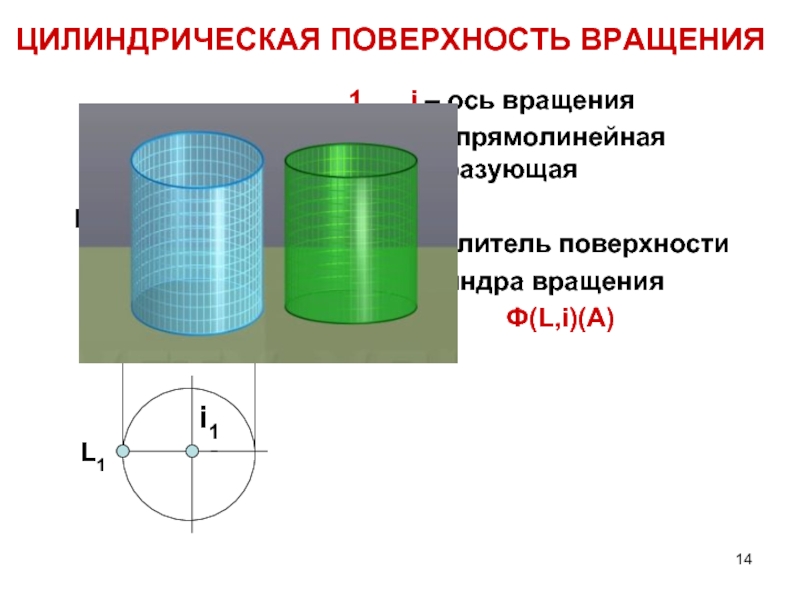
ЦИЛИНДРИЧЕСКАЯ ПОВЕРХНОСТЬ ВРАЩЕНИЯ
i – ось вращения
2. L – прямолинейная образующая
Определитель
поверхности
цилиндра вращения
Ф(L,i)(A)
цилиндра вращения
Ф(L,i)(A)
L2
i2
i1
L1
Слайд 15
ПОВЕРХНОСТЬ КОНУСА ВРАЩЕНИЯ
1. i – ось вращения
2. L – прямолинейная образующая
3.
S – вершина конической поверхности
Определитель поверхности
Ф (L, I, S)(A)
Определитель поверхности
Ф (L, I, S)(A)
L2
L1
i2
i1
S
Слайд 17
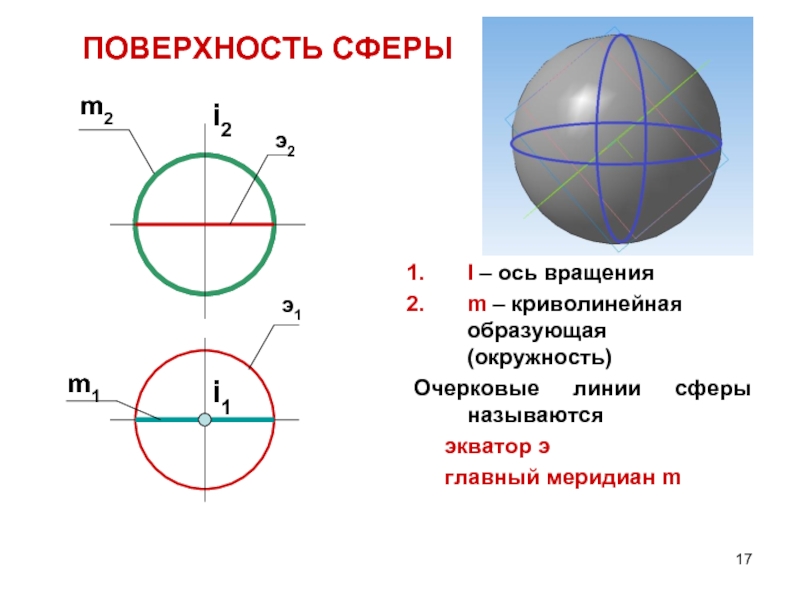
ПОВЕРХНОСТЬ CФЕРЫ
I – ось вращения
m – криволинейная образующая (окружность)
Очерковые линии сферы
называются
экватор э
главный меридиан m
экватор э
главный меридиан m
m2
m1
i2
i1
э2
э1
Слайд 19
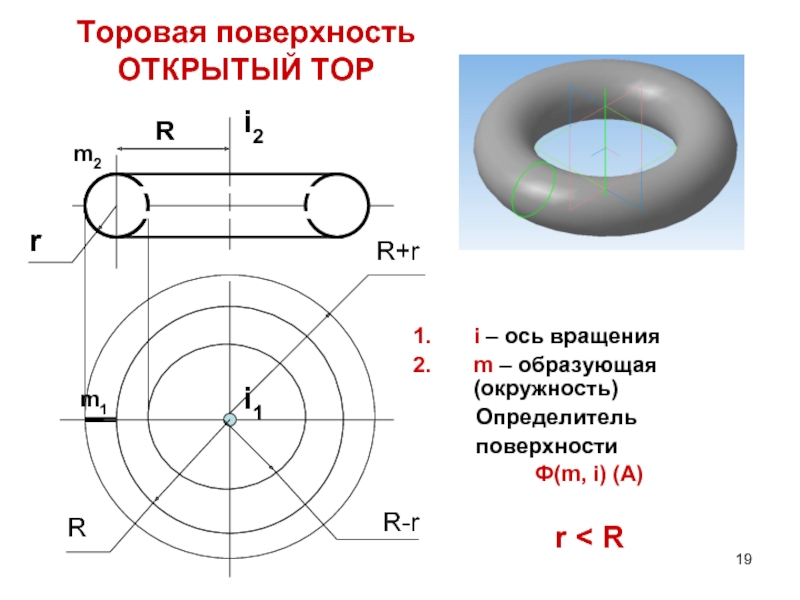
Торовая поверхность
ОТКРЫТЫЙ ТОР
i – ось вращения
m – образующая (окружность)
Определитель
поверхности
Ф(m, i) (A)
r < R
поверхности
Ф(m, i) (A)
r < R
i2
m2
m1
i1
r
R
R-r
R+r
R
Слайд 20
Торовая поверхность
ЗАКРЫТЫЙ ТОР
1. i – ось вращения
2. m – образующая
(окружность)
Определитель
поверхности
Ф(m, i) (A)
r = R
Определитель
поверхности
Ф(m, i) (A)
r = R
i2
m2
m1
i1
r
R
R+r
R
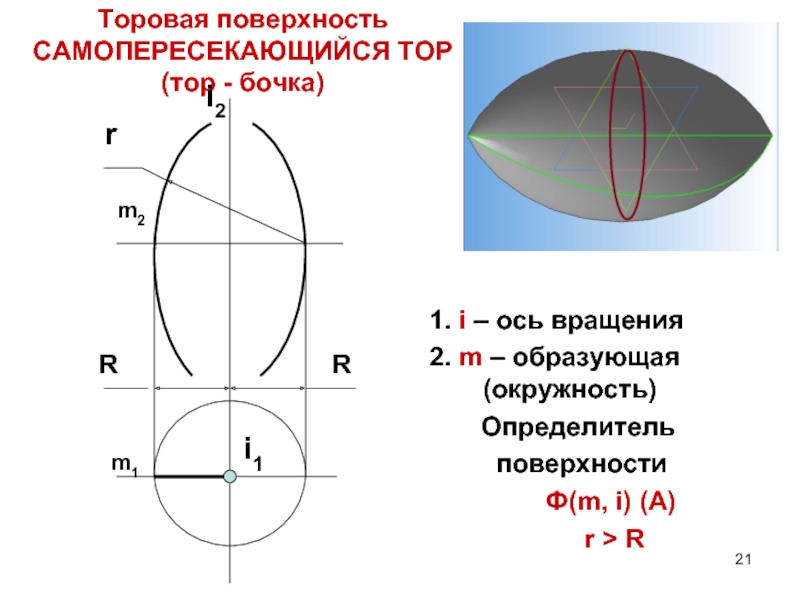
Слайд 21Торовая поверхность
САМОПЕРЕСЕКАЮЩИЙСЯ ТОР (тор - бочка)
1. i – ось вращения
2.
m – образующая (окружность)
Определитель
поверхности
Ф(m, i) (A)
r > R
Определитель
поверхности
Ф(m, i) (A)
r > R
R
r
i2
m2
m1
i1
R
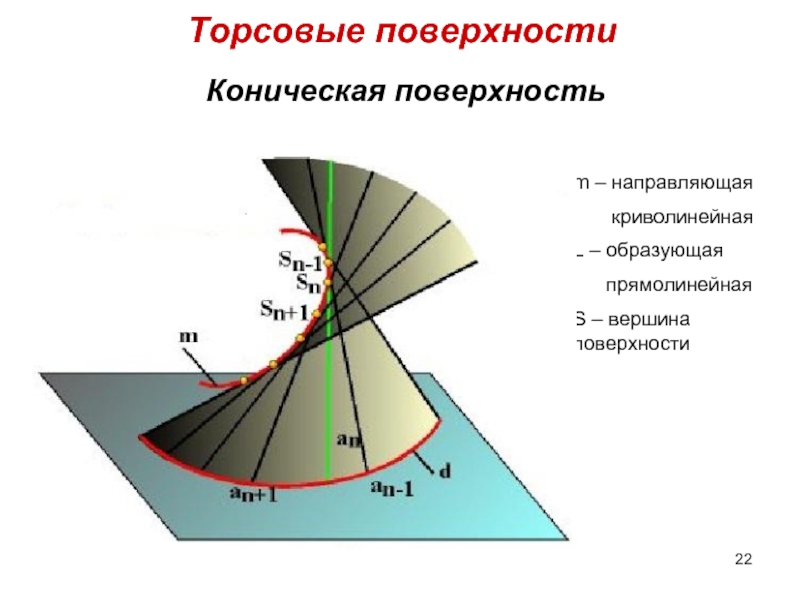
Слайд 22Коническая поверхность
Торсовые поверхности
X
m2
m1
S2
S1
l2
l1
m – направляющая
криволинейная
L – образующая
прямолинейная
S – вершина поверхности
S – вершина поверхности
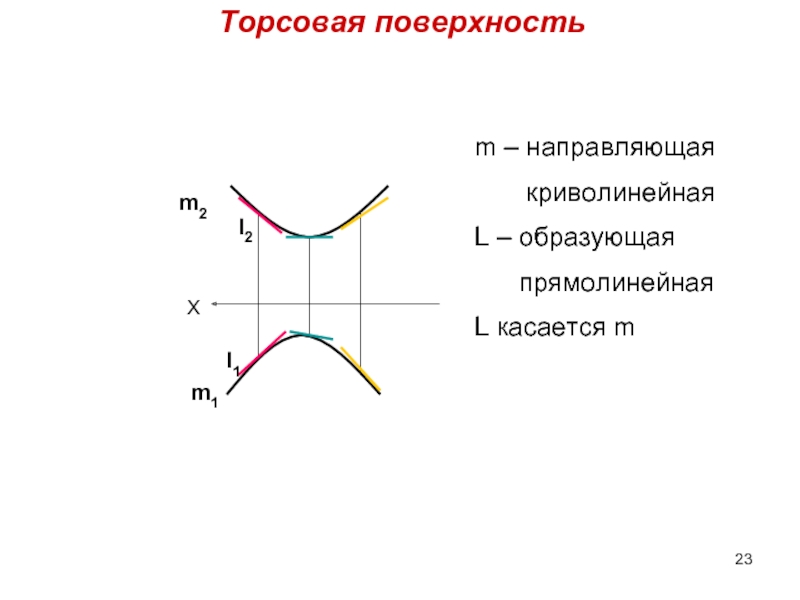
Слайд 23Торсовая поверхность
X
m2
m1
l2
l1
m – направляющая
криволинейная
L – образующая
прямолинейная
L касается m
L касается m
Слайд 24Поверхности Каталана
(с плоскостью параллелизма)
Цилиндроид
Коноид
Гиперболический параболоид (косая плоскость)
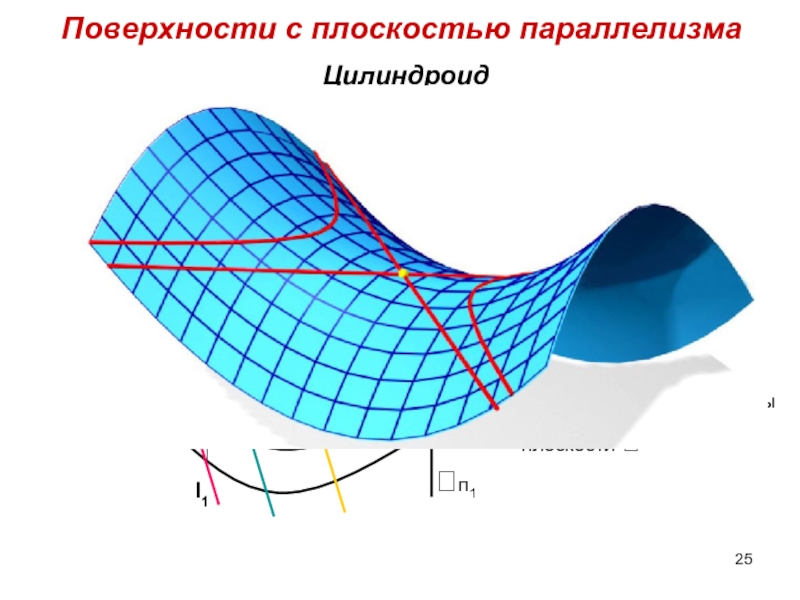
Слайд 25Поверхности c плоскостью параллелизма
Цилиндроид
X
m2
n2
m1
n1
l2
l1
m – направляющая
криволинейная
n – направляющая
криволинейная
- плоскость параллелизма
L – образующая
прямолинейная
Образующие параллельны
плоскости
- плоскость параллелизма
L – образующая
прямолинейная
Образующие параллельны
плоскости
п2
п1
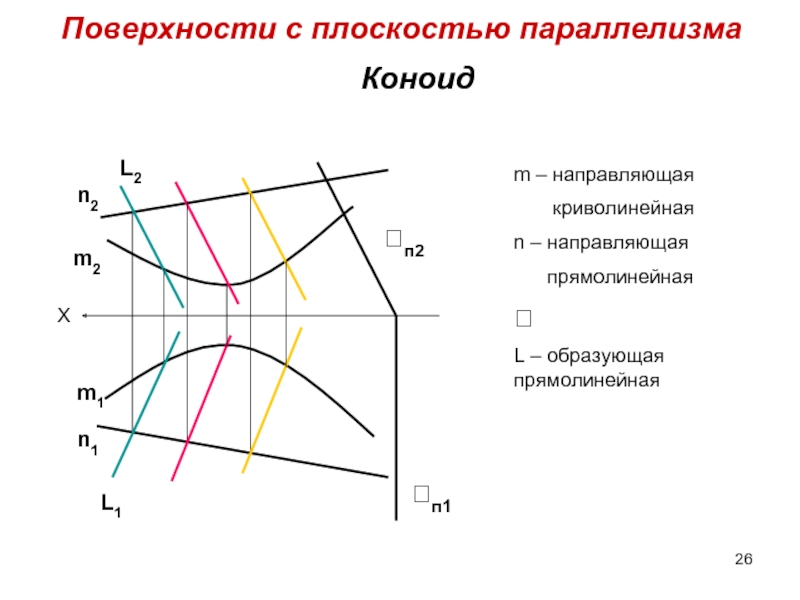
Слайд 26Коноид
Поверхности c плоскостью параллелизма
X
m2
m1
n2
n1
L2
L1
m – направляющая
криволинейная
n
– направляющая
прямолинейная
L – образующая прямолинейная
прямолинейная
L – образующая прямолинейная
п2
п1
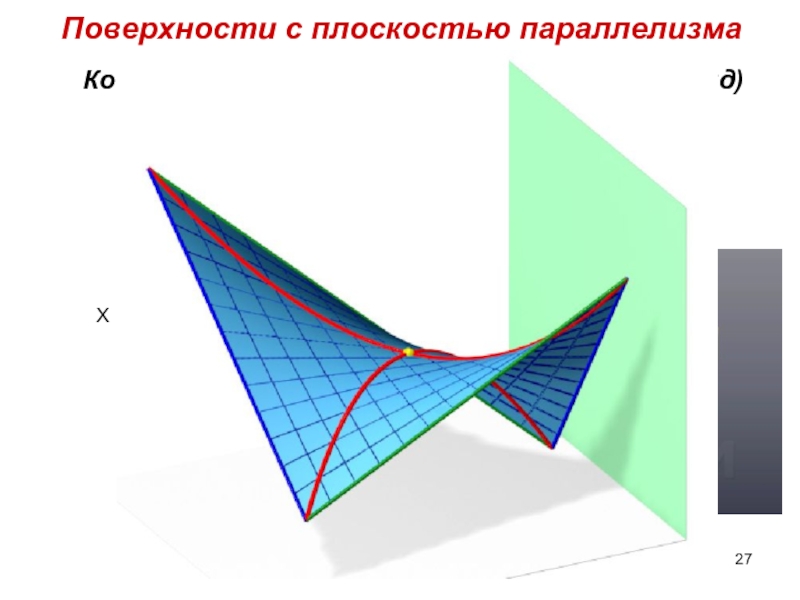
Слайд 27Косая плоскость (гиперболический параболоид)
Поверхности c плоскостью параллелизма
X
m2
m1
n2
n1
L2
L1
Слайд 28ВИНТОВЫЕ ПОВЕРХНОСТИ
Прямой и наклонный геликоид – частный случай поверхности коноида (прямолинейная
образующая, две направляющие – прямая линия и кривая линия)
Криволинейной направляющей является винтовая линия, цилиндрическая или коническая
Прямолинейная направляющая – ось винтовой линии
Лекция 4. Поверхности
Слайд 31Выводы по теме
Поверхностью называется множество положений линий, перемещающейся в пространстве по
определенному закону
Поверхности подразделяются на развертываемые и не развертываемые
Поверхность на эпюре задается графически ее очерком
Точка на поверхности принадлежит какой-либо линии поверхности
Поверхности подразделяются на развертываемые и не развертываемые
Поверхность на эпюре задается графически ее очерком
Точка на поверхности принадлежит какой-либо линии поверхности
Лекция 4. Поверхности
Слайд 32Рекомендованная литература
Бударин О. С. Начертательная геометрия. Краткий курс: учеб. пособие для
студентов вузов, обучающихся по направлениям в обл. техники и технологий / О. С. Бударин. - 2-е изд., испр. - Санкт-Петербург ; Москва ; Краснодар: Лань, 2009. - 368 с.
Королев Ю. И. Начертательная геометрия: учеб. для вузов инженер.-техн. специальностей / Ю. И. Королев. - 2-е изд. - Москва ; Санкт-Петербург ; Нижний Новгород [и др.]: Питер, 2010. - 256 с.
Чекмарев А. А. Начертательная геометрия и черчение: учеб. для студентов вузов, обучающихся по техн. специальностям / А. А. Чекмарев. - 3-е изд., перераб. и доп. - Москва: Юрайт, 2011. - 471 с.
Королев Ю. И. Начертательная геометрия: учеб. для вузов инженер.-техн. специальностей / Ю. И. Королев. - 2-е изд. - Москва ; Санкт-Петербург ; Нижний Новгород [и др.]: Питер, 2010. - 256 с.
Чекмарев А. А. Начертательная геометрия и черчение: учеб. для студентов вузов, обучающихся по техн. специальностям / А. А. Чекмарев. - 3-е изд., перераб. и доп. - Москва: Юрайт, 2011. - 471 с.
Лекция 4. Поверхности
