- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
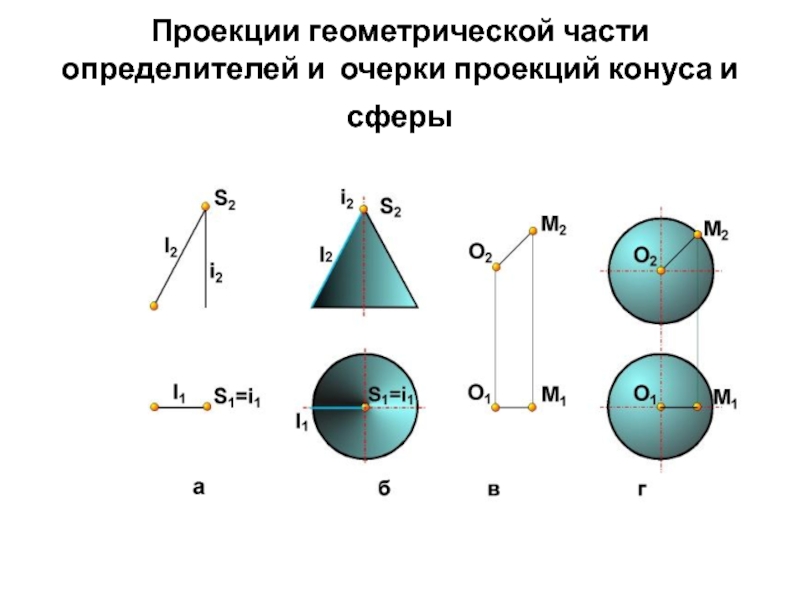
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Поверхности. Образование и задание на чертеже презентация
Содержание
- 1. Поверхности. Образование и задание на чертеже
- 2. Поверхности.
- 3. Классификация поверхностей Поверхности
- 4. ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ В начертательной геометрии
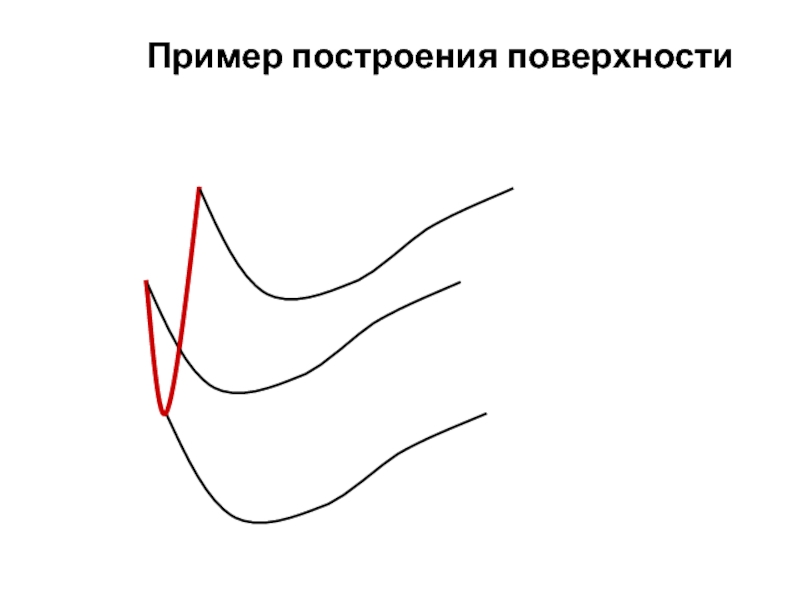
- 5. Пример построения поверхности
- 7. Определения поверхности Поверхностью называется:
- 8. Задание поверхности Для получения наглядного изображения поверхностиДля
- 9. Задание кинематической кривой поверхности На чертеже
- 10. i
- 11. Примеры образования поверхностей Примером такого способа образования
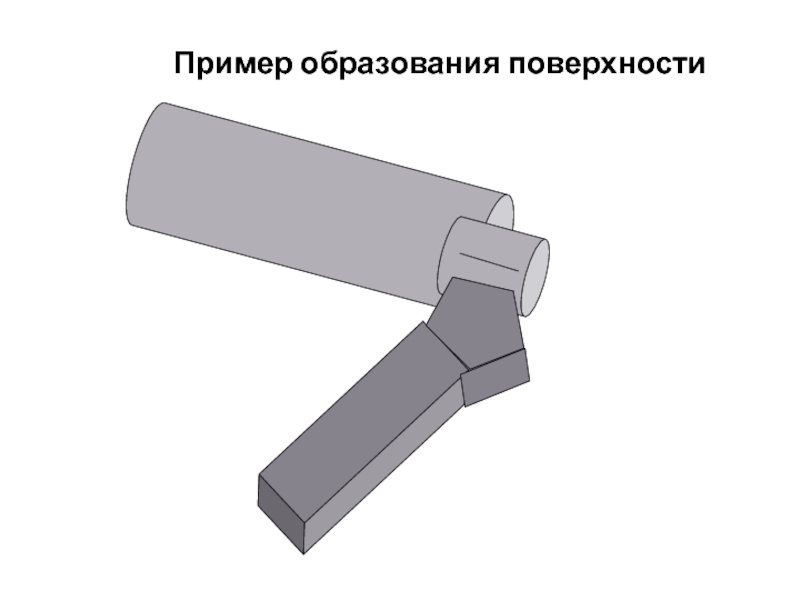
- 13. Пример образования поверхности
- 14. Способы задания кривых поверхностей Кривые поверхности широко
- 15. Аналитический способ задания поверхности Составлением уравнений
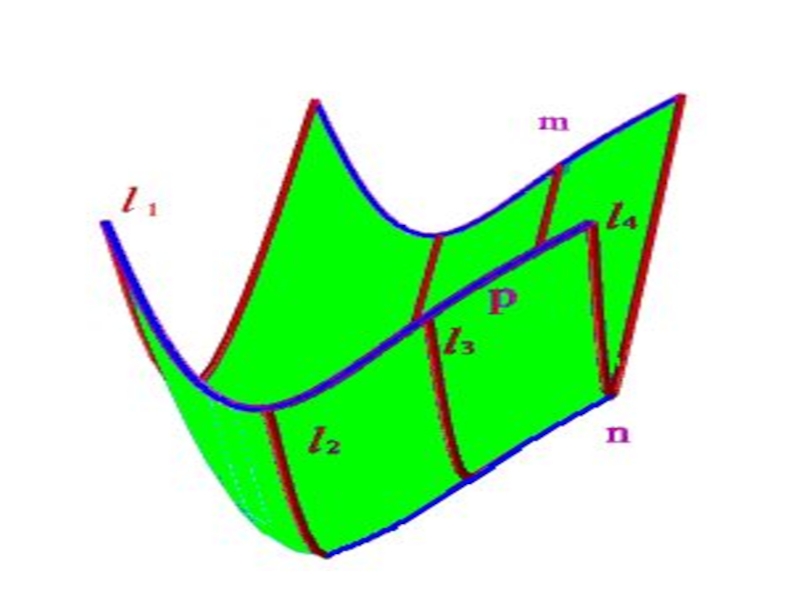
- 17. Каркас поверхности Каркасом поверхности принято называть
- 18. Эта зависимость характеризуется некоторой изменяющейся величиной, которая
- 19. Пример дискретного каркаса
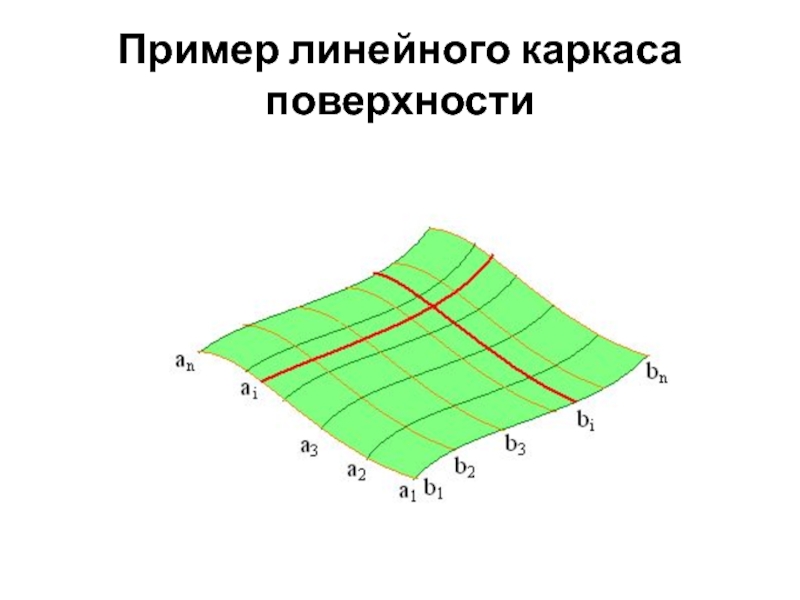
- 20. Пример линейного каркаса поверхности
- 21. Каркас Упорядоченное множество точек или линий, принадлежащих
- 22. Определитель поверхности Кинематический способ образования поверхности
- 23. Состав определителя 1. Геометрическая часть - совокупность
- 24. Выбор определителя поверхности Определитель поверхности выявляется путем
- 25. Определитель поверхности Совокупность параметров, однозначно определяющих данную
- 26. Поверхность на комплексном чертеже Поверхность считается заданной
- 27. Примеры определителя поверхностей Через три
- 28. Пример определителя плоскости А2
- 29. Определитель цилиндрической поверхности Цилиндрическая поверхность
- 30. Изображение определителя конической поверхности Коническая поверхность
- 31. Проекции геометрической части определителей и очерки проекций конуса и сферы
- 32. Поверхности на комплексном чертеже могут быть заданы:
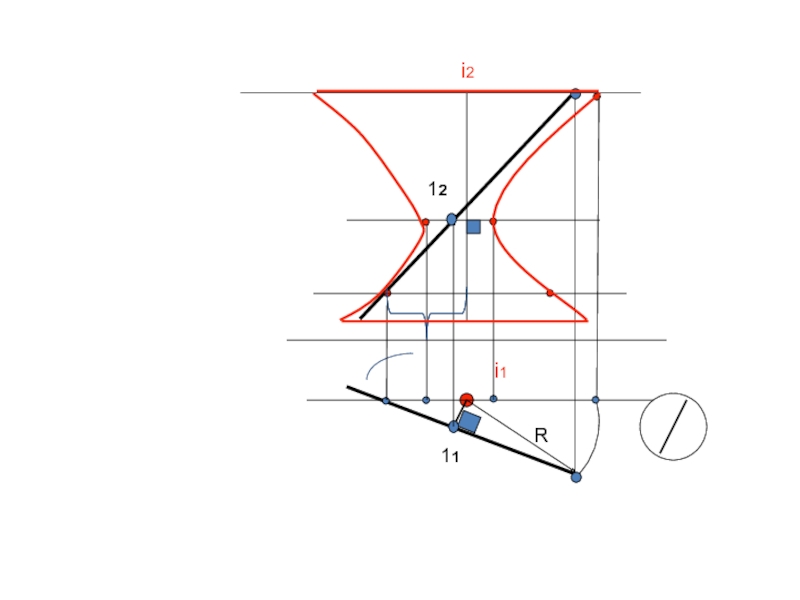
- 33. i2 i1 11
- 34. Виды кривых поверхностей Кривые поверхности разделяются на
- 35. Закономерные поверхности Закономерные поверхности, в зависимости от
- 36. Примеры кривых поверхностей Примерами кривых поверхностей второго
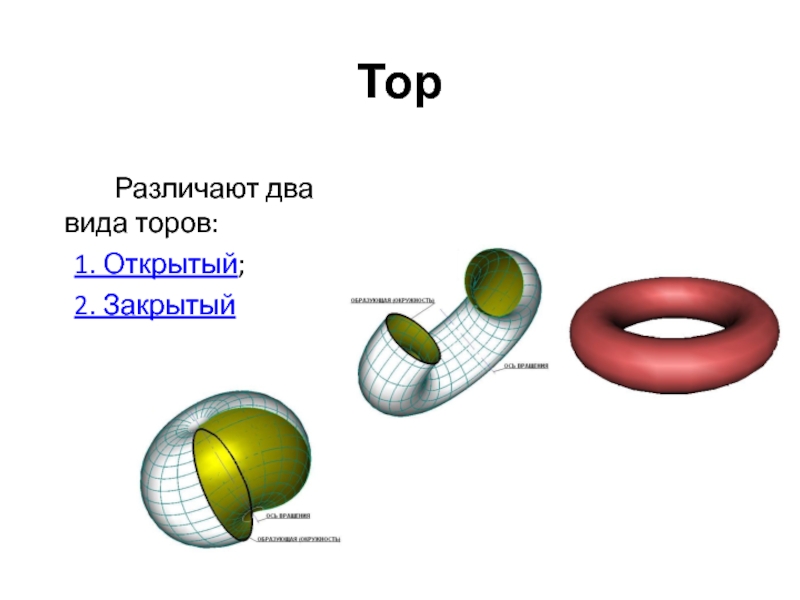
- 37. Тор Различают два вида торов: 1. Открытый; 2. Закрытый
- 38. Тор открытый Если окружность радиусом
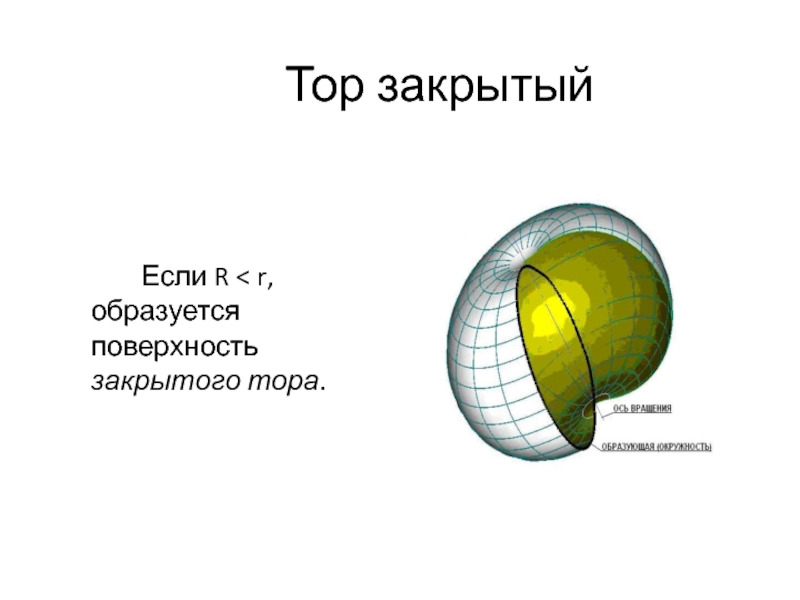
- 39. Тор закрытый Если R < r, образуется поверхность закрытого тора.
- 40. Кинематические кривые поверхности Наибольшее применение в технике
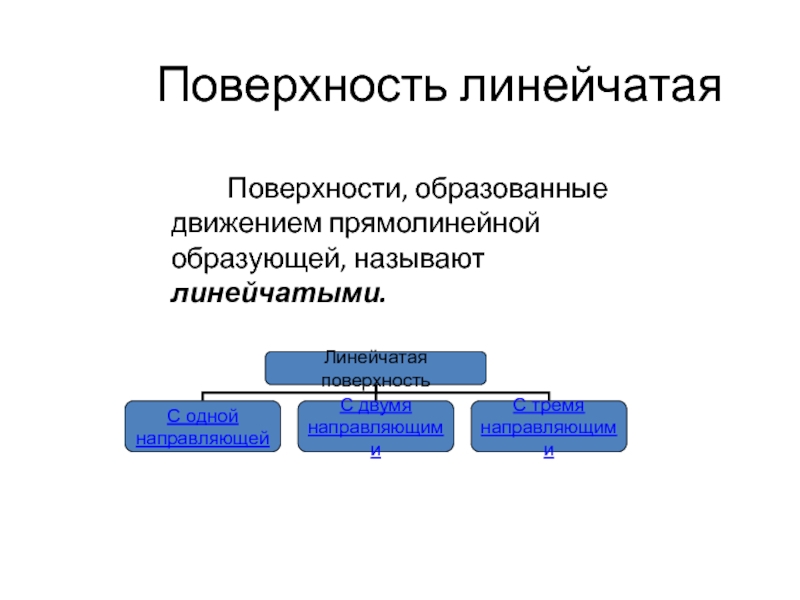
- 41. Поверхность линейчатая Поверхности, образованные движением прямолинейной образующей, называют линейчатыми.
- 42. Поверхность линейчатая с одной направляющей Примерами линейчатых
- 43. Поверхность линейчатая с двумя направляющими Примерами линейчатых
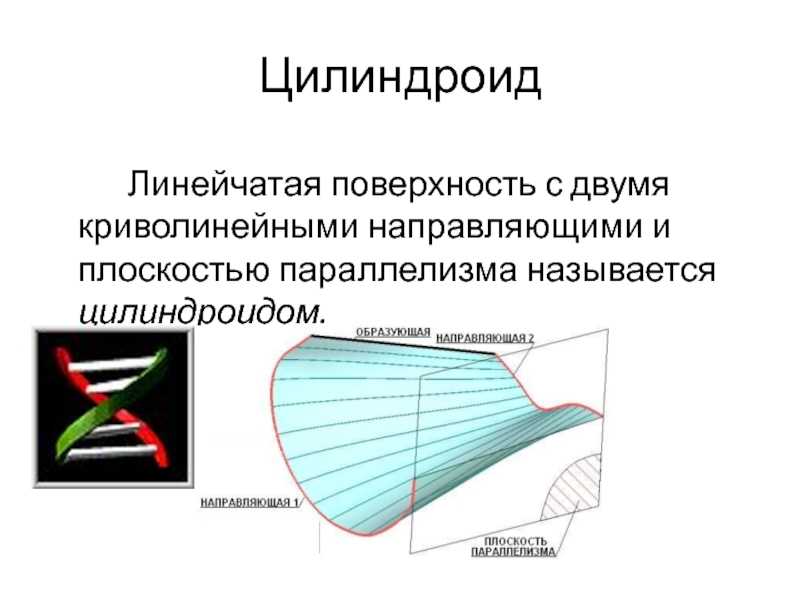
- 44. Цилиндроид Линейчатая поверхность с двумя криволинейными направляющими и плоскостью параллелизма называется цилиндроидом.
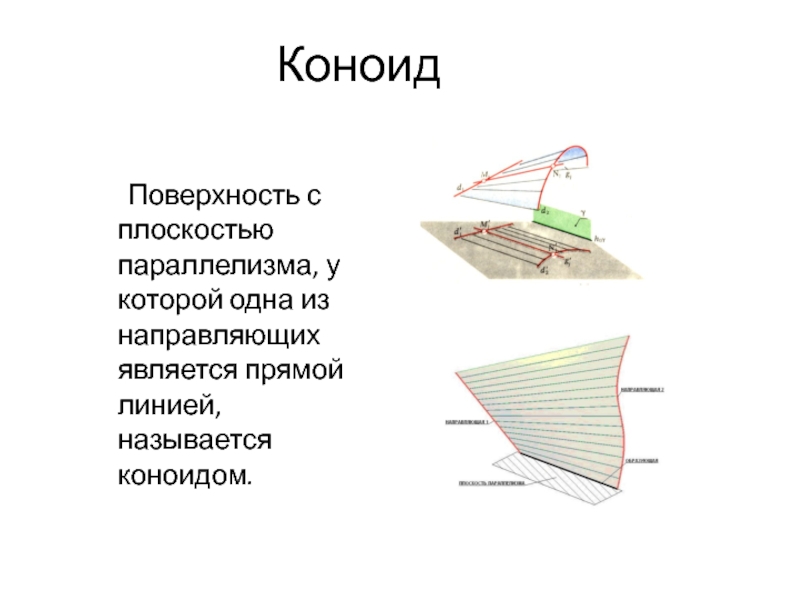
- 45. Коноид Поверхность с плоскостью параллелизма, у которой
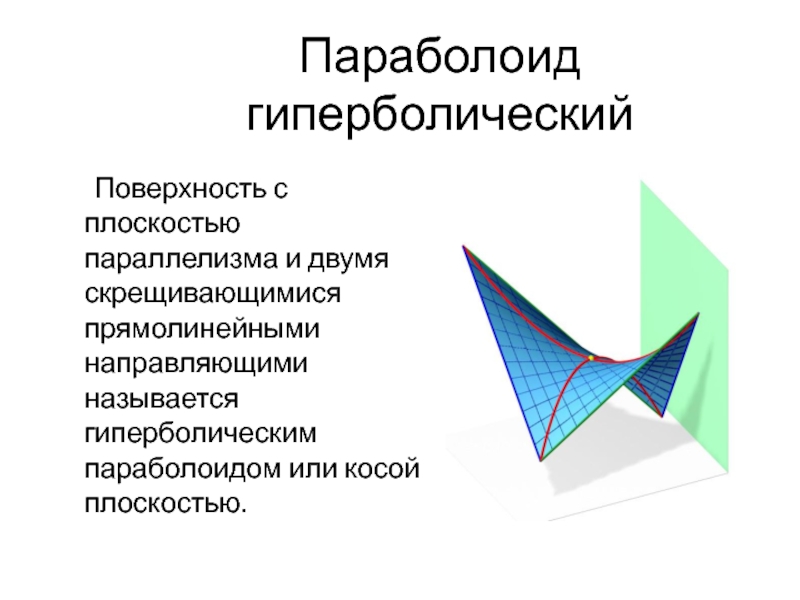
- 46. Параболоид гиперболический Поверхность с плоскостью параллелизма и
- 47. ЛИНЕЙЧАТЫЕ ПОВЕРХНОСТИ Как уже отмечалось, поверхность
- 48. Виды линейчатых поверхностей Линейчатые поверхности разделяются на
- 49. Поверхности с ребром возврата (торсы) Все нелинейчатые
- 50. d m a
- 51. Поверхности развертывающиеся Поверхностью с ребром возврата (торсом)
- 52. Пример конической поверхности Существует только три вида
- 53. Пример цилиндрической поверхности Необходимо отметить, что у
- 54. НЕРАЗВЕРТЫВАЮЩИЕСЯ (КОСЫЕ) ЛИНЕЙЧАТЫЕ ПОВЕРХНОСТИ. Неразвертывающиеся линейчатые поверхности
- 55. Косые поверхности Разновидностями косых поверхностей являются линейчатые
- 56. Поверхность Каталана Поверхности с двумя направляющими и
- 57. Поверхность линейчатая с тремя направляющими Примерами линейчатых
- 58. Цилиндр косой Линейчатая поверхность с тремя криволинейными
- 59. Поверхность общего вида Линейчатая поверхность с
- 60. Цилиндроид дважды косой Если одна из направляющих -прямая, поверхность называют дважды косым цилиндроидом.
- 61. Коноид дважды косой Если две направляющие прямые
- 62. Поверхность вращения Поверхность вращения образована вращением
- 63. Поверхности вращения Поверхности вращения – это поверхности
- 64. Так создается каркас поверхности, состоящей из множества
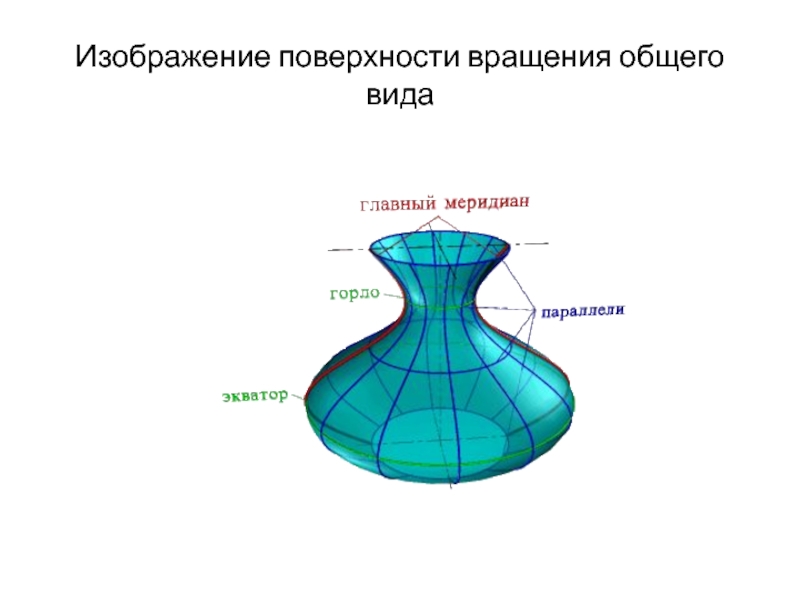
- 65. Изображение поверхности вращения общего вида
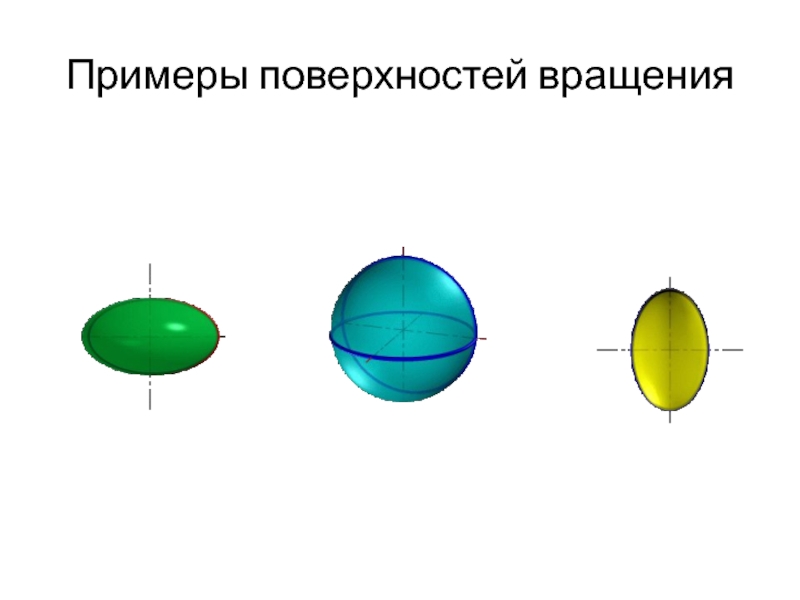
- 66. Примеры поверхностей вращения
- 67. Примеры косой плоскости
- 69. Поверхность Поверхностью называется совокупность всех последовательных положений
- 70. Поверхности разделяют: По
- 71. Поверхности на комплексном чертеже могут быть заданы:
- 72. КЛАССИФИКАЦИЯ ПОВЕРХНОСТЕЙ В зависимости
Слайд 2
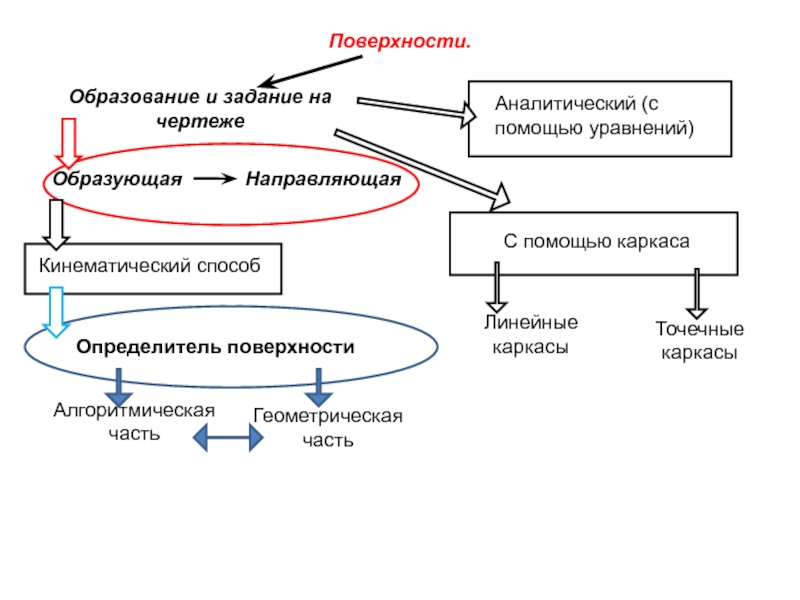
Поверхности.
Образование и задание на чертеже
Образующая
Направляющая
Кинематический способ
С помощью каркаса
Аналитический (с
Определитель поверхности
Алгоритмическая часть
Геометрическая часть
Точечные каркасы
Линейные каркасы
Слайд 4ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ
В начертательной геометрии фигуры задаются графически, поэтому целесообразно
Слайд 7Определения поверхности
Поверхностью называется:
совокупность всех последовательных положений линий, непрерывно
непрерывное двупараметрическое множество точек.
Слайд 8Задание поверхности
Для получения наглядного изображения поверхностиДля получения наглядного изображения поверхности на
Слайд 9Задание кинематической кривой поверхности
На чертеже кинематическая кривая поверхность задается при
Слайд 11Примеры образования поверхностей
Примером такого способа образования могут служить все технологические процессы
Режущие кромки являются неотъемлемой частью исполнительных механизмов многих строительных и дорожных машин, применяемых не только для разработки и перемещения грунта (бульдозеры, грейдеры и т. п.), но и рытье траншей, котлованов, проходка траншей, профилирование откосов и многое другое.
Слайд 14Способы задания кривых поверхностей
Кривые поверхности широко применяются в различных областях науки
1. Аналитический - при помощи уравнений;
2. При помощи каркаса;
3. Кинематический, т. е. перемещением линий в пространстве.
Слайд 15 Аналитический способ задания поверхности
Составлением уравнений поверхностей занимается аналитическая геометрия; она
Слайд 17Каркас поверхности
Каркасом поверхности принято называть упорядоченное множество точек или линий,
Линейным каркасом называется множество таких линий, которые имеют единый закон образования и связаны между собой определенной зависимостью. Условия связи между линиями каркаса называются зависимостью каркаса.
Слайд 18Эта зависимость характеризуется некоторой изменяющейся величиной, которая называется параметром каркаса.
Если
Слайд 21Каркас
Упорядоченное множество точек или линий, принадлежащих поверхности, называется каркасом.
В зависимости от
Слайд 22Определитель поверхности
Кинематический способ образования поверхности можно представить как множество положений
Этот способ дает возможность сформулировать понятие определителя поверхности. Под этим понятием обычно подразумевают необходимую и достаточную совокупность геометрических фигур и кинематических связей между ними, которые однозначно определяют поверхность.
Слайд 23Состав определителя
1. Геометрическая часть - совокупность геометрических фигур, с помощью которых
2. Алгоритмическая часть - алгоритм формирования поверхности при помощи фигур, входящих в геометрическую часть определителя.
Чтобы найти определитель поверхности, следует исходить из кинематического способа образования поверхности.
Слайд 24Выбор определителя поверхности
Определитель поверхности выявляется путем анализа способов образования поверхности или
Слайд 25Определитель поверхности
Совокупность параметров, однозначно определяющих данную поверхность, называют определителем.
Алгоритмическая часть определителя
Алгоритмическая часть определителя задаётся в виде описания, например словом «сфера» или «вращение».
Геометрическая часть определителя содержит форму образующих и направляющих.
Геометрическая часть определителя может задаваться в виде числа, например R50.
Слайд 26Поверхность на комплексном чертеже
Поверхность считается заданной на комплексном чертеже, если относительно
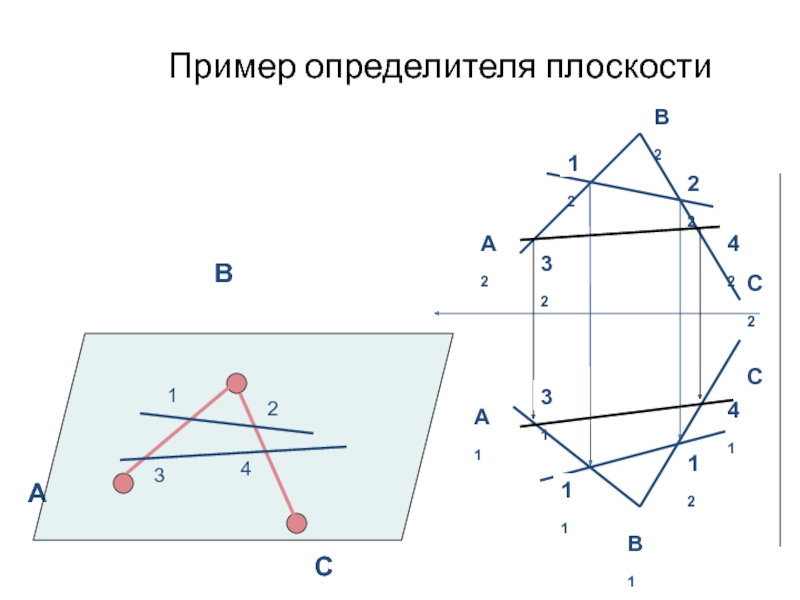
Слайд 27Примеры определителя поверхностей
Через три точки А, В, С, не
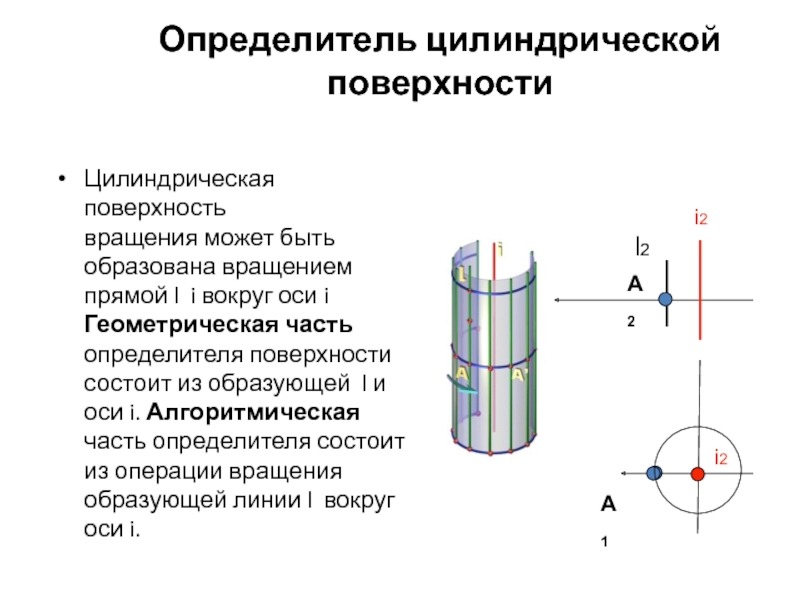
Слайд 29Определитель цилиндрической поверхности
Цилиндрическая поверхность
l2
i2
А2
А1
i2
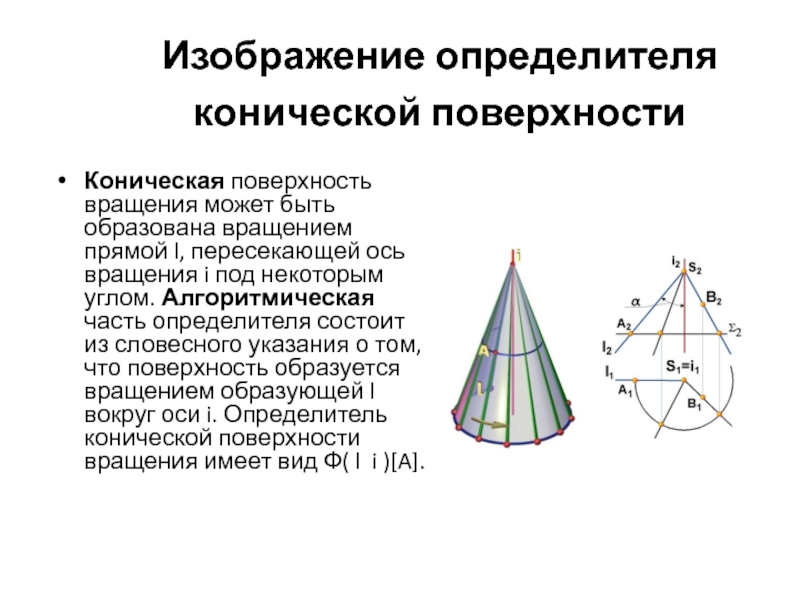
Слайд 30Изображение определителя конической поверхности
Коническая поверхность вращения может быть образована вращением
Слайд 32Поверхности на комплексном чертеже могут быть заданы:
Проекциями направляющих и способом
Семейством линий, принадлежащих поверхности - каркасный способ задания поверхности.
Очерком поверхности, т.е. линиями, ограничивающими на комплексном чертеже область существования проекций.
Слайд 34Виды кривых поверхностей
Кривые поверхности разделяются на линейчатые и нелинейчатые, закономерные и
Если поверхность может быть задана каким-либо уравнением, она называется закономерной, в противном случае − незакономерной, или графической (задается только чертежом).
Слайд 35Закономерные поверхности
Закономерные поверхности, в зависимости от вида уравнения, разделяются на алгебраические
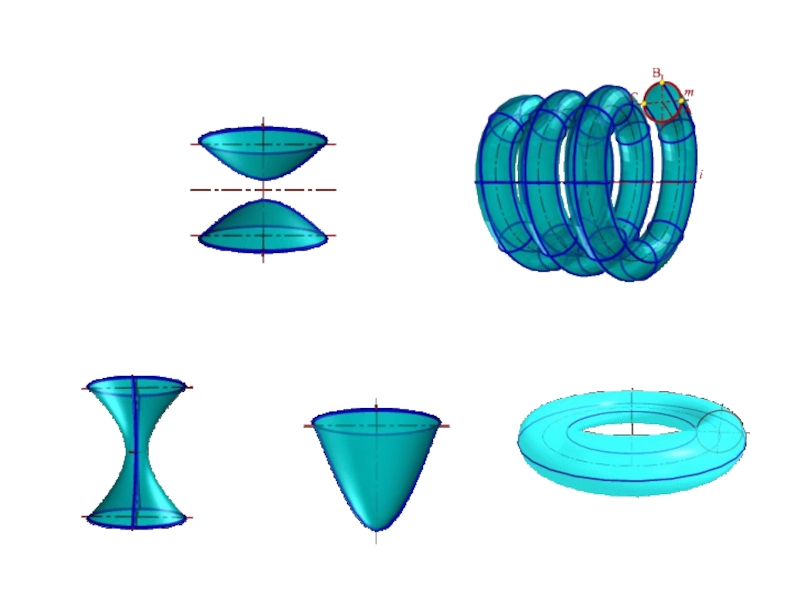
Слайд 36Примеры кривых поверхностей
Примерами кривых поверхностей второго порядка могут служить поверхности, образованные
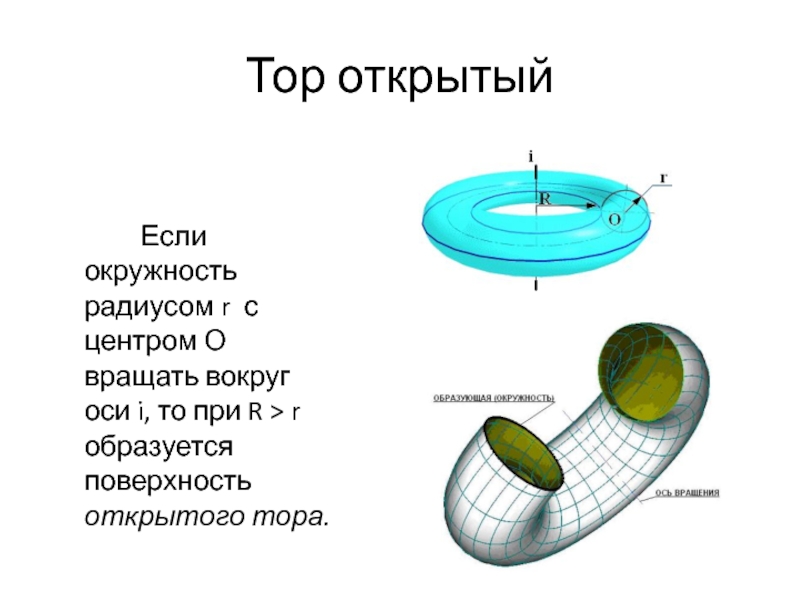
Слайд 38Тор открытый
Если окружность радиусом r с центром О вращать вокруг
Слайд 40Кинематические кривые поверхности
Наибольшее применение в технике получили кинематические кривые поверхности с
1. Линейчатые поверхности:
а) развертывающиеся; б) неразвертывающиеся; в) винтовые.
2. Поверхности вращения.
Слайд 41Поверхность линейчатая
Поверхности, образованные движением прямолинейной образующей, называют линейчатыми.
Слайд 42Поверхность линейчатая с одной направляющей
Примерами линейчатых поверхностей с одной направляющей могут
- цилиндрическая поверхность;
- коническая поверхность;
- различные виды торсов и т.д.
Слайд 43Поверхность линейчатая с двумя направляющими
Примерами линейчатых поверхностей с двумя направляющими могут
- поверхность цилиндроида;
- поверхность коноида;
- гиперболический параболоид и пр.
Слайд 44Цилиндроид
Линейчатая поверхность с двумя криволинейными направляющими и плоскостью параллелизма называется цилиндроидом.
Слайд 45Коноид
Поверхность с плоскостью параллелизма, у которой одна из направляющих является прямой
Слайд 46Параболоид гиперболический
Поверхность с плоскостью параллелизма и двумя скрещивающимися прямолинейными направляющими называется
Слайд 47ЛИНЕЙЧАТЫЕ ПОВЕРХНОСТИ
Как уже отмечалось, поверхность называется линейчатой, если она может
Слайд 48Виды линейчатых поверхностей
Линейчатые поверхности разделяются на два вида:
1) развертывающиеся поверхности;
2)
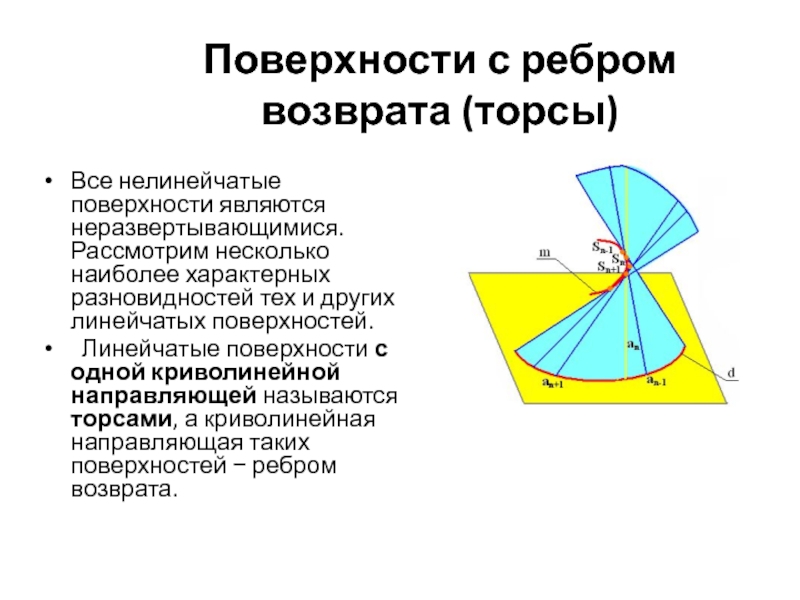
Слайд 49Поверхности с ребром возврата (торсы)
Все нелинейчатые поверхности являются неразвертывающимися. Рассмотрим несколько
Линейчатые поверхности с одной криволинейной направляющей называются торсами, а криволинейная направляющая таких поверхностей − ребром возврата.
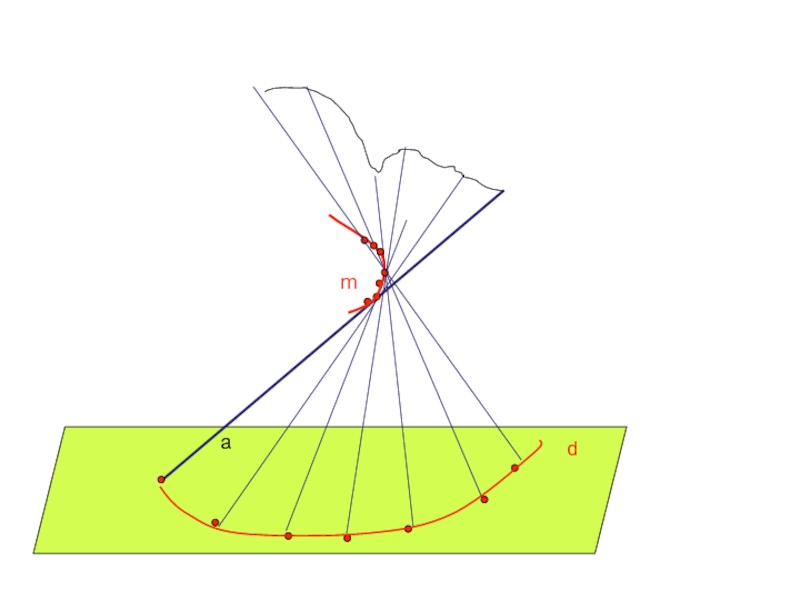
Слайд 51Поверхности развертывающиеся
Поверхностью с ребром возврата (торсом) называют поверхность, описываемую движением прямой
Поверхность называется развертывающейся, если она путем изгибания может быть совмещена с плоскостью без образования складок и разрывов. Очевидно, что все многогранные поверхности являются развертывающимися. Из кривых поверхностей этим свойством обладают только те линейчатые поверхности, которые имеют ребро возврата.
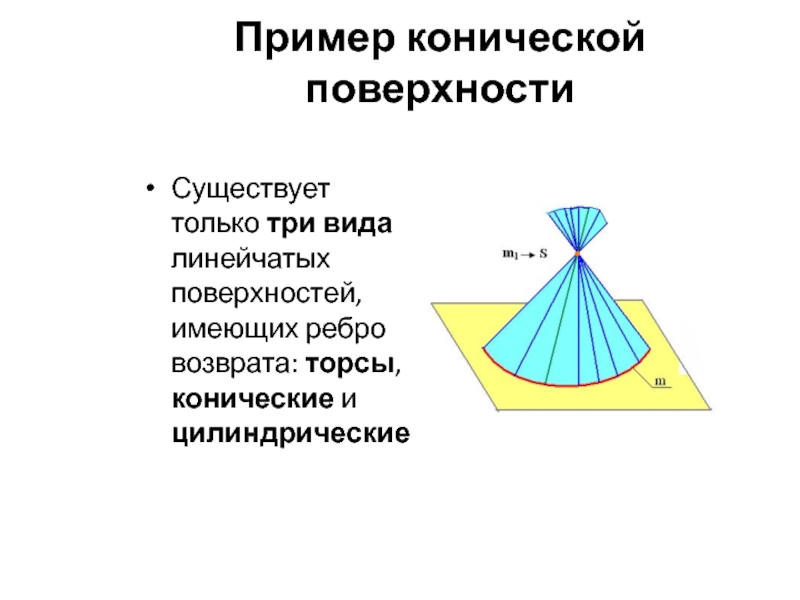
Слайд 52Пример конической поверхности
Существует только три вида линейчатых поверхностей, имеющих ребро возврата:
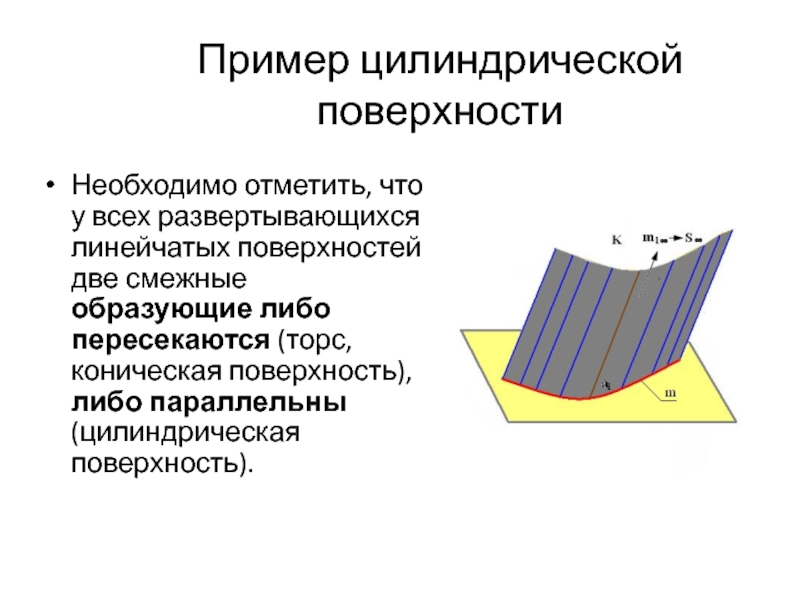
Слайд 53Пример цилиндрической поверхности
Необходимо отметить, что у всех развертывающихся линейчатых поверхностей две
Слайд 54НЕРАЗВЕРТЫВАЮЩИЕСЯ (КОСЫЕ) ЛИНЕЙЧАТЫЕ ПОВЕРХНОСТИ.
Неразвертывающиеся линейчатые поверхности в общем случае образуются движением
Слайд 55Косые поверхности
Разновидностями косых поверхностей являются линейчатые поверхности с направляющей плоскостью и
Слайд 56Поверхность Каталана
Поверхности с двумя направляющими и плоскостью параллелизма называют поверхностями Каталана
Слайд 57Поверхность линейчатая с тремя направляющими
Примерами линейчатых поверхностей с тремя направляющими могут
- косой цилиндр;
- дважды косой цилиндроид;
- дважды косой коноид и т. д.
Слайд 58Цилиндр косой
Линейчатая поверхность с тремя криволинейными направляющими называется поверхностью общего вида,
Слайд 59Поверхность общего вида
Линейчатая поверхность с тремя криволинейными направляющими называется поверхностью общего
Слайд 60Цилиндроид дважды косой
Если одна из направляющих -прямая, поверхность называют дважды косым
Слайд 61Коноид дважды косой
Если две направляющие прямые и одна кривая, то поверхность
Слайд 62Поверхность вращения
Поверхность вращения образована вращением образующей вокруг неподвижной прямой —
Например, представителями данного класса поверхностей являются геометрические фигуры:
- прямой круговой цилиндр;
- прямой круговой конус;
- однополосный гиперболоид вращения;
- сфера;
- открытый тор и т. д .
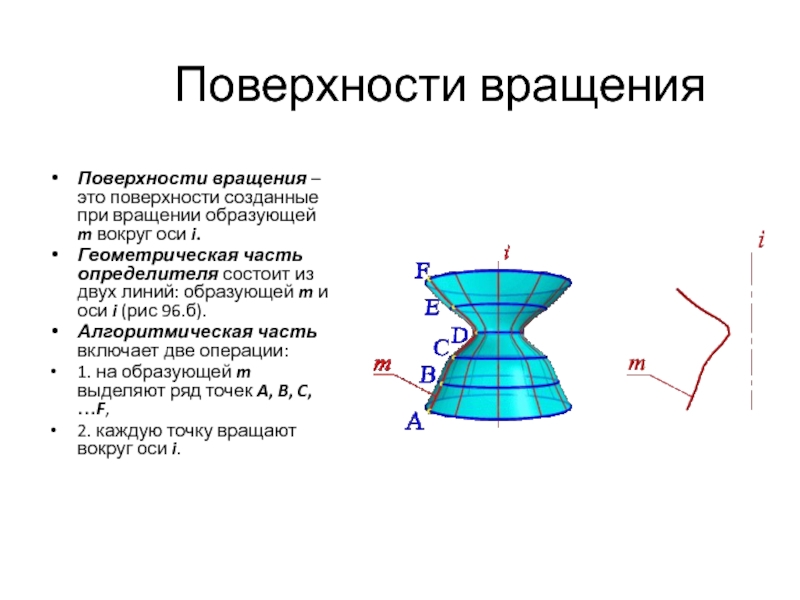
Слайд 63Поверхности вращения
Поверхности вращения – это поверхности созданные при вращении образующей m
Геометрическая часть определителя состоит из двух линий: образующей m и оси i (рис 96.б).
Алгоритмическая часть включает две операции:
1. на образующей m выделяют ряд точек A, B, C, …F,
2. каждую точку вращают вокруг оси i.
Слайд 64Так создается каркас поверхности, состоящей из множества окружностей (рис.97), плоскости которых
Из закона образования поверхности вращения вытекают два основных свойства:
1. Плоскость перпендикулярная оси вращения, пересекает поверхность по окружности – параллели.
2. Плоскость, проходящая через ось вращения, пересекает поверхность по двум
симметричным относительно оси линиям – меридианам.
Плоскость, проходящая через ось параллельно фронтальной плоскости проекций называется плоскостью главного меридиана, а линия, полученная в сечении, – главным меридианом.
Слайд 69Поверхность
Поверхностью называется совокупность всех последовательных положений линий, непрерывно перемещающихся в пространстве.
Следовательно,
Линия, образующая поверхность, называется образующей.
Линия, по которой перемещается образующая, называется направляющей.
Образующие могут быть постоянными и изменяться.
Слайд 70 Поверхности разделяют:
По закону образования - на закономерные
По признаку развёртывания в плоскость - развёртывающиеся и неразвёртывающиеся.
По форме образующей: - с прямолинейными образующими - линейчатые поверхности; - с криволинейной образующей - кривые поверхности.
По способу перемещения образующей: - с поступательным движением образующей; - с вращательным движением образующей - поверхности вращения; - с движением образующей по винтовой линии - винтовые поверхности.
Слайд 71Поверхности на комплексном чертеже могут быть заданы:
Проекциями направляющих и способом
Семейством линий, принадлежащих поверхности - каркасный способ задания поверхности.
Очерком поверхности, т.е. линиями, ограничивающими на комплексном чертеже область существования проекций.
Слайд 72КЛАССИФИКАЦИЯ ПОВЕРХНОСТЕЙ
В зависимости от формы образующей и закона ее перемещения в
Линейчатые поверхности - поверхности, которые могут быть образованы с помощью прямой линии.
Нелинейчатые поверхности - поверхности, которые могут быть образованы только с помощью кривой линии.
Развертывающиеся поверхности - поверхности, которые после разреза их по образующей могут быть совмещены с плоскостью без наличия разрывов и складок.
Неразвертывающиеся поверхности - поверхности, которые не могут быть совмещены с плоскостью без наличия разрывов и складок.
Поверхности с постоянной образующей - поверхности, образующая которых не изменяет своей формы в процессе образования поверхности.
Поверхности с переменной образующей - поверхности, образующая которых изменяется в процессе образования поверхности.