- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Поверхности (лекция 4) презентация
Содержание
- 1. Поверхности (лекция 4)
- 2. Поверхности
- 3. Примеры современных архитектурных форм
- 4. Поверхность – непрерывное двумерное множество точек. Измерения
- 5. Поверхность рассматривается как непрерывное множество
- 6. Способы задания поверхности
- 7. Определитель поверхности Это совокупность независимых
- 8. Пример Ф { g(d1,d2,Σ)(g∩d1, g∩d2, gIIΣ) }
- 9. Очерк поверхности gΩi II s Ω ∩
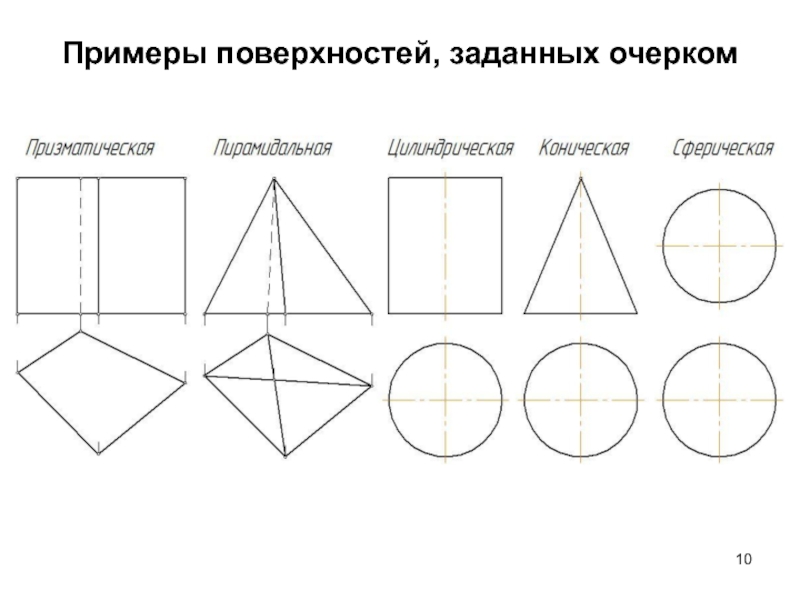
- 10. Примеры поверхностей, заданных очерком
- 11. Каркас поверхности Каркас поверхности – это множество
- 13. Геометрическая поверхность Графическая поверхность
- 14. Геометрические поверхности
- 15. Линейчатые поверхности Образующая поверхности – прямая линия
- 16. С тремя направляющими Поверхность косого клина Поверхность косого перехода Ф{g(d1,d2,d3)(g∩d1, g∩d2, g∩d3)}
- 17. Ф{g(d1,d2,α)(g∩d1, g∩d2,gIIα)} Ф{g(d1,d2,α)(g∩d1, g∩d2,
- 18. Линейчатые поверхности с одной направляющей Торсы
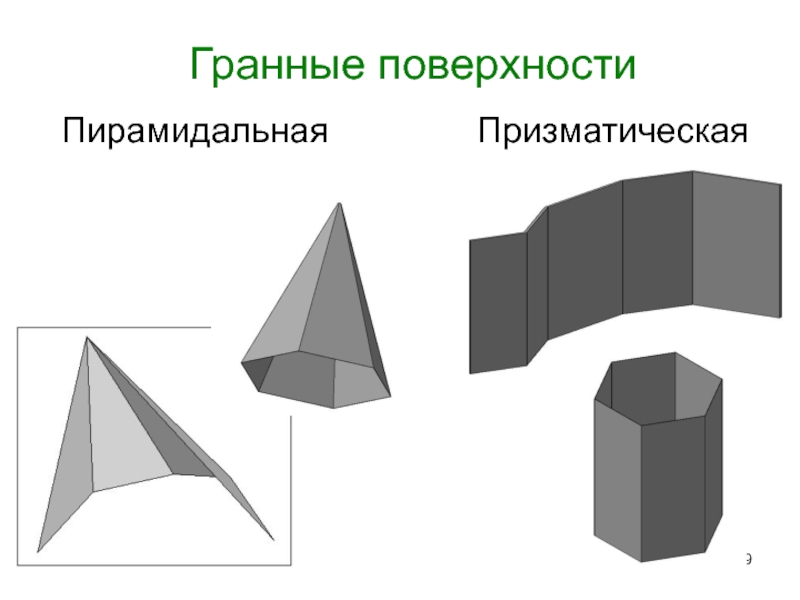
- 19. Гранные поверхности Призматическая Пирамидальная
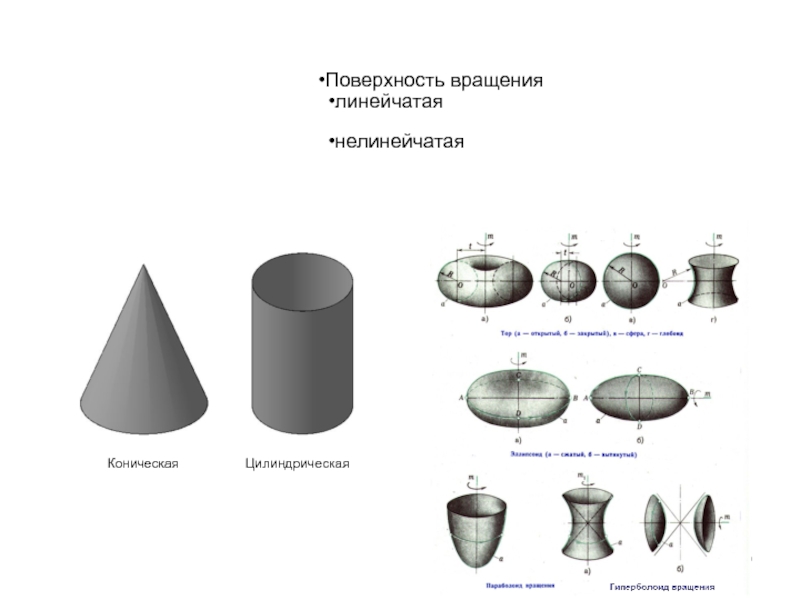
- 20. Поверхность вращения линейчатая нелинейчатая Коническая Цилиндрическая
- 22. Винтовые поверхности Прямой геликоид, Винтовой коноид
- 23. Винтовые поверхности
- 24. Ф{g(d1,d2)(g∩d1,g∩d2,(g^d2)=const)}
- 25. Поверхности параллельного переноса
- 27. Обобщенные позиционные задачи
- 28. Точка на поверхности
- 29. Точка принадлежит поверхности, если она
- 30. Точка на линейчатой поверхности Так как образующей
- 31. Точка на поверхности вращения Линия l, которой
- 32. Линия на поверхности
- 33. Линия принадлежит поверхности, если все множество ее
- 34. Построение произвольной линии на поверхности В
- 35. Пересечение поверхности плоскостью
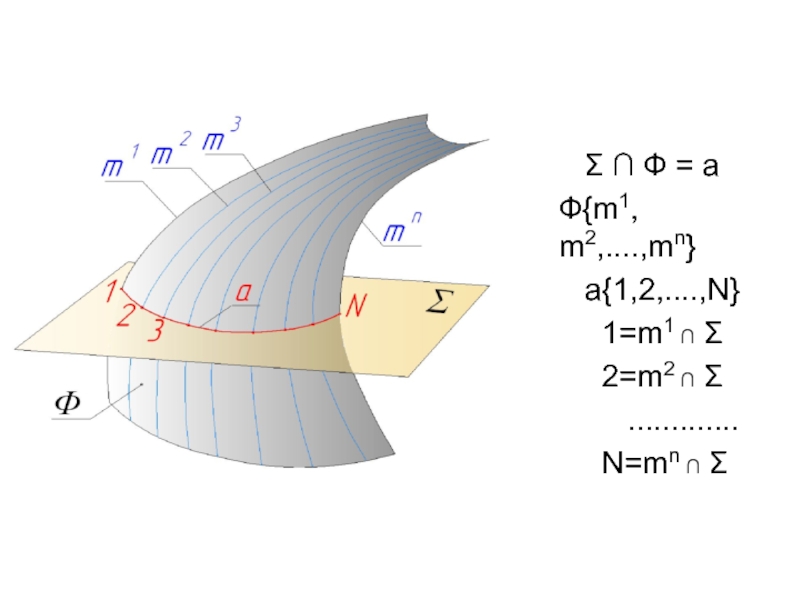
- 36. Σ ∩ Ф = a
- 37. Линию пересечения поверхности плоскостью следует рассматривать как
- 38. Из всего множества точек линии пересечения должны
- 39. Пересечение гранной поверхности плоскостью
- 40. При пересечении гранной поверхности плоскостью линия пересечения
- 41. Ф – трехгранная пирамида. Р – секущая
- 42. m=Ф∩Р; m⊂P
- 43. Пересечение конической поверхности плоскостью
- 44. При пересечении прямой круговой конической поверхности плоскостью
- 45. Ф – прямая круговая коническая поверхность. Т
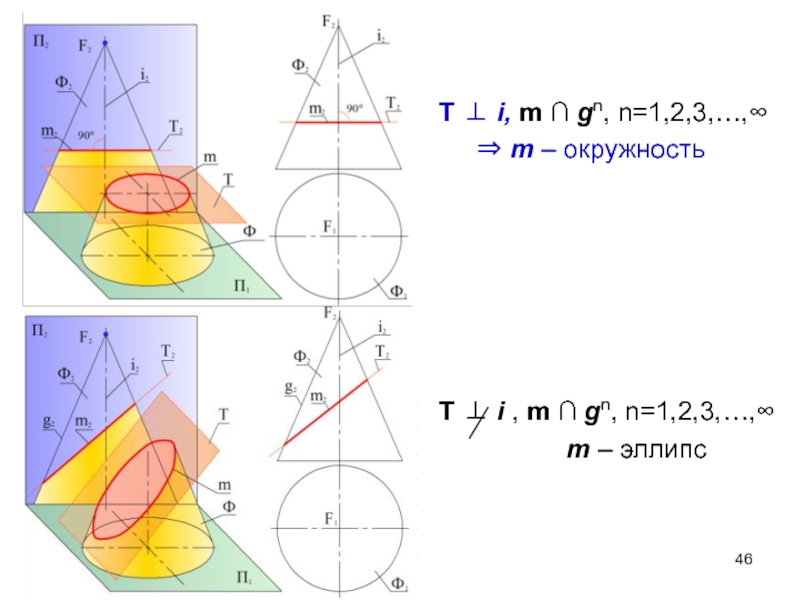
- 46. T ⊥ i, m ∩ gn, n=1,2,3,…,∞
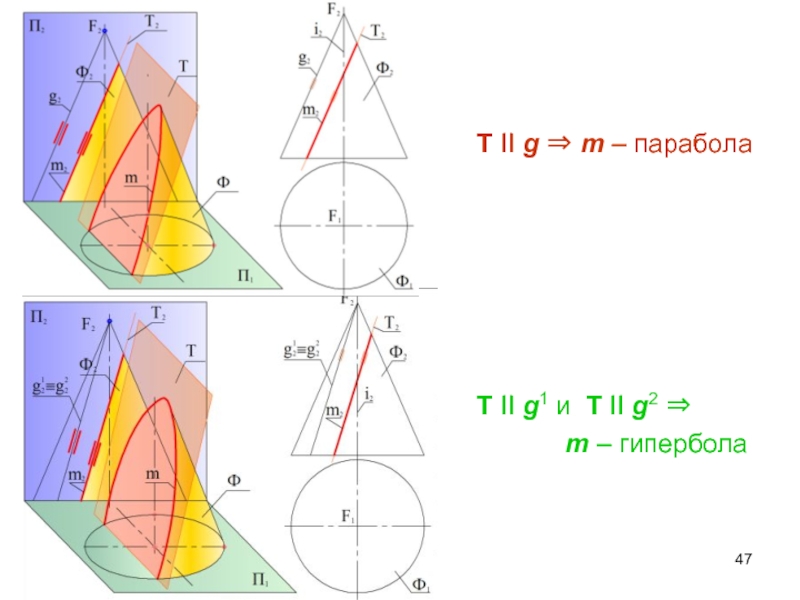
- 47. T II g ⇒ m
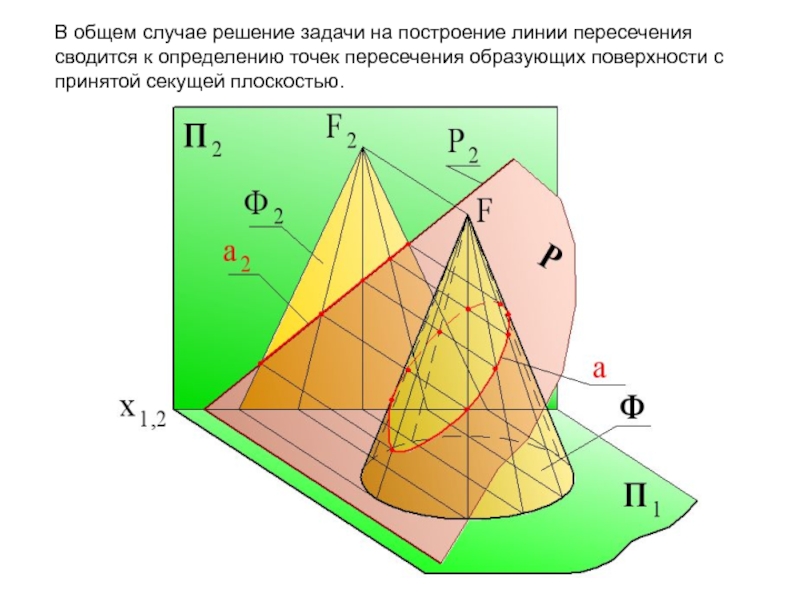
- 48. В общем случае решение задачи на построение
- 49. Данная коническая поверхность относится к классу линейчатых
- 50. Пересечение цилиндрической поверхности плоскостью
- 51. Форма линии пересечения прямой круго-вой цилиндрической поверхности
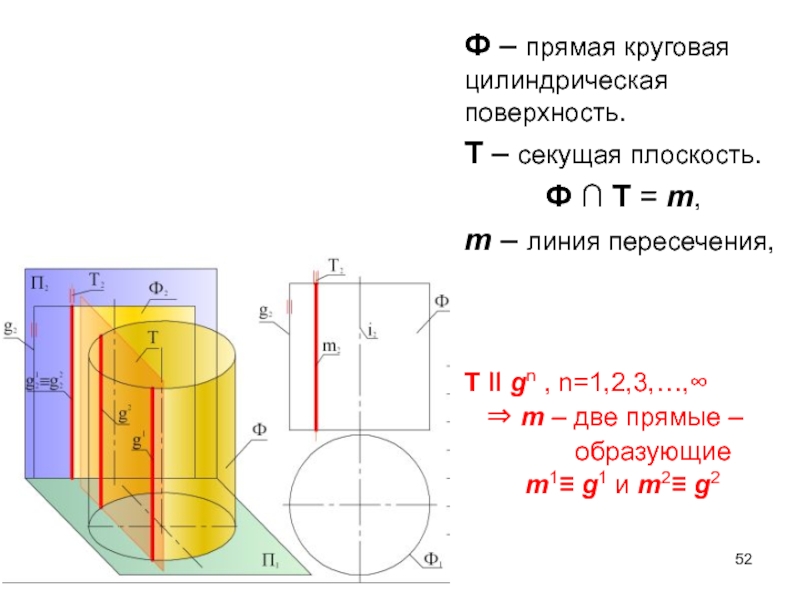
- 52. Ф – прямая круговая цилиндрическая поверхность. Т
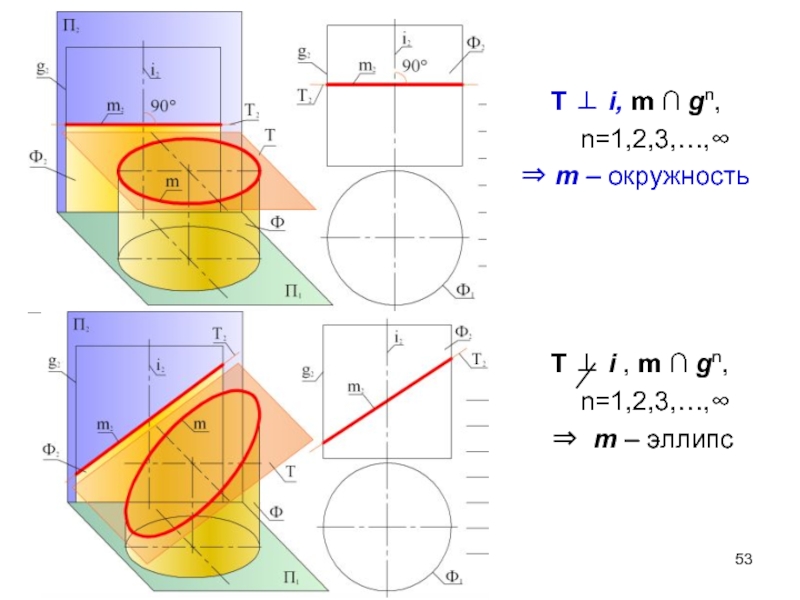
- 53. T ⊥ i, m ∩
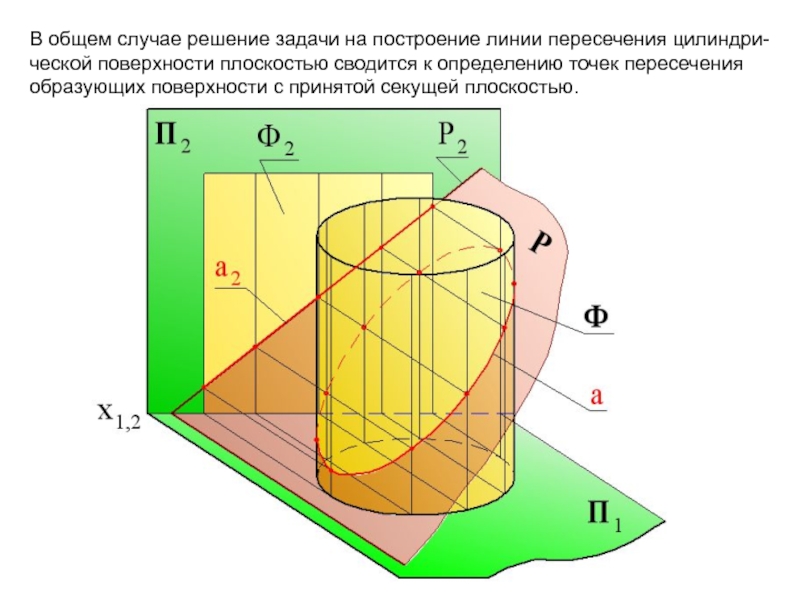
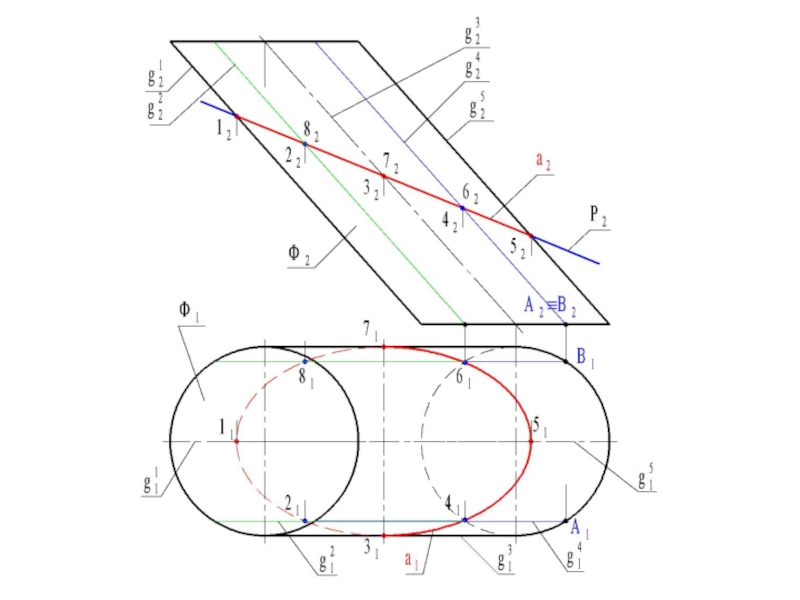
- 54. В общем случае решение задачи на построение
Поверхности
Слайд 4Поверхность – непрерывное двумерное множество точек. Измерения : длина, ширина, площадь.
Толщины и объема нет.
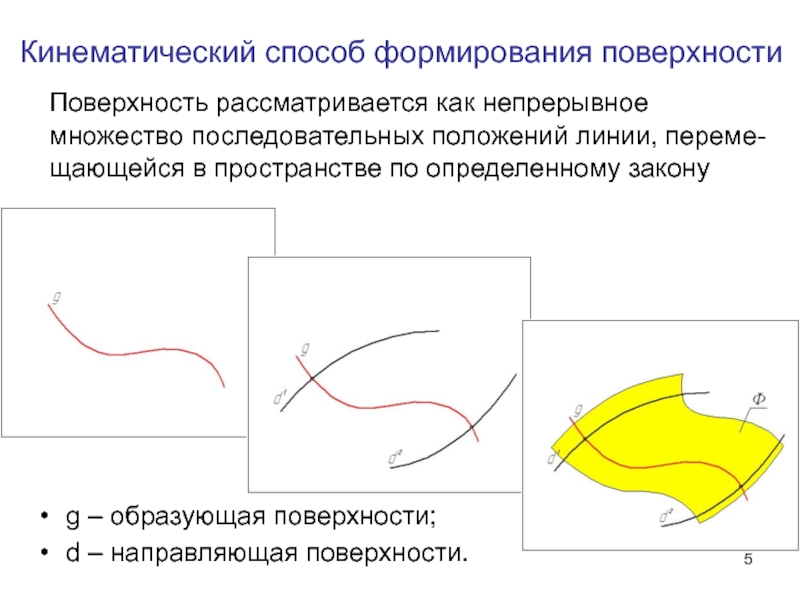
Слайд 5 Поверхность рассматривается как непрерывное множество последовательных положений линии, переме-щающейся
в пространстве по определенному закону
g – образующая поверхности;
d – направляющая поверхности.
Кинематический способ формирования поверхности
Слайд 7Определитель поверхности
Это совокупность независимых условий, однозначно задающих поверхность.
Определитель состоит
из двух частей:
Ф{(Г)(А)}
Геометрическая (Г) - геометрические фигуры - образующая и другие точки, линии, поверхности, участвующие в образова-нии поверхности.
Алгоритмическая (А) – закон перемещения и изменения формы образующей.
Если образующая является прямой линией, которую можно однозначно задать двумя точками или точкой и направлением и графически не изображать, в отличие от кривой линии, то ее обозначение выносят за пределы геометрической части определителя
Ф{g(Г)(А)}
Ф{(Г)(А)}
Геометрическая (Г) - геометрические фигуры - образующая и другие точки, линии, поверхности, участвующие в образова-нии поверхности.
Алгоритмическая (А) – закон перемещения и изменения формы образующей.
Если образующая является прямой линией, которую можно однозначно задать двумя точками или точкой и направлением и графически не изображать, в отличие от кривой линии, то ее обозначение выносят за пределы геометрической части определителя
Ф{g(Г)(А)}
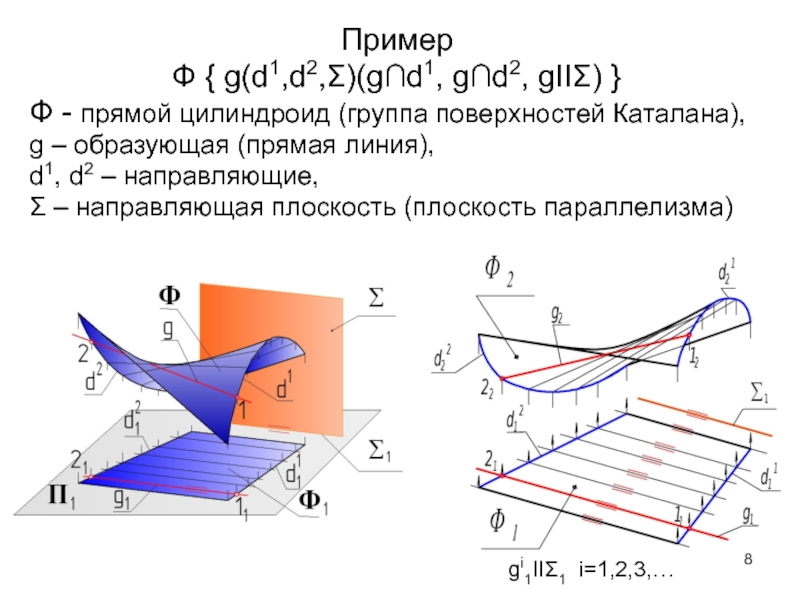
Слайд 8Пример
Ф { g(d1,d2,Σ)(g∩d1, g∩d2, gIIΣ) }
Ф - прямой цилиндроид (группа поверхностей
Каталана),
g – образующая (прямая линия),
d1, d2 – направляющие,
Σ – направляющая плоскость (плоскость параллелизма)
g – образующая (прямая линия),
d1, d2 – направляющие,
Σ – направляющая плоскость (плоскость параллелизма)
gi1IIΣ1 i=1,2,3,…
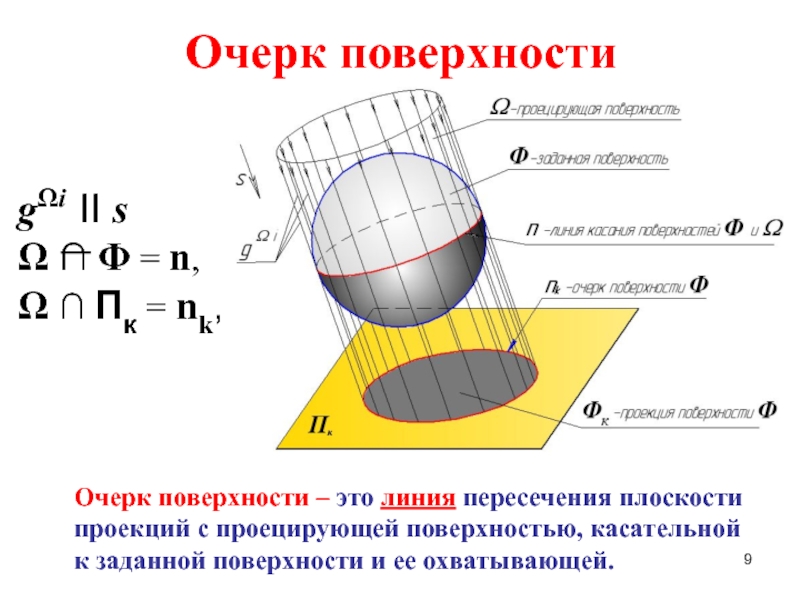
Слайд 9Очерк поверхности
gΩi II s
Ω ∩ Φ = n,
Ω ∩
Пк = nk,
Очерк поверхности – это линия пересечения плоскости
проекций с проецирующей поверхностью, касательной
к заданной поверхности и ее охватывающей.
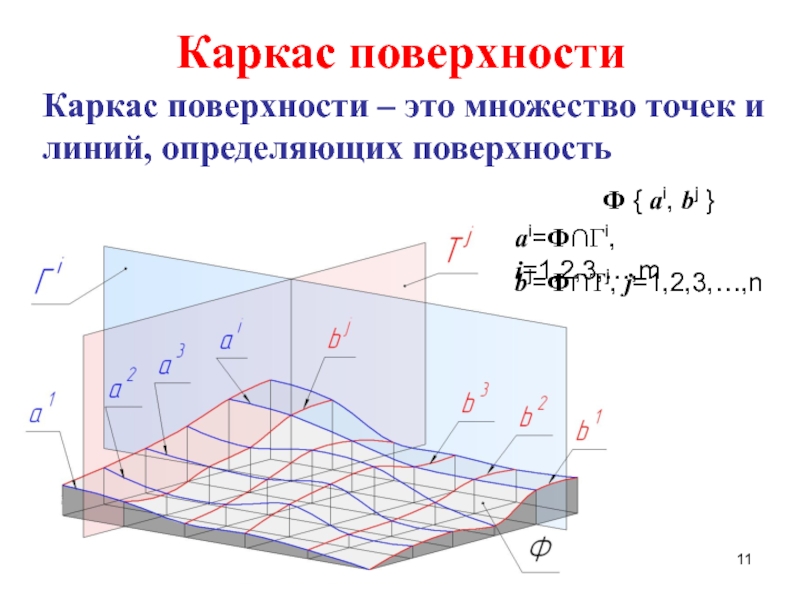
Слайд 11Каркас поверхности
Каркас поверхности – это множество точек и
линий, определяющих поверхность
Ф
{ ai, bj }
ai=Ф∩Гi, i=1,2,3,…,m
bj=Ф∩Tj, j=1,2,3,…,n
Слайд 16С тремя направляющими
Поверхность
косого клина
Поверхность
косого перехода
Ф{g(d1,d2,d3)(g∩d1, g∩d2, g∩d3)}
Слайд 17Ф{g(d1,d2,α)(g∩d1, g∩d2,gIIα)}
Ф{g(d1,d2,α)(g∩d1, g∩d2,
параллелизма (поверхности Каталана)
Гиперболический
параболоид
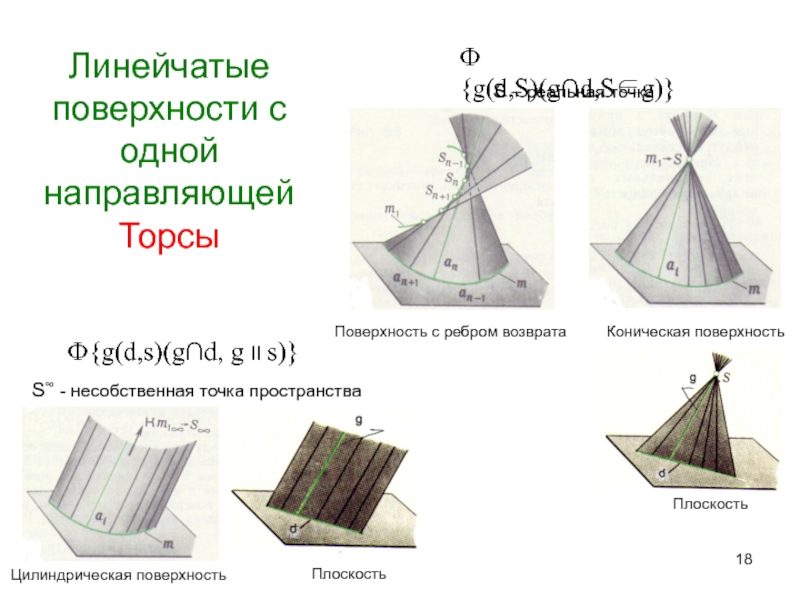
Слайд 18Линейчатые поверхности с одной
направляющей
Торсы
Ф{g(d,s)(g∩d, g II s)}
Ф{g(d,S)(g∩d,S∈g)}
S – реальная точка
S∞
- несобственная точка пространства
Поверхность с ребром возврата
Коническая поверхность
Плоскость
Цилиндрическая поверхность
Плоскость
Слайд 29 Точка принадлежит поверхности, если она принадлежит линии, принадлежащей этой
поверхности
А∈Ф ⇔ А∈ l , l ⊂Ф
Линия l должна на проекциях иметь наиболее простую геометрическую форму: прямая
или окружность (по возможности)
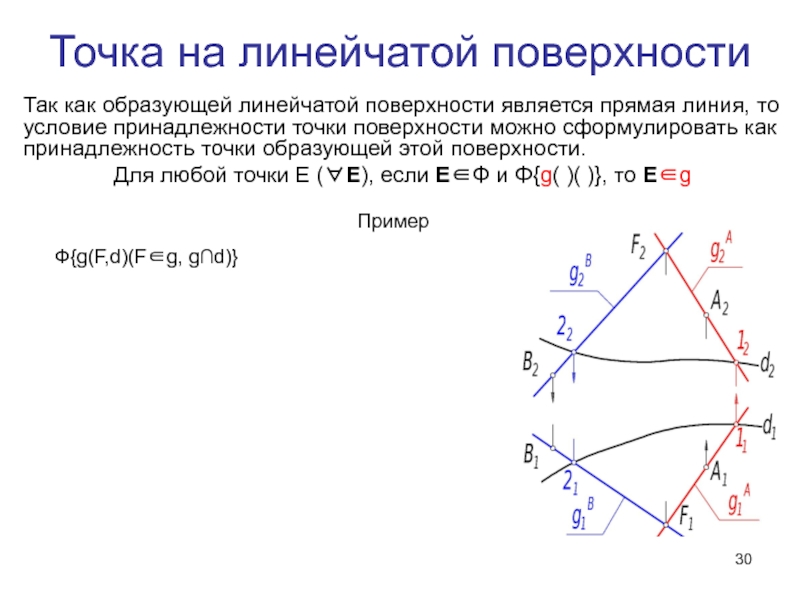
Слайд 30Точка на линейчатой поверхности
Так как образующей линейчатой поверхности является прямая линия,
то условие принадлежности точки поверхности можно сформулировать как принадлежность точки образующей этой поверхности.
Для любой точки Ε (∀Ε), если Ε∈Φ и Φ{g( )( )}, то Ε∈g
Для любой точки Ε (∀Ε), если Ε∈Φ и Φ{g( )( )}, то Ε∈g
Ф{g(F,d)(F∈g, g∩d)}
Пример
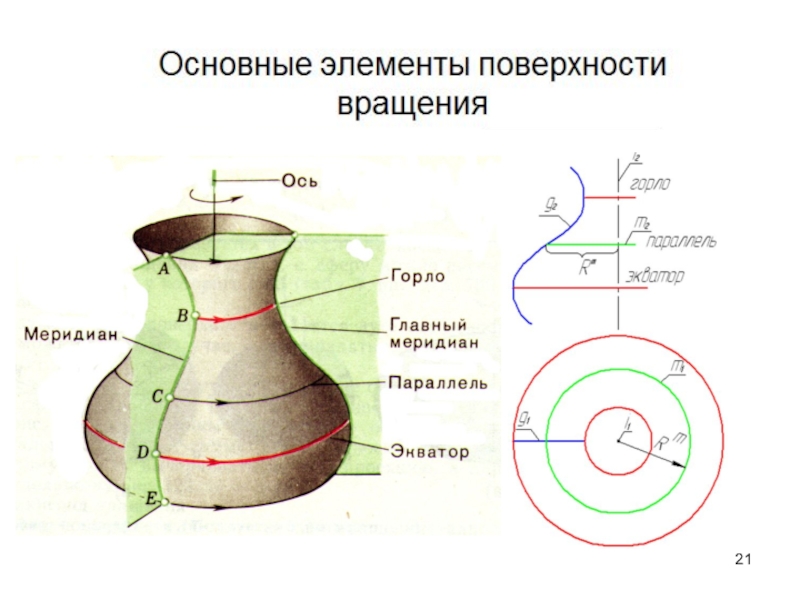
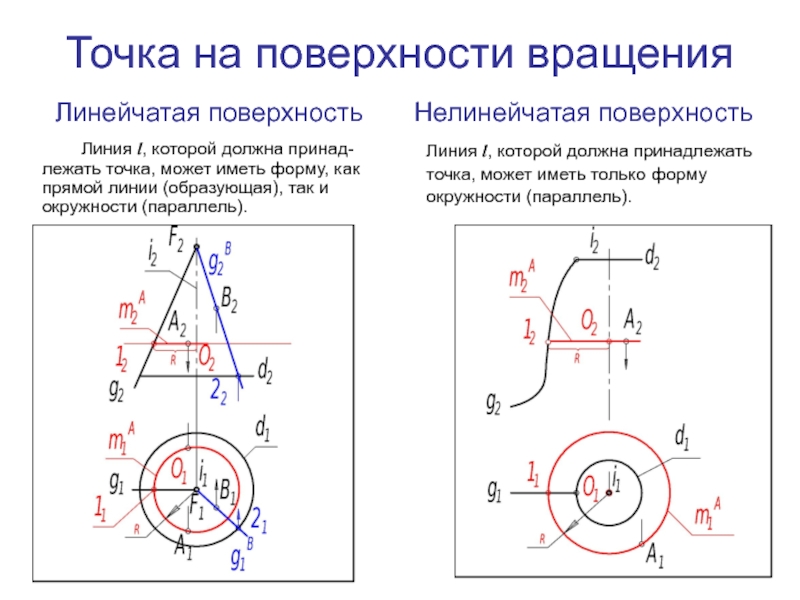
Слайд 31Точка на поверхности вращения
Линия l, которой должна принад-лежать точка, может иметь
форму, как прямой линии (образующая), так и окружности (параллель).
Линейчатая поверхность
Нелинейчатая поверхность
Линия l, которой должна принадлежать точка, может иметь только форму окружности (параллель).
Слайд 33Линия принадлежит поверхности, если все множество ее точек принадлежит этой поверхности.
Следовательно,
чтобы построить линию на поверхности, необходимо представить эту линию, как множество точек, и построить каждую из точек этого множества, используя условие принадлежности точки поверхности.
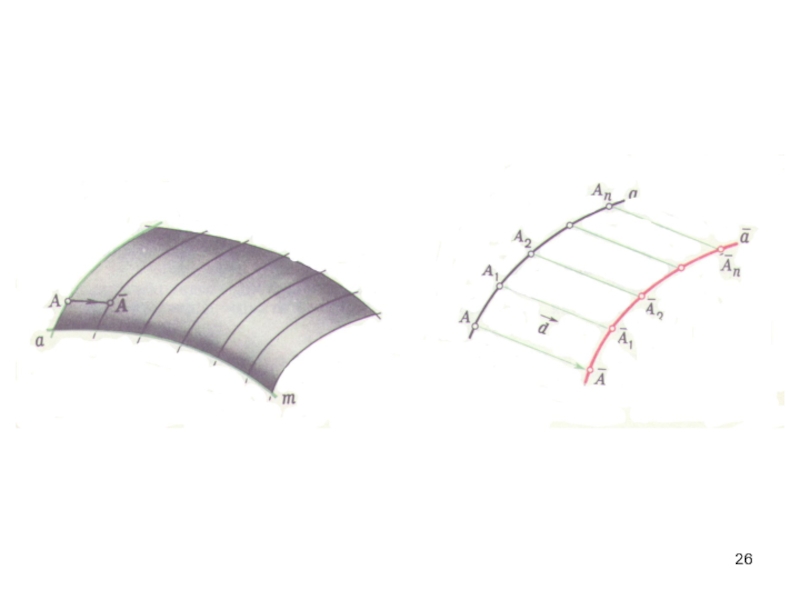
Слайд 34Построение произвольной линии на поверхности
В качестве примера взята цилиндрическая поверхность
общего вида
Ф{g(d,s)(g∩d, g II s)}
Следовательно, для ∀А∈l, точка Α∈g, g∈Ф
l{1,2,3,…}
l⊂Φ ⇒ l{1,2,3,…}⊂Φ
Φ - линейчатая поверхность
Слайд 37Линию пересечения поверхности плоскостью следует рассматривать как множество точек пересечения секущей
плоскости с линиями, принадлежащими поверхности.
Форма линии пересечения поверхности плоскостью определяется формой заданной поверхности и положением плоскости относительно этой поверхности.
Для кривой поверхности, в общем случае, линия пересечения - это плоская кривая линия.
Форма линии пересечения поверхности плоскостью определяется формой заданной поверхности и положением плоскости относительно этой поверхности.
Для кривой поверхности, в общем случае, линия пересечения - это плоская кривая линия.
Слайд 38Из всего множества точек линии пересечения должны быть обязательно построены следующие
точки:
точки, определяющие габариты формы фигуру сечения;
точки, определяющие габариты фигуры сечения по высоте, глубине и длине;
точки, определяющие видимость фигуры сечения на проекциях.
точки, определяющие габариты формы фигуру сечения;
точки, определяющие габариты фигуры сечения по высоте, глубине и длине;
точки, определяющие видимость фигуры сечения на проекциях.
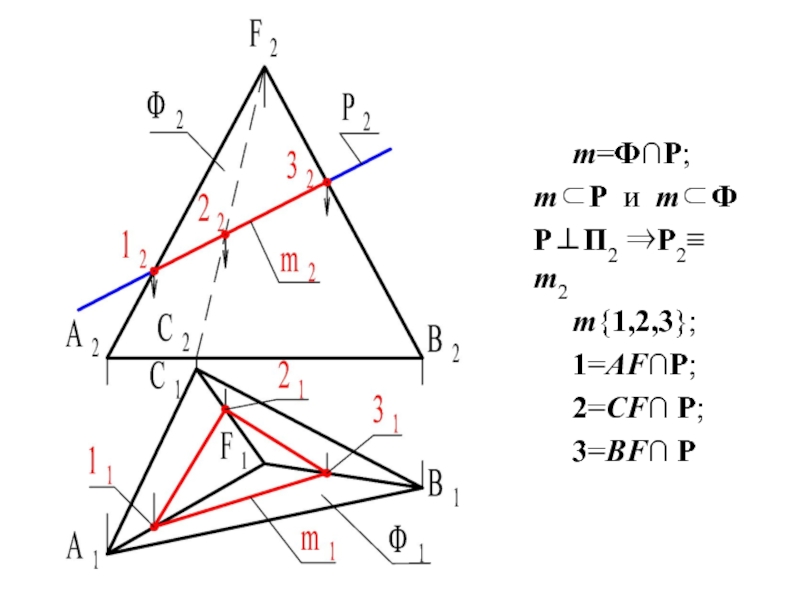
Слайд 40При пересечении гранной поверхности плоскостью линия пересечения – это ломаная линия,
каждый участок которой – отрезок прямой, представляющий собой линию пересечения грани поверхности (отсека плоскости) с секущей плоскостью, а точки излома – точки пересечения ребер гранной поверхности (отрезков прямых) с той же секущей плоскостью.
Следовательно, решение задачи на построение линии пересечения сводится к определению точек пересечения ребер гранной поверхности с принятой секущей плоскостью.
Следовательно, решение задачи на построение линии пересечения сводится к определению точек пересечения ребер гранной поверхности с принятой секущей плоскостью.
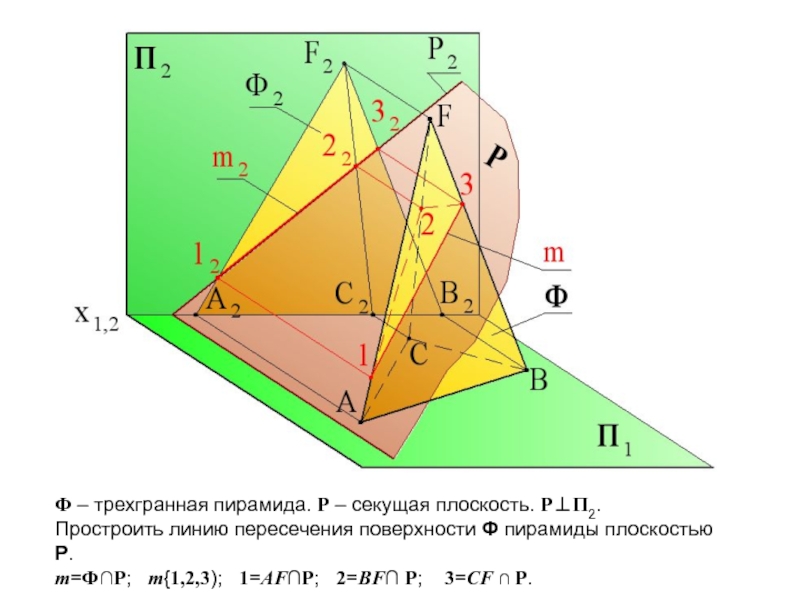
Слайд 41Ф – трехгранная пирамида. Р – секущая плоскость. Р⊥П2.
Простроить линию пересечения
поверхности Ф пирамиды плоскостью Р.
m=Ф∩Р; m{1,2,3); 1=AF∩P; 2=BF∩ P; 3=CF ∩ P.
m=Ф∩Р; m{1,2,3); 1=AF∩P; 2=BF∩ P; 3=CF ∩ P.
Слайд 44При пересечении прямой круговой конической поверхности плоскостью форма линии пересечения определяется
положением секущей плоскости относительно отдельных элементов поверхности.
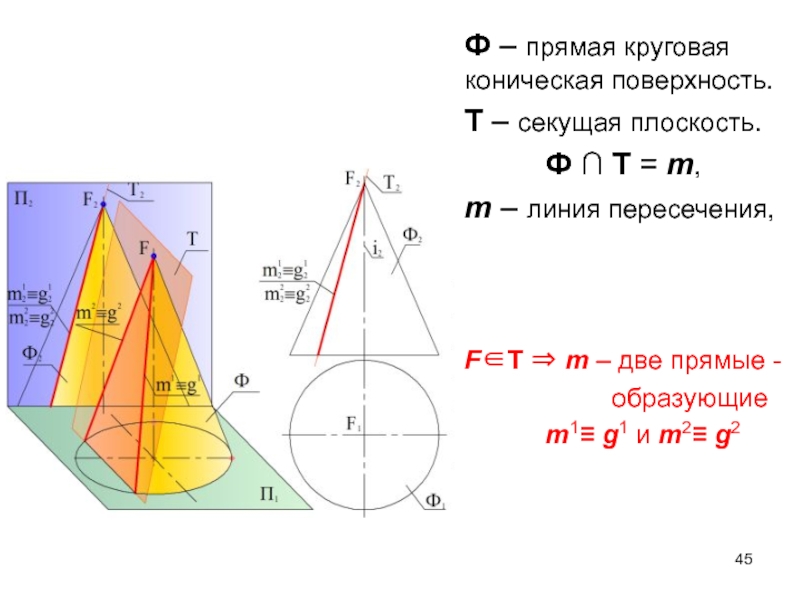
Слайд 45Ф – прямая круговая коническая поверхность.
Т – секущая плоскость.
Ф ∩ Т
= m,
m – линия пересечения,
F∈T ⇒ m – две прямые -
образующие
m1≡ g1 и m2≡ g2
m – линия пересечения,
F∈T ⇒ m – две прямые -
образующие
m1≡ g1 и m2≡ g2
Слайд 48В общем случае решение задачи на построение линии пересечения сводится к
определению точек пересечения образующих поверхности с принятой секущей плоскостью.
Слайд 49Данная коническая поверхность относится к классу линейчатых и подклассу поверхностей вращения.
Следовательно, для построения точки на поверхности можно использовать, как прямую линия (образующую), так и окружность (параллель).
Слайд 51Форма линии пересечения прямой круго-вой цилиндрической поверхности плоскос-тью, так же как
и при пересечении прямой круговой конической поверхности, опреде-ляется положением секущей плоскости отно-сительно отдельных элементов поверхности.
Слайд 52Ф – прямая круговая цилиндрическая поверхность.
Т – секущая плоскость.
Ф ∩ Т
= m,
m – линия пересечения,
Т II gn , n=1,2,3,…,∞
⇒ m – две прямые –
образующие
m1≡ g1 и m2≡ g2
m – линия пересечения,
Т II gn , n=1,2,3,…,∞
⇒ m – две прямые –
образующие
m1≡ g1 и m2≡ g2
Слайд 54В общем случае решение задачи на построение линии пересечения цилиндри-ческой поверхности
плоскостью сводится к определению точек пересечения образующих поверхности с принятой секущей плоскостью.
