вертикальной вспомогательной стенки
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Построение перспективы методом архитекторов с опущенным (поднятым) планом презентация
Содержание
- 1. Построение перспективы методом архитекторов с опущенным (поднятым) планом
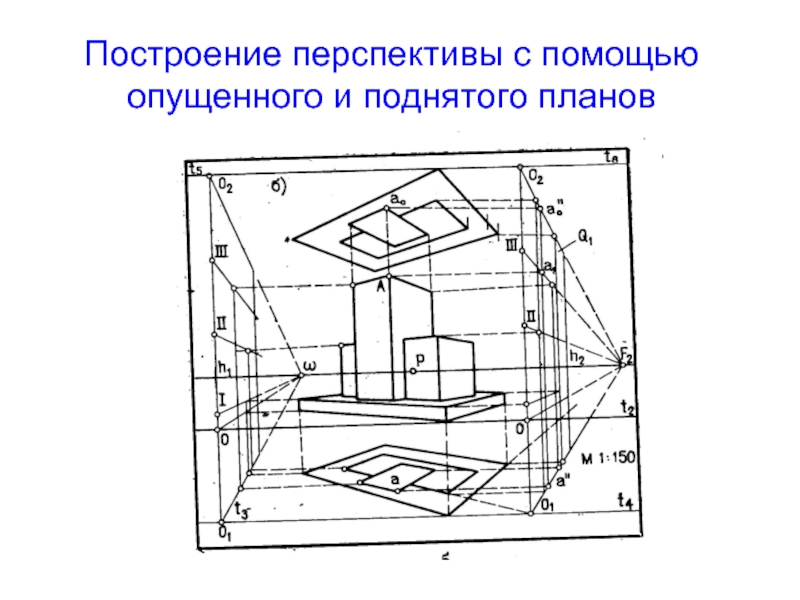
- 2. Построение перспективы с помощью опущенного и поднятого планов
- 3. Применение дополнительного плана В случаях, когда высота
- 4. Применение дополнительной плоскости П2 оk1- основание картины
- 5. Применение дополнительной плоскости П2 Разместим в предметном
- 6. Применение дополнительной вертикальной плоскости На оси
- 7. Определение глубины расположения объекта Определим координату Уа,в
- 8. Определим высоту объекта на заданной глубине
- 9. Рассмотрим пример построения перспективы с применением опущенного
- 10. Из крайних точек объекта опустим перпендикуляры к
- 11. Предположим, что построение перспективы будем вести в
- 12. На линии горизонта задаем положение точек схода
- 13. Построение перспективы плана объекта выполняем на нижней
- 14. Рассмотрим разные варианты построения точек 2 и
- 15. Определим положение точки 3 плана , как
- 16. Завершаем построение перспективы плиты основания объекта
- 17. С помощью теоремы Фалеса построим остальные элементы
- 18. Перенесем пропорцию на перспективу прямой 2-1 h
- 19. С помощью точки схода F2 получим перспективы
- 20. Перенесем пропорцию на перспективу прямой 2-3. Через
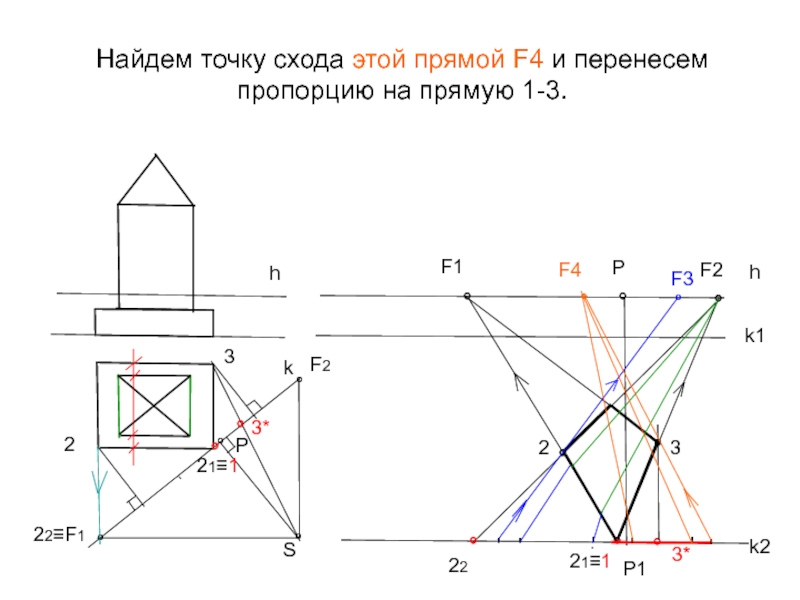
- 21. Найдем точку схода этой прямой F4 и
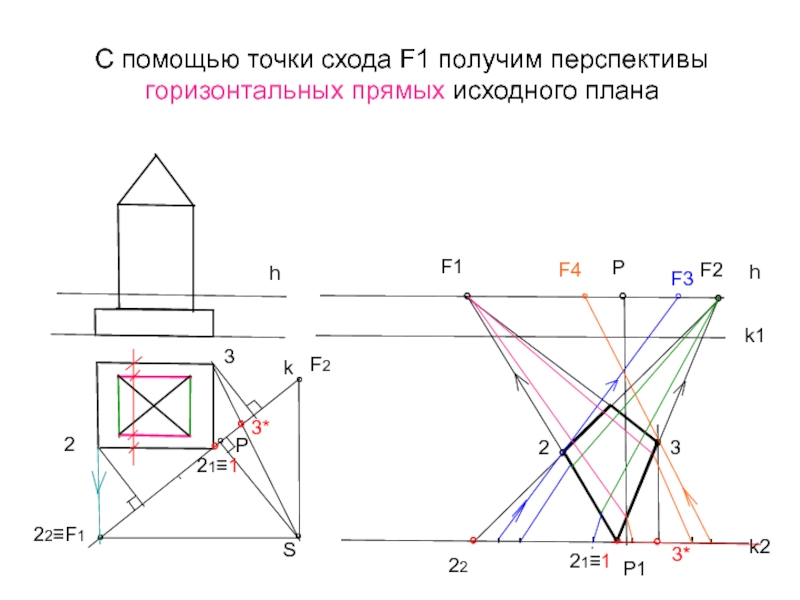
- 22. С помощью точки схода F1 получим перспективы
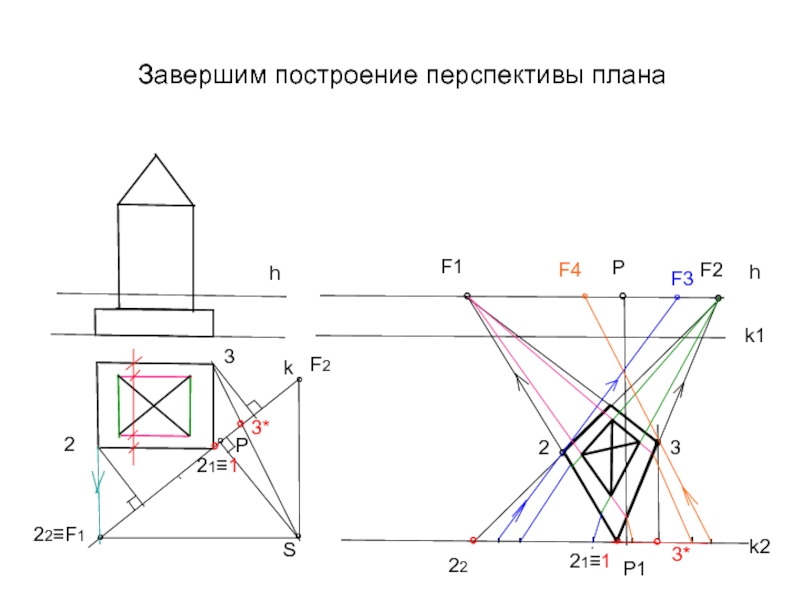
- 23. Завершим построение перспективы плана h k
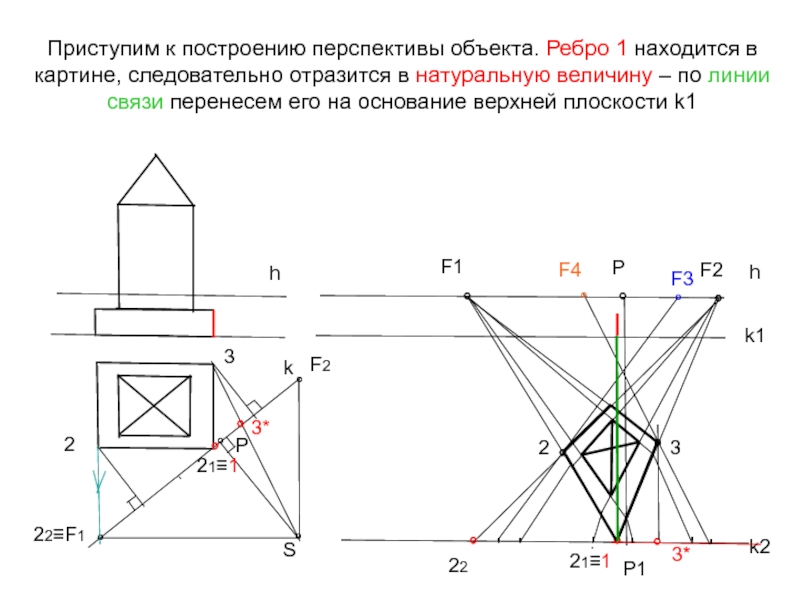
- 24. Приступим к построению перспективы объекта. Ребро 1
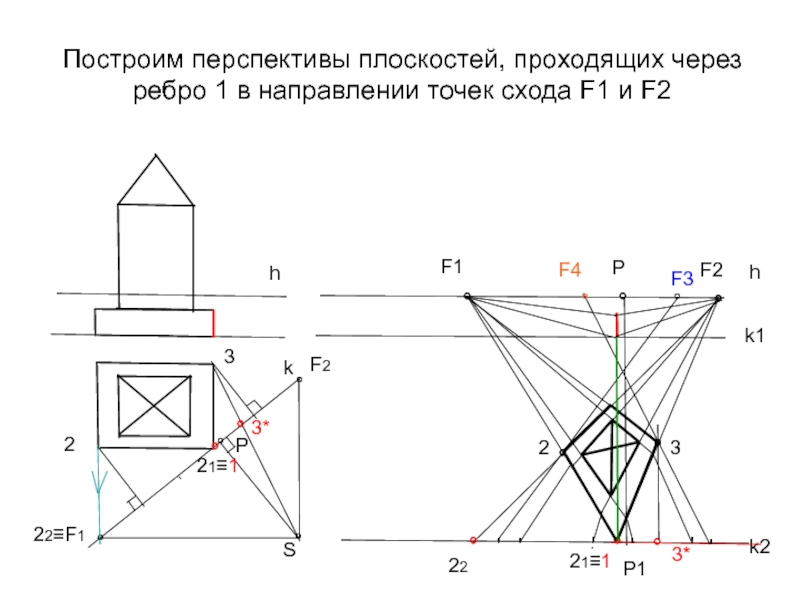
- 25. Построим перспективы плоскостей, проходящих через ребро 1
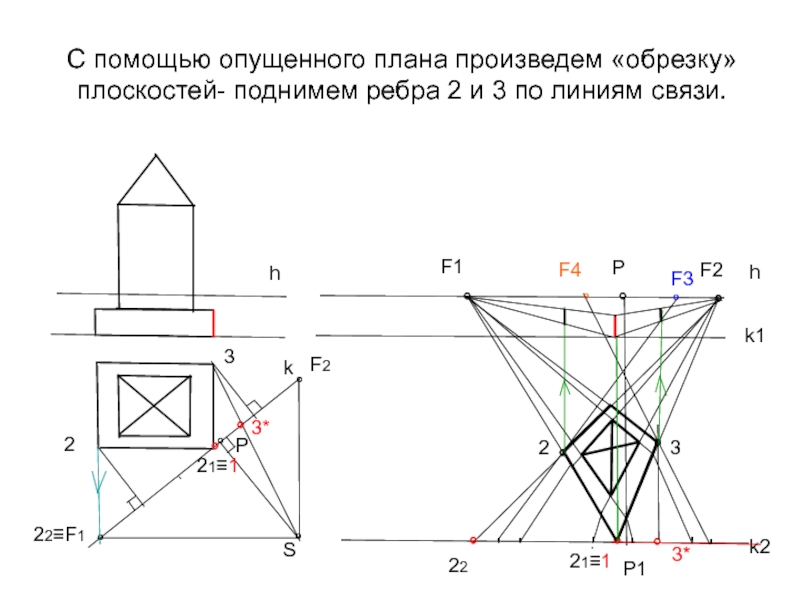
- 26. С помощью опущенного плана произведем «обрезку» плоскостей-
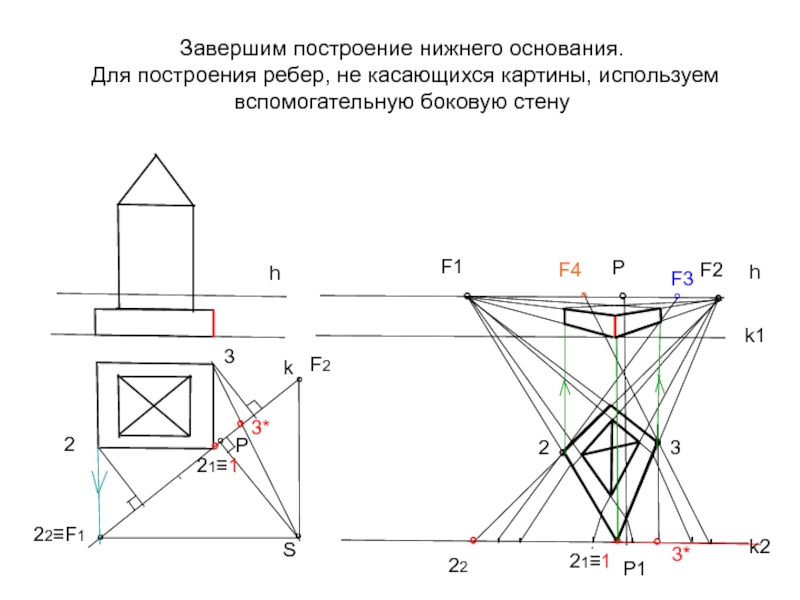
- 27. Завершим построение нижнего основания. Для построения
- 28. Применение вспомогательной вертикальной плоскости (боковой стены) Боковая
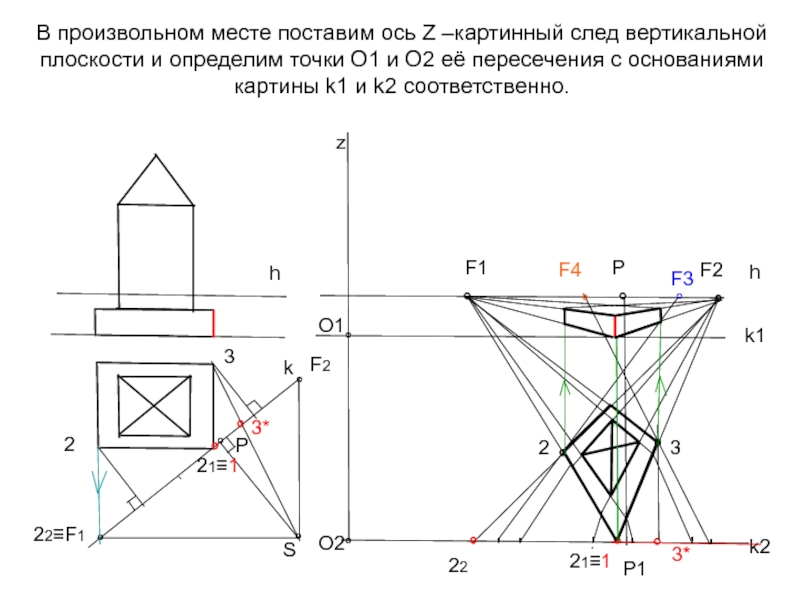
- 29. В произвольном месте поставим ось Z –картинный
- 30. На линии горизонта возьмем произвольно точку схода
- 31. Для построения вертикального ребра 4 отложим на
- 32. Через точку 4 перспективного плана проведем прямую,
- 33. Перенесем полученный размер параллельно картине в верхнем
- 34. Построим перспективы плоскостей, проходящих через ребро 4
- 35. По линиям связи определим положение ребер 5
- 36. Завершим построение верхнего объема и нижнего основания
- 37. Построим перспективу пиковой точки 7.На оси z
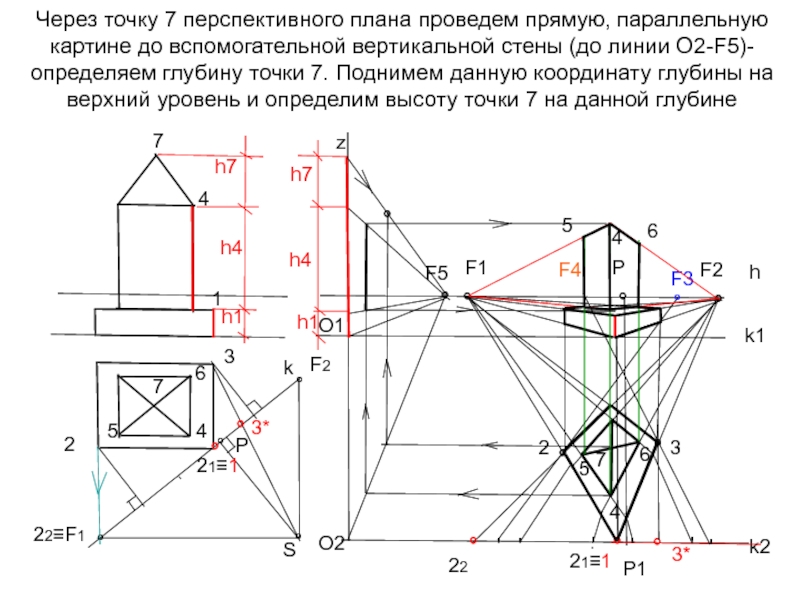
- 38. Через точку 7 перспективного плана проведем прямую,
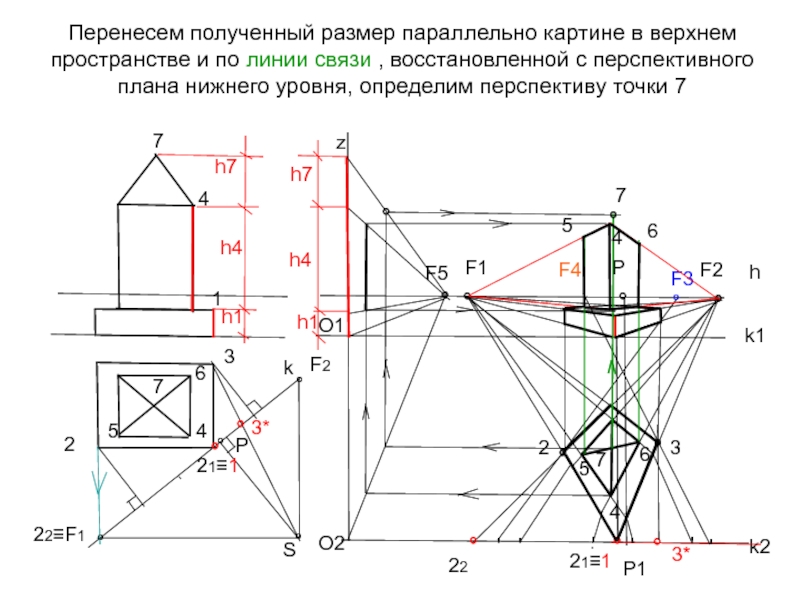
- 39. Перенесем полученный размер параллельно картине в верхнем
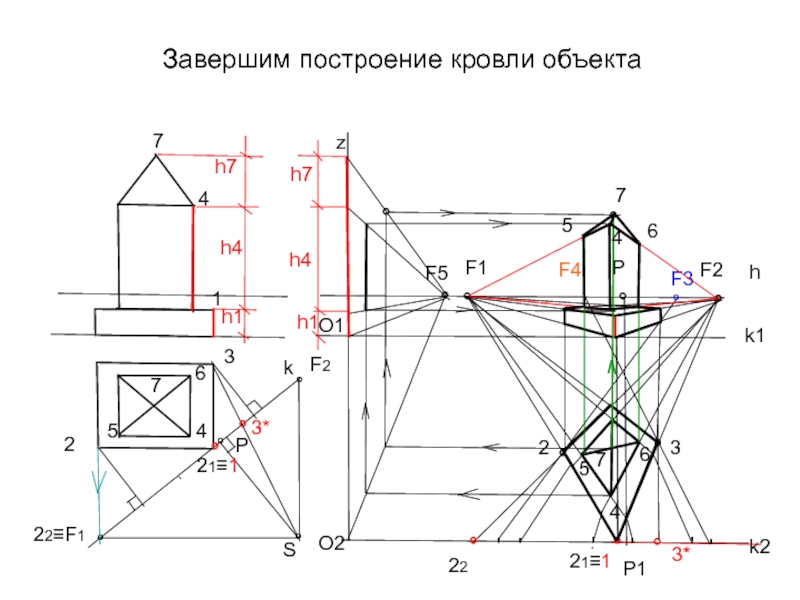
- 40. Завершим построение кровли объекта h4 k °
Построение перспективы с помощью опущенного и поднятого планов
Слайд 1Лекция 20
Построение перспективы методом архитекторов с опущенным (поднятым) планом
Построение опущенного плана
Построение
Слайд 3Применение дополнительного плана
В случаях, когда высота горизонта мала и вторичная проекция
объекта оказывается сжатой, что затрудняет дальнейшие построения на перспективе плана, применяют горизонтальную вспомогательную плоскость.
Перспективу плана строят не на предметной плоскости, а на вспомогательной, опущенной вниз от предметной плоскости на произвольное расстояние или поднятой вверх
Перспективу плана строят не на предметной плоскости, а на вспомогательной, опущенной вниз от предметной плоскости на произвольное расстояние или поднятой вверх
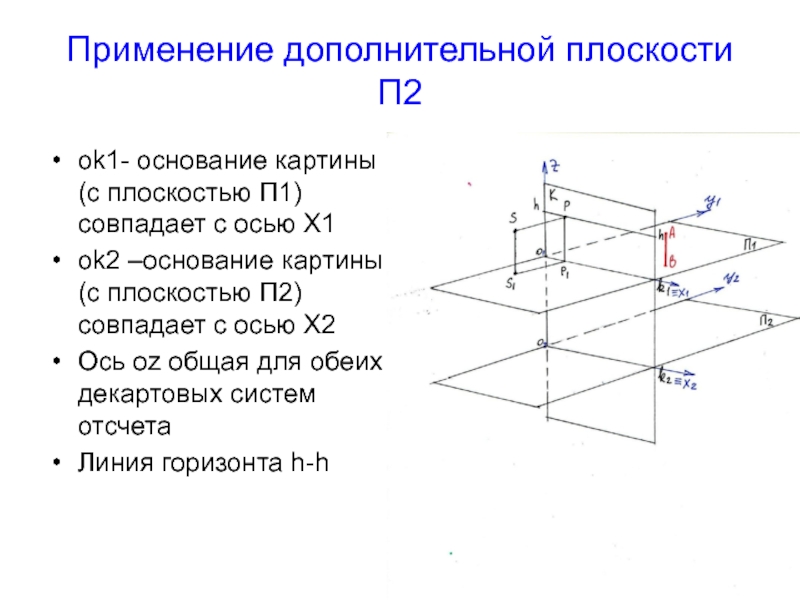
Слайд 4Применение дополнительной плоскости П2
оk1- основание картины (с плоскостью П1) совпадает с
осью Х1
ok2 –основание картины (с плоскостью П2) совпадает с осью Х2
Ось оz общая для обеих декартовых систем отсчета
Линия горизонта h-h
ok2 –основание картины (с плоскостью П2) совпадает с осью Х2
Ось оz общая для обеих декартовых систем отсчета
Линия горизонта h-h
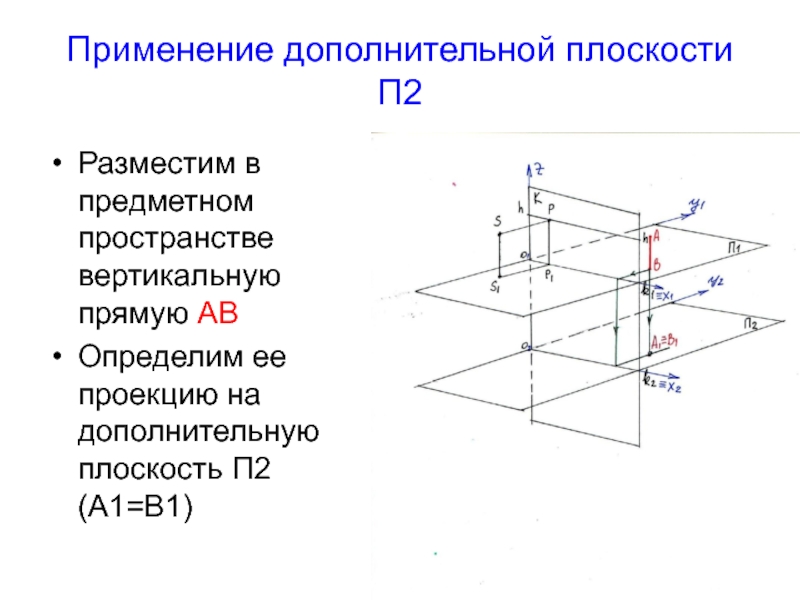
Слайд 5Применение дополнительной плоскости П2
Разместим в предметном пространстве вертикальную прямую АВ
Определим ее
проекцию на дополнительную плоскость П2 (А1=В1)
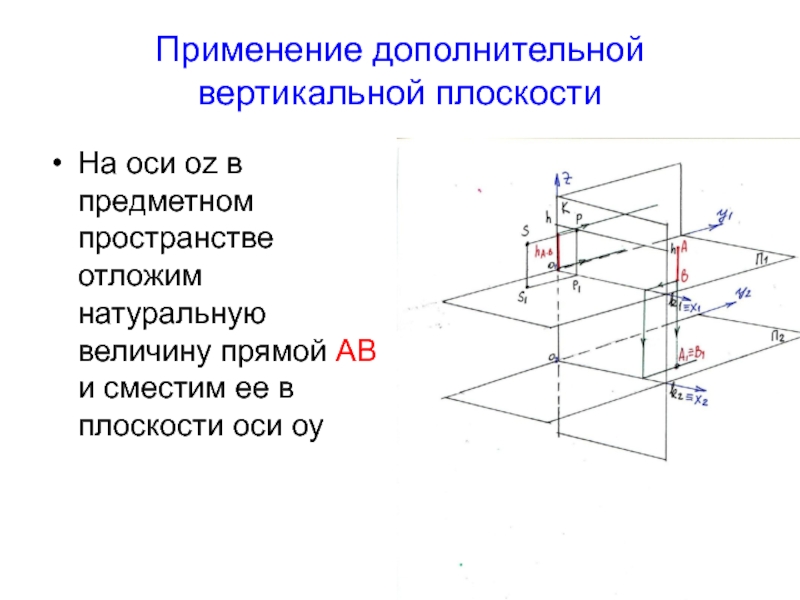
Слайд 6Применение дополнительной вертикальной плоскости
На оси oz в предметном пространстве отложим
натуральную величину прямой АВ и сместим ее в плоскости оси оу
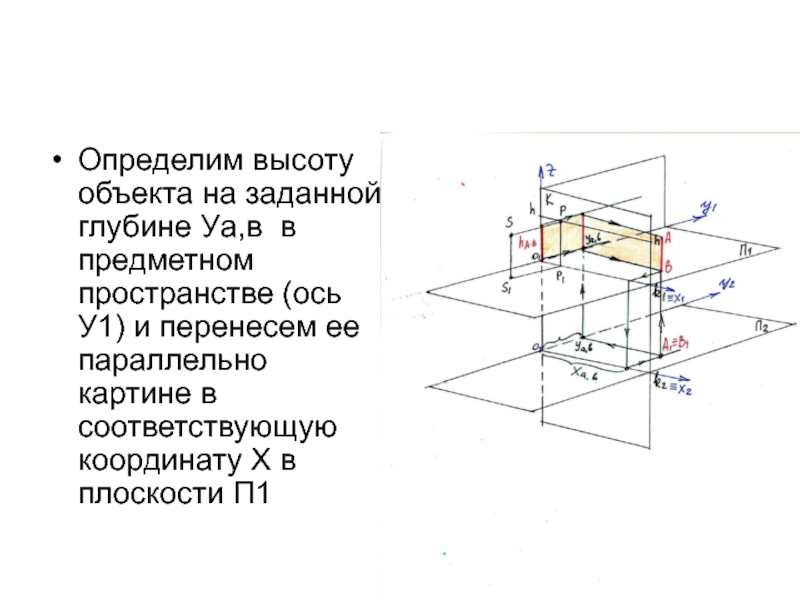
Слайд 7Определение глубины расположения объекта
Определим координату Уа,в на дополнительной плоскости П2
Перенесем ее
на предметную плоскость П1
Слайд 8
Определим высоту объекта на заданной глубине Уа,в в предметном пространстве (ось
У1) и перенесем ее параллельно картине в соответствующую координату Х в плоскости П1
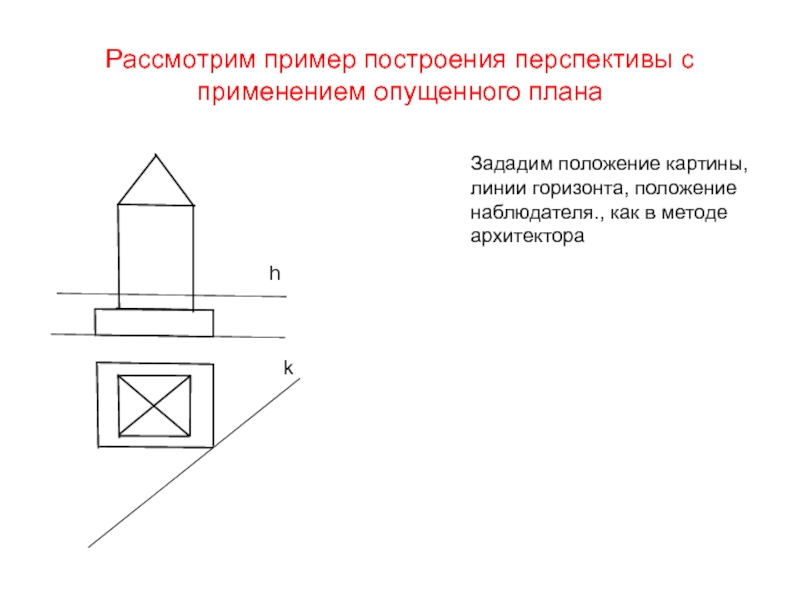
Слайд 9Рассмотрим пример построения перспективы с применением опущенного плана
h
k
Зададим положение картины,
линии
горизонта, положение
наблюдателя., как в методе
архитектора
наблюдателя., как в методе
архитектора
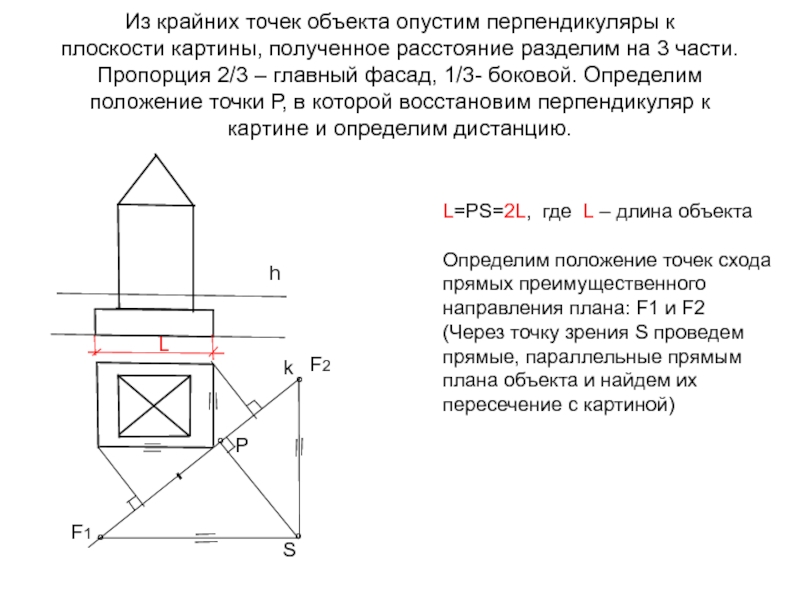
Слайд 10Из крайних точек объекта опустим перпендикуляры к плоскости картины, полученное расстояние
разделим на 3 части. Пропорция 2/3 – главный фасад, 1/3- боковой. Определим положение точки Р, в которой восстановим перпендикуляр к картине и определим дистанцию.
h
k
°
Р
°
S
°
F1
°
F2
L=РS=2L, где L – длина объекта
Определим положение точек схода прямых преимущественного направления плана: F1 и F2
(Через точку зрения S проведем прямые, параллельные прямым плана объекта и найдем их пересечение с картиной)
L
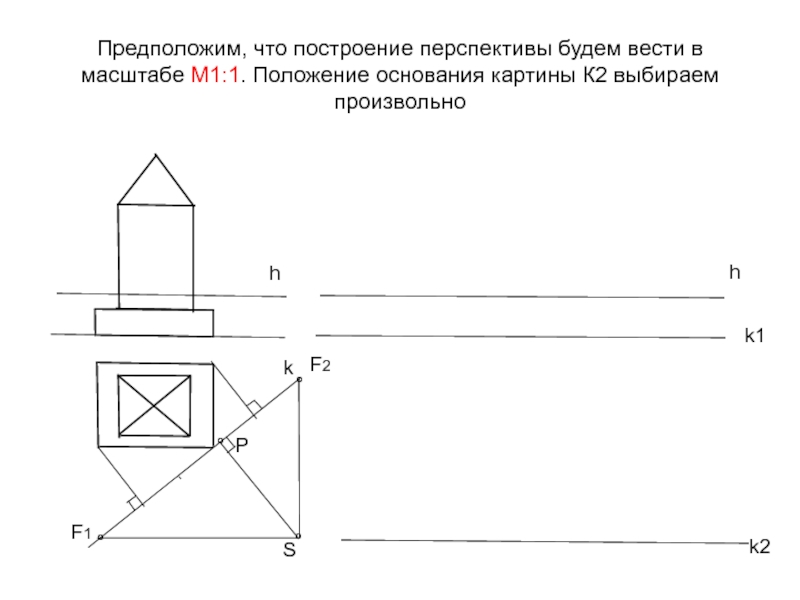
Слайд 11Предположим, что построение перспективы будем вести в масштабе М1:1. Положение основания
картины К2 выбираем произвольно
h
k
°
Р
°
S
°
F1
°
F2
h
k1
k2
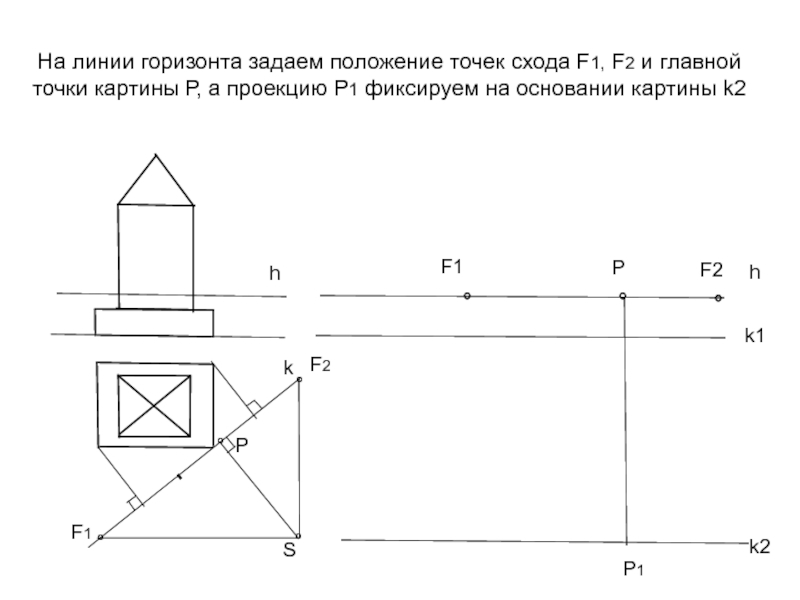
Слайд 12На линии горизонта задаем положение точек схода F1, F2 и главной
точки картины Р, а проекцию Р1 фиксируем на основании картины k2
h
k
°
Р
°
S
°
F1
°
F2
h
k1
k2
°
°
°
F1
F2
Р
Р1
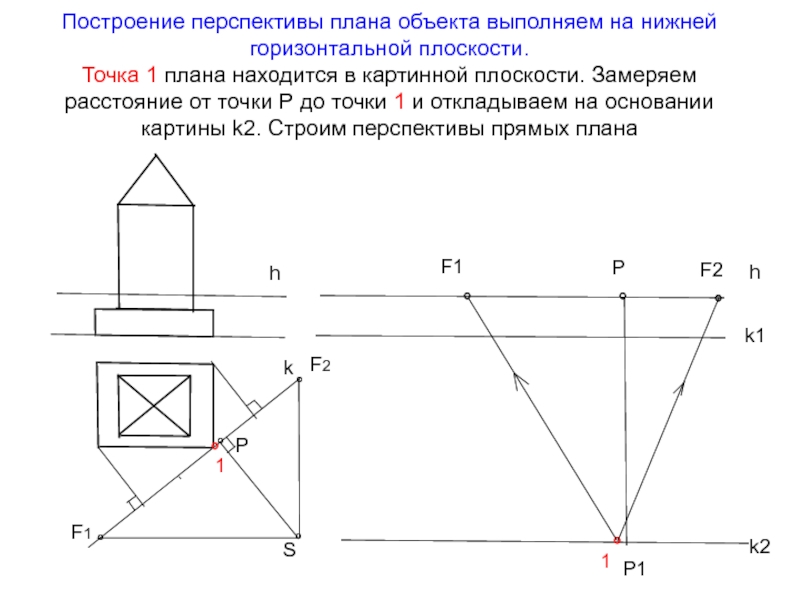
Слайд 13Построение перспективы плана объекта выполняем на нижней горизонтальной плоскости. Точка 1
плана находится в картинной плоскости. Замеряем расстояние от точки Р до точки 1 и откладываем на основании картины k2. Строим перспективы прямых плана
h
k
°
Р
°
S
°
F1
°
F2
h
k1
k2
°
°
°
F1
F2
Р
Р1
°
1
°
1
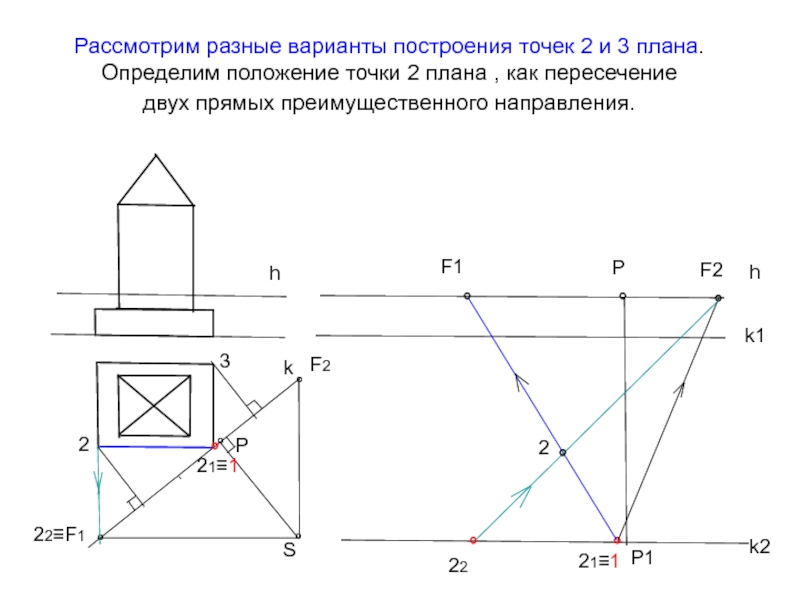
Слайд 14Рассмотрим разные варианты построения точек 2 и 3 плана. Определим положение
точки 2 плана , как пересечение
двух прямых преимущественного направления.
h
k
°
Р
°
S
°
22≡F1
°
F2
h
k1
k2
°
°
°
F1
F2
Р
Р1
°
21≡1
°
21≡1
2
°
22
°
2
3
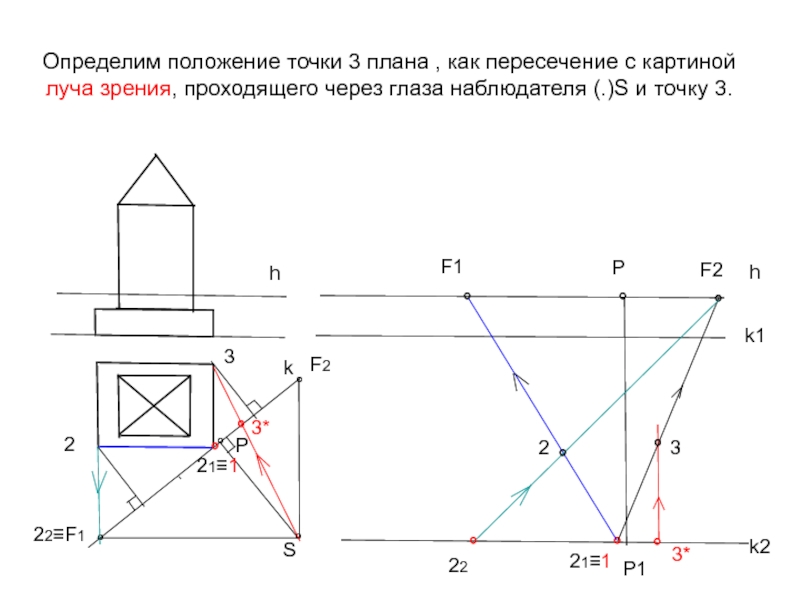
Слайд 15Определим положение точки 3 плана , как пересечение с картиной луча
зрения, проходящего через глаза наблюдателя (.)S и точку 3.
h
k
°
Р
°
S
°
22≡F1
°
F2
h
k1
k2
°
°
°
F1
F2
Р
Р1
°
21≡1
°
21≡1
2
°
22
°
2
3
°
3*
°
3*
°
3
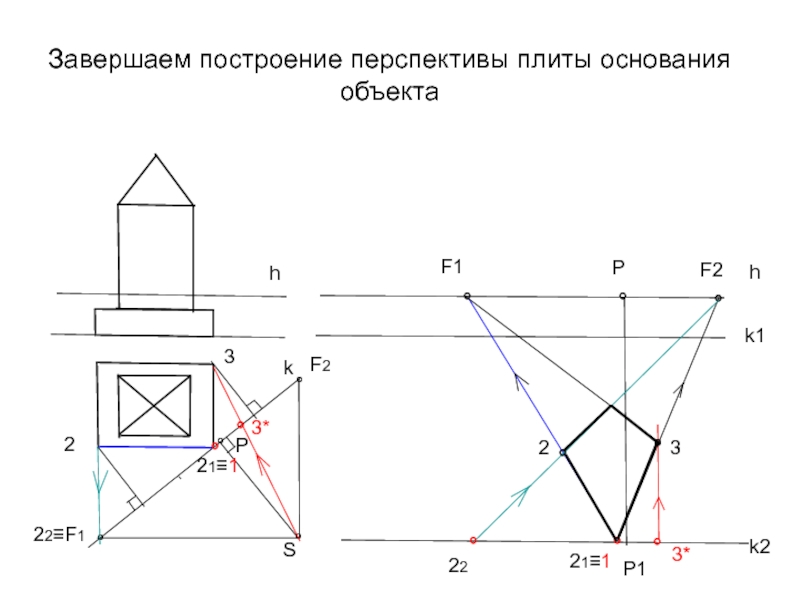
Слайд 16Завершаем построение перспективы плиты основания объекта
h
k
°
Р
°
S
°
22≡F1
°
F2
h
k1
k2
°
°
°
F1
F2
Р
Р1
°
21≡1
°
21≡1
2
°
22
°
2
3
°
3*
°
3*
°
3
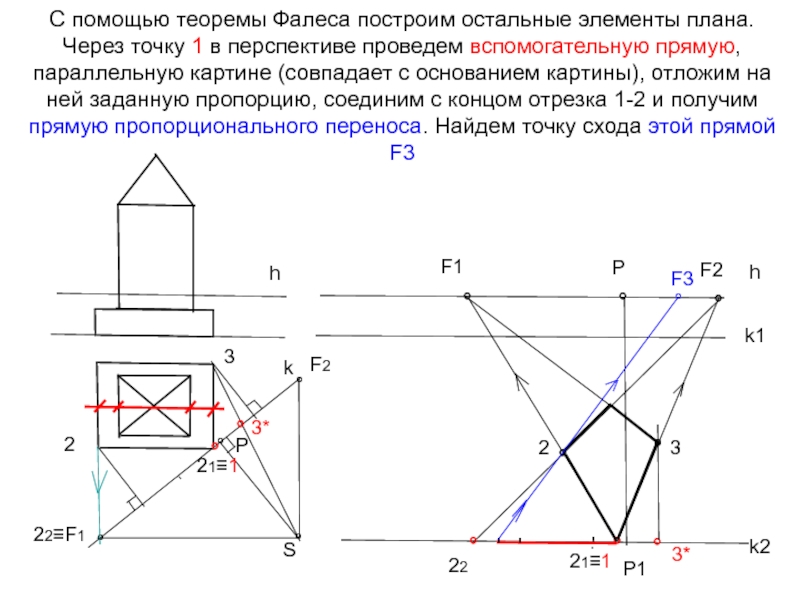
Слайд 17С помощью теоремы Фалеса построим остальные элементы плана. Через точку 1
в перспективе проведем вспомогательную прямую, параллельную картине (совпадает с основанием картины), отложим на ней заданную пропорцию, соединим с концом отрезка 1-2 и получим прямую пропорционального переноса. Найдем точку схода этой прямой F3
h
k
°
Р
°
S
°
22≡F1
°
F2
h
k1
k2
°
°
°
F1
F2
Р
Р1
°
21≡1
°
21≡1
2
°
22
°
2
3
°
3*
°
3*
°
3
'
'
'
F3
°
Слайд 18Перенесем пропорцию на перспективу прямой 2-1
h
k
°
Р
°
S
°
22≡F1
°
F2
h
k1
k2
°
°
°
F1
F2
Р
Р1
°
21≡1
°
21≡1
2
°
22
°
2
3
°
3*
°
3*
°
3
'
'
'
F3
°
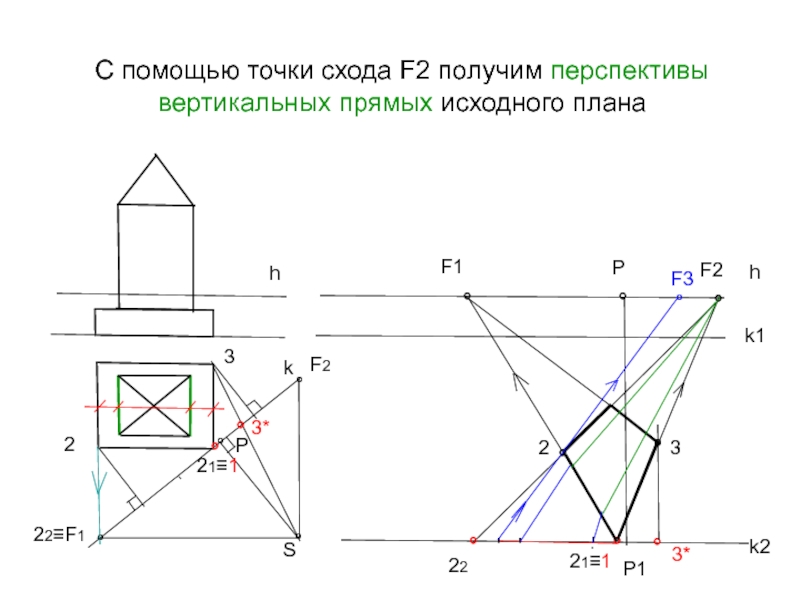
Слайд 19С помощью точки схода F2 получим перспективы вертикальных прямых исходного плана
h
k
°
Р
°
S
°
22≡F1
°
F2
h
k1
k2
°
°
°
F1
F2
Р
Р1
°
21≡1
°
21≡1
2
°
22
°
2
3
°
3*
°
3*
°
3
'
'
'
F3
°
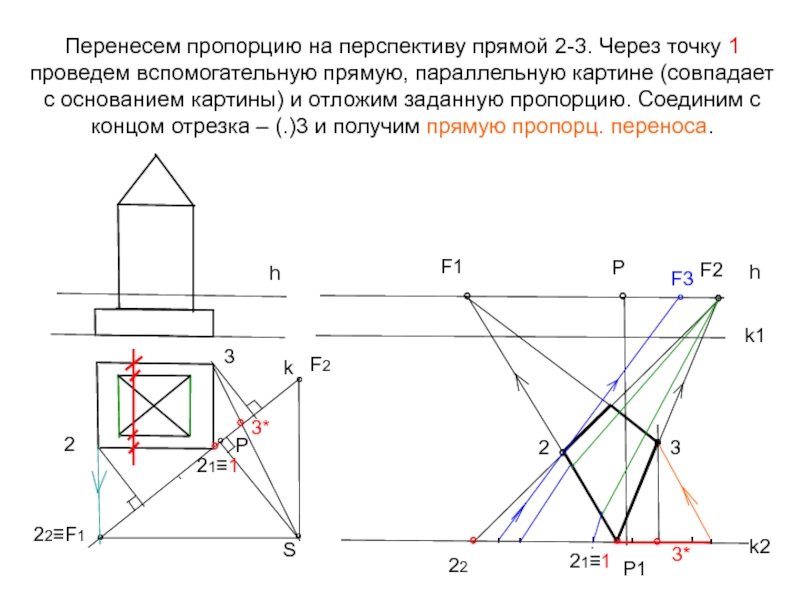
Слайд 20Перенесем пропорцию на перспективу прямой 2-3. Через точку 1 проведем вспомогательную
прямую, параллельную картине (совпадает с основанием картины) и отложим заданную пропорцию. Соединим с концом отрезка – (.)3 и получим прямую пропорц. переноса.
h
k
°
Р
°
S
°
22≡F1
°
F2
h
k1
k2
°
°
°
F1
F2
Р
Р1
°
21≡1
°
21≡1
2
°
22
°
2
3
°
3*
°
3*
°
3
'
'
'
F3
'
'
'
°
Слайд 21Найдем точку схода этой прямой F4 и перенесем пропорцию на прямую
1-3.
h
k
°
Р
°
S
°
22≡F1
°
F2
h
k1
k2
°
°
°
F1
F2
Р
Р1
°
21≡1
°
21≡1
2
°
22
°
2
3
°
3*
°
3*
°
3
'
'
'
F3
'
'
'
F4
°
°
Слайд 22С помощью точки схода F1 получим перспективы горизонтальных прямых исходного плана
h
k
°
Р
°
S
°
22≡F1
°
F2
h
k1
k2
°
°
°
F1
F2
Р
Р1
°
21≡1
°
21≡1
2
°
22
°
2
3
°
3*
°
3*
°
3
'
'
'
F3
'
'
'
F4
°
°
Слайд 23Завершим построение перспективы плана
h
k
°
Р
°
S
°
22≡F1
°
F2
h
k1
k2
°
°
°
F1
F2
Р
Р1
°
21≡1
°
21≡1
2
°
22
°
2
3
°
3*
°
3*
°
3
'
'
'
F3
'
'
'
F4
°
°
Слайд 24Приступим к построению перспективы объекта. Ребро 1 находится в картине, следовательно
отразится в натуральную величину – по линии связи перенесем его на основание верхней плоскости k1
h
k
°
Р
°
S
°
22≡F1
°
F2
h
k1
k2
°
°
°
F1
F2
Р
Р1
°
21≡1
°
21≡1
2
°
22
°
2
3
°
3*
°
3*
°
3
'
'
'
F3
'
'
'
F4
°
°
Слайд 25Построим перспективы плоскостей, проходящих через ребро 1 в направлении точек схода
F1 и F2
h
k
°
Р
°
S
°
22≡F1
°
F2
h
k1
k2
°
°
°
F1
F2
Р
Р1
°
21≡1
°
21≡1
2
°
22
°
2
3
°
3*
°
3*
°
3
'
'
'
F3
'
'
'
F4
°
°
Слайд 26С помощью опущенного плана произведем «обрезку» плоскостей- поднимем ребра 2 и
3 по линиям связи.
h
k
°
Р
°
S
°
22≡F1
°
F2
h
k1
k2
°
°
°
F1
F2
Р
Р1
°
21≡1
°
21≡1
2
°
22
°
2
3
°
3*
°
3*
°
3
'
'
'
F3
'
'
'
F4
°
°
Слайд 27Завершим построение нижнего основания. Для построения ребер, не касающихся картины, используем
вспомогательную боковую стену
h
k
°
Р
°
S
°
22≡F1
°
F2
h
k1
k2
°
°
°
F1
F2
Р
Р1
°
21≡1
°
21≡1
2
°
22
°
2
3
°
3*
°
3*
°
3
'
'
'
F3
'
'
'
F4
°
°
Слайд 28Применение вспомогательной вертикальной плоскости (боковой стены)
Боковая стена выбирается произвольно
Картинным следом этой
плоскости является ось Оz, а точкой схода ее горизонталей- произвольная точка на линии горизонта
На оси Оz в предметном пространстве откладывают истинные размеры ребер объекта (от (.)О1) и определяют сокращение высоты с помощью (.)схода горизонталей плоскости
На оси Оz в предметном пространстве откладывают истинные размеры ребер объекта (от (.)О1) и определяют сокращение высоты с помощью (.)схода горизонталей плоскости
Слайд 29В произвольном месте поставим ось Z –картинный след вертикальной плоскости и
определим точки О1 и О2 её пересечения с основаниями картины k1 и k2 соответственно.
h
k
°
Р
°
S
°
22≡F1
°
F2
h
k1
k2
°
°
°
F1
F2
Р
Р1
°
21≡1
°
21≡1
2
°
22
°
2
3
°
3*
°
3*
°
3
'
'
'
F3
'
'
'
F4
О1
O2
z
°
°
°
°
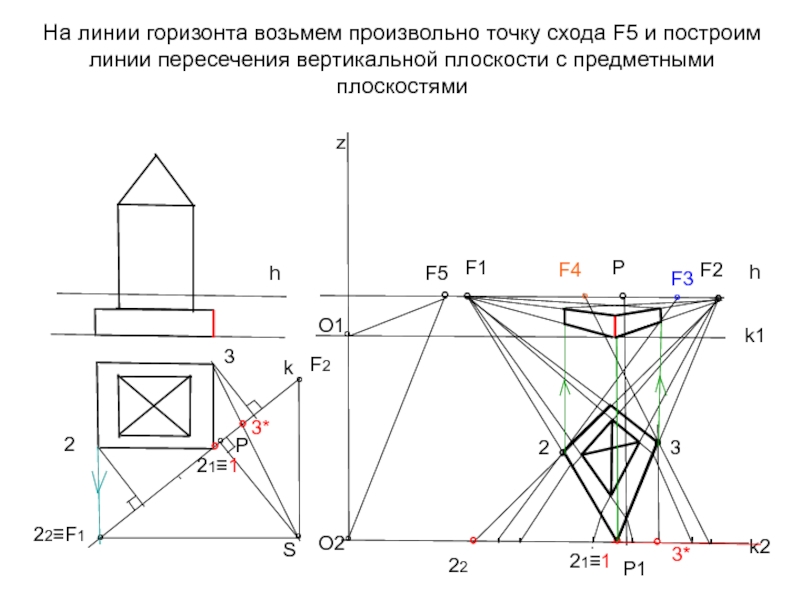
Слайд 30На линии горизонта возьмем произвольно точку схода F5 и построим линии
пересечения вертикальной плоскости с предметными плоскостями
h
k
°
Р
°
S
°
22≡F1
°
F2
h
k1
k2
°
°
°
F1
F2
Р
Р1
°
21≡1
°
21≡1
2
°
22
°
2
3
°
3*
°
3*
°
3
'
'
'
F3
'
'
'
F4
О1
O2
°
F5
z
°
°
°
°
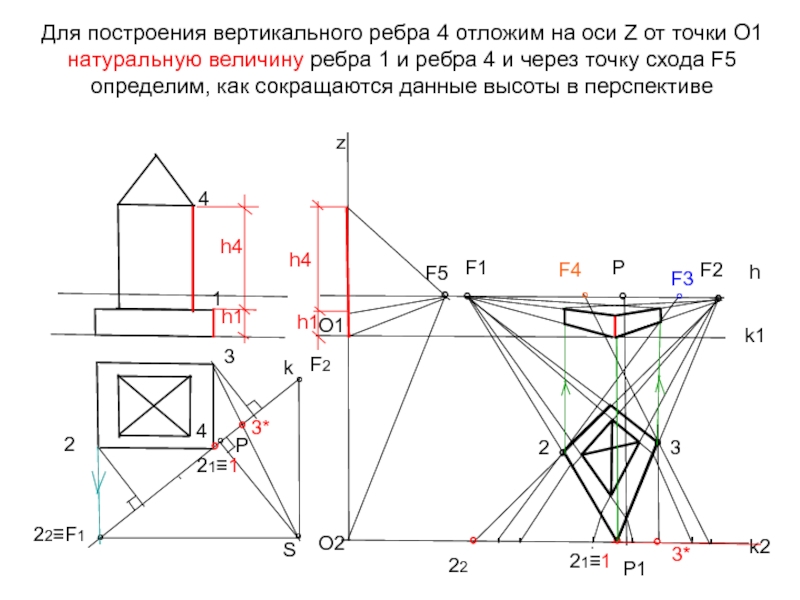
Слайд 31Для построения вертикального ребра 4 отложим на оси Z от точки
О1 натуральную величину ребра 1 и ребра 4 и через точку схода F5 определим, как сокращаются данные высоты в перспективе
h4
k
°
Р
°
S
°
22≡F1
°
F2
h
k1
k2
°
°
°
F1
F2
Р
Р1
°
21≡1
°
21≡1
2
°
22
°
2
3
°
3*
°
3*
°
3
'
'
'
F3
'
'
'
F4
О1
O2
°
F5
z
4
4
1
h4
h1
h1
°
°
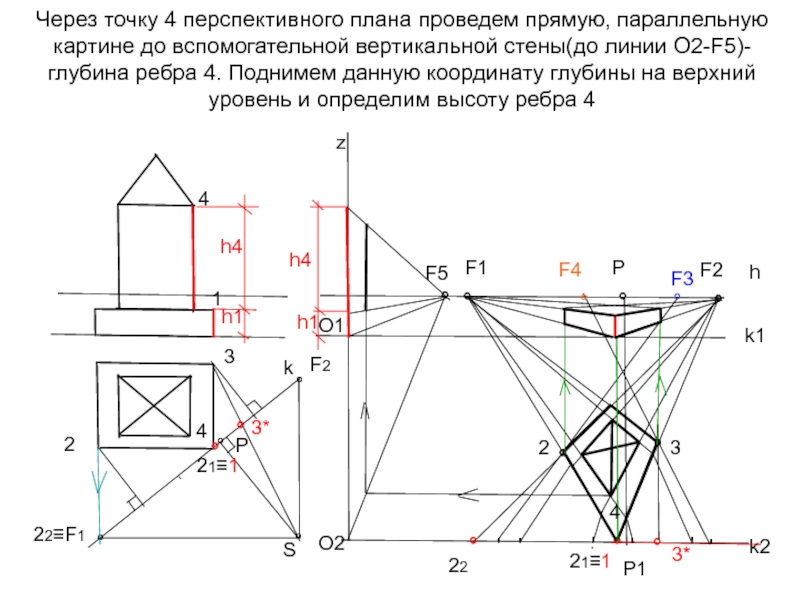
Слайд 32Через точку 4 перспективного плана проведем прямую, параллельную картине до вспомогательной
вертикальной стены(до линии О2-F5)- глубина ребра 4. Поднимем данную координату глубины на верхний уровень и определим высоту ребра 4
h4
k
°
Р
°
S
°
22≡F1
°
F2
h
k1
k2
°
°
°
F1
F2
Р
Р1
°
21≡1
°
21≡1
2
°
22
°
2
3
°
3*
°
3*
°
3
'
'
'
F3
'
'
'
F4
О1
O2
°
F5
z
4
4
1
h4
h1
h1
4
°
°
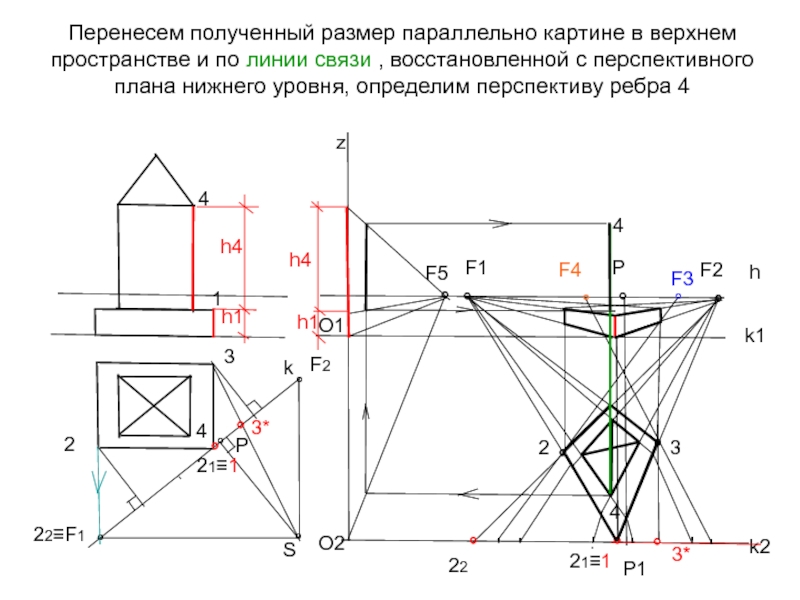
Слайд 33Перенесем полученный размер параллельно картине в верхнем пространстве и по линии
связи , восстановленной с перспективного плана нижнего уровня, определим перспективу ребра 4
h4
k
°
Р
°
S
°
22≡F1
°
F2
h
k1
k2
°
°
°
F1
F2
Р
Р1
°
21≡1
°
21≡1
2
°
22
°
2
3
°
3*
°
3*
°
3
'
'
'
F3
'
'
'
F4
О1
O2
°
F5
z
4
4
1
h4
h1
h1
4
4
°
°
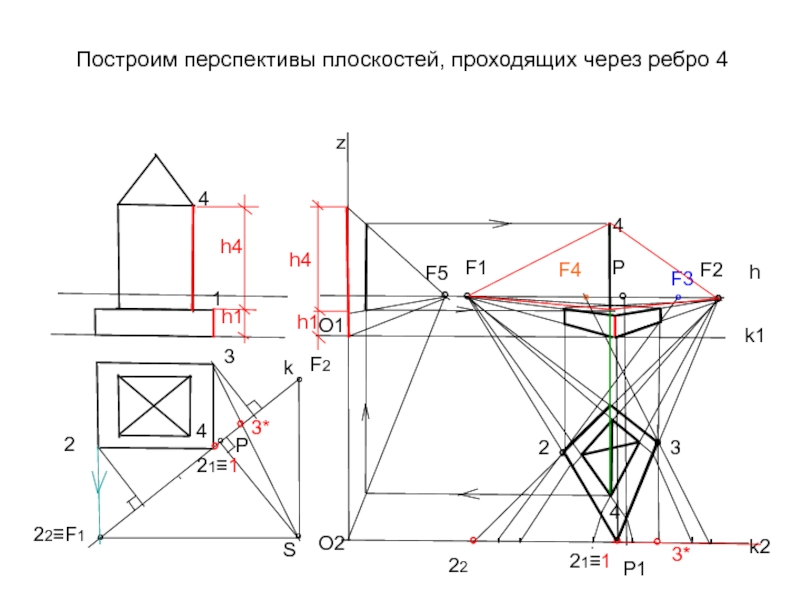
Слайд 34Построим перспективы плоскостей, проходящих через ребро 4
h4
k
°
Р
°
S
°
22≡F1
°
F2
h
k1
k2
°
°
°
F1
F2
Р
Р1
°
21≡1
°
21≡1
2
°
22
°
2
3
°
3*
°
3*
°
3
'
'
'
F3
'
'
'
F4
О1
O2
°
F5
z
4
4
1
h4
h1
h1
4
4
°
°
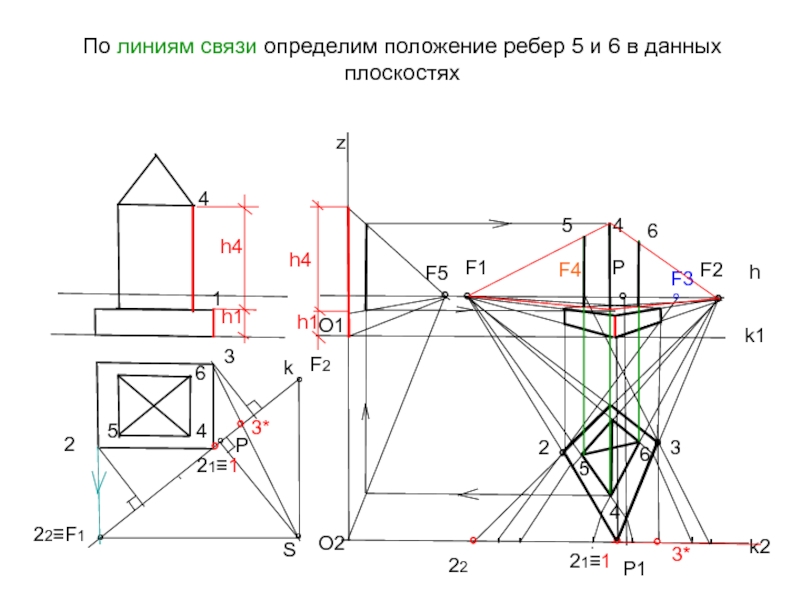
Слайд 35По линиям связи определим положение ребер 5 и 6 в данных
плоскостях
h4
k
°
Р
°
S
°
22≡F1
°
F2
h
k1
k2
°
°
°
F1
F2
Р
Р1
°
21≡1
°
21≡1
2
°
22
°
2
3
°
3*
°
3*
°
3
'
'
'
F3
'
'
'
F4
О1
O2
°
F5
z
4
4
1
h4
h1
h1
4
4
5
5
6
6
5
6
°
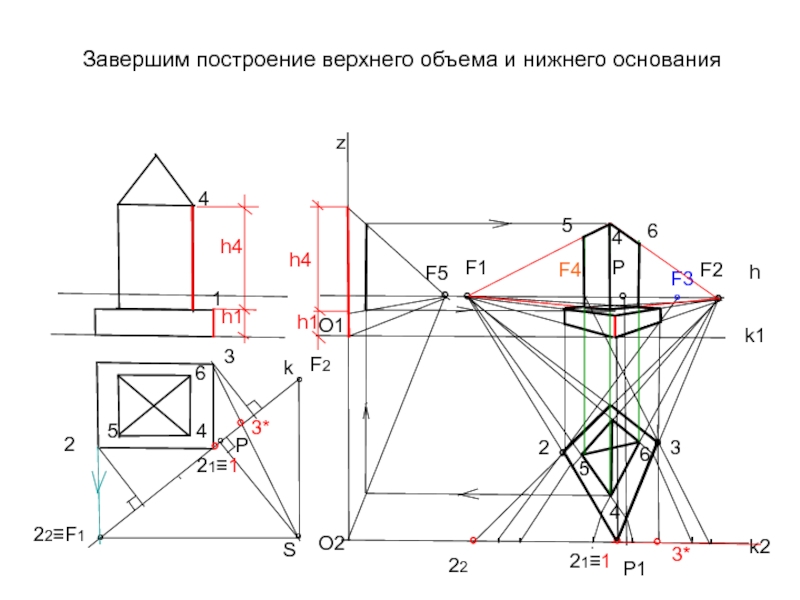
Слайд 36Завершим построение верхнего объема и нижнего основания
h4
k
°
Р
°
S
°
22≡F1
°
F2
h
k1
k2
°
°
°
F1
F2
Р
Р1
°
21≡1
°
21≡1
2
°
22
°
2
3
°
3*
°
3*
°
3
'
'
'
F3
'
'
'
F4
О1
O2
°
F5
z
4
4
1
h4
h1
h1
4
4
5
5
6
6
5
6
°
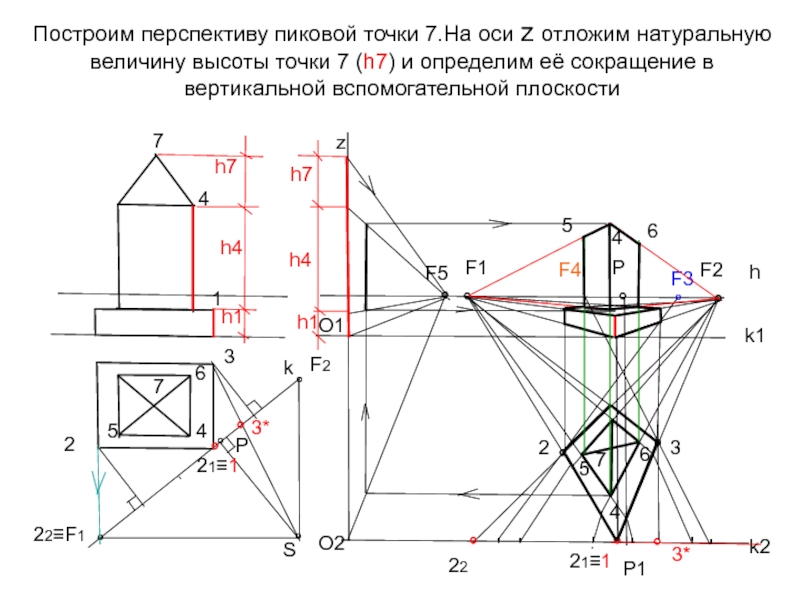
Слайд 37Построим перспективу пиковой точки 7.На оси z отложим натуральную величину высоты
точки 7 (h7) и определим её сокращение в вертикальной вспомогательной плоскости
h4
k
°
Р
°
S
°
22≡F1
°
F2
h
k1
k2
°
°
°
F1
F2
Р
Р1
°
21≡1
°
21≡1
2
°
22
°
2
3
°
3*
°
3*
°
3
'
'
'
F3
'
'
'
F4
О1
O2
°
F5
z
4
4
1
h4
h1
h1
4
4
5
5
6
6
5
6
7
7
7
h7
h7
°
Слайд 38Через точку 7 перспективного плана проведем прямую, параллельную картине до вспомогательной
вертикальной стены (до линии О2-F5)- определяем глубину точки 7. Поднимем данную координату глубины на верхний уровень и определим высоту точки 7 на данной глубине
h4
k
°
Р
°
S
°
22≡F1
°
F2
h
k1
k2
°
°
°
F1
F2
Р
Р1
°
21≡1
°
21≡1
2
°
22
°
2
3
°
3*
°
3*
°
3
'
'
'
F3
'
'
'
F4
О1
O2
°
F5
z
4
4
1
h4
h1
h1
4
4
5
5
6
6
5
6
7
7
7
h7
h7
°
°
Слайд 39Перенесем полученный размер параллельно картине в верхнем пространстве и по линии
связи , восстановленной с перспективного плана нижнего уровня, определим перспективу точки 7
h4
k
°
Р
°
S
°
22≡F1
°
F2
h
k1
k2
°
°
°
F1
F2
Р
Р1
°
21≡1
°
21≡1
2
°
22
°
2
3
°
3*
°
3*
°
3
'
'
'
F3
'
'
'
F4
О1
O2
°
F5
z
4
4
1
h4
h1
h1
4
4
5
5
6
6
5
6
7
7
7
h7
h7
°
7
°
°
Слайд 40Завершим построение кровли объекта
h4
k
°
Р
°
S
°
22≡F1
°
F2
h
k1
k2
°
°
°
F1
F2
Р
Р1
°
21≡1
°
21≡1
2
°
22
°
2
3
°
3*
°
3*
°
3
'
'
'
F3
'
'
'
F4
О1
O2
°
F5
z
4
4
1
h4
h1
h1
4
4
5
5
6
6
5
6
7
7
7
h7
h7
°
7
°
°
