- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Положение прямой относительно плоскостей проекций презентация
Содержание
Слайд 2
α
β
A1
B1
A
A2
Ax
B
B2
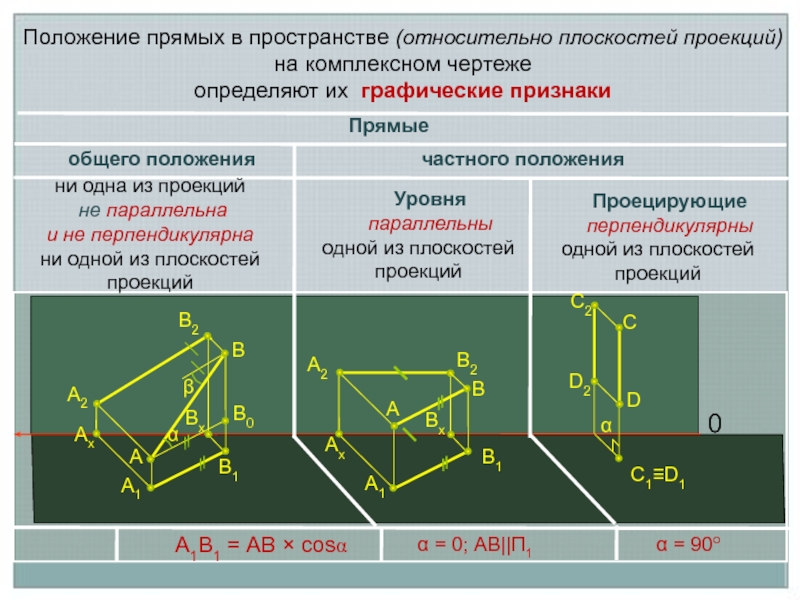
α = 0; АВ||П1
A1
B1
A
A2
Ax
C
C2
0
B
B2
D
D2
C1≡D1
α = 90o
А1В1 = АВ × cosα
Положение прямых в пространстве (относительно плоскостей проекций)
на комплексном чертеже
определяют их графические признаки
Прямые
общего положения частного положения
Уровня
параллельны одной из плоскостей проекций
Проецирующие
перпендикулярны одной из плоскостей проекций
Вx
Вx
B0
ни одна из проекций
не параллельна
и не перпендикулярна
ни одной из плоскостей
проекций
α
Слайд 4
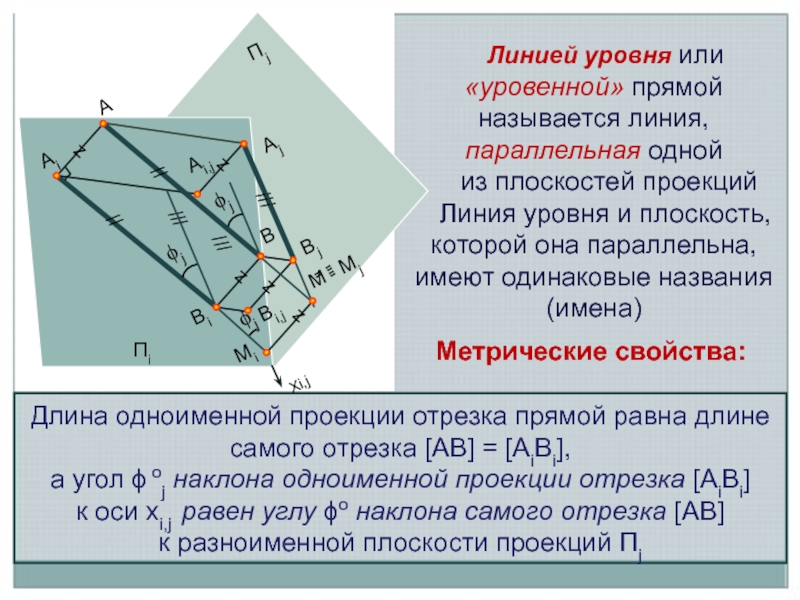
Линией уровня или «уровенной» прямой называется линия, параллельная одной
из
Линия уровня и плоскость, которой она параллельна, имеют одинаковые названия (имена)
Метрические свойства:
Длина одноименной проекции отрезка прямой равна длине самого отрезка [АВ] = [АiВi],
а угол ϕ оj наклона одноименной проекции отрезка [АiВi]
к оси хi,j равен углу ϕо наклона самого отрезка [АВ]
к разноименной плоскости проекций Πj
Пi
Пj
Xi,j
Aj
Ai
B
Bi
A
Bj
//
///
z
z
ϕj
М Мj
ппп
//
///
z
z
z
ϕj
///
ϕj
Мi
Bi,j
Ai,j
Слайд 5
h2
h3
h1=нв[h]
П1
П2
Х1,2
Zh
Zh
Zh
Zh
П3
Z(х2,3)
Y(х1,3)
Y(х1,3)
h – горизонталь
ϕ3
ϕ2
h2
h1
h3
h
z(х2,3)
y(х1,3)
x1,2
Слайд 6
f1
f2=нв[f]
Х1,2
yf
П3
Z(х2,3)
Y(х1,3)
f – фронталь
yf
yf
yf
f3
ϕ1
ϕ3
Y(х1,3)
П2
П1
f3
f1
f2
f
x1,2
y(х1,3)
z(х2,3)
П3
П2
П1
//
//
Слайд 7
р – профильная прямая
р1
р3=нв[р]
Х1,2
П3
Z(Х2,3)
Y(Х1,3)
yf
yр
р3
ϕ1
ϕ3
Y(Х1,3)
р2
хр
хр
П2
П1
хр
хр
yр
р2
р3
р1
р
z(х2,3)
y(х1,3)
x1,2
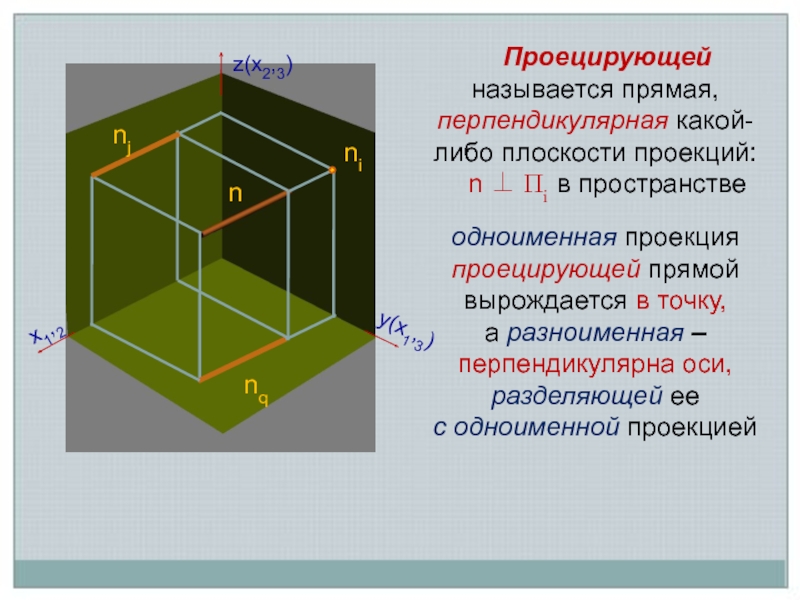
Слайд 8Проецирующей называется прямая, перпендикулярная какой-либо плоскости проекций:
n ⊥ Пi в
n
nj
ni
nq
одноименная проекция проецирующей прямой вырождается в точку,
а разноименная – перпендикулярна оси, разделяющей ее
с одноименной проекцией
x1,2
y(х1,3)
z(х2,3)
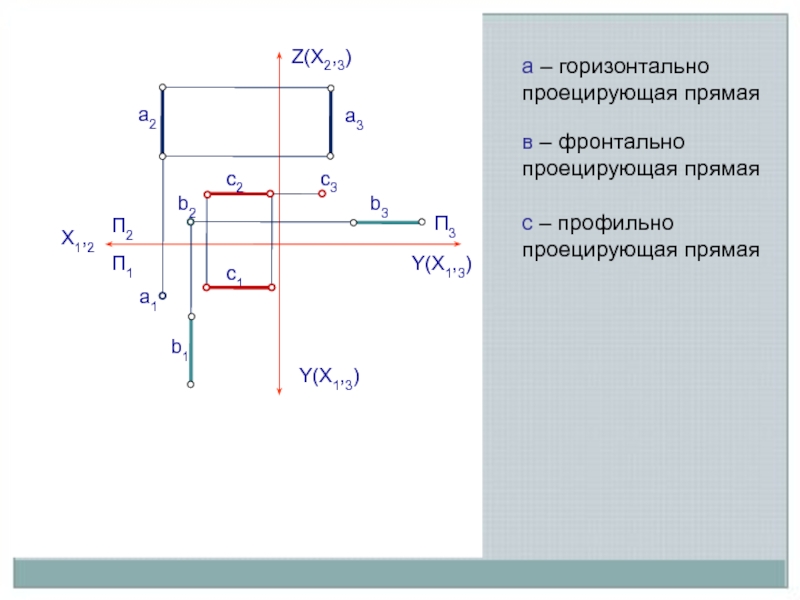
Слайд 9
а – горизонтально проецирующая прямая
в – фронтально проецирующая прямая
с – профильно
Х1,2
П3
Z(Х2,3)
Y(Х1,3)
Y(Х1,3)
П2
П1
а2
а1
а3
b2
b3
b1
c2
c1
c3
