- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Положение плоскости относительно плоскостей проекций презентация
Содержание
Плоскости частного положения
Слайд 3Плоскость, перпендикулярная к плоскости проекций, называется проецирующей
Особенности
проецирующих плоскостей:
– одна проекция
любого элемента, расположенного
– в проецирующей плоскости, совпадает
с соответствующим следом этой плоскости
– в проецирующей плоскости, совпадает
с соответствующим следом этой плоскости
– угол наклона заданной плоскости к плоскости проекций на эпюре проецируется в натуральную величину
Проецирующие плоскости
Слайд 4
х
А2
В2
С2
С1
А1
В1
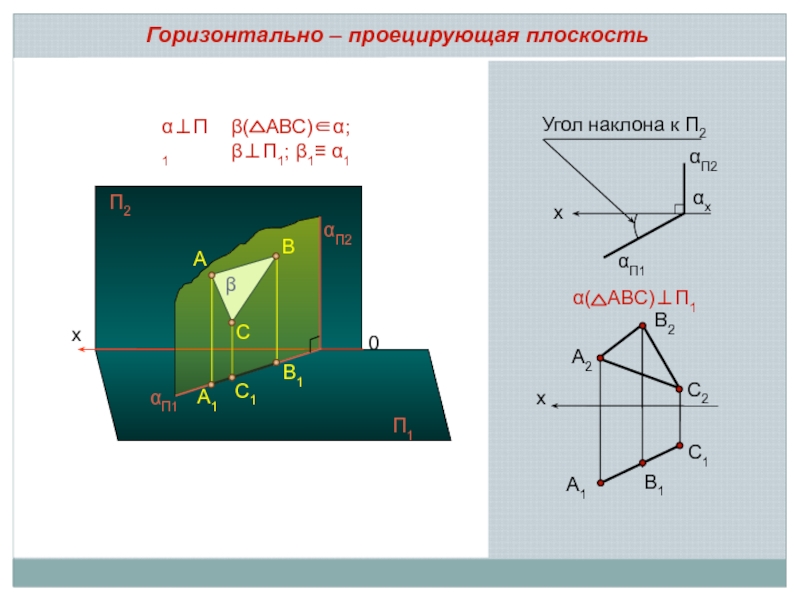
α( АВС)⊥П1
Горизонтально – проецирующая плоскость
x
αП1
αx
Угол наклона к П2
x
A1
B1
A
0
B
C
αП2
С1
П2
П1
α⊥П1
β
β( АВС)∈α; β⊥П1; β1≡ α1
αП1
αП2
Слайд 5
x
A2
B2
A
0
B
C
βП2
βП1
С2
П2
П1
β⊥П2
δ
δ( АВС)∈β;
β⊥П2; β2≡δ2
х
А2
В2
С2
С1
А1
В1
β( АВС)⊥П2
x
βП1
βП2
βx
Угол наклона к П1
Фронтально – проецирующая плоскость
δ2
Слайд 6
x
A
0
B
C
γП2
γП1
П2
П1
A3
С1
B1
П3
α
х
А3
В3
С3
С1
А1
В1
В2
А2
С2
γ( АВС)⊥П3
Профильно
– проецирующая плоскость
z
y
x
γП1
γП2
γП3
z
у
у
ϕ
β
∠ϕ=γ∧П2
∠β=γ∧П1
γП3
α3
γ⊥П3; α( АВС)⊥ П3; γП3≡α3
ϕ
β
Слайд 7Плоскость,
параллельная к плоскости проекций, называется плоскостью уровня
Особенности
плоскостей уровня:
Плоскости уровня
– любая
плоская фигура,
расположенная в плоскости уровня,
проецируется на параллельную ей плоскость проекций без искажения, – т.е. в натуральную величину
расположенная в плоскости уровня,
проецируется на параллельную ей плоскость проекций без искажения, – т.е. в натуральную величину
Слайд 8
АВС||П1⇒ А1В1С1=| АВС|
A1
B1
A
A2
Ax
0
B
B2
αllП1
С1
С2
α
Горизонтальная плоскость
П2
П1
АВС∈α;
АВС ll П1
АВС ll А1В1С1
С
Слайд 9
Плоскости уровня
х
А2
В2
С2
С1
А1
В1
х
А2
В2
С2
С1
А1
В1
х
А3
В3
С3
С1
А1
В1
//
//
α( АВС) ll П1
Натуральная величина
//
//
нв
β( АВС) ll П2
В2
А2
С2
//
//
//
//
γ(
АВС) ll П3
нв
горизонтальная
фронтальная
профильная
z
y
