- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Перспектива. Общие сведения презентация
Содержание
- 1. Перспектива. Общие сведения
- 2. использован материал Вольхина К.А. по НГ и
- 3. использован материал Вольхина К.А. по НГ и
- 4. использован материал Вольхина К.А. по НГ и
- 5. использован материал Вольхина К.А. по НГ и
- 6. использован материал Вольхина К.А. по НГ и
- 7. использован материал Вольхина К.А. по НГ и
- 8. использован материал Вольхина К.А. по НГ и
- 9. использован материал Вольхина К.А. по НГ и
- 10. использован материал Вольхина К.А. по НГ и
- 11. использован материал Вольхина К.А. по НГ и
- 12. использован материал Вольхина К.А. по НГ и
- 13. использован материал Вольхина К.А. по НГ и
- 14. использован материал Вольхина К.А. по НГ и
- 15. использован материал Вольхина К.А. по НГ и
- 16. использован материал Вольхина К.А. по НГ и
- 17. использован материал Вольхина К.А. по НГ и
- 18. использован материал Вольхина К.А. по НГ и
- 19. использован материал Вольхина К.А. по НГ и
- 20. использован материал Вольхина К.А. по НГ и
- 21. использован материал Вольхина К.А. по НГ и
- 22. использован материал Вольхина К.А. по НГ и
- 23. использован материал Вольхина К.А. по НГ и
- 24. использован материал Вольхина К.А. по НГ и
- 25. использован материал Вольхина К.А. по НГ и
- 26. использован материал Вольхина К.А. по НГ и
- 27. использован материал Вольхина К.А. по НГ и
- 28. использован материал Вольхина К.А. по НГ и
- 29. использован материал Вольхина К.А. по НГ и
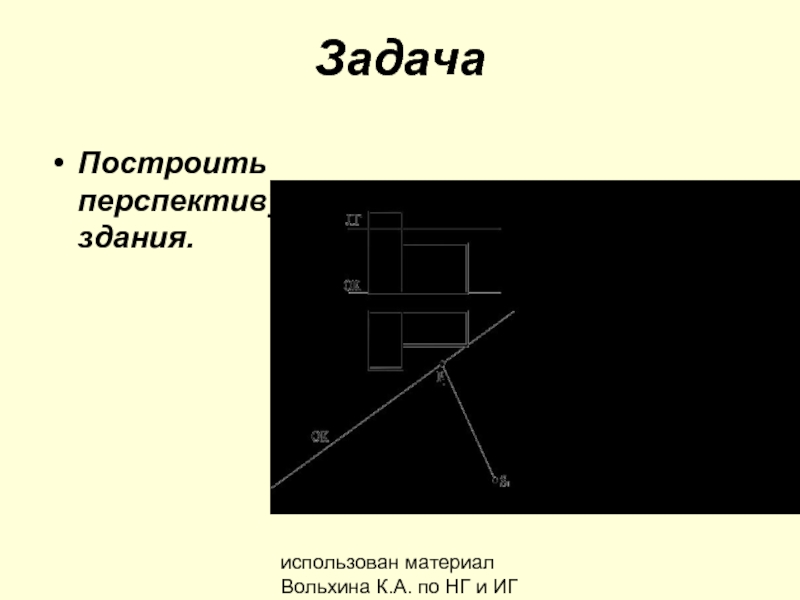
- 30. использован материал Вольхина К.А. по НГ и ИГ Задача Построить перспективу здания.
Слайд 1использован материал Вольхина К.А. по НГ и ИГ
Лекция 10. ПЕРСПЕКТИВА.
ОБЩИЕ
Перспективой (перспективной проекцией) называется центральная проекция предмета на специально выбранную поверхность.
Перспектива происходит от латинского глагола "perspicere" − видеть насквозь.
Перспектива является одним из методов построения наглядных изображений пространственных предметов, которые широко используются в инженерной графике и особенно в архитектурно-строительном черчении.
Слайд 2использован материал Вольхина К.А. по НГ и ИГ
В зависимости от вида
Линейная перспектива − проецирование на вертикальную плоскость.
Плафонная перспектива − проецирование на горизонтальную плоскость.
Панорамная перспектива − проецирование на цилиндрическую поверхность.
Купольная перспектива − проецирование на сферу.
Слайд 3использован материал Вольхина К.А. по НГ и ИГ
ЛИНЕЙНАЯ ПЕРСПЕКТИВА
Ограничимся рассмотрением только
Построение перспективы предмета из некоторой точки (точки зрения) осуществляется в следующей последовательности:
1. Из точки проводим лучи ко всем точкам предмета.
2. На пути проецирующих лучей располагаем плоскость.
3. Точки пересечения лучей с плоскостью определяют искомое изображение.
Слайд 4использован материал Вольхина К.А. по НГ и ИГ
ОСНОВНЫЕ ПОНЯТИЯ И ОБОЗНАЧЕНИЯ
Горизонтальная плоскость
Центр проецирования S, т.е. точка, в которой располагается глаз наблюдателя, называется точкой зрения.
Слайд 5использован материал Вольхина К.А. по НГ и ИГ
Горизонтальные проекции точек, т.е.
S1 − основание точки зрения или точка стояния.
ОК − линия пересечения картинной и предметной плоскостей называется основанием картинной плоскости или основанием картины.
Слайд 6использован материал Вольхина К.А. по НГ и ИГ
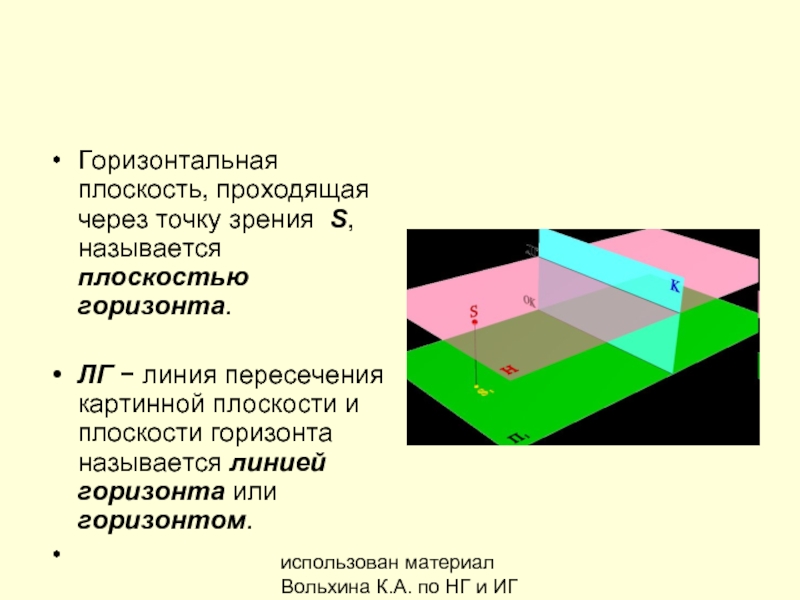
Горизонтальная плоскость, проходящая через
ЛГ − линия пересечения картинной плоскости и плоскости горизонта называется линией горизонта или горизонтом.
Слайд 7использован материал Вольхина К.А. по НГ и ИГ
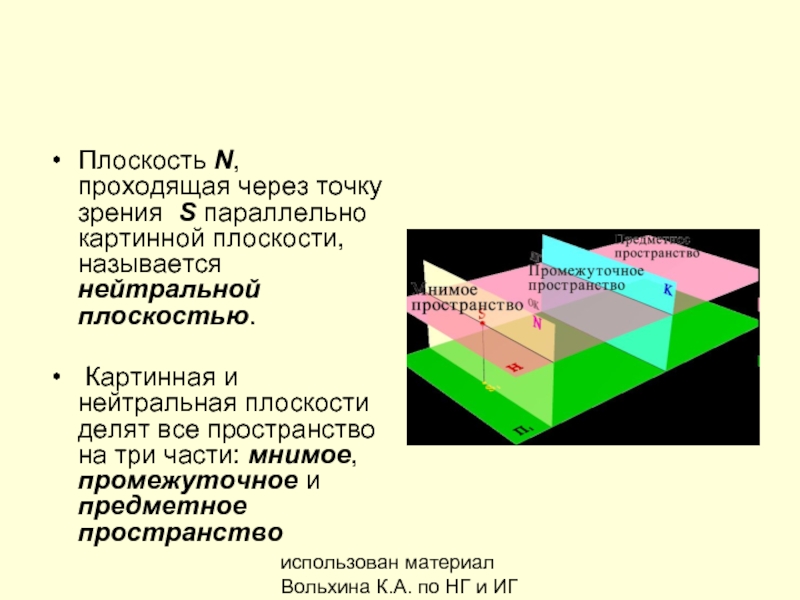
Плоскость N, проходящая через
Картинная и нейтральная плоскости делят все пространство на три части: мнимое, промежуточное и предметное пространство
Слайд 8использован материал Вольхина К.А. по НГ и ИГ
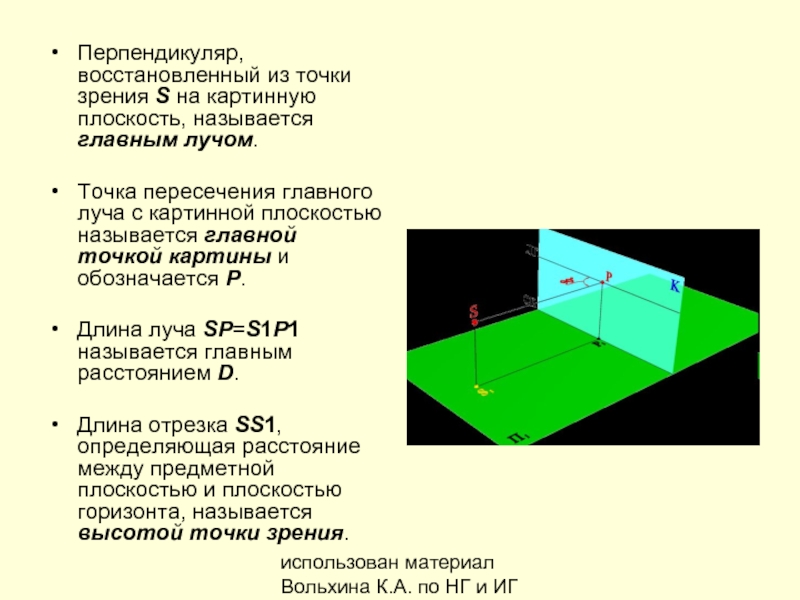
Перпендикуляр, восстановленный из точки
Точка пересечения главного луча с картинной плоскостью называется главной точкой картины и обозначается Р.
Длина луча SP=S1P1 называется главным расстоянием D.
Длина отрезка SS1, определяющая расстояние между предметной плоскостью и плоскостью горизонта, называется высотой точки зрения.
Слайд 9использован материал Вольхина К.А. по НГ и ИГ
ПЕРСПЕКТИВА ТОЧКИ
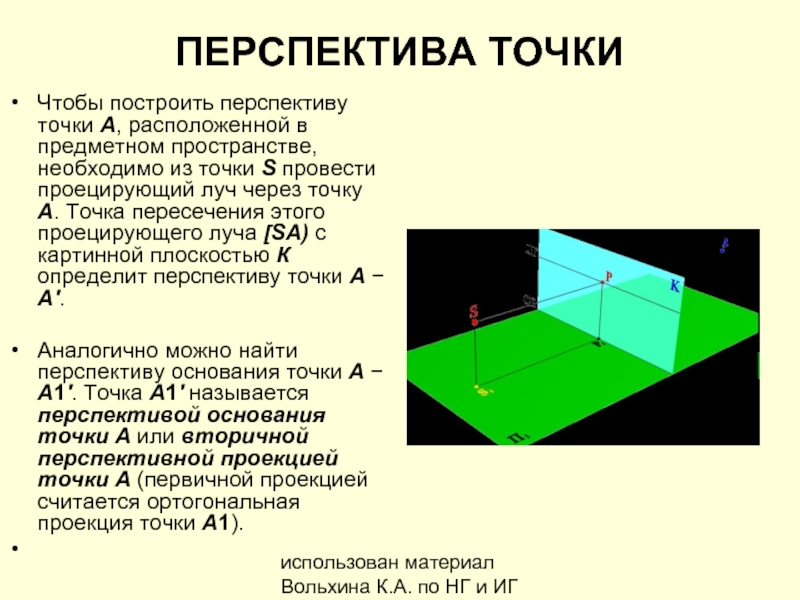
Чтобы построить перспективу
Аналогично можно найти перспективу основания точки А − A1'. Точка A1' называется перспективой основания точки А или вторичной перспективной проекцией точки А (первичной проекцией считается ортогональная проекция точки А1).
Слайд 10использован материал Вольхина К.А. по НГ и ИГ
При рассмотрении центрального проецирования
Правило 1. Перспектива точки и перспектива основания этой точки лежат на прямой, перпендикулярной основанию картины.
Слайд 11использован материал Вольхина К.А. по НГ и ИГ
ПЕРСПЕКТИВА ПРЯМЫХ ОБЩЕГО ПОЛОЖЕНИЯ
На
Правило 2. Перспектива прямой есть прямая.
Слайд 12использован материал Вольхина К.А. по НГ и ИГ
Правило 3.
Перспективу прямой
Слайд 13использован материал Вольхина К.А. по НГ и ИГ
Правило 4.
Перспективы параллельных
Слайд 14использован материал Вольхина К.А. по НГ и ИГ
ПЕРСПЕКТИВЫ ГОРИЗОНТАЛЬНЫХ ПРЯМЫХ
Горизонтальные прямые
Правило 5. Точки схода горизонтальных прямых принадлежат линии горизонта.
Слайд 15использован материал Вольхина К.А. по НГ и ИГ
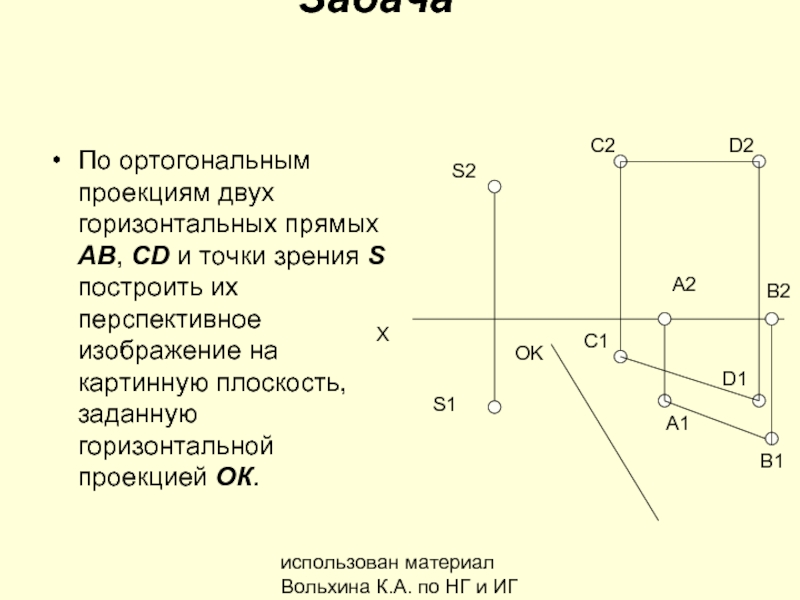
Задача
По ортогональным проекциям двух
B1
B2
Слайд 16использован материал Вольхина К.А. по НГ и ИГ
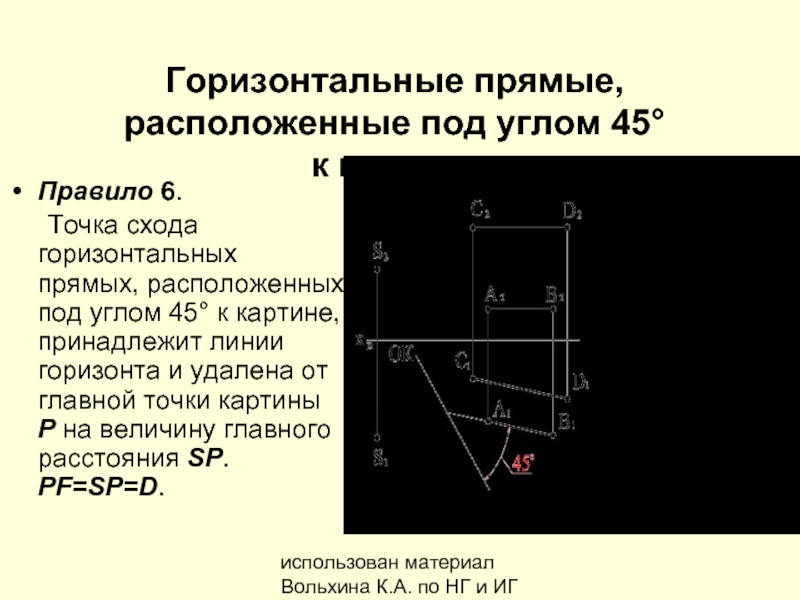
Горизонтальные прямые, расположенные под
Правило 6.
Точка схода горизонтальных прямых, расположенных под углом 45° к картине, принадлежит линии горизонта и удалена от главной точки картины Р на величину главного расстояния SP. PF=SP=D.
Слайд 17использован материал Вольхина К.А. по НГ и ИГ
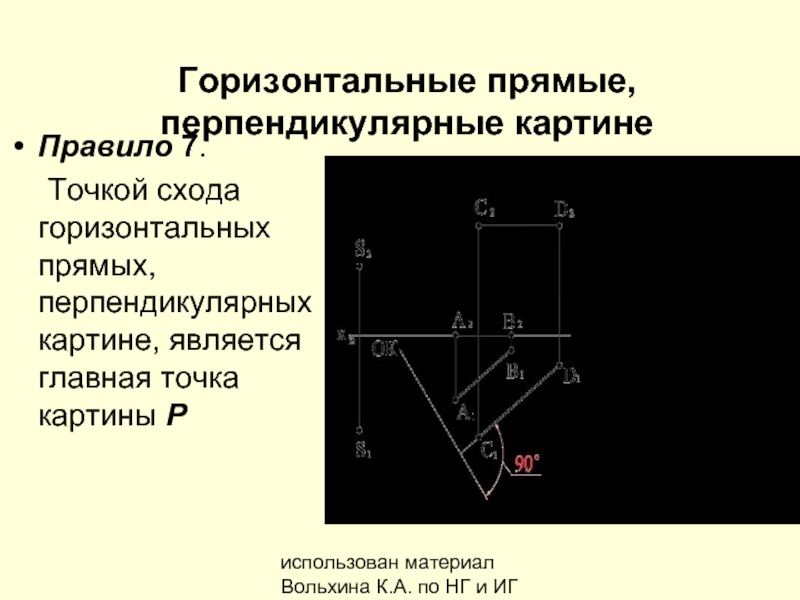
Горизонтальные прямые, перпендикулярные картине
Правило
Точкой схода горизонтальных прямых, перпендикулярных картине, является главная точка картины Р
Слайд 18использован материал Вольхина К.А. по НГ и ИГ
Горизонтальные прямые, проходящие через
Правило 8. Перспективы прямых, принадлежащих предметной плоскости П1 и проходящих через основание точки зрения, перпендикулярны основанию картины ОК и линии горизонта ЛГ.
Слайд 19использован материал Вольхина К.А. по НГ и ИГ
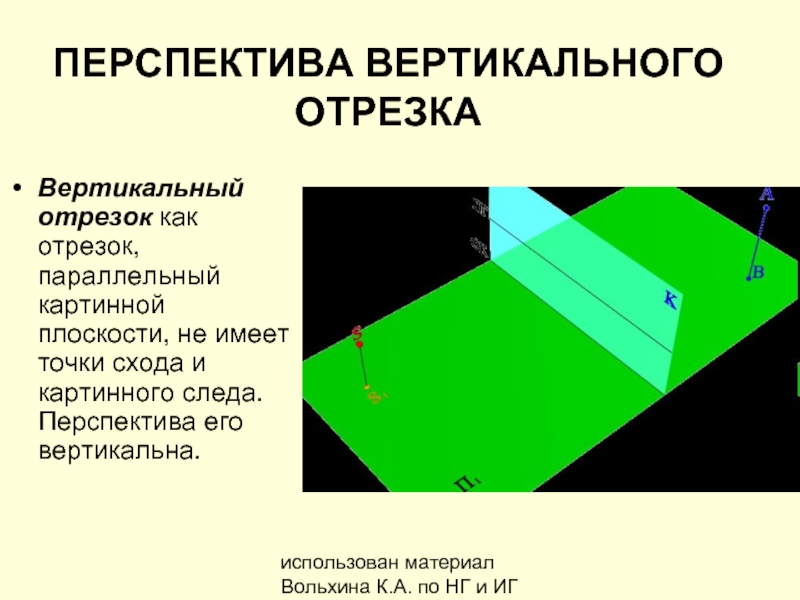
ПЕРСПЕКТИВА ВЕРТИКАЛЬНОГО ОТРЕЗКА
Вертикальный отрезок
Слайд 20использован материал Вольхина К.А. по НГ и ИГ
ПОСТРОЕНИЕ ПЕРСПЕКТИВЫ ТОЧКИ
Точку в
Построение перспективы можно выполнять с использованием одной или двух точек схода.
Слайд 21использован материал Вольхина К.А. по НГ и ИГ
ДЕЛЕНИЕ ПЕРСПЕКТИВЫ ОТРЕЗКОВ ПРЯМЫХ
Чтобы разделить отрезок прямой в заданном соотношении, используется теорема Фалеса.
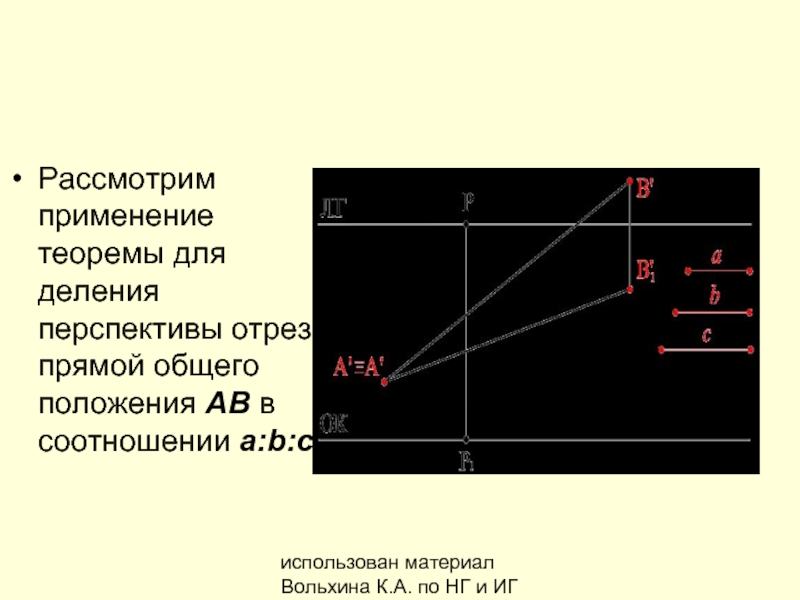
Рассмотрим применение этой теоремы для деления перспективы отрезка АВ, расположенного в предметной плоскости в соотношении а:b:с.
Слайд 22использован материал Вольхина К.А. по НГ и ИГ
Рассмотрим применение теоремы для
Слайд 23использован материал Вольхина К.А. по НГ и ИГ
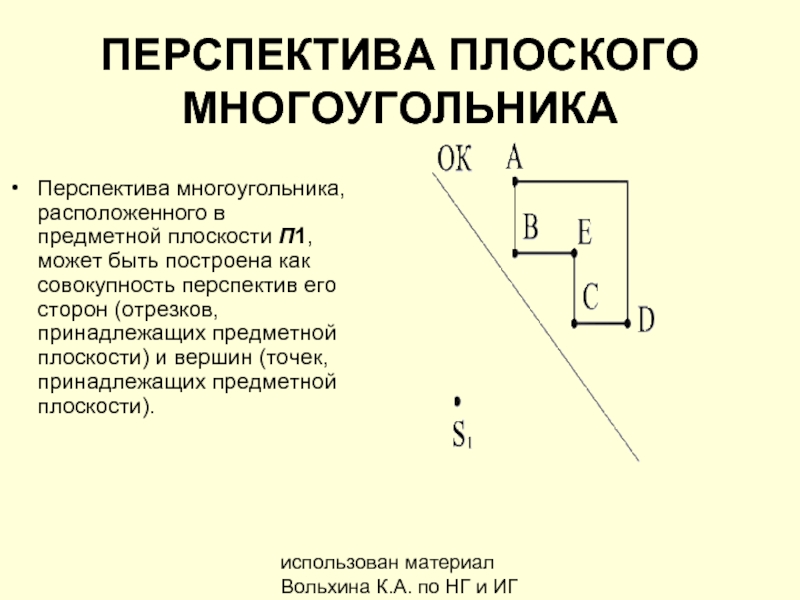
ПЕРСПЕКТИВА ПЛОСКОГО МНОГОУГОЛЬНИКА
Перспектива многоугольника,
Слайд 24использован материал Вольхина К.А. по НГ и ИГ
ПЕРСПЕКТИВА ОКРУЖНОСТИ
Перспектива окружности строится
Фиксируем положение ряда точек окружности пересекающимися прямыми частного положения.
Строим перспективы этих прямых и отмечаем точки их пересечения − искомые перспективы точек окружности.
Слайд 25использован материал Вольхина К.А. по НГ и ИГ
ВЫБОР РАЦИОНАЛЬНОГО ПОЛОЖЕНИЯ ТОЧКИ
Чтобы обеспечить удачное перспективное изображение предмета, рекомендуется руководствоваться следующими правилами, выработанными практикой:
1. Реальность точки зрения. Она должна выбираться с учетом существующей или запроектированной ситуации. Точка зрения должна выбираться на таком расстоянии от объекта, чтобы его можно было легко охватить взглядом.
2. Горизонтальные углы зрения a между крайними лучами в плане должны находиться в пределах от 20° до 50°. Горизонтальный угол 50° − это предельно большая величина угла зрения. Лучшими углами следует считать углы 30° − 40°.
Слайд 26использован материал Вольхина К.А. по НГ и ИГ
3. Если изображается высотное здание,
Для этого следует провести в плане проецирующий луч S к ближайшему вертикальному ребру, а затем повернуть его вместе с точкой зрения во фронтальное положение, спроецировать на фасад, на линию горизонта. Из полученной точки S2' надо провести луч к верхней точке ребра здания и проверить величину угла. Вертикальный угол зрения удобно отсчитывать от перпендикуляра, проведенного к картине, т.е. от главного луча. Это половина полного угла зрения. Вертикальный угол зрения φ' не должен превышать 40°.
Слайд 27использован материал Вольхина К.А. по НГ и ИГ
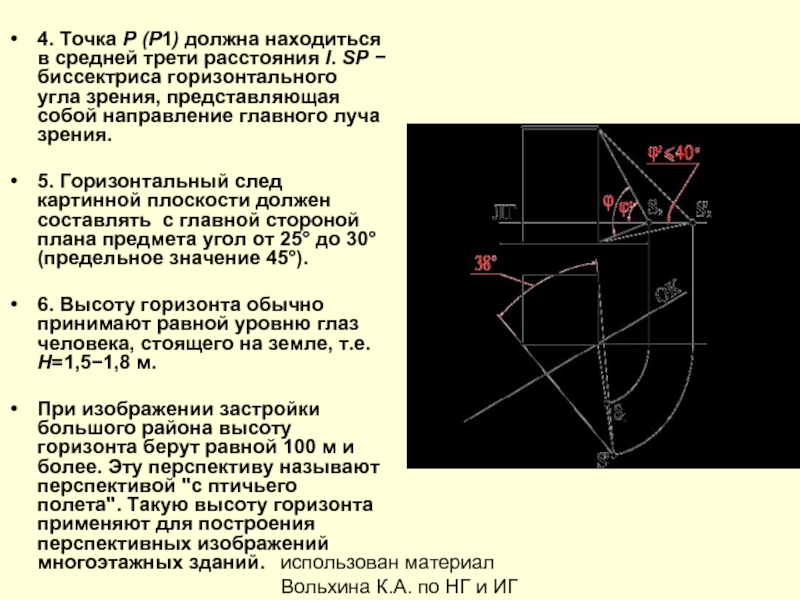
4. Точка Р (Р1) должна
5. Горизонтальный след картинной плоскости должен составлять с главной стороной плана предмета угол от 25° до 30°(предельное значение 45°).
6. Высоту горизонта обычно принимают равной уровню глаз человека, стоящего на земле, т.е. Н=1,5−1,8 м.
При изображении застройки большого района высоту горизонта берут равной 100 м и более. Эту перспективу называют перспективой "с птичьего полета". Такую высоту горизонта применяют для построения перспективных изображений многоэтажных зданий.
Слайд 28использован материал Вольхина К.А. по НГ и ИГ
СПОСОБЫ ПОСТРОЕНИЯ ПЕРСПЕКТИВЫ ГЕОМЕТРИЧЕСКИХ
1. Способ архитекторов. В основу этого способа положено свойство перспективных проекций параллельных прямых, которое заключается в том, что они сходятся в одной точке (имеют общую точку схода F).
2. Радиальный способ заключается в том, что перспектива любой точки определяется как след луча зрения (т.е. как точка пересечения луча зрения, проходящего через заданную точку, с картинной плоскостью). Способ разработан немецким художником, математиком и гравером Альбертом Дюрером (1471 − 1528) и поэтому иногда называется способом Дюрера.
3. Способ сетки. Способ построения перспективы с помощью сетки заключается в том, что предварительно на ортогональных проекциях наносят равномерную ортогональную сетку, а затем строят перспективное изображение этой сетки.
Слайд 29использован материал Вольхина К.А. по НГ и ИГ
ПОСТРОЕНИЕ ПЕРСПЕКТИВЫ ОБЪЕКТА СПОСОБОМ
В практике построения перспектив наибольшее распространение получил способ архитекторов.
Этот способ применяется при построении перспективных изображений различных сооружений, которые в плане имеют два доминирующих направления линий (например, здания, мосты, путепроводы).
Использование двух точек схода перспектив параллельных горизонтальных прямых объекта доминирующих направлений обеспечивает большую графическую точность и простоту построения перспективного изображения.