- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Образование комплексного чертежа презентация
Содержание
O – Origo начало O X Z Y I II III IV V VI VII VIII Пространственная модель координатных плоскостей проекций Плоскости проекций в Декартовой
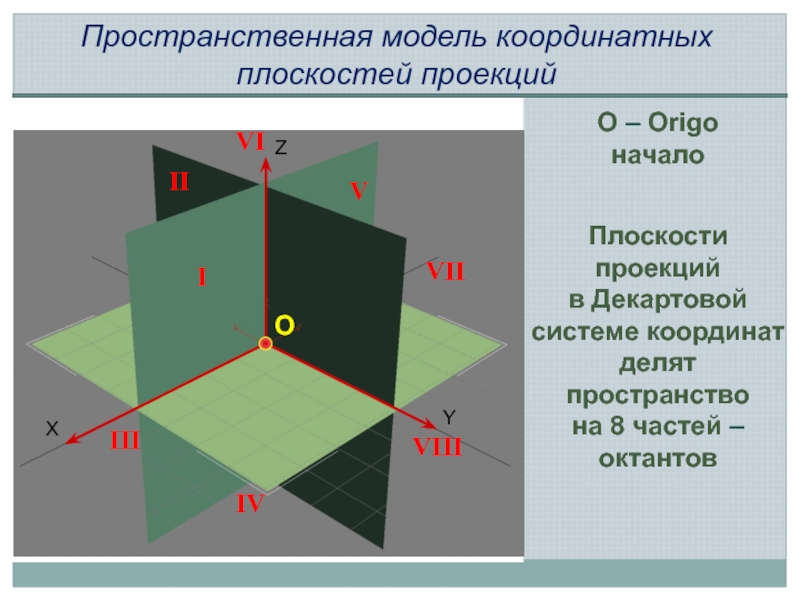
Слайд 2O – Origo начало
O
X
Z
Y
I
II
III
IV
V
VI
VII
VIII
Пространственная модель координатных плоскостей проекций
Плоскости проекций
в Декартовой
системе координат делят пространство
на 8 частей – октантов
на 8 частей – октантов
Слайд 3
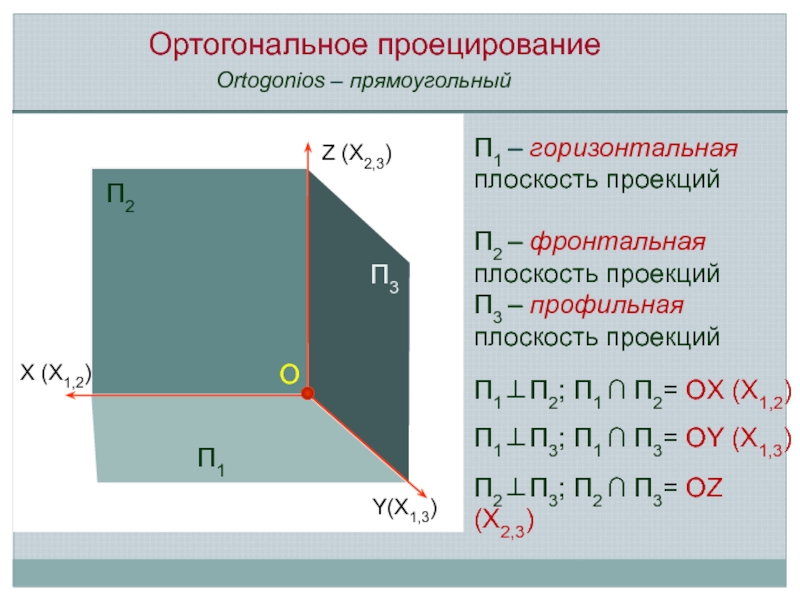
Ортогональное проецирование
П2
П1
П3
П1 – горизонтальная плоскость проекций
П2 – фронтальная плоскость проекций
П3 –
профильная плоскость проекций
П1⊥П2; П1 ∩ П2= OX (X1,2)
П1⊥П3; П1 ∩ П3= OY (X1,3)
П2⊥П3; П2 ∩ П3= OZ (X2,3)
Z (Х2,3)
Y(Х1,3)
О
Ortogonios – прямоугольный
Х (Х1,2)
Слайд 4
А
П2
П1
П3
X
Z
Y
O
А2
А1
АZ
А3
АY
АX
XА
XА
XА
XА
ZА
ZА
ZА
ZА
YА
YА
YА
YА
//
//
//
//
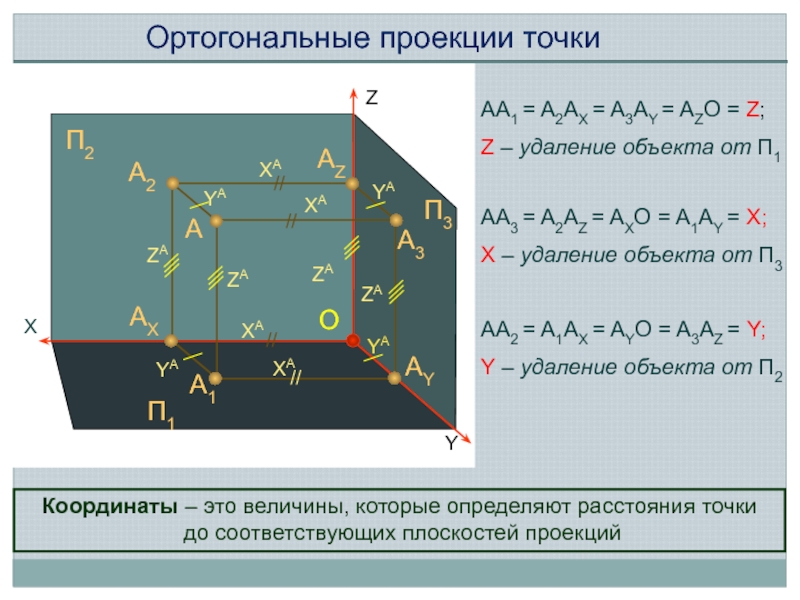
AA1 = A2AX = A3AY = AZO = Z;
Z –
удаление объекта от П1
AA3 = A2AZ = AXO = A1AY = X;
X – удаление объекта от П3
AA2 = A1AX = AYO = A3AZ = Y;
Y – удаление объекта от П2
Ортогональные проекции точки
Координаты – это величины, которые определяют расстояния точки
до соответствующих плоскостей проекций
Слайд 6
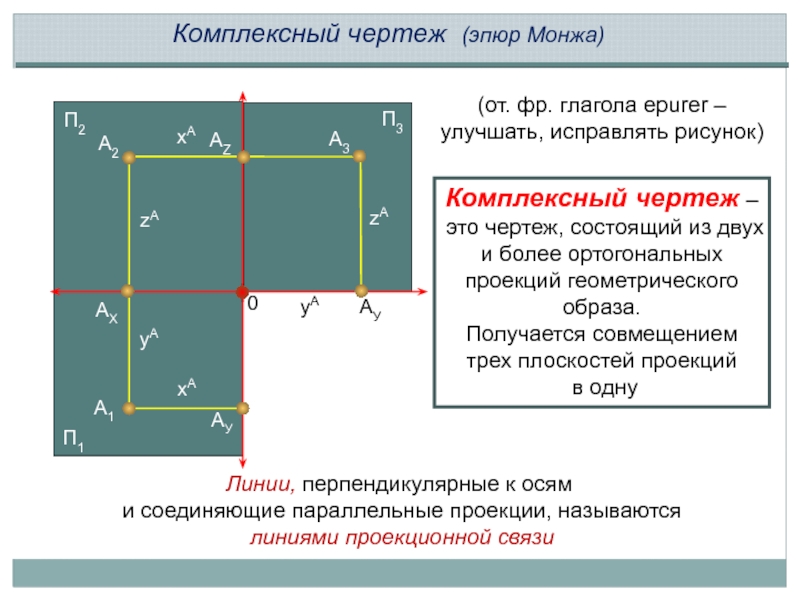
Комплексный чертеж (эпюр Монжа)
А1
А2
А3
zA
zA
xA
xA
yA
yA
Комплексный чертеж – это чертеж, состоящий из
двух и более ортогональных проекций геометрического образа.
Получается совмещением трех плоскостей проекций
в одну
Получается совмещением трех плоскостей проекций
в одну
0
АХ
АУ
АZ
АУ
Линии, перпендикулярные к осям
и соединяющие параллельные проекции, называются
линиями проекционной связи
П1
П2
П3
(от. фр. глагола еpurer – улучшать, исправлять рисунок)
