- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Наглядные изображения презентация
Содержание
- 1. Наглядные изображения
- 2. Лекция 6 Солодухин Е.А., 2017
- 3. Наглядные изображения
- 7. Аксонометрические проекции
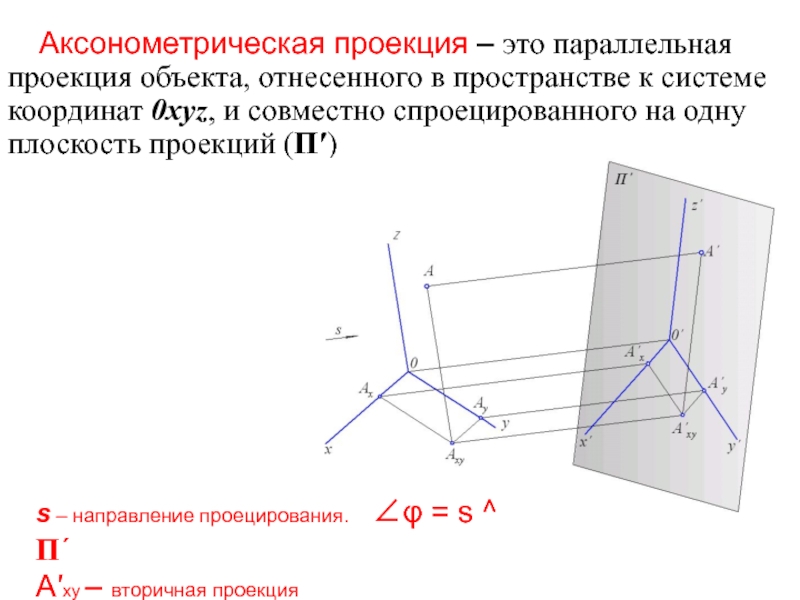
- 8. Аксонометрическая проекция – это параллельная проекция объекта,
- 9. Виды аксонометрических проекций в зависимости от направления
- 10. В прямоугольной аксонометрии ни одна из координатных
- 11. Коэффициенты искажения размеров по аксонометрическим осям
- 12. Виды аксонометрических проекций в зависимости от соотношения
- 13. Стандартные аксонометрические проекции ЕСКД ГОСТ 2.317-69*
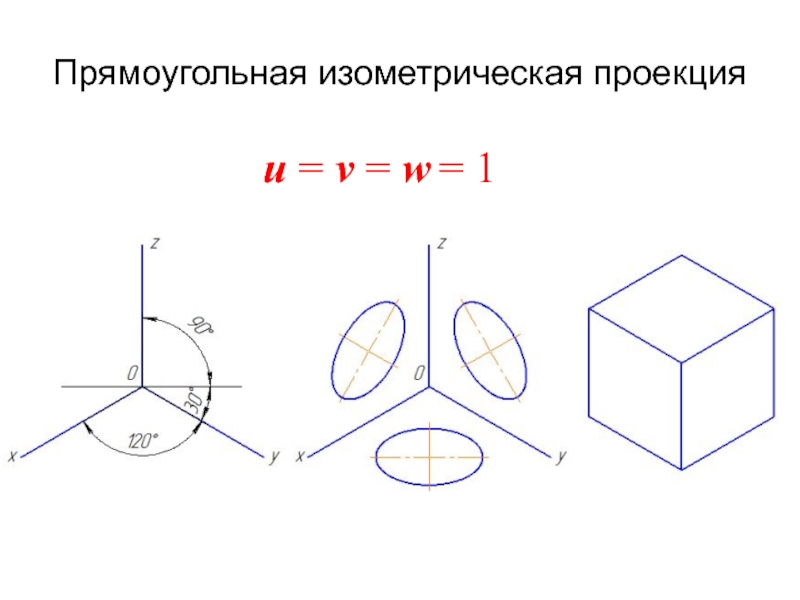
- 14. Прямоугольная изометрическая проекция u = v = w = 1
- 15. Косоугольная горизонтальная изометрическая проекция Плоскость x0y II
- 16. Линейная перспектива
- 17. Перспективой называют центральную проекцию объекта, на которую
- 18. Виды перспективы На плоскости – линейная перспектива.
- 19. Общий принцип построения перспективы точки SA ∩
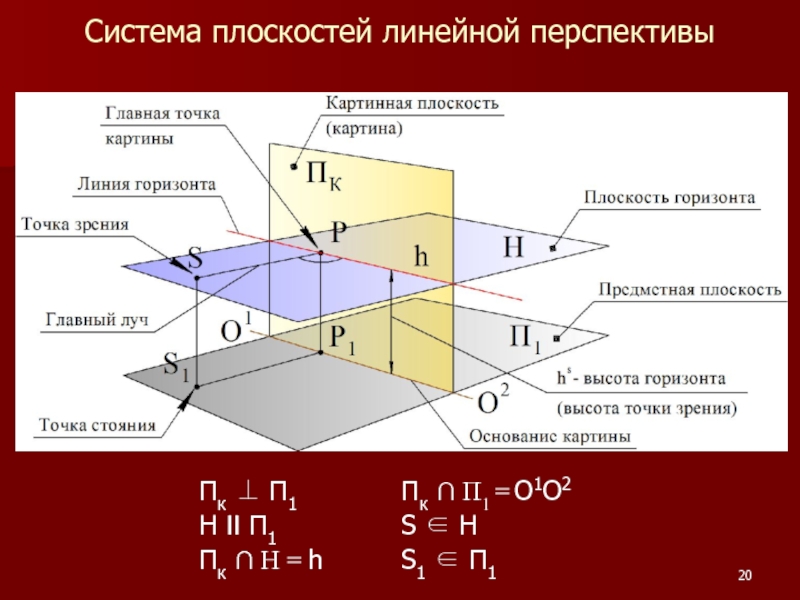
- 20. Система плоскостей линейной перспективы Пк ⊥ П1
- 21. Перспектива точек предметного пространства Если точка принадлежит
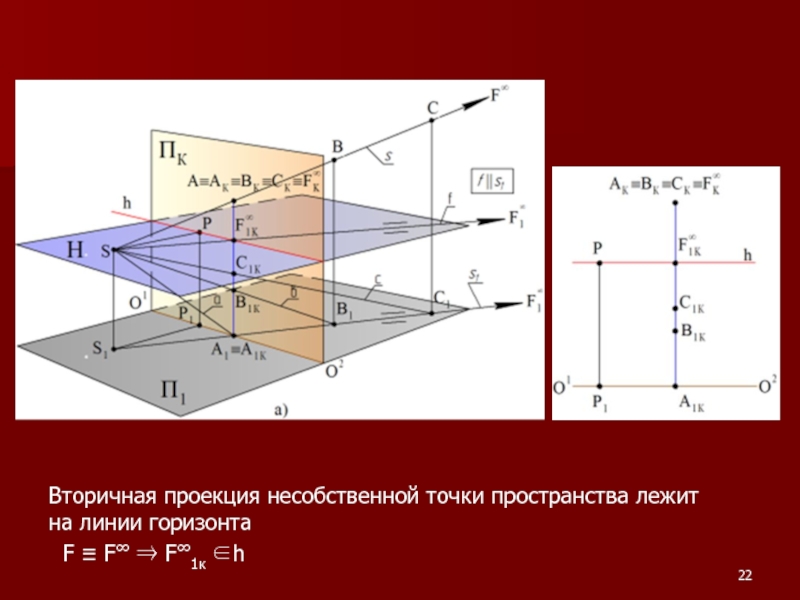
- 22. Вторичная проекция несобственной точки пространства лежит на
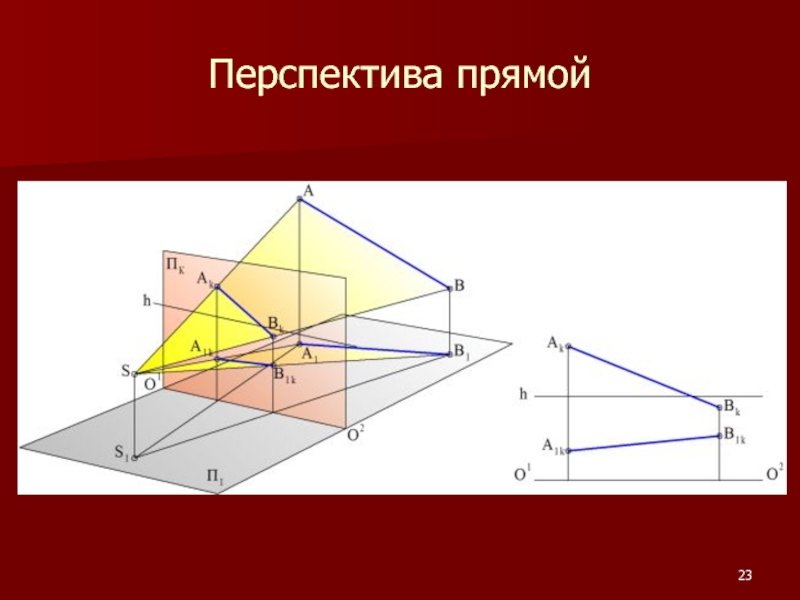
- 23. Перспектива прямой
- 24. В перспективе прямая (например, m) задается двумя
- 26. Чтобы получить (увидеть) несобственную точку F∞, принадлежащую
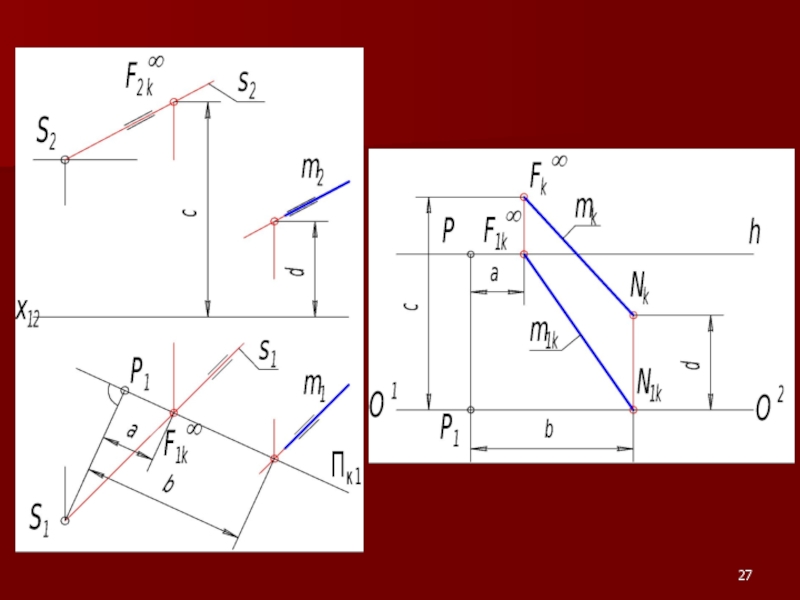
- 28. ∞ По положению точки F∞k относительно линии
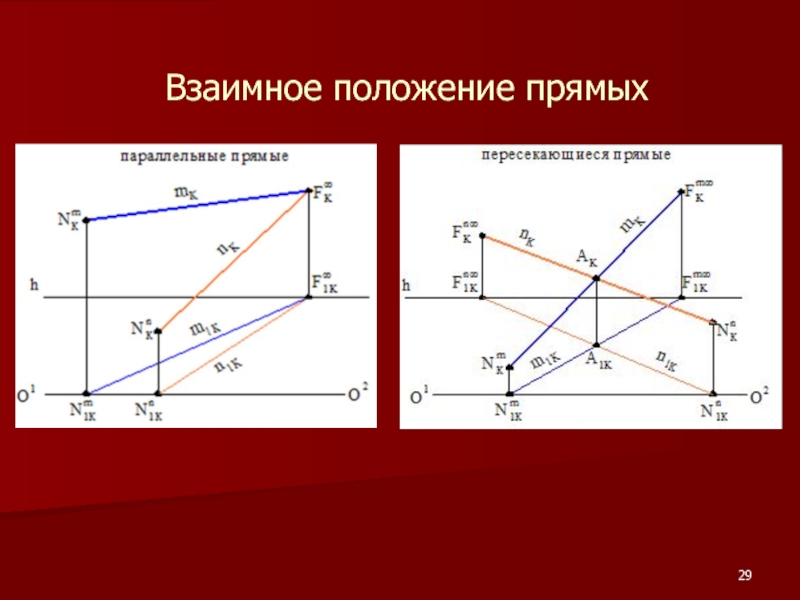
- 29. Взаимное положение прямых
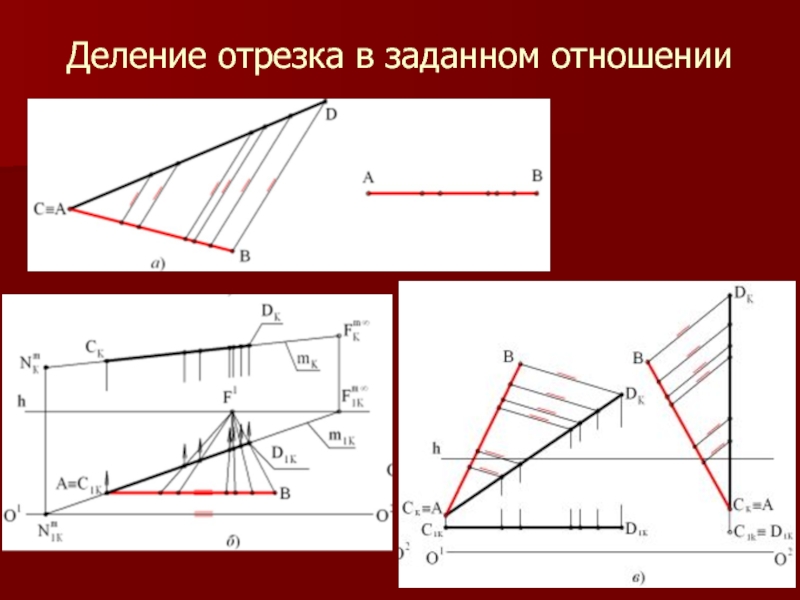
- 30. Деление отрезка в заданном отношении
Лекция 6 Солодухин Е.А., 2017
Слайд 1НАЧЕРТАТЕЛЬНАЯ ГЕОМЕТРИЯ
Направления обучения
«Архитектура»
«Реконструкция и реставрация архитектурного наследия»
«Дизайн архитектурной среды»
«Градостроительство»
Слайд 8Аксонометрическая проекция – это параллельная проекция объекта, отнесенного в пространстве к
системе координат 0xyz, и совместно спроецированного на одну плоскость проекций (П′)
s – направление проецирования. ∠φ = s ^ П´
А′xy – вторичная проекция
Слайд 9Виды аксонометрических проекций в зависимости от направления проецирования
Прямоугольные (s ⊥ П′
∧ ∠φ = 90º)
Косоугольные (s ⊥ П′ ∧ ∠φ ≠ 90º)
Косоугольные (s ⊥ П′ ∧ ∠φ ≠ 90º)
Слайд 10В прямоугольной аксонометрии ни одна из координатных плоскостей системы 0xyz не
может быть расположена параллельно плоскости проекций П´.
В косоугольной аксонометрии одна из координатных плоскостей системы 0xyz может быть расположена параллельно плоскости проекций П´.
В косоугольной аксонометрии одна из координатных плоскостей системы 0xyz может быть расположена параллельно плоскости проекций П´.
Расположение пространственной системы координат 0xyz относительно плоскости проекций
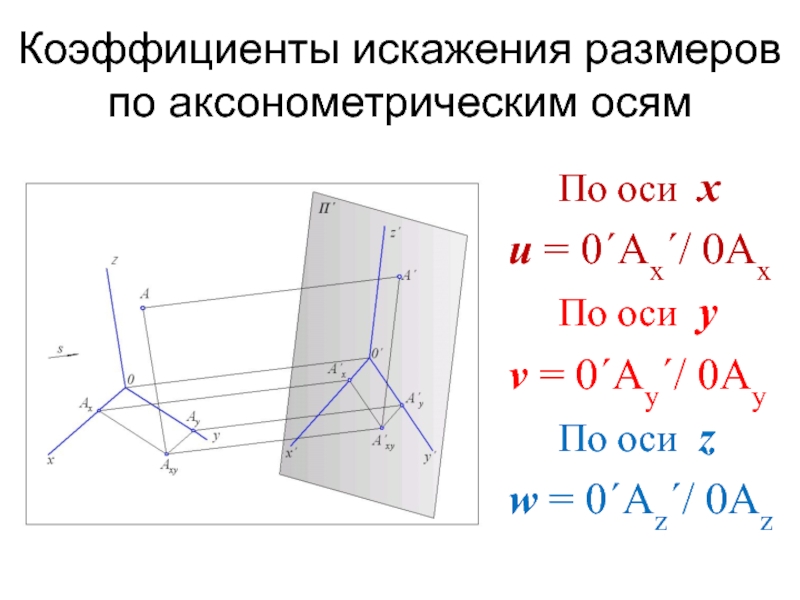
Слайд 11Коэффициенты искажения размеров по аксонометрическим осям
По оси x
u
= 0´Ax´/ 0Ax
По оси y
v = 0´Ay´/ 0Ay
По оси z
w = 0´Az´/ 0Az
По оси y
v = 0´Ay´/ 0Ay
По оси z
w = 0´Az´/ 0Az
Слайд 12Виды аксонометрических проекций в зависимости от соотношения величин коэффициентов искажения по
аксонометрическим осям
u = v = w - изометрия
u = v ≠ w
u ≠ v = w - диметрия
u ≠ w = v
u ≠ v ≠ w ≠ u - триметрия
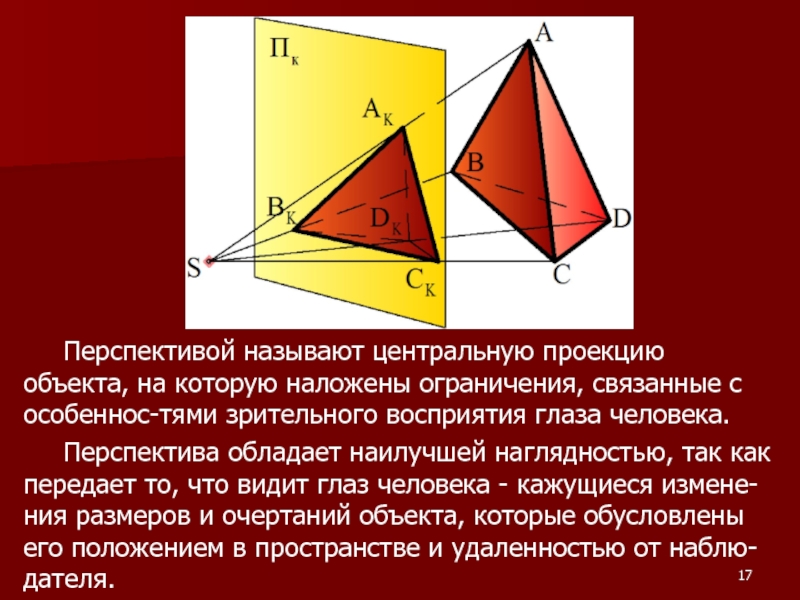
Слайд 17 Перспективой называют центральную проекцию объекта, на которую наложены ограничения, связанные с
особеннос-тями зрительного восприятия глаза человека.
Перспектива обладает наилучшей наглядностью, так как передает то, что видит глаз человека - кажущиеся измене-ния размеров и очертаний объекта, которые обусловлены его положением в пространстве и удаленностью от наблю-дателя.
Перспектива обладает наилучшей наглядностью, так как передает то, что видит глаз человека - кажущиеся измене-ния размеров и очертаний объекта, которые обусловлены его положением в пространстве и удаленностью от наблю-дателя.
Слайд 18Виды перспективы
На плоскости – линейная перспектива. Если плоскость расположена горизонтально, то
перспектива плафонная (для росписи потолков).
На цилиндрической поверхности – панорамная перспектива.
На сферической поверхности – купольная перспектива.
На цилиндрической поверхности – панорамная перспектива.
На сферической поверхности – купольная перспектива.
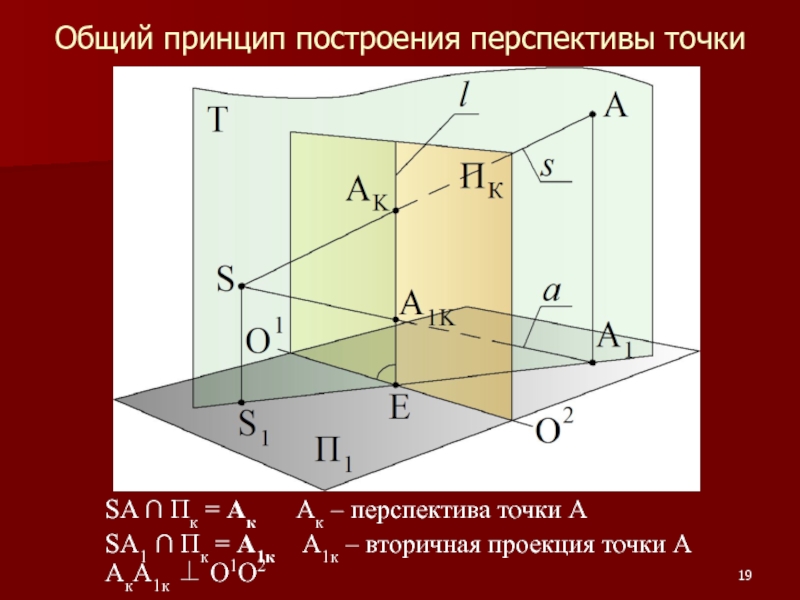
Слайд 19Общий принцип построения перспективы точки
SA ∩ Пк = Ак
Ак – перспектива точки А
SA1 ∩ Пк = А1к А1к – вторичная проекция точки А АкА1к ⊥ О1О2
SA1 ∩ Пк = А1к А1к – вторичная проекция точки А АкА1к ⊥ О1О2
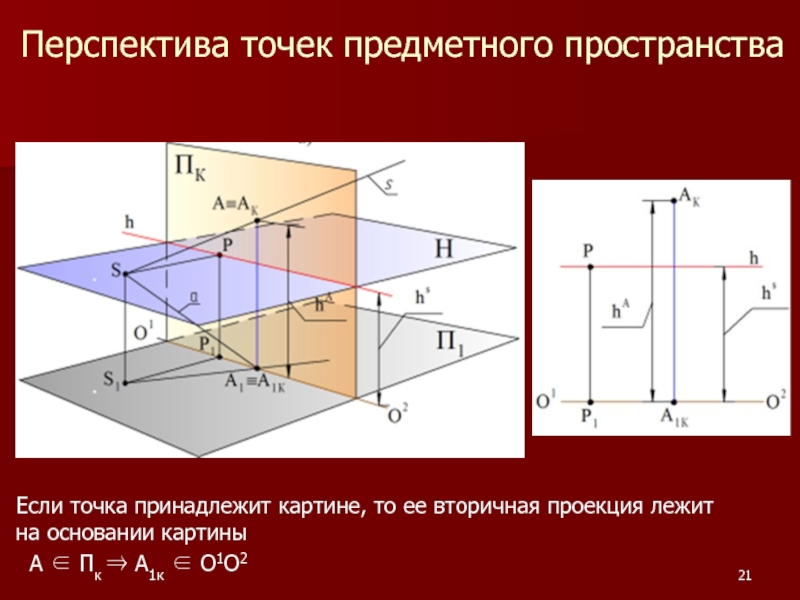
Слайд 21Перспектива точек предметного пространства
Если точка принадлежит картине, то ее вторичная проекция
лежит на основании картины
А ∈ Пк ⇒ А1к ∈ О1О2
А ∈ Пк ⇒ А1к ∈ О1О2
Слайд 22Вторичная проекция несобственной точки пространства лежит на линии горизонта
F ≡
F∞ ⇒ F∞1к ∈h
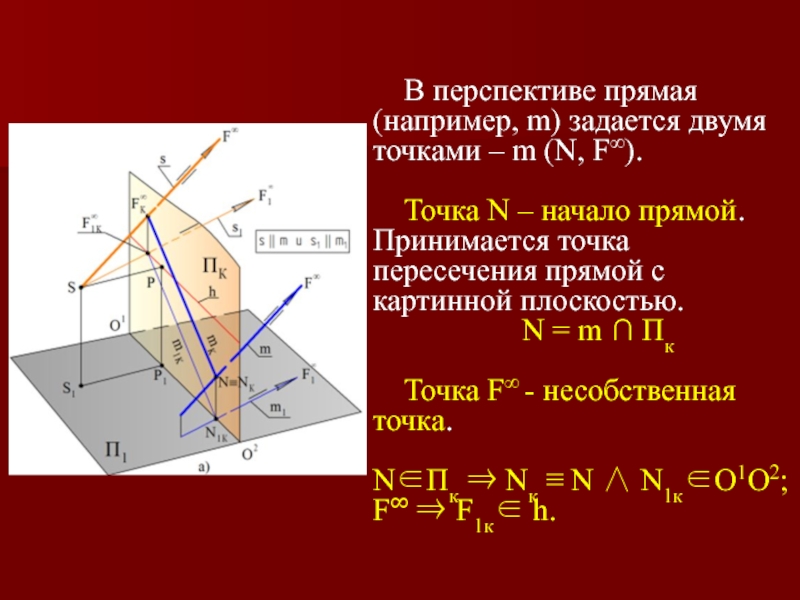
Слайд 24В перспективе прямая (например, m) задается двумя точками – m (N,
F∞).
Точка N – начало прямой. Принимается точка пересечения прямой с картинной плоскостью.
N = m ∩ Пк
Точка F∞ - несобственная точка.
N∈Пк ⇒ Nк ≡ N ∧ N1к∈O1O2; F∞ ⇒ F1к∈ h.
Точка N – начало прямой. Принимается точка пересечения прямой с картинной плоскостью.
N = m ∩ Пк
Точка F∞ - несобственная точка.
N∈Пк ⇒ Nк ≡ N ∧ N1к∈O1O2; F∞ ⇒ F1к∈ h.
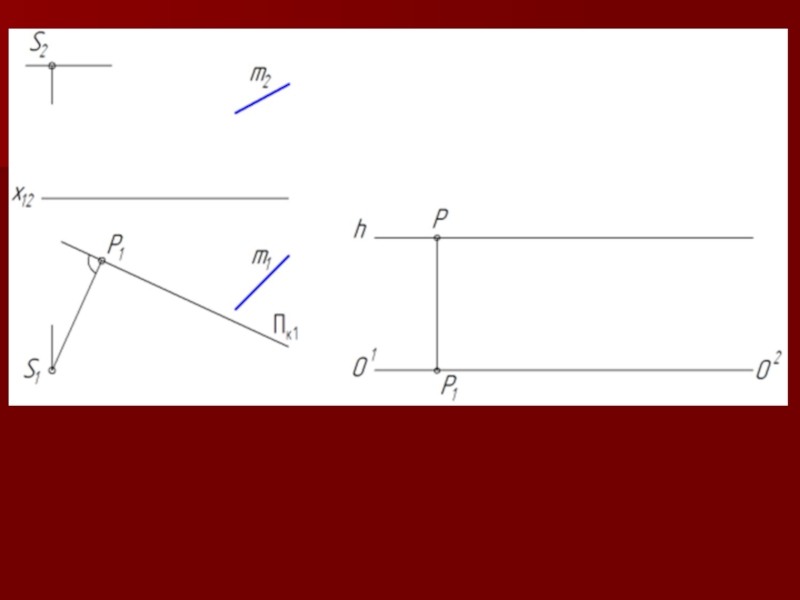
Слайд 26Чтобы получить (увидеть) несобственную точку F∞, принадлежащую прямой m, находясь в
точке зрения S, необходимо направить луч зрения параллельно прямой m.
Точка F∞k пересечения луча s с картинной плоскостью Пk и будет изображением несобственной точки F∞.
S∈s, s II m и s ∩ Пk = F∞k
Чтобы получить точку N начала прямой m, необходимо продолжить прямую до пересечения с картинной плоскостью
m ∩ Пк= N
Точка F∞k пересечения луча s с картинной плоскостью Пk и будет изображением несобственной точки F∞.
S∈s, s II m и s ∩ Пk = F∞k
Чтобы получить точку N начала прямой m, необходимо продолжить прямую до пересечения с картинной плоскостью
m ∩ Пк= N
Слайд 28∞
По положению точки F∞k относительно линии горизонта
можно судить о положении
прямой m относительно
предметной плоскости.
Если F∞k выше линии горизонта, то прямая восходящая.
Если F∞k ниже линии горизонта, то прямая нисходящая.
Если F∞k лежит на линии горизонта, т.е. F∞k ≡ F∞1k , то прямая
является горизонталью.
предметной плоскости.
Если F∞k выше линии горизонта, то прямая восходящая.
Если F∞k ниже линии горизонта, то прямая нисходящая.
Если F∞k лежит на линии горизонта, т.е. F∞k ≡ F∞1k , то прямая
является горизонталью.
