искажения
Плоскость. Способы задания плоскости. Плоскости частного положения (уровня и проецирующие)
Следы плоскости.
Принадлежность точки и прямой плоскости.
Главные линии плоскости.
Определение угла наклона плоскости к плоскостям проекций.
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Начертательная геометрия. Лекция 2 презентация
Содержание
- 1. Начертательная геометрия. Лекция 2
- 2. Следы прямой линии
- 3. Следы прямой линии Чтобы найти горизонтальный след
- 4. Взаимное положение прямых Прямые между собой могут быть: Параллельны Пересекаться скрещиваться
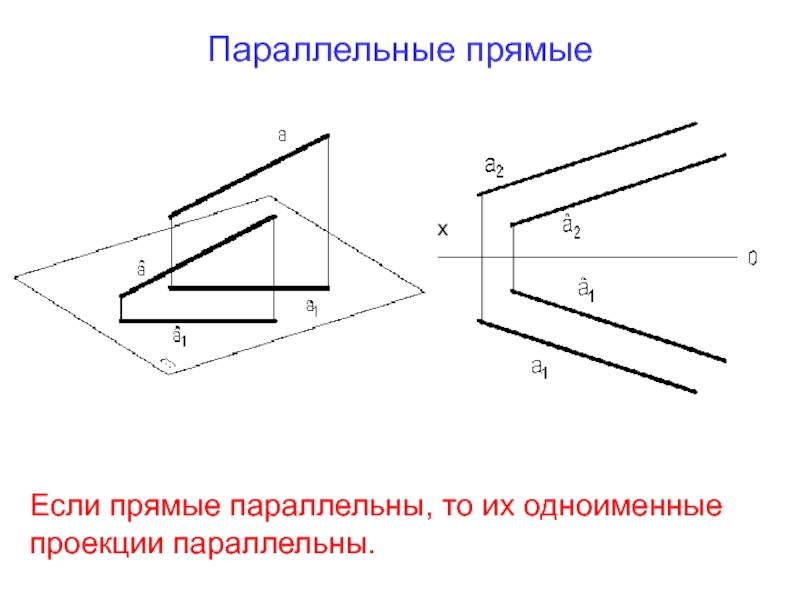
- 5. Параллельные прямые Если прямые параллельны, то их одноименные проекции параллельны. х
- 6. Пересекающиеся прямые Если прямые пересекаются, то
- 7. Скрещивающиеся прямые Если не выполняются условия параллельности или пересечения, прямые называются скрещивающимися
- 8. Скрещивающиеся прямые Например, в случае а) на
- 9. В пространстве расположим прямой угол АВС
- 10. Поднимем отрезок ВС за вершину С
- 11. Теорема о проецировании прямого угла h2
- 12. Геометрическая модель плоскости Плоскость задается движением
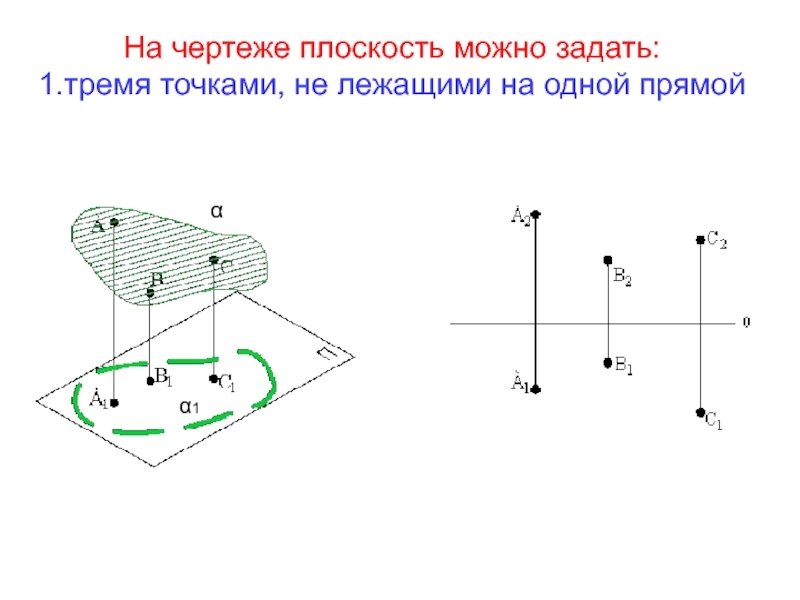
- 13. На чертеже плоскость можно задать: 1.тремя точками, не лежащими на одной прямой α α1
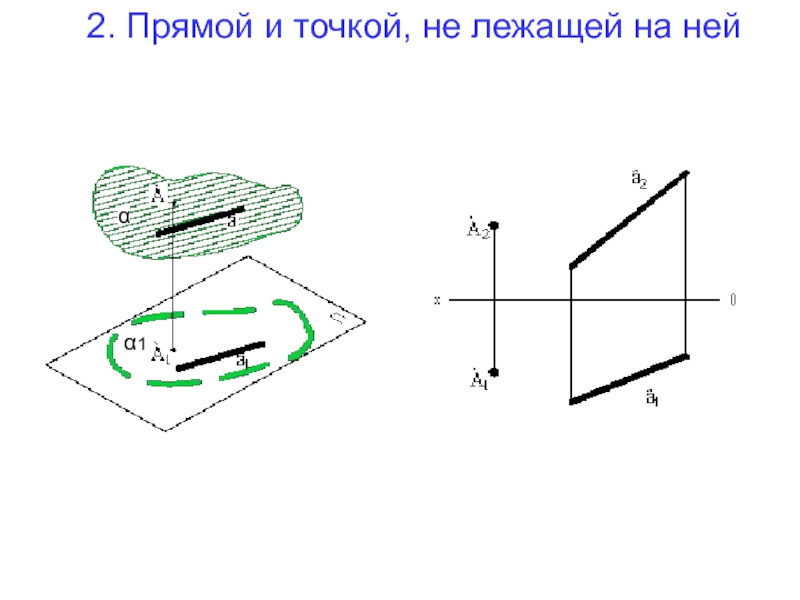
- 14. 2. Прямой и точкой, не лежащей на ней α α1
- 15. 3. Двумя параллельными прямыми α α1 α 2 α 1 b b1 b2 b1
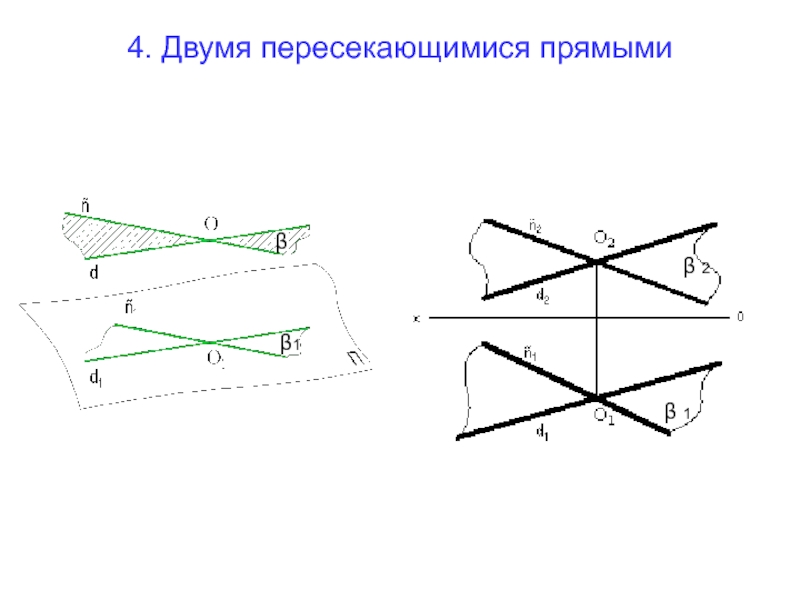
- 16. 4. Двумя пересекающимися прямыми β β1 β 2 β 1
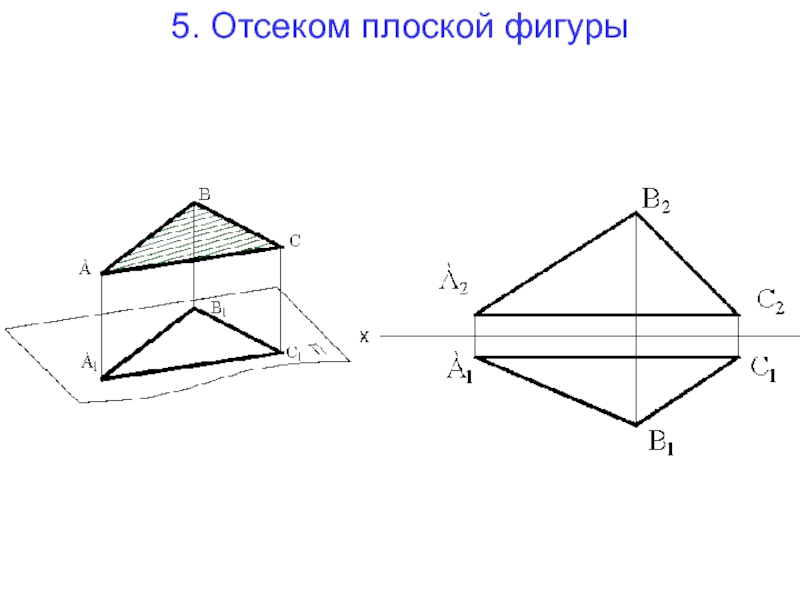
- 17. 5. Отсеком плоской фигуры
- 18. 6. Следами Следом плоскости называется линия пересечения
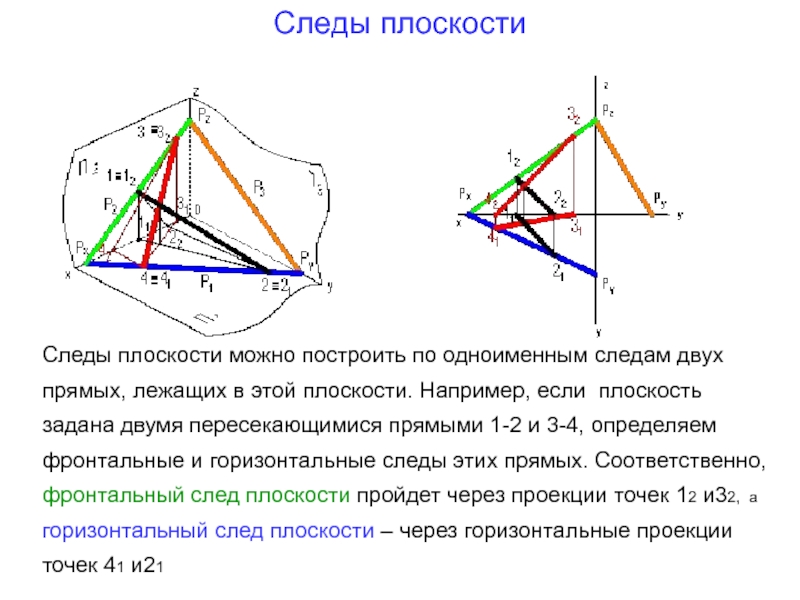
- 19. Следы плоскости Следы плоскости можно построить по
- 20. Плоскости уровня Горизонтальная плоскость уровня α α
- 21. Фронтальная плоскость уровня β β1 β3 β3
- 22. Профильная плоскость уровня Профильной плоскостью уровня называется
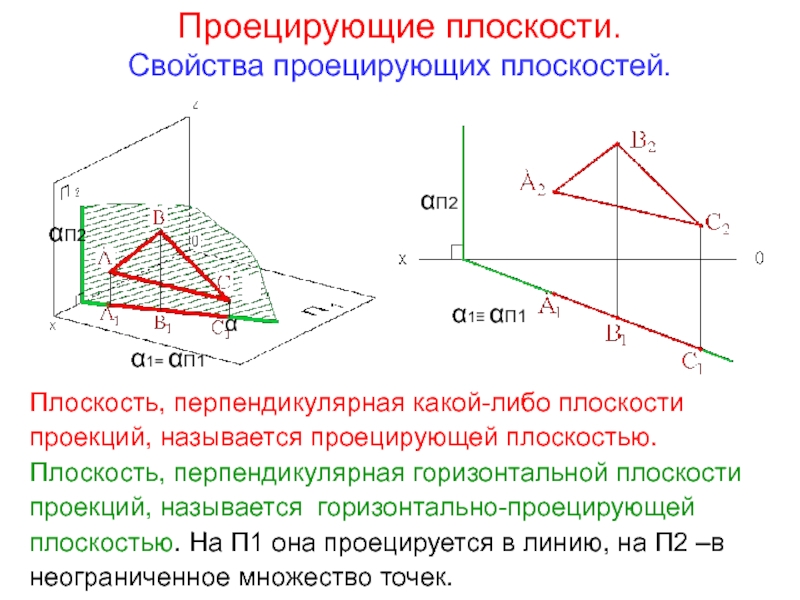
- 23. Проецирующие плоскости. Свойства проецирующих плоскостей. α αП2
- 24. Фронтально -проецирующая плоскость Фронтально-проецирующей называется плоскость, перпендикулярная
- 25. Профильно-проецирующая плоскость γ γП1 γ 3=γП3 γП2
- 26. Принадлежность прямой плоскости Прямая принадлежит плоскости, если
- 27. Принадлежность прямой плоскости Прямая принадлежит плоскости,
- 28. Принадлежность точки плоскости Точка принадлежит плоскости,
- 29. Главные линии плоскости: линии уровня и линии
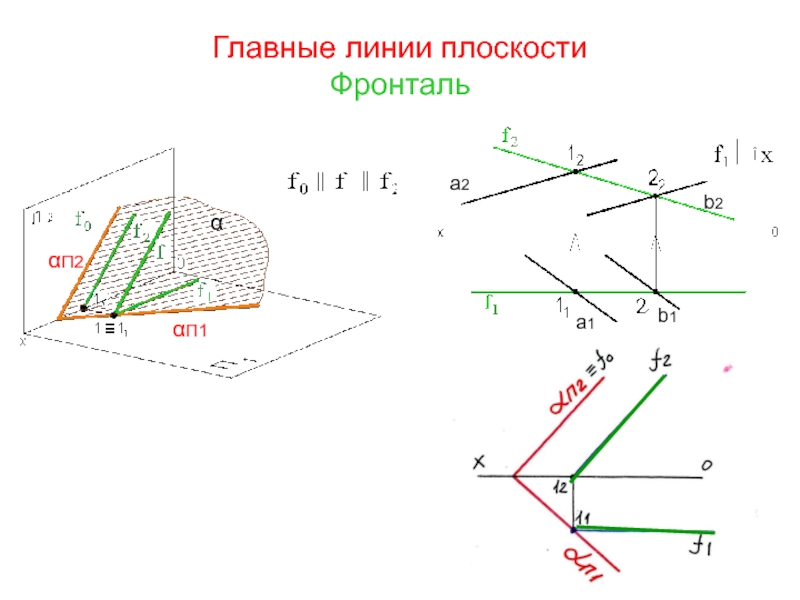
- 30. Главные линии плоскости Фронталь a2 b2 a1 b1 α αП2 αП1
- 31. Линия наибольшего наклона плоскости- прямая, лежащая
- 32. Определение угла наклона плоскости общего положения к
- 33. Задача: Определить угол наклона плоскости ΔАВС к
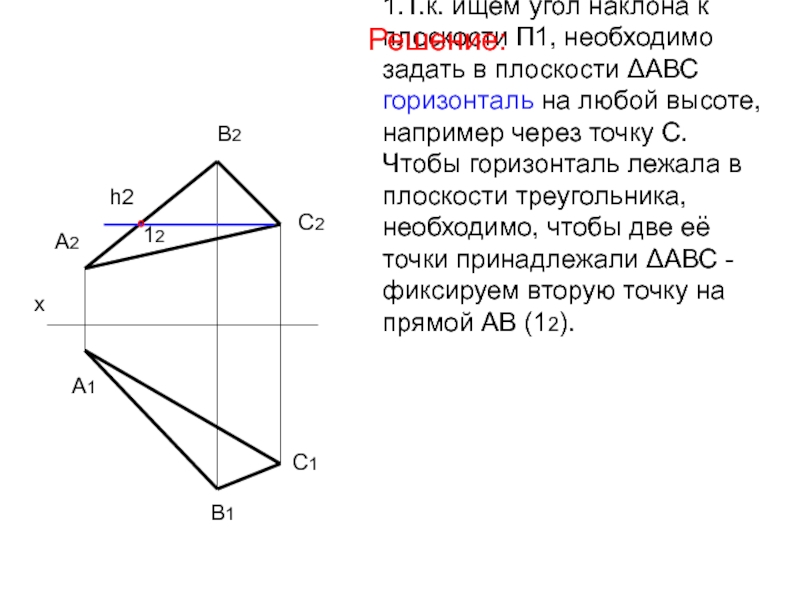
- 34. 1.Т.к. ищем угол наклона к плоскости П1,
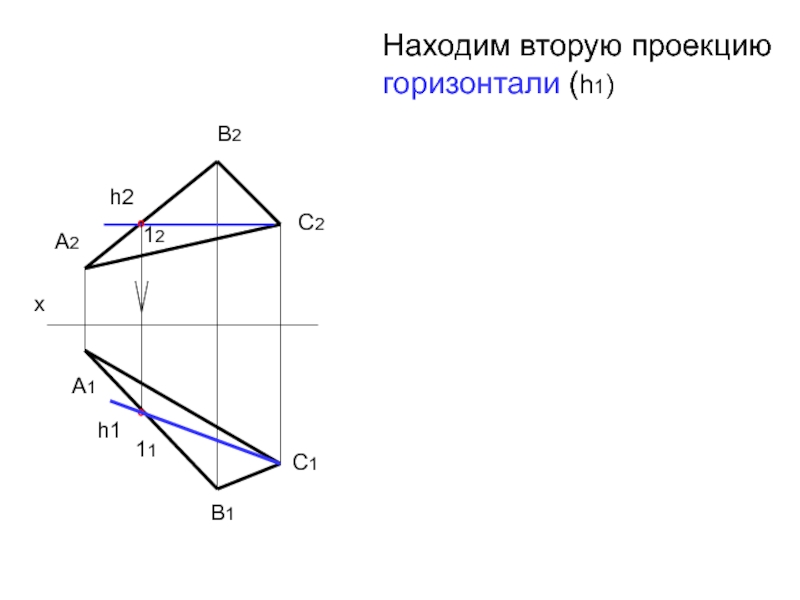
- 35. Находим вторую проекцию горизонтали (h1) х А2
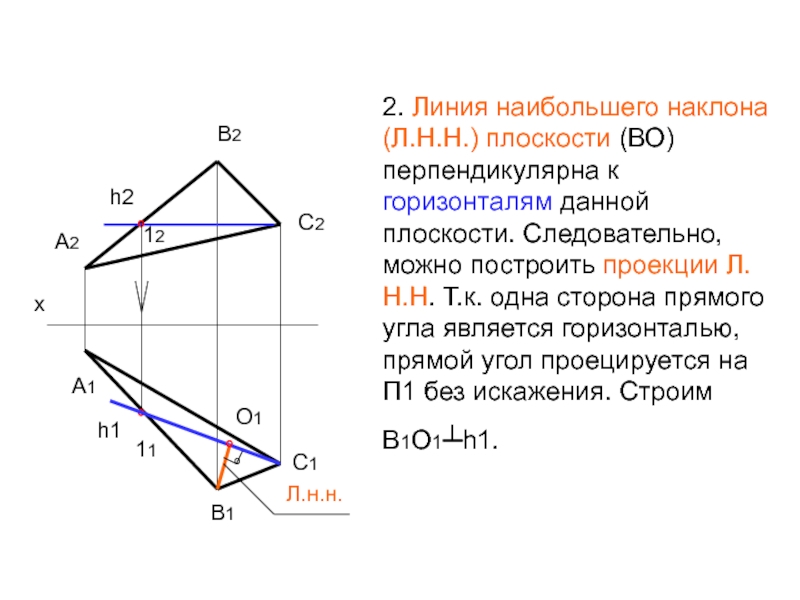
- 36. 2. Линия наибольшего наклона (Л.Н.Н.)
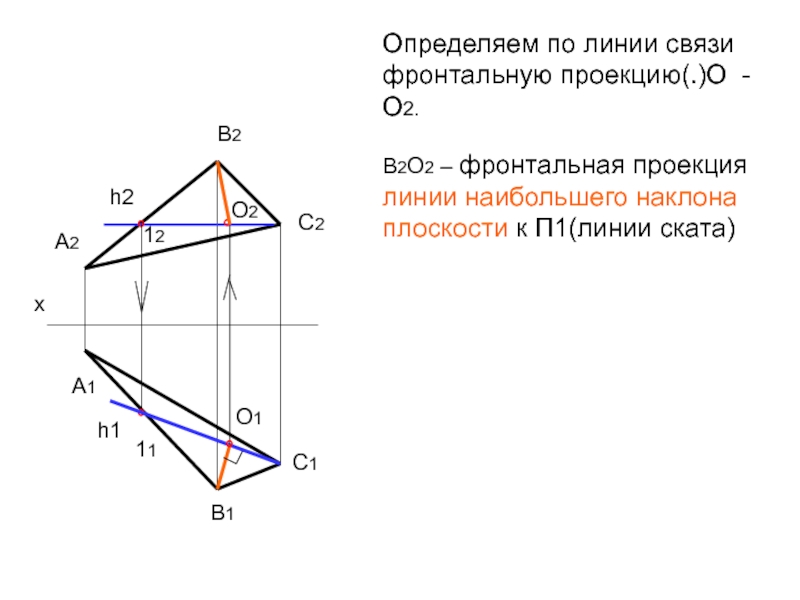
- 37. Определяем по линии связи фронтальную проекцию(.)О -
- 38. Угол наклона плоскости общего положения к плоскости
- 39. Натуральная величина отрезка ВО- гипотенуза треугольника.
Следы прямой линии Следом прямой называется точка пересечения прямой с плоскостью проекций. Н1 – горизонтальный след прямой; F2 – фронтальный след прямой.
Слайд 2
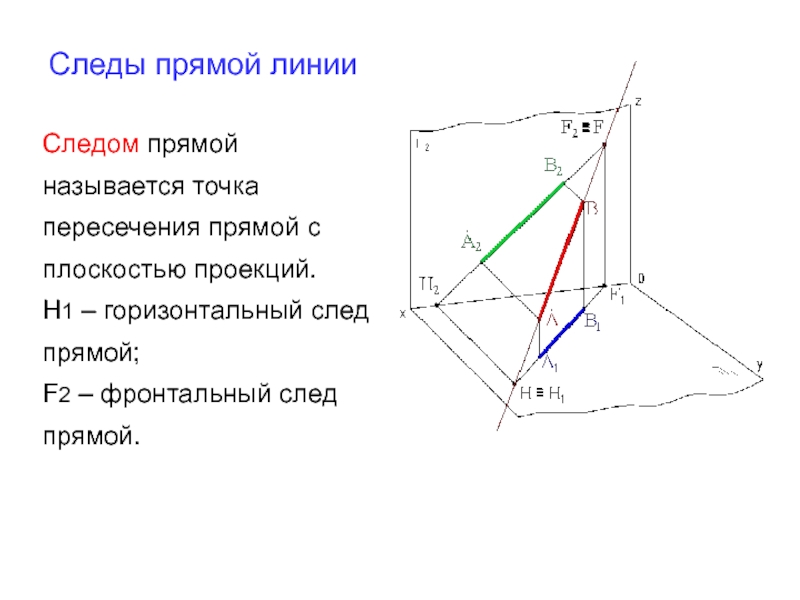
Следы прямой линии
Следом прямой
называется точка пересечения прямой с плоскостью проекций.
Н1
– горизонтальный след прямой;
F2 – фронтальный след прямой.
F2 – фронтальный след прямой.
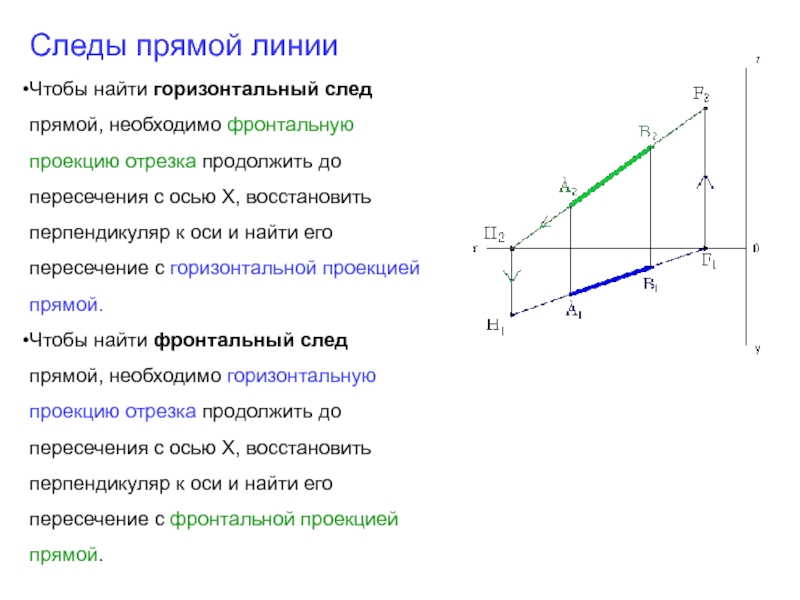
Слайд 3Следы прямой линии
Чтобы найти горизонтальный след прямой, необходимо фронтальную проекцию отрезка
продолжить до пересечения с осью Х, восстановить перпендикуляр к оси и найти его пересечение с горизонтальной проекцией прямой.
Чтобы найти фронтальный след прямой, необходимо горизонтальную проекцию отрезка продолжить до пересечения с осью Х, восстановить перпендикуляр к оси и найти его пересечение с фронтальной проекцией прямой.
Чтобы найти фронтальный след прямой, необходимо горизонтальную проекцию отрезка продолжить до пересечения с осью Х, восстановить перпендикуляр к оси и найти его пересечение с фронтальной проекцией прямой.
Слайд 6
Пересекающиеся прямые
Если прямые пересекаются, то на эпюре их одноименные проекции пересекаются
и проекции точки пересечения лежат на одной линии связи.
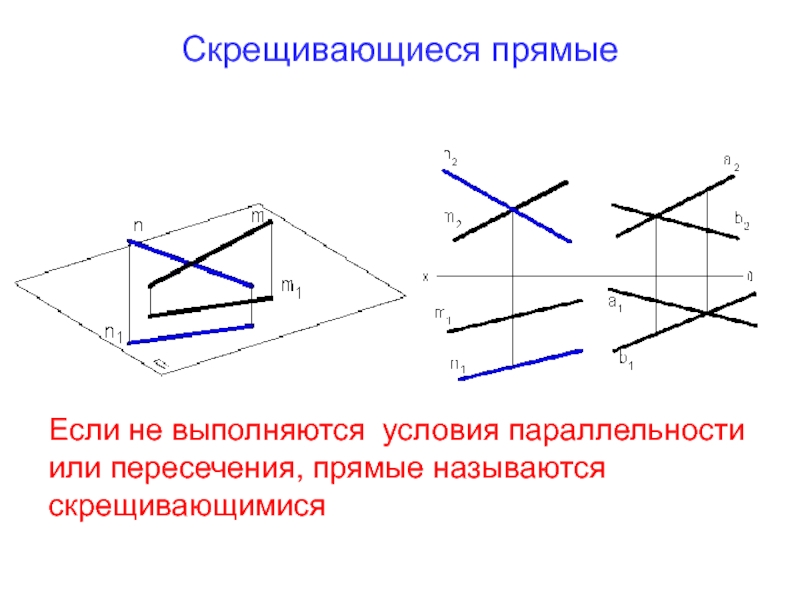
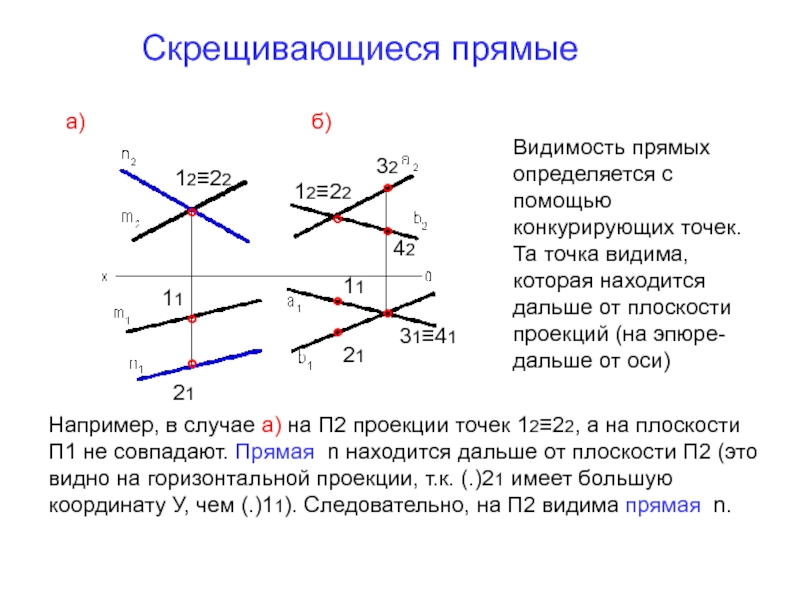
Слайд 7Скрещивающиеся прямые
Если не выполняются условия параллельности или пересечения, прямые называются скрещивающимися
Слайд 8Скрещивающиеся прямые
Например, в случае а) на П2 проекции точек 12≡22, а
на плоскости П1 не совпадают. Прямая n находится дальше от плоскости П2 (это видно на горизонтальной проекции, т.к. (.)21 имеет большую координату У, чем (.)11). Следовательно, на П2 видима прямая n.
12≡22
11
21
°
°
°
°
°
°
а)
б)
Видимость прямых определяется с помощью конкурирующих точек. Та точка видима, которая находится дальше от плоскости проекций (на эпюре- дальше от оси)
12≡22
11
21
°
°
32
31≡41
°
42
Слайд 9
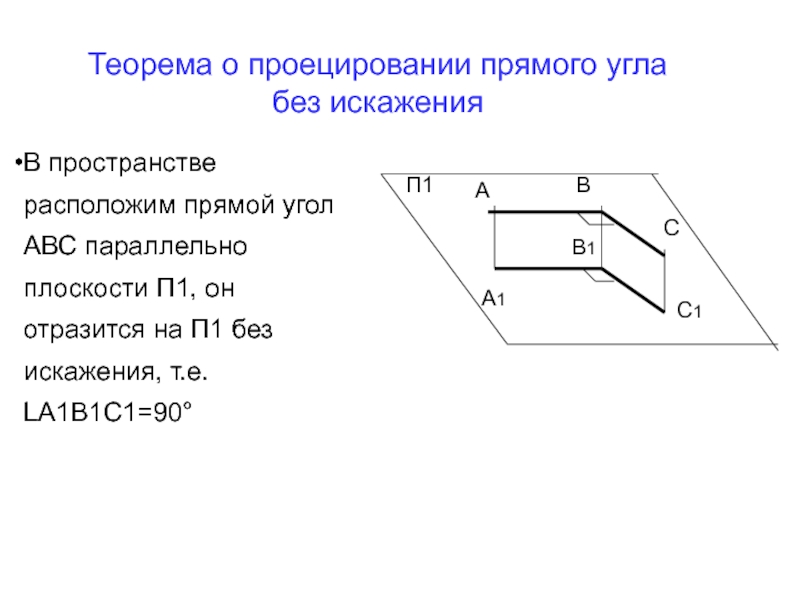
В пространстве расположим прямой угол АВС параллельно плоскости П1, он отразится
на П1 без искажения, т.е. LА1В1С1=90°
Теорема о проецировании прямого угла без искажения
А
В
С
А1
В1
С1
П1
Слайд 10
Поднимем отрезок ВС за вершину С . Проекция на П1 (В1С1)
сократится,
но А1В1 ┴ В1С1
Если одна сторона прямого угла параллельна плоскости, а вторая не перпендикулярна этой плоскости , прямой угол проецируется на данную плоскость без искажения
но А1В1 ┴ В1С1
Если одна сторона прямого угла параллельна плоскости, а вторая не перпендикулярна этой плоскости , прямой угол проецируется на данную плоскость без искажения
Теорема о проецировании прямого угла без искажения
А
В
С
А1
В1
С1
П1
С*
С1*
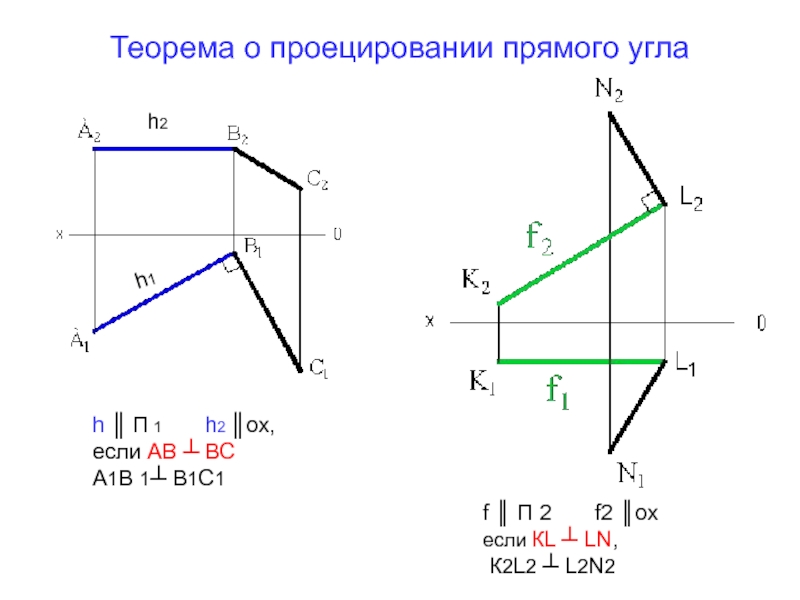
Слайд 11Теорема о проецировании прямого угла
h2
h1
h ║ П 1
h2 ║ох, если АВ ┴ ВС
А1В 1┴ В1С1
А1В 1┴ В1С1
f ║ П 2 f2 ║ох
если КL ┴ LN,
К2L2 ┴ L2N2
Слайд 12Геометрическая модель плоскости
Плоскость задается
движением прямой образующей линии « n »
по прямой направляющей линии «m» параллельно заданному направлению
« S »
« S »
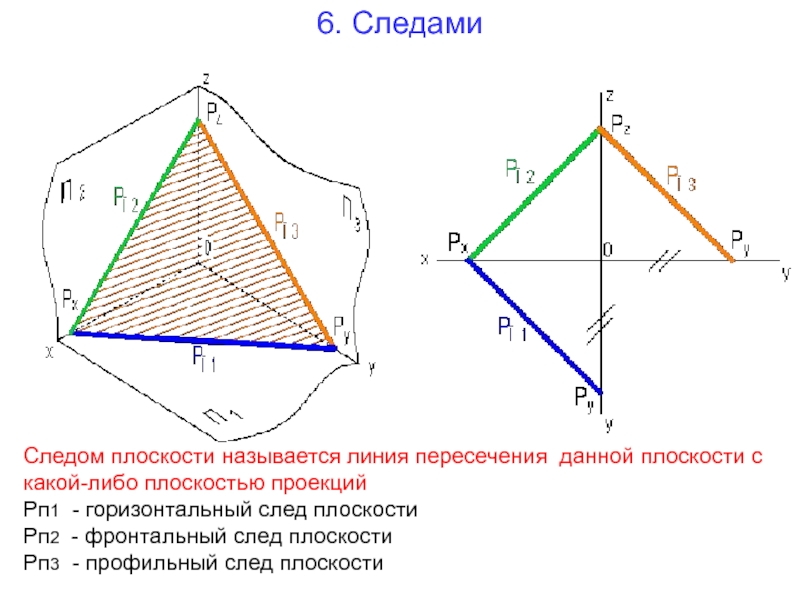
Слайд 186. Следами
Следом плоскости называется линия пересечения данной плоскости с какой-либо плоскостью
проекций
Рп1 - горизонтальный след плоскости
Рп2 - фронтальный след плоскости
Рп3 - профильный след плоскости
Рп1 - горизонтальный след плоскости
Рп2 - фронтальный след плоскости
Рп3 - профильный след плоскости
Слайд 19Следы плоскости
Следы плоскости можно построить по одноименным следам двух прямых, лежащих
в этой плоскости. Например, если плоскость задана двумя пересекающимися прямыми 1-2 и 3-4, определяем фронтальные и горизонтальные следы этих прямых. Соответственно, фронтальный след плоскости пройдет через проекции точек 12 и32, а горизонтальный след плоскости – через горизонтальные проекции точек 41 и21
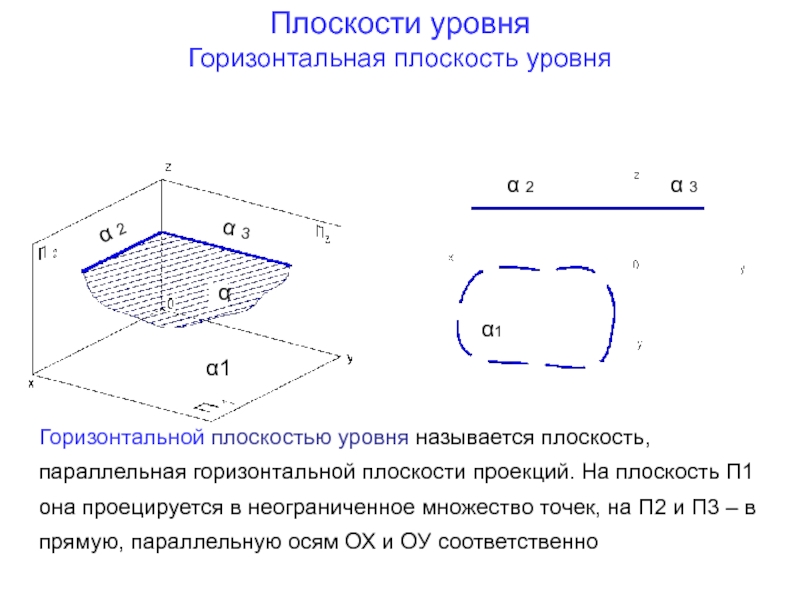
Слайд 20Плоскости уровня
Горизонтальная плоскость уровня
α
α 2
α 3
α 2
α 3
α1
Горизонтальной плоскостью уровня называется
плоскость, параллельная горизонтальной плоскости проекций. На плоскость П1 она проецируется в неограниченное множество точек, на П2 и П3 – в прямую, параллельную осям ОХ и ОУ соответственно
α1
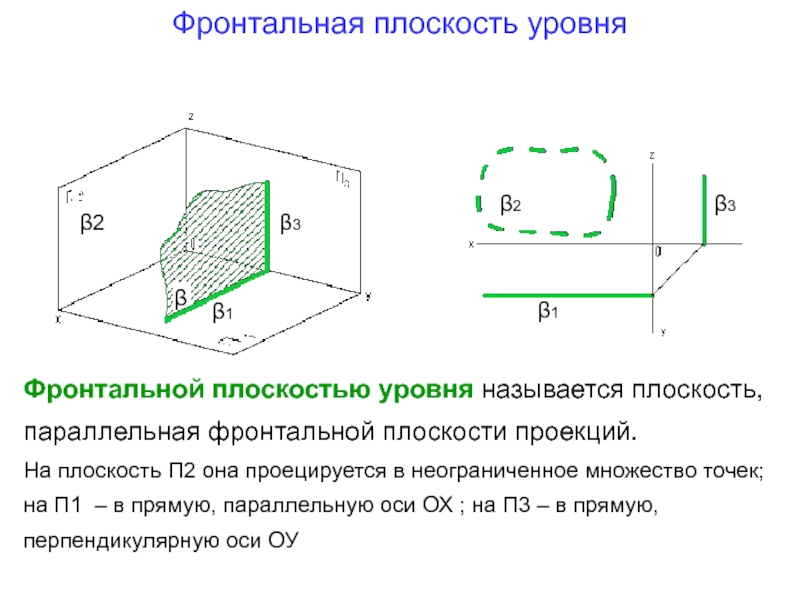
Слайд 21Фронтальная плоскость уровня
β
β1
β3
β3
β1
β2
Фронтальной плоскостью уровня называется плоскость, параллельная фронтальной плоскости проекций.
На плоскость П2 она проецируется в неограниченное множество точек; на П1 – в прямую, параллельную оси ОХ ; на П3 – в прямую, перпендикулярную оси ОУ
β2
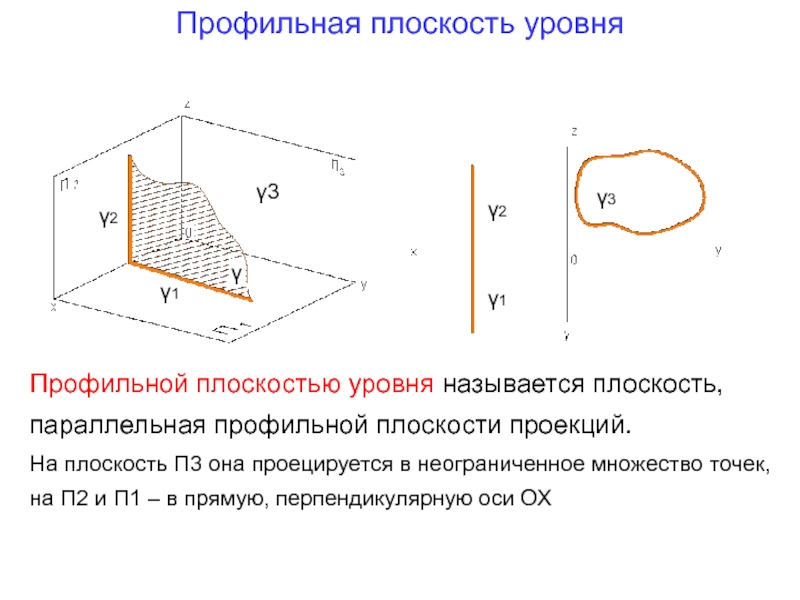
Слайд 22Профильная плоскость уровня
Профильной плоскостью уровня называется плоскость, параллельная профильной плоскости проекций.
На плоскость П3 она проецируется в неограниченное множество точек, на П2 и П1 – в прямую, перпендикулярную оси ОХ
γ
γ2
γ1
γ2
γ1
γ3
γ3
Слайд 23Проецирующие плоскости.
Свойства проецирующих плоскостей.
α
αП2
α1= αП1
αП2
α1≡ αП1
Плоскость, перпендикулярная какой-либо плоскости проекций, называется
проецирующей плоскостью.
Плоскость, перпендикулярная горизонтальной плоскости проекций, называется горизонтально-проецирующей плоскостью. На П1 она проецируется в линию, на П2 –в неограниченное множество точек.
Плоскость, перпендикулярная горизонтальной плоскости проекций, называется горизонтально-проецирующей плоскостью. На П1 она проецируется в линию, на П2 –в неограниченное множество точек.
Слайд 24Фронтально -проецирующая плоскость
Фронтально-проецирующей называется плоскость, перпендикулярная фронтальной плоскости проекций. На П2
она проецируется в линию, на П1 –в неограниченное множество точек. Фронтальный след этой плоскости совпадает с проекцией плоскости на П2 (β2 = βП2)
β
βП1
β2= βП2
β2 ≡βП2
βП1
β1
Слайд 25Профильно-проецирующая плоскость
γ
γП1
γ 3=γП3
γП2
γП2
γ П1
γ П3≡γ3
Профильно-проецирующей называется плоскость, перпендикулярная профильной плоскости
проекций. На П1 иП2 она проецируется в неограниченное множество точек. Проекция на П3 совпадает с профильным следом плоскости (γ П3=γ3).
γ1
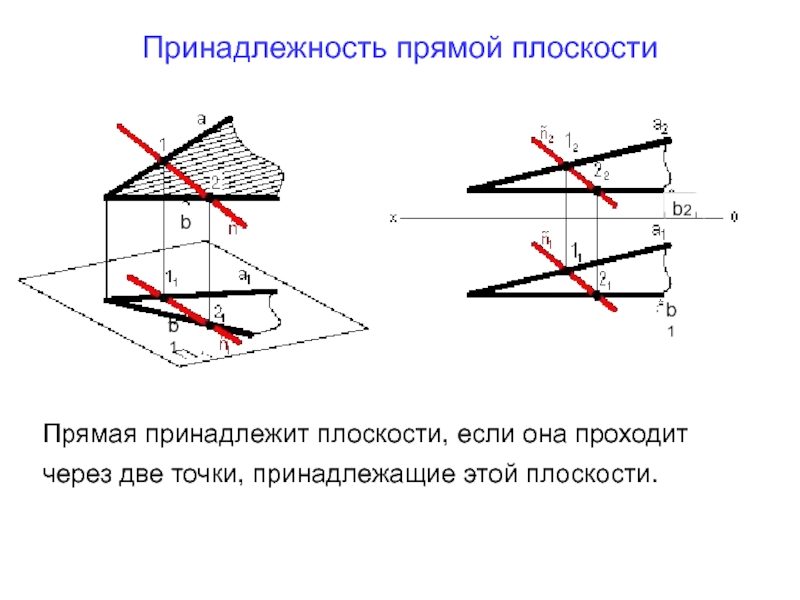
Слайд 26Принадлежность прямой плоскости
Прямая принадлежит плоскости, если она проходит через две точки,
принадлежащие этой плоскости.
b
b1
b1
b2
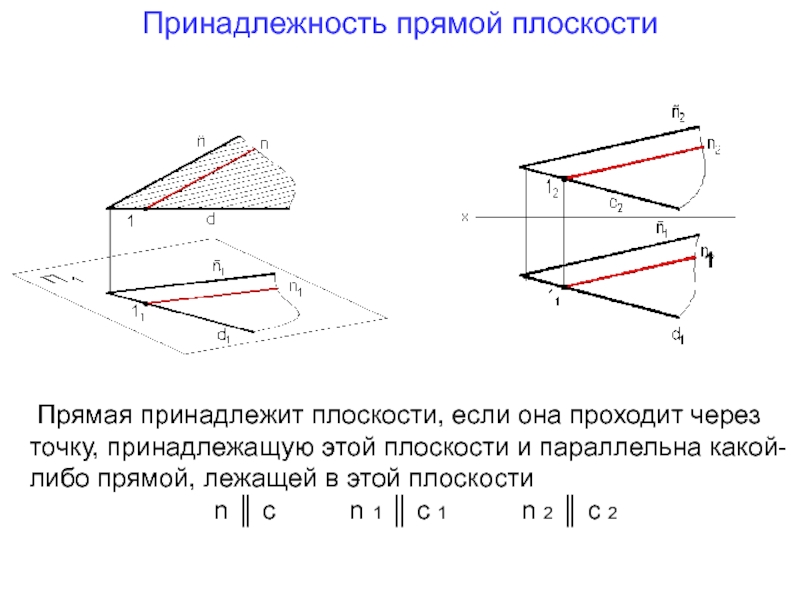
Слайд 27Принадлежность прямой плоскости
Прямая принадлежит плоскости, если она проходит через точку,
принадлежащую этой плоскости и параллельна какой-либо прямой, лежащей в этой плоскости
n ║ c n 1 ║ c 1 n 2 ║ c 2
n ║ c n 1 ║ c 1 n 2 ║ c 2
1
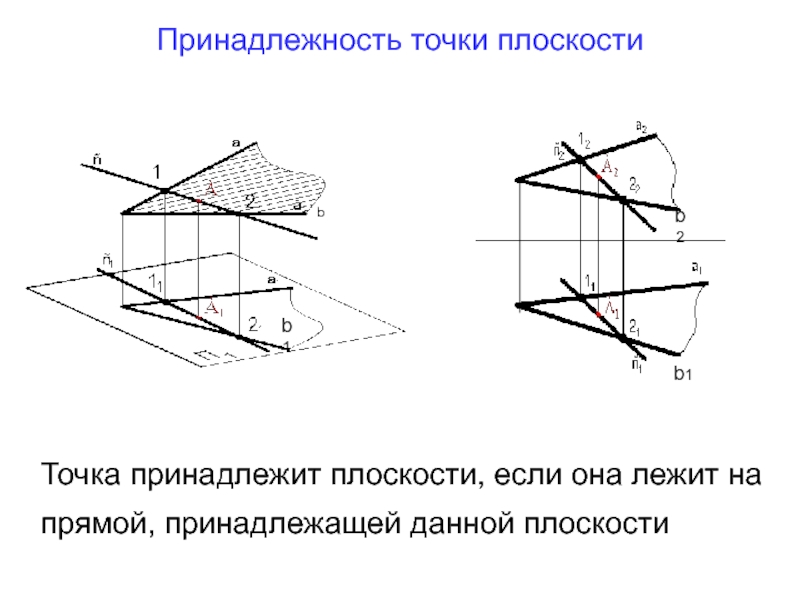
Слайд 28Принадлежность точки плоскости
Точка принадлежит плоскости, если она лежит на прямой,
принадлежащей данной плоскости
b1
b2
b1
b
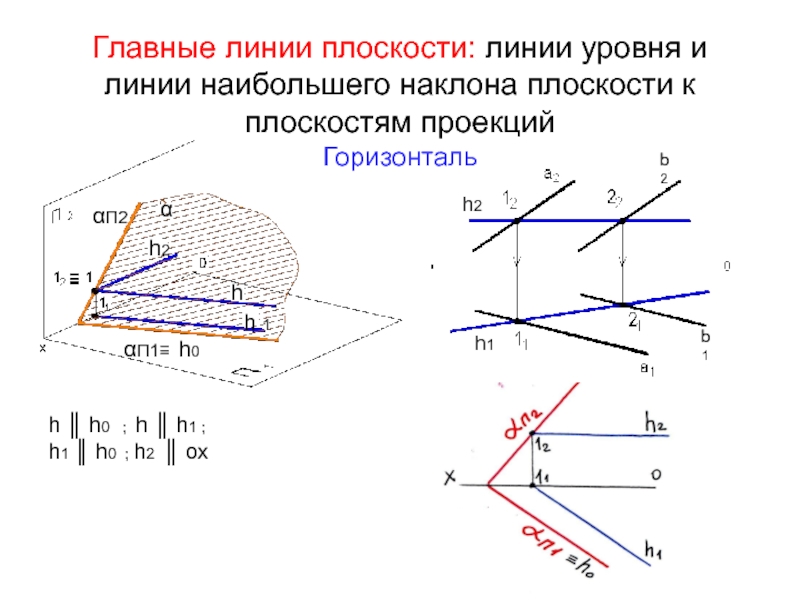
Слайд 29Главные линии плоскости: линии уровня и линии наибольшего наклона плоскости к
плоскостям проекций
Горизонталь
h
h 1
h2
α
h1
h2
h0
h ║ h0 ; h ║ h1 ; h1 ║ h0 ; h2 ║ ох
b2
b1
αП2
αП1≡
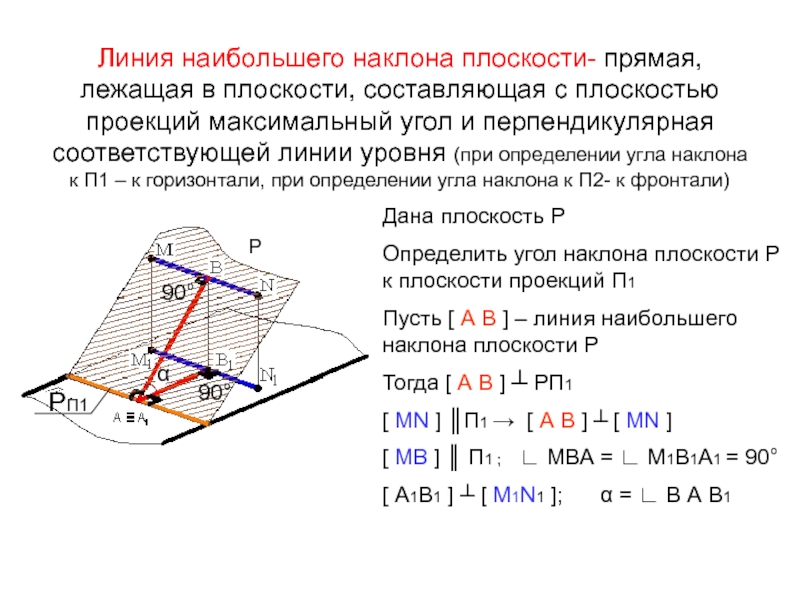
Слайд 31 Линия наибольшего наклона плоскости- прямая, лежащая в плоскости, составляющая с плоскостью
проекций максимальный угол и перпендикулярная соответствующей линии уровня (при определении угла наклона к П1 – к горизонтали, при определении угла наклона к П2- к фронтали)
Дана плоскость Р
Определить угол наклона плоскости Р к плоскости проекций П1
Пусть [ А В ] – линия наибольшего наклона плоскости Р
Тогда [ А В ] ┴ РП1
[ MN ] ║П1 → [ А В ] ┴ [ MN ]
[ МВ ] ║ П1 ; ∟ МВА = ∟ М1В1А1 = 90°
[ А1В1 ] ┴ [ M1N1 ]; α = ∟ В А В1
Р
РП1
α
90°
90°
Слайд 32Определение угла наклона плоскости общего положения к плоскости проекций
Угол наклона плоскости
общего положения к какой-либо плоскости проекций равен углу между натуральной величиной линии наибольшего наклона плоскости и ее проекцией на заданную плоскость проекций.
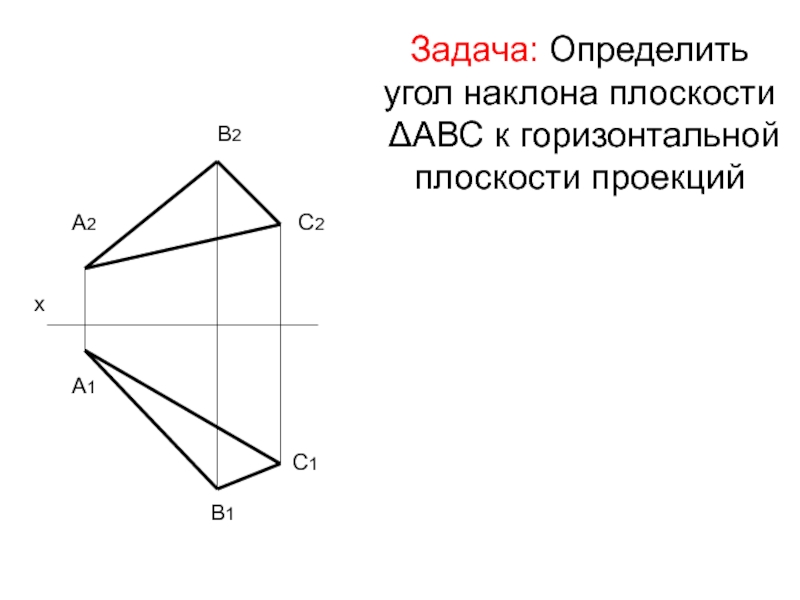
Слайд 33Задача: Определить угол наклона плоскости ΔАВС к горизонтальной плоскости проекций
х
А2
В2
С2
А1
В1
С1
Слайд 341.Т.к. ищем угол наклона к плоскости П1, необходимо задать в плоскости
ΔАВС горизонталь на любой высоте, например через точку С.
Чтобы горизонталь лежала в плоскости треугольника, необходимо, чтобы две её точки принадлежали ΔАВС - фиксируем вторую точку на прямой АВ (12).
х
А2
В2
С2
А1
В1
С1
h2
Решение:
12
°
Слайд 36 2. Линия наибольшего наклона (Л.Н.Н.) плоскости (ВО) перпендикулярна к горизонталям данной
плоскости. Следовательно, можно построить проекции Л.Н.Н. Т.к. одна сторона прямого угла является горизонталью, прямой угол проецируется на П1 без искажения. Строим В1О1┴h1.
х
А2
В2
С2
А1
В1
С1
h2
12
°
°
11
h1
О1
°
°
Л.н.н.
Слайд 37Определяем по линии связи фронтальную проекцию(.)О - О2. В2О2 – фронтальная проекция
линии наибольшего наклона плоскости к П1(линии ската)
х
А2
В2
С2
А1
В1
С1
h2
12
°
°
11
h1
О1
О2
°
°
Слайд 38Угол наклона плоскости общего положения к плоскости П1 равен углу между
линией наибольшего наклона и её горизонтальной проекцией.
Следовательно необходимо найти натуральную величину ВО, сделав построения на плоскости П1.
Построим прямоугольный треугольник, у которого один катет – проекция ВО на П1(В1О1), а второй катет равен разности высот точек В и О (Δz)
х
А2
В2
С2
А1
В1
С1
h2
12
°
°
11
h1
О1
О2
°
°
Δz
Слайд 39Натуральная величина отрезка ВО- гипотенуза треугольника. Угол наклона плоскости ΔАВС к
плоскости П1- угол α (величину которого можно измерить с помощью транспортира)
х
А2
В2
С2
А1
В1
С1
h2
12
°
°
11
h1
О1
О2
°
°
Δz
Δz
Н.в.[ВО]
α
