- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Многоранники. Поверхности презентация
Содержание
- 1. Многоранники. Поверхности
- 2. Многораннники Многогранники – замкнутые пространственные фигуры, ограниченные
- 3. Призма Многогранник, две грани которого n-угольники
- 4. Пирамида Многогранник, у которого одна из
- 5. Усеченная пирамида Если пирамиду отсечь плоскостью параллельной основанию, то получим усеченную пирамиду. Основание
- 6. Правильные многогранники Многогранник называется правильным, если его
- 7. Общее положение многоранника Под изображением многогранников
- 8. Пересечение многогранника плоскостью Геометрическая фигура,
- 9. Построение сечений многогранников Сечение проецирующими плоскостями Основание
- 10. Построение сечений многогранников сечение плоскостью общего положения
- 11. Thank You
Слайд 2Многораннники
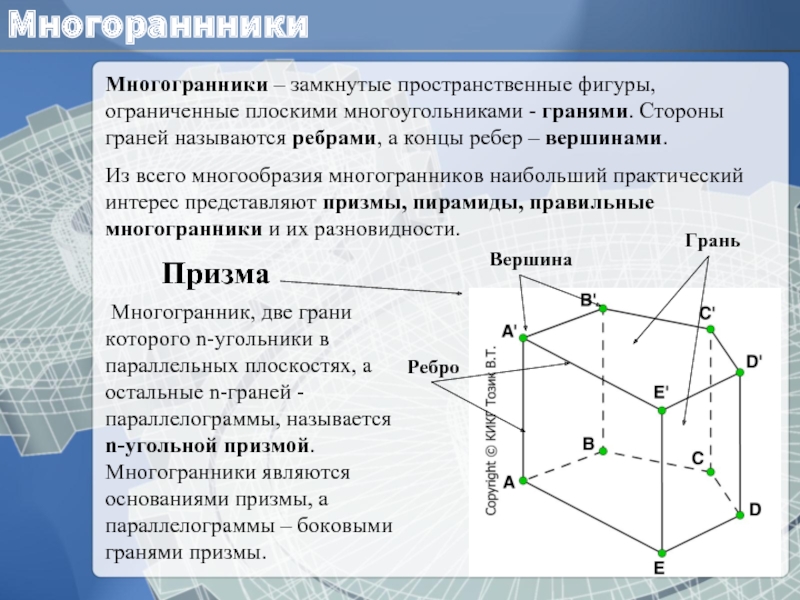
Многогранники – замкнутые пространственные фигуры, ограниченные плоскими многоугольниками - гранями. Стороны
Из всего многообразия многогранников наибольший практический интерес представляют призмы, пирамиды, правильные многогранники и их разновидности.
Многогранник, две грани которого n-угольники в параллельных плоскостях, а остальные n-граней - параллелограммы, называется n-угольной призмой. Многогранники являются основаниями призмы, а параллелограммы – боковыми гранями призмы.
Призма
Грань
Вершина
Ребро
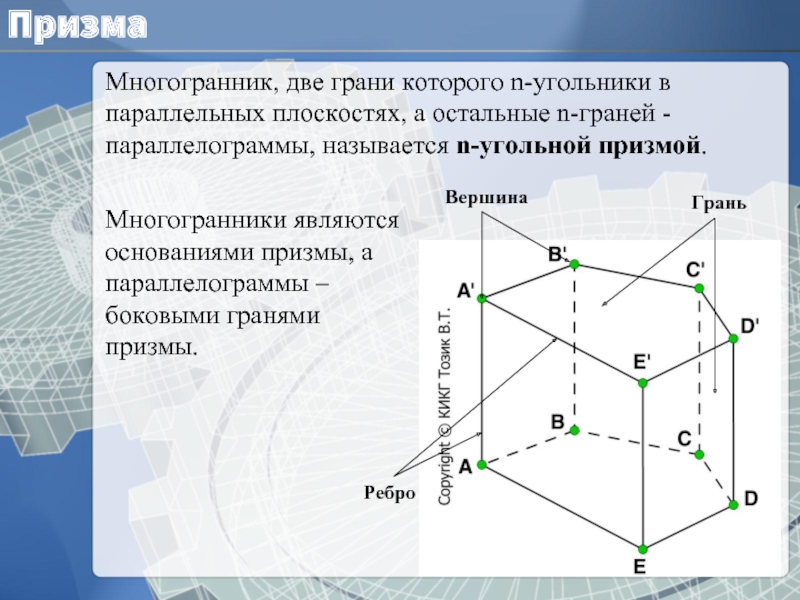
Слайд 3Призма
Многогранник, две грани которого n-угольники в параллельных плоскостях, а остальные
Основание
Многогранники являются основаниями призмы, а параллелограммы – боковыми гранями призмы.
Грань
Вершина
Ребро
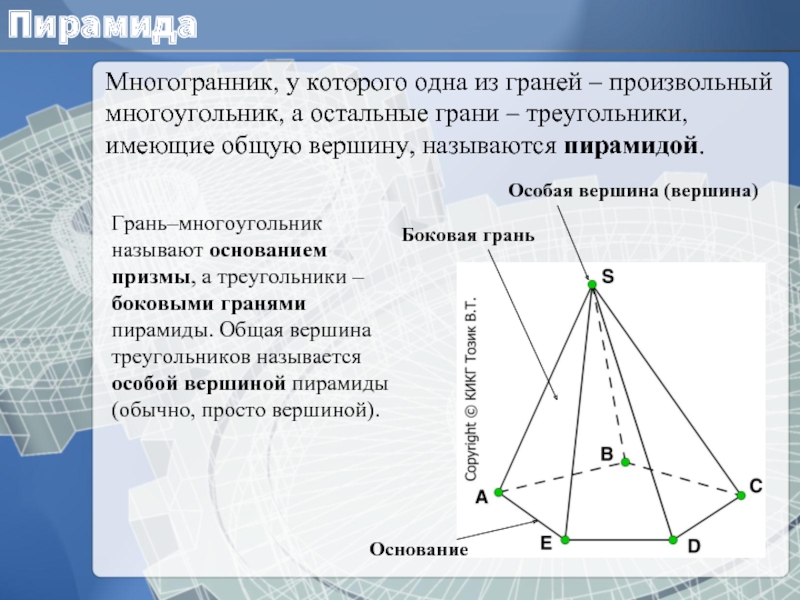
Слайд 4Пирамида
Многогранник, у которого одна из граней – произвольный многоугольник, а
Грань–многоугольник называют основанием призмы, а треугольники – боковыми гранями пирамиды. Общая вершина треугольников называется особой вершиной пирамиды (обычно, просто вершиной).
Особая вершина (вершина)
Основание
Основание
Боковая грань
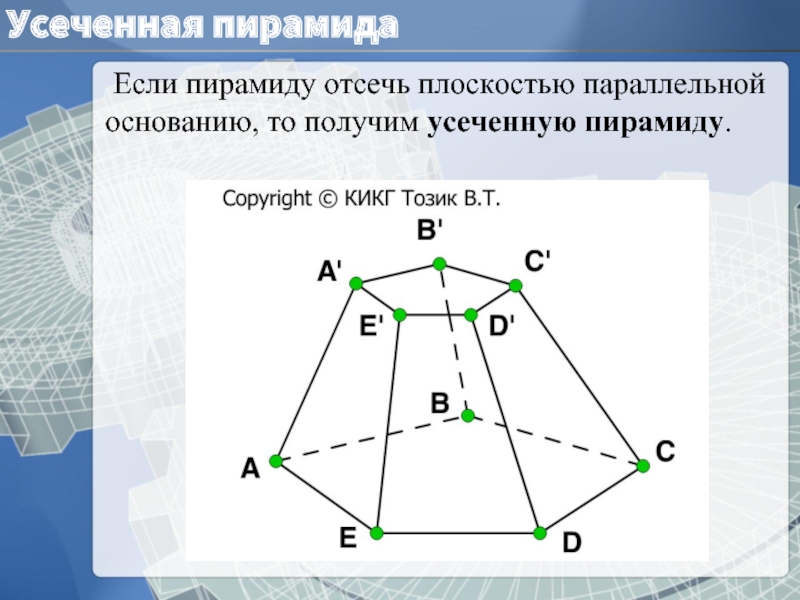
Слайд 5Усеченная пирамида
Если пирамиду отсечь плоскостью параллельной основанию, то получим усеченную
Основание
Слайд 6Правильные многогранники
Многогранник называется правильным, если его грани правильные многоугольники (т.е. такие,
Существует пять видов правильных многогранников:
куб, тетраэдр, октаэдр, додекаэдр, икосаэдр.
Основание
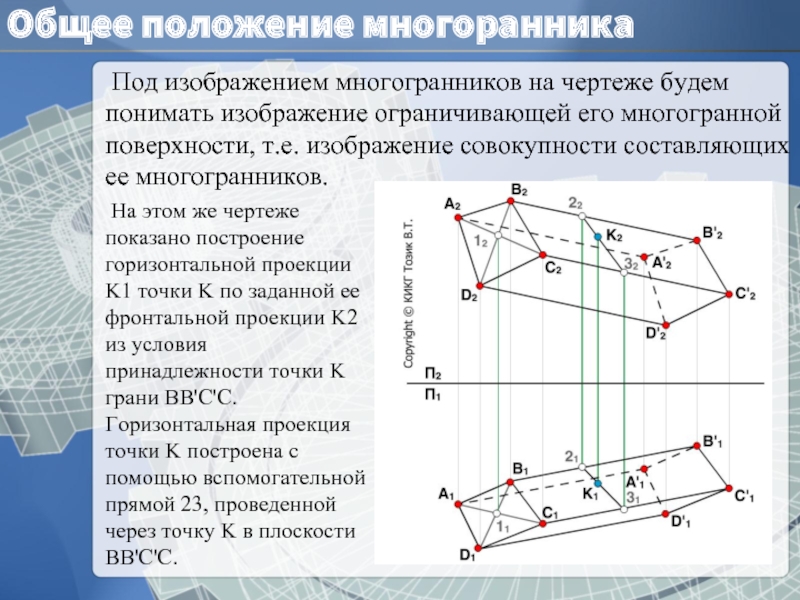
Слайд 7Общее положение многоранника
Под изображением многогранников на чертеже будем понимать изображение
Основание
На этом же чертеже показано построение горизонтальной проекции K1 точки K по заданной ее фронтальной проекции K2 из условия принадлежности точки K грани BB'C'C. Горизонтальная проекция точки K построена с помощью вспомогательной прямой 23, проведенной через точку K в плоскости BB'C'C.
Слайд 8 Пересечение многогранника плоскостью
Геометрическая фигура, получающаяся в результате пересечения многогранника
Сечение представляет собой плоский многоугольник с внутренней областью. В частном случае эти многоугольники могут распадаться на несколько многогранников, вырождаться в прямые и точки.
Сечение многогранника плоскостью можно построить двумя способами:
1. По точкам пересечения с плоскостью ребер многогранника.
2. По линиям пересечения граней многогранника с плоскостью.
В первом случае задача сводится к определению точек пересечения прямой с плоскостью. Во втором случае - к определению линий пересечения плоскостей.
В ряде случаев целесообразно комбинированное применение обоих способов.
Основание
Слайд 9Построение сечений многогранников
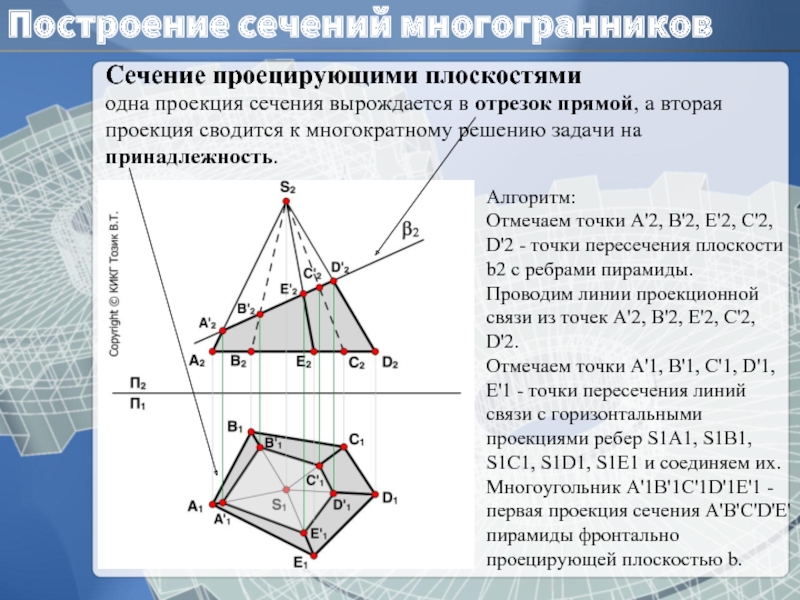
Сечение проецирующими плоскостями
Основание
одна проекция сечения вырождается в отрезок прямой,
Алгоритм:
Отмечаем точки А'2, B'2, E'2, C'2, D'2 - точки пересечения плоскости b2 с ребрами пирамиды.
Проводим линии проекционной связи из точек А'2, B'2, E'2, C'2, D'2.
Отмечаем точки А'1, B'1, C'1, D'1, E'1 - точки пересечения линий связи с горизонтальными проекциями ребер S1A1, S1B1, S1C1, S1D1, S1E1 и соединяем их.
Многоугольник А'1B'1C'1D'1E'1 - первая проекция сечения А'B'C'D'E' пирамиды фронтально проецирующей плоскостью b.
Слайд 10Построение сечений многогранников
сечение плоскостью общего положения
Основание
Грани и ребра призмы перпендикулярны
Алгоритм:
Отмечаем точки 11 и 21: 11 = А1В1∩ Е1D1, 21 = А1В1∩Е1F1.
Проводим линии проекционной связи через точки 11 и 21 и находим точки 12 и 22: 12 ∈Е2D2, 22 ∈Е2F2.
Проводим прямую 1222 до пересечения с проекциями ребер пирамиды в точках М2 и L2.
Отмечаем точки 31 и 41: 31 = А1С1 ∩ Е1D1, 41 = А1С1 ∩ D1F1.
По линиям связи находим точки 32 и 42: 32 ∈Е2D2, 42 ∈D2F2.
Проводим прямую 3242 до пересечения с проекцией ребра в точке N2.
Соединяем точки L2, M2 и N2.