Полное название гипара – гиперболический параболоид (или «косая плоскость»).
Поверхность гипара относится к линейчатым поверхностям, образующими и направляющими которых служат прямые линии.
Поверхность гипара образуется движением прямой образующей l по двум скрещивающимся прямолинейным направляющим a и b параллельно некоторой заданной плоскости параллелизма π
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Конструирование составной поверхности гипаров презентация
Содержание
- 1. Конструирование составной поверхности гипаров
- 2. Дано: Схема образования гиперболического параболоида ABCD и
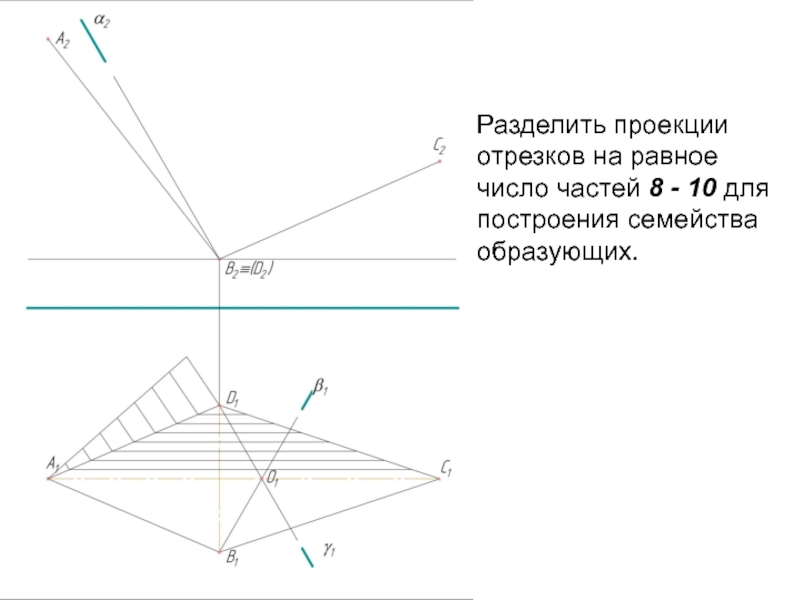
- 3. Разделить проекции отрезков на равное число частей 8 - 10 для построения семейства образующих.
- 4. Разделить проекции отрезков на равное число частей 8 - 10 для построения семейства образующих.
- 5. Разделить проекции отрезков на равное число частей 8 - 10 для построения семейства образующих.
- 6. Разделить проекции отрезков на равное число частей 8 - 10 для построения семейства образующих.
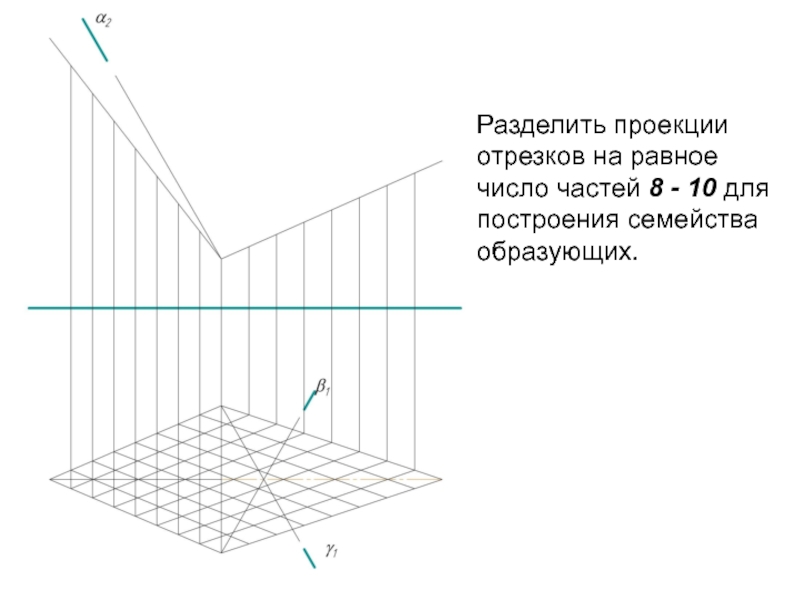
- 7. Построить два семейства образующих каркаса-сетки и очерк поверхности.
- 8. Построить проекции линий пересечения поверхности гипара с
- 9. Построить проекции линий пересечения поверхности гипара с
- 10. Построить проекции линий пересечения поверхности гипара с
- 11. Точка пересечения плоскостей α, γ и β
- 12. План и фасад комбинированной поверхности гипаров выполняется
- 13. Последовательно формируем границы отсеков с учетом их
- 14. Построить вид слева (дополнительный вид) комбинированной поверхности гипаров.
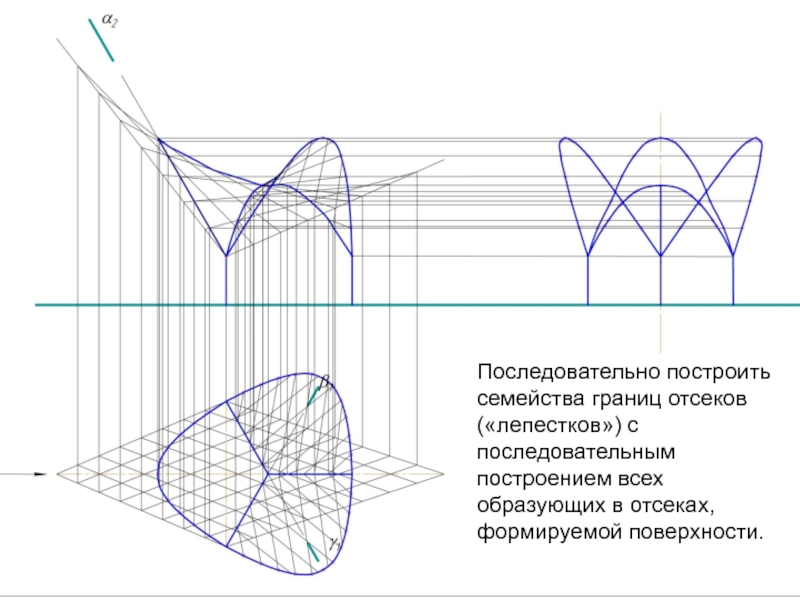
- 15. Последовательно построить семейства границ отсеков («лепестков») с последовательным построением всех образующих в отсеках, формируемой поверхности.
- 16. Оформляем работу в соответствии с ГОСТ.
Дано: Схема образования гиперболического параболоида ABCD и его отсеков. Двумя направляющими и двумя граничными образующими (или направляющими второго семейства) гипара являются пары скрещивающихся отрезков AB, CD и AD, BC. Исходный отсек
Слайд 1Задание 2.2. Конструирование
составной поверхности
гипаров.
Слайд 2Дано:
Схема образования гиперболического параболоида ABCD и его отсеков.
Двумя направляющими и двумя
граничными образующими (или направляющими второго семейства) гипара являются пары скрещивающихся отрезков AB, CD и AD, BC.
Исходный отсек гипара ограничен плоскостями: горизонтально-проецирующими γ и β (границы смежных отсеков) и фронтально-проецирующей плоскостью α (элемент границы искомой составной поверхности).
Исходный отсек гипара ограничен плоскостями: горизонтально-проецирующими γ и β (границы смежных отсеков) и фронтально-проецирующей плоскостью α (элемент границы искомой составной поверхности).
Слайд 3Разделить проекции отрезков на равное число частей 8 - 10 для
построения семейства образующих.
Слайд 4Разделить проекции отрезков на равное число частей 8 - 10 для
построения семейства образующих.
Слайд 5Разделить проекции отрезков на равное число частей 8 - 10 для
построения семейства образующих.
Слайд 6Разделить проекции отрезков на равное число частей 8 - 10 для
построения семейства образующих.
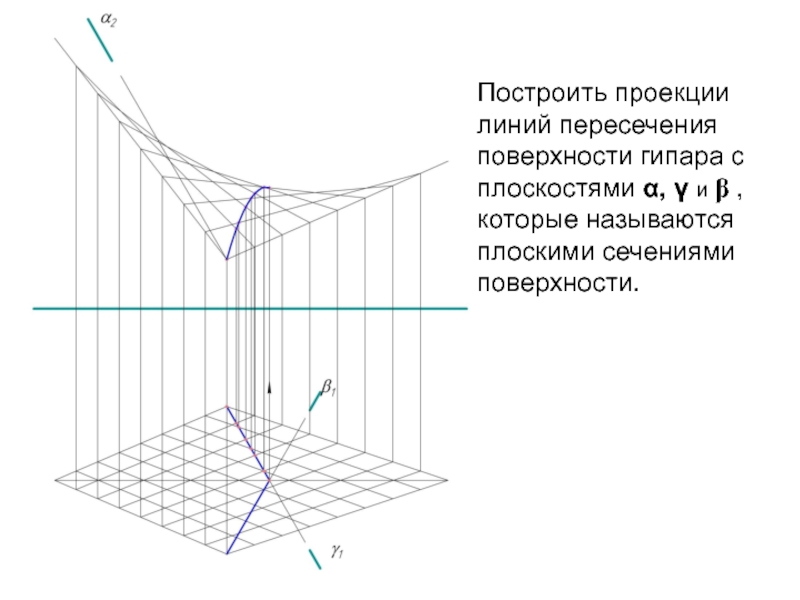
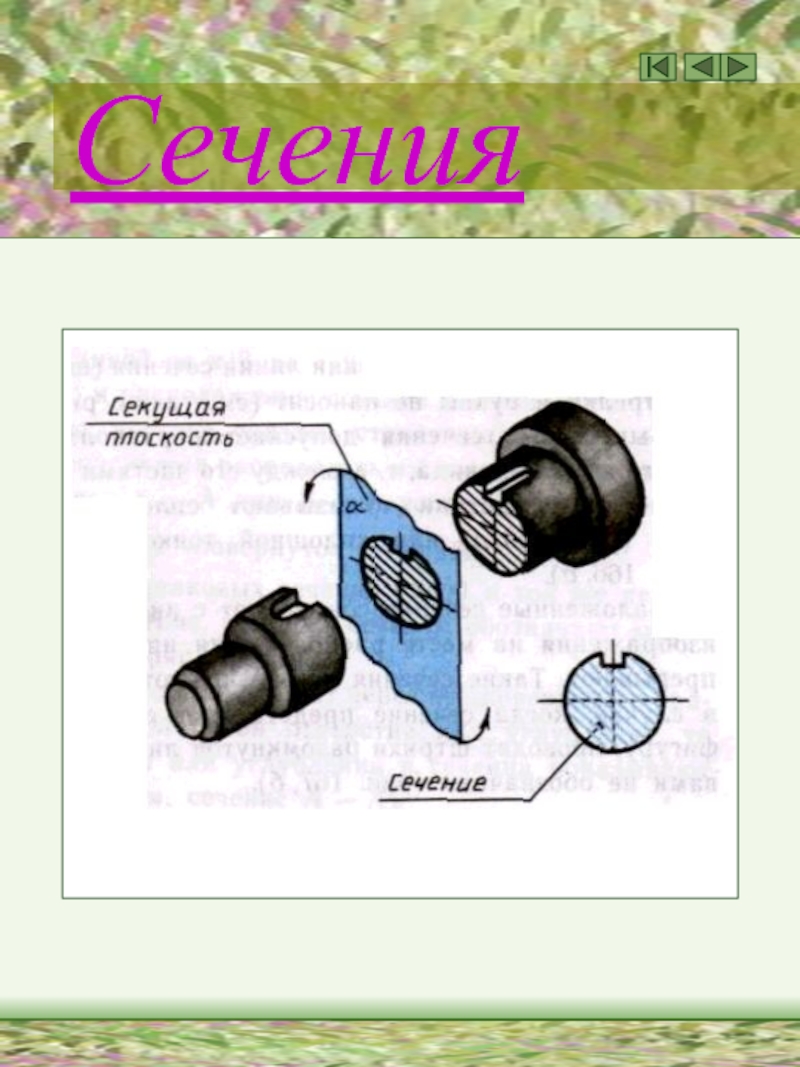
Слайд 8Построить проекции линий пересечения поверхности гипара с плоскостями α, γ и
β , которые называются плоскими сечениями поверхности.
Слайд 9Построить проекции линий пересечения поверхности гипара с плоскостями α, γ и
β , которые называются плоскими сечениями поверхности.
Сечение получаются ка совокупность точек пересечения образующих поверхности (каркасной сетки) гипара с данными проецирующими плоскостями.
Слайд 10Построить проекции линий пересечения поверхности гипара с плоскостями α, γ и
β , которые называются плоскими сечениями поверхности.
Сечение получаются ка совокупность точек пересечения образующих поверхности (каркасной сетки) гипара с данными проецирующими плоскостями.
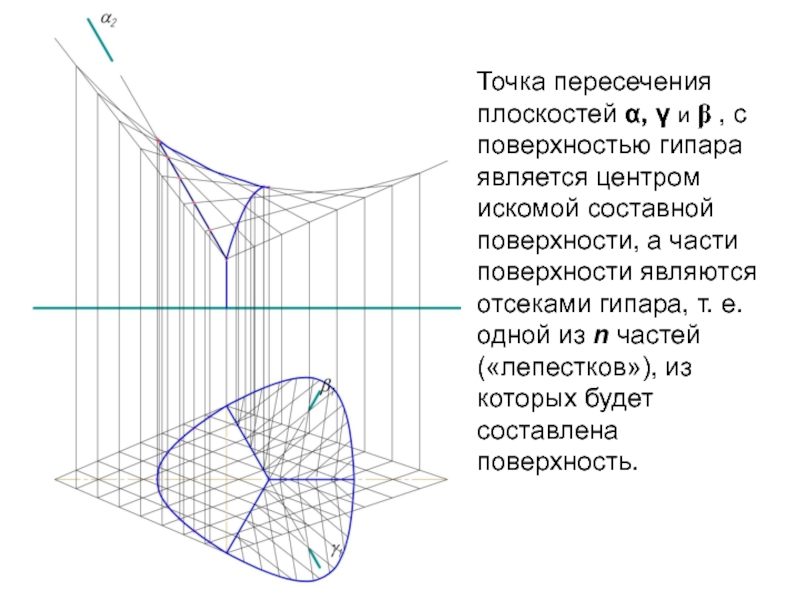
Слайд 11Точка пересечения плоскостей α, γ и β , с поверхностью гипара
является центром искомой составной поверхности, а части поверхности являются отсеками гипара, т. е. одной из n частей («лепестков»), из которых будет составлена поверхность.
Слайд 12План и фасад комбинированной поверхности гипаров выполняется как последовательное построение смежных
копий первого (исходного) отсека.
Каждая точка перемещается вокруг горизонталь-проецирующей оси вращения, следовательно на горизонтальной плоскости проекций мы видим перемещение по окружности, а на фронтальной плоскости проекций, по фронтально-проецирующему следу окружности (траектории перемещения точки).
Слайд 13Последовательно формируем границы отсеков с учетом их видимости. В результате все
лепестки и все проекции должны быть заполнены сетками образующих.
Слайд 15Последовательно построить семейства границ отсеков («лепестков») с последовательным построением всех образующих
в отсеках, формируемой поверхности.
