- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Комплексный чертеж плоскости. Плоскость на чертеже презентация
Содержание
- 1. Комплексный чертеж плоскости. Плоскость на чертеже
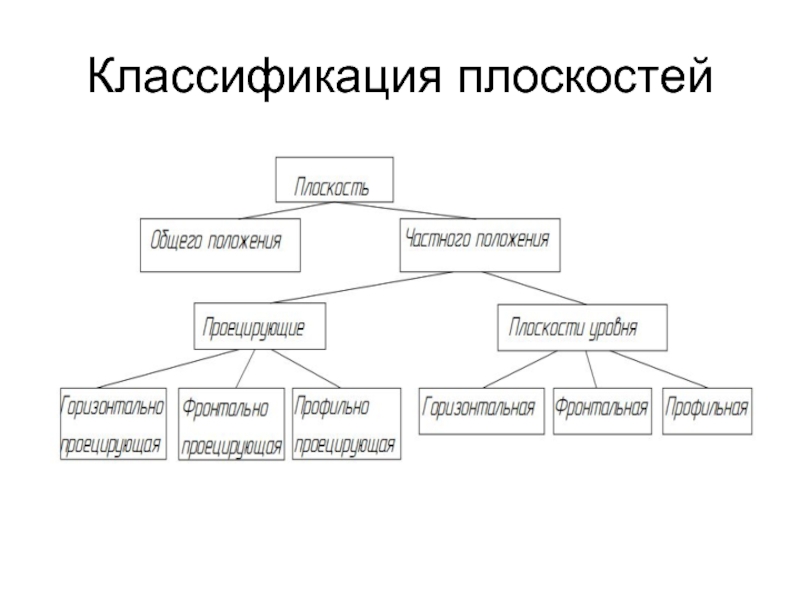
- 2. Классификация плоскостей
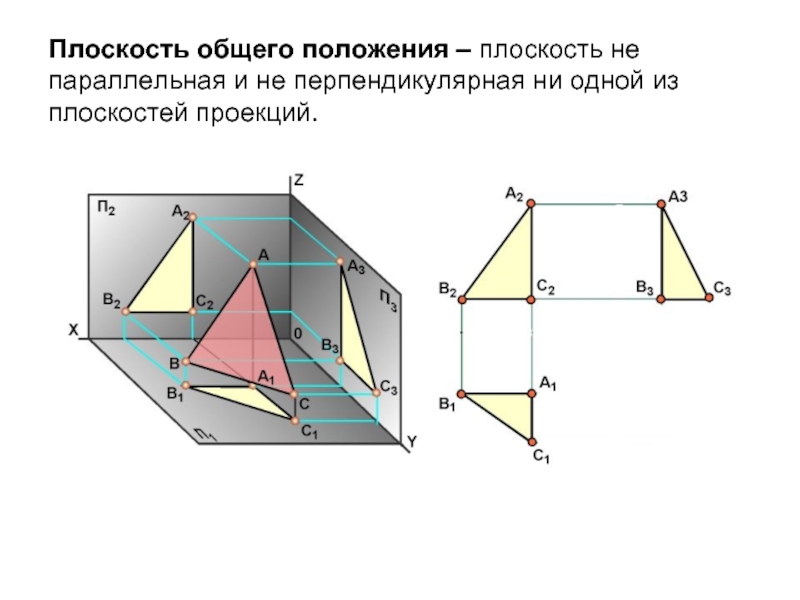
- 3. Плоскость общего положения – плоскость не параллельная и не перпендикулярная ни одной из плоскостей проекций.
- 4. Взаимная принадлежность точки, прямой и плоскости
- 5. Прямая принадлежит плоскости, если она: 1.
- 6. Плоскости частного положения Плоскости,
- 7. Горизонтально проецирующая плоскость Г ⊥⊥
- 8. Фронтально проецирующая плоскость - это плоскость, перпендикулярная
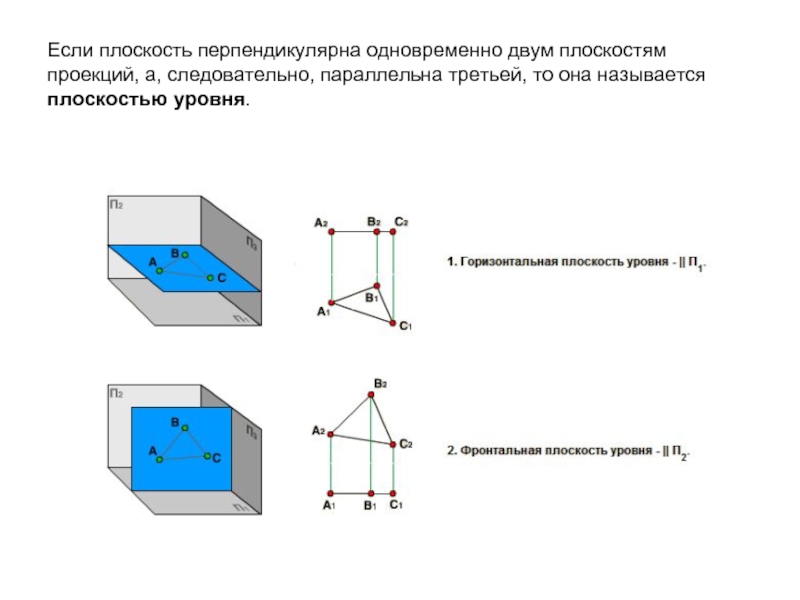
- 9. Если плоскость перпендикулярна одновременно двум плоскостям проекций,
- 10. Особые линии
- 11. Линии наибольшего наклона плоскости. 1.Прямая, лежащая в
- 12. 2.Прямая, лежащая в плоскости и перпендикулярная ее
- 13. Прямая, параллельная плоскости Прямая, // плоскости, если
- 14. Взаимно-параллельные плоскости. Плоскости взаимно параллельны, если
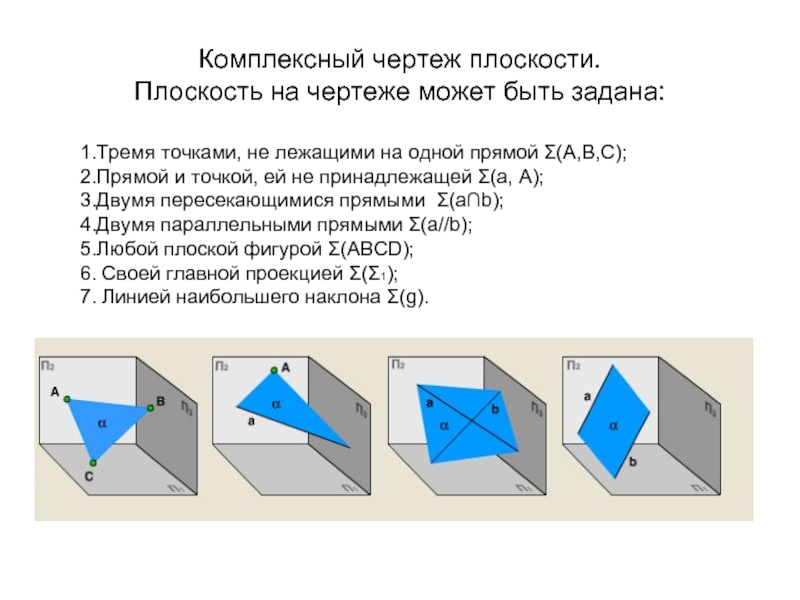
Слайд 1Комплексный чертеж плоскости.
Плоскость на чертеже может быть задана:
1.Тремя точками, не лежащими
2.Прямой и точкой, ей не принадлежащей Σ(а, А);
3.Двумя пересекающимися прямыми Σ(а∩b);
4.Двумя параллельными прямыми Σ(а//b);
5.Любой плоской фигурой Σ(АВСD);
6. Своей главной проекцией Σ(Σ1);
7. Линией наибольшего наклона Σ(g).
Слайд 3Плоскость общего положения – плоскость не параллельная и не перпендикулярная ни
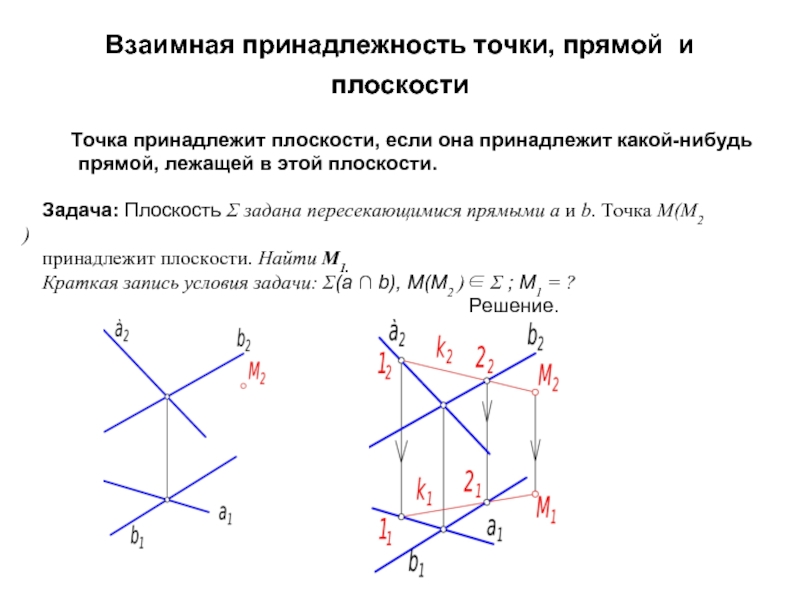
Слайд 4Взаимная принадлежность точки, прямой и плоскости
Точка принадлежит плоскости,
Задача: Плоскость Σ задана пересекающимися прямыми а и b. Точка М(М2 )
принадлежит плоскости. Найти М1.
Краткая запись условия задачи: Σ(а ∩ b), М(М2 )∈ Σ ; М1 = ?
Решение.
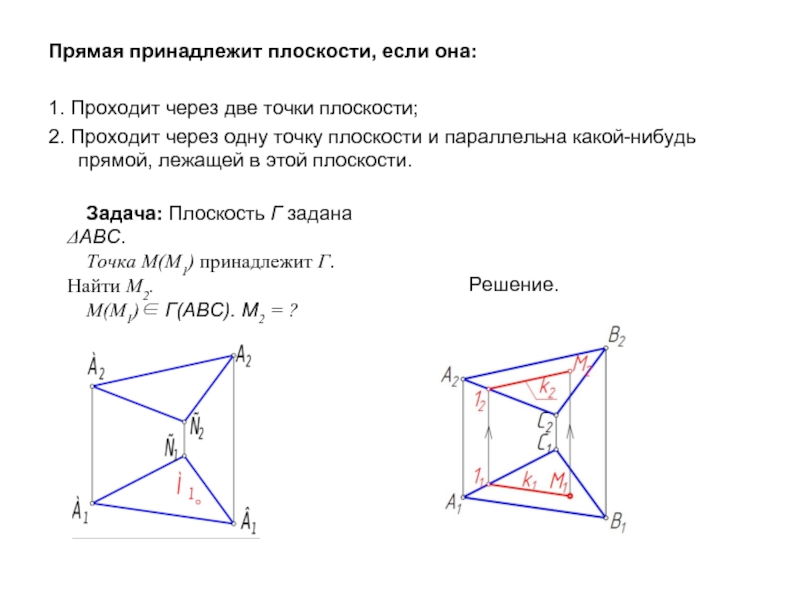
Слайд 5Прямая принадлежит плоскости, если она:
1. Проходит через две точки плоскости;
2. Проходит
Задача: Плоскость Г задана ΔАВС.
Точка М(М1) принадлежит Г. Найти М2.
М(М1)∈ Г(АВС). М2 = ?
Решение.
Слайд 6Плоскости частного положения
Плоскости, параллельные или перпендикулярные одной из плоскостей
К ним относятся:
Проецирующие плоскости
Плоскости уровня
Слайд 7
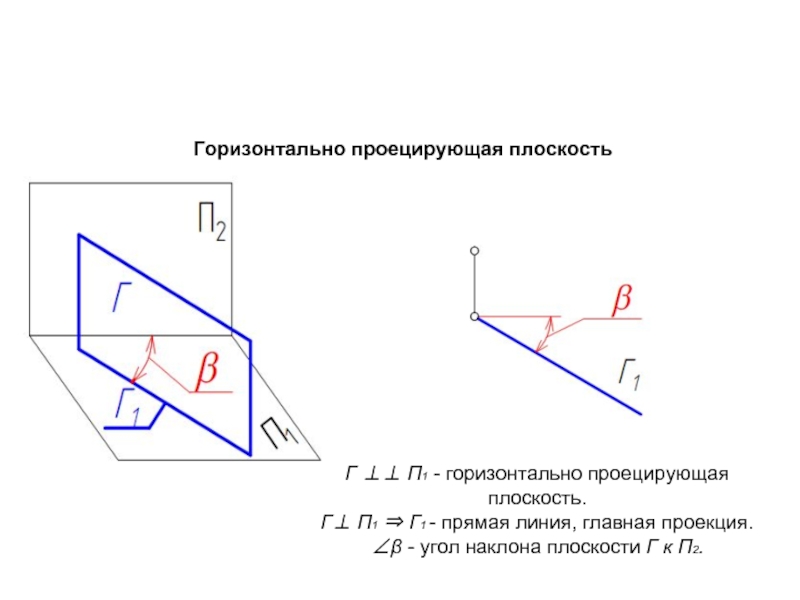
Горизонтально проецирующая плоскость
Г ⊥⊥ П1 - горизонтально проецирующая плоскость.
Г⊥ П1 ⇒
∠β - угол наклона плоскости Г к П2.
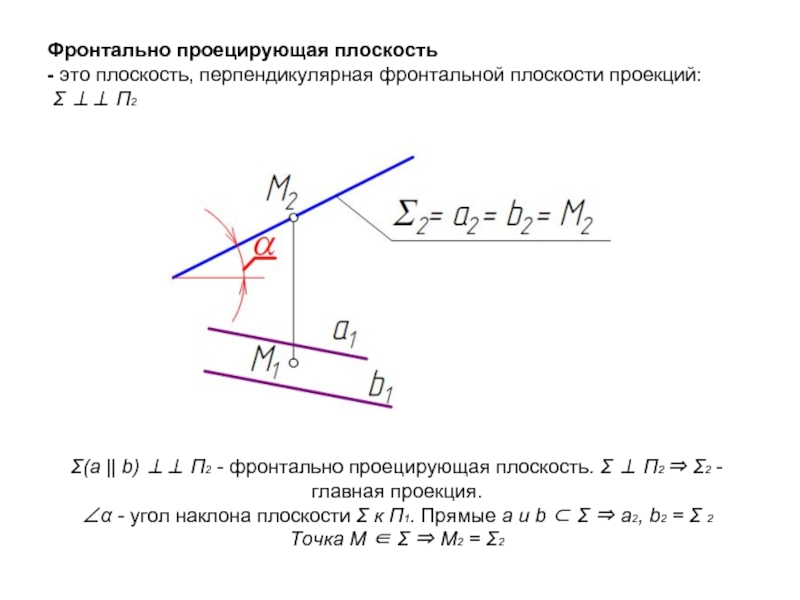
Слайд 8Фронтально проецирующая плоскость - это плоскость, перпендикулярная фронтальной плоскости проекций: Σ ⊥⊥
Σ(а || b) ⊥⊥ П2 - фронтально проецирующая плоскость. Σ ⊥ П2 ⇒ Σ2 - главная проекция.
∠α - угол наклона плоскости Σ к П1. Прямые а и b ⊂ Σ ⇒ а2, b2 = Σ 2
Точка М ∈ Σ ⇒ М2 = Σ2
Слайд 9Если плоскость перпендикулярна одновременно двум плоскостям проекций, а, следовательно, параллельна третьей,
Слайд 10 Особые линии плоскости
Линии уровня плоскости
h ⊂ Σ(АВС), h // П1.
Прямая, принадлежащая плоскости и параллельная фронтальной плоскости проекций, называется фронталью плоскости:
f ⊂ Σ(АВС), f // П2
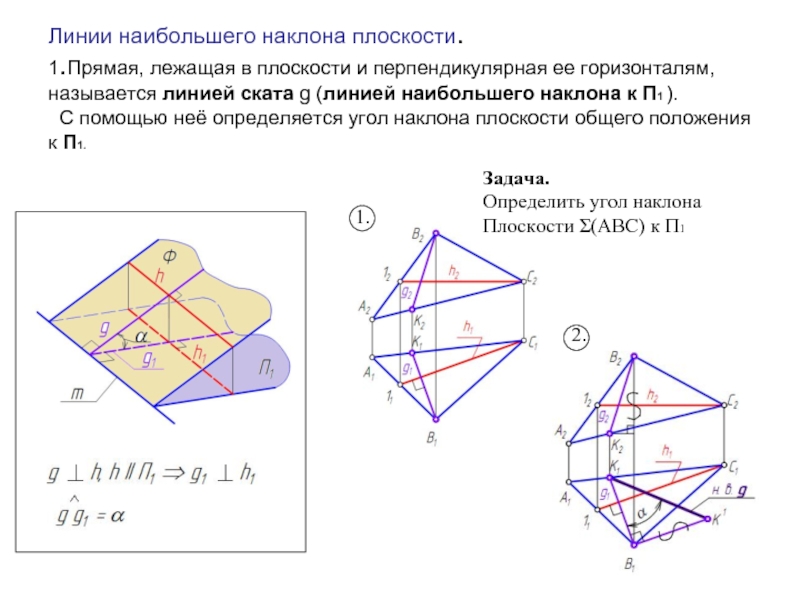
Слайд 11Линии наибольшего наклона плоскости. 1.Прямая, лежащая в плоскости и перпендикулярная ее горизонталям,
Задача.
Определить угол наклона
Плоскости Σ(АВС) к П1
2.
1.
Слайд 122.Прямая, лежащая в плоскости и перпендикулярная ее фронталям, называется линией наибольшего
С помощью неё определяется угол наклона плоскости общего положения к П2.
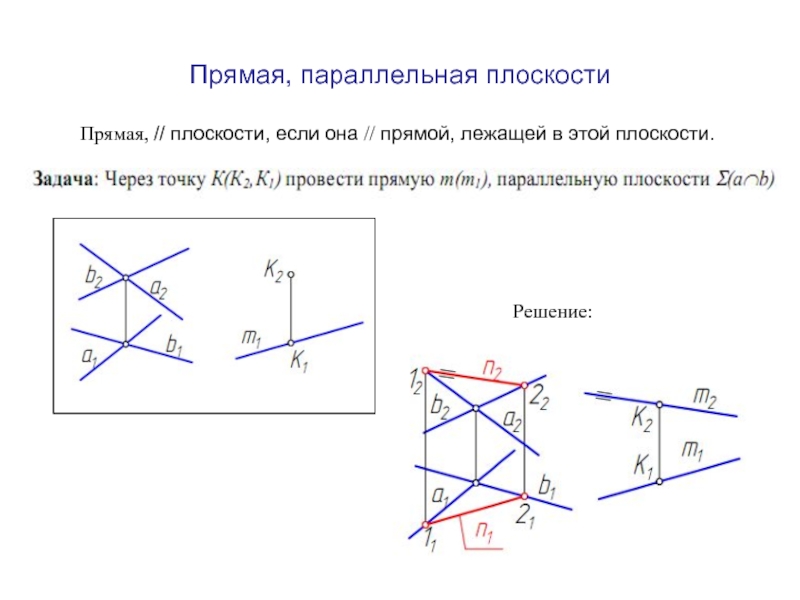
Слайд 13Прямая, параллельная плоскости
Прямая, // плоскости, если она // прямой, лежащей в
Решение:
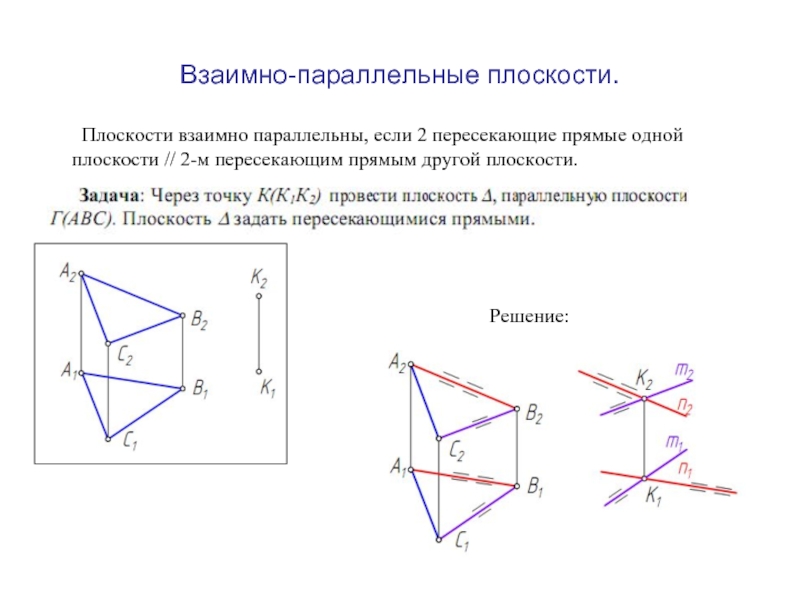
Слайд 14Взаимно-параллельные плоскости.
Плоскости взаимно параллельны, если 2 пересекающие прямые одной
плоскости //
Решение: