- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Классификация поверхностей. Развертки поверхностей презентация
Содержание
- 1. Классификация поверхностей. Развертки поверхностей
- 2. Поверхность как объект пространства Понятие «поверхность» в
- 3. Для задания поверхности на
- 4. Одна и та же поверхность может быть
- 5. Поверхность на чертеже задают проекциями геометрической части
- 6. Линейчатые поверхности: Развертывающиеся Неразвертывающиеся Нелинейчатые поверхности: С
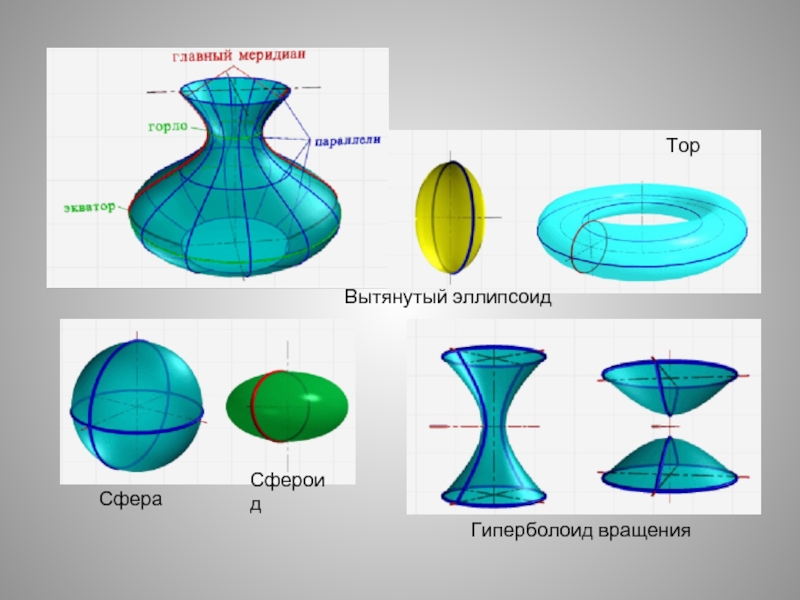
- 8. Гиперболоид вращения Сфера Сфероид Вытянутый эллипсоид Тор
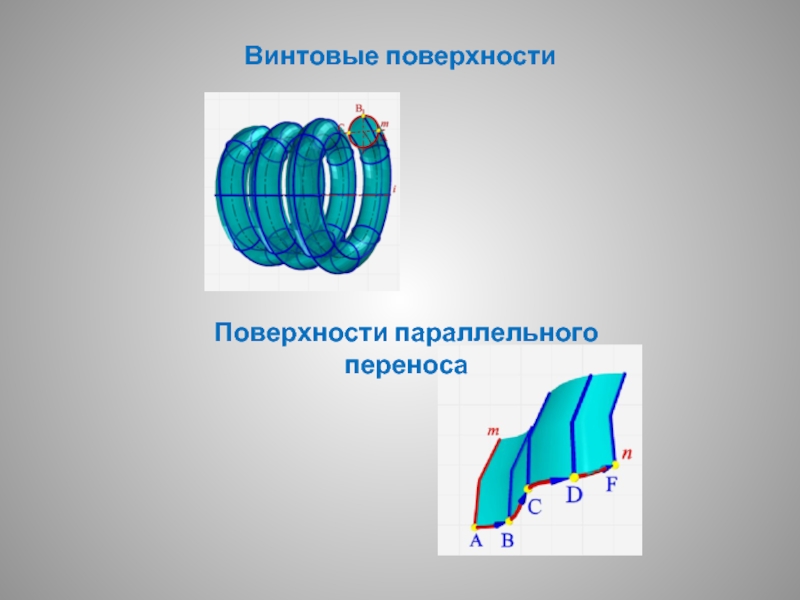
- 9. Винтовые поверхности Поверхности параллельного переноса
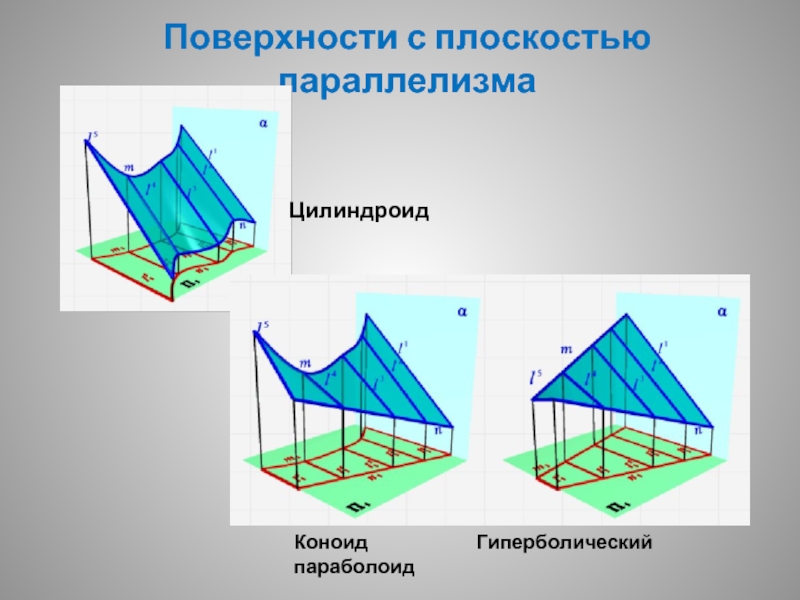
- 10. Поверхности с плоскостью
- 11. Задачи позиционные Задачи на
- 12. Точка и линия на поверхности Точка
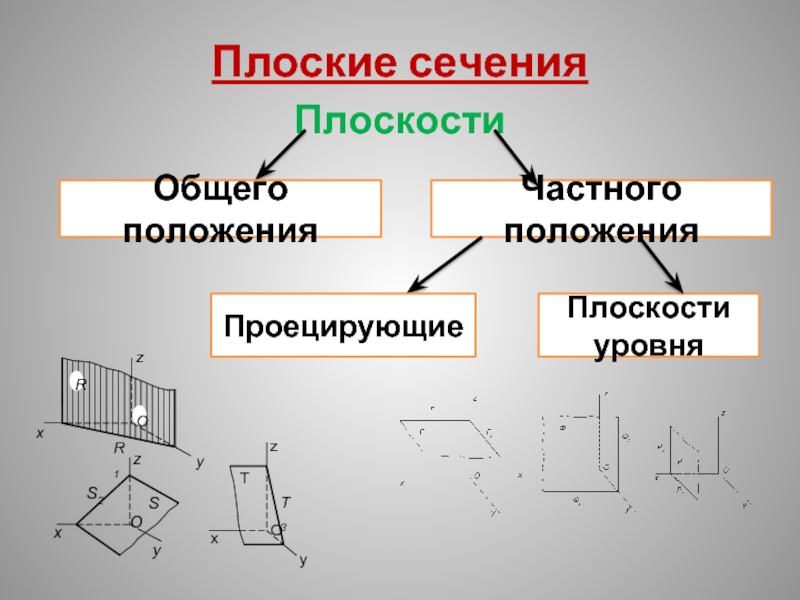
- 13. Плоские сечения Плоскости Общего положения Частного положения Проецирующие Плоскости уровня
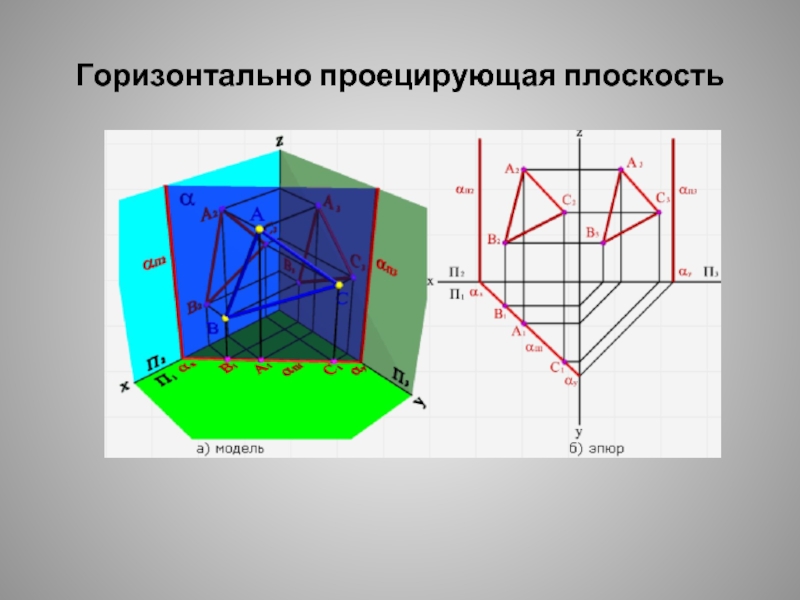
- 14. Горизонтально проецирующая плоскость
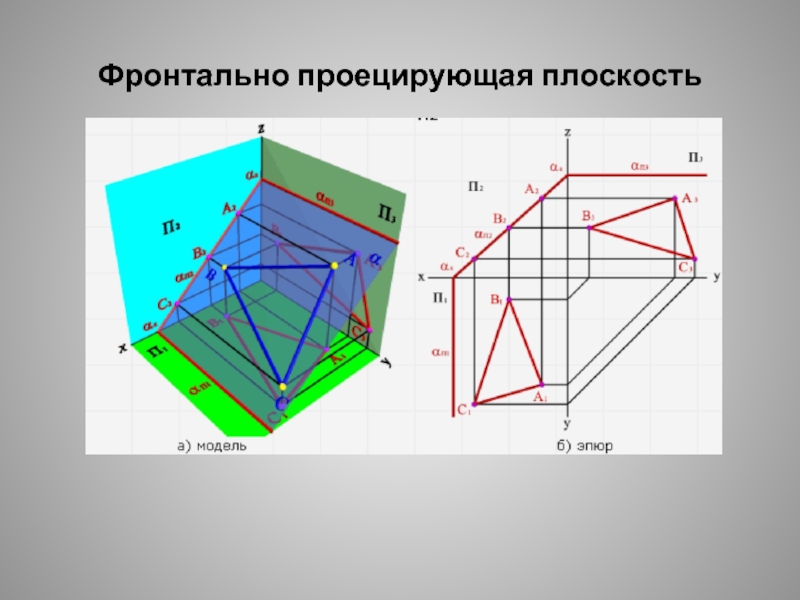
- 15. Фронтально проецирующая плоскость
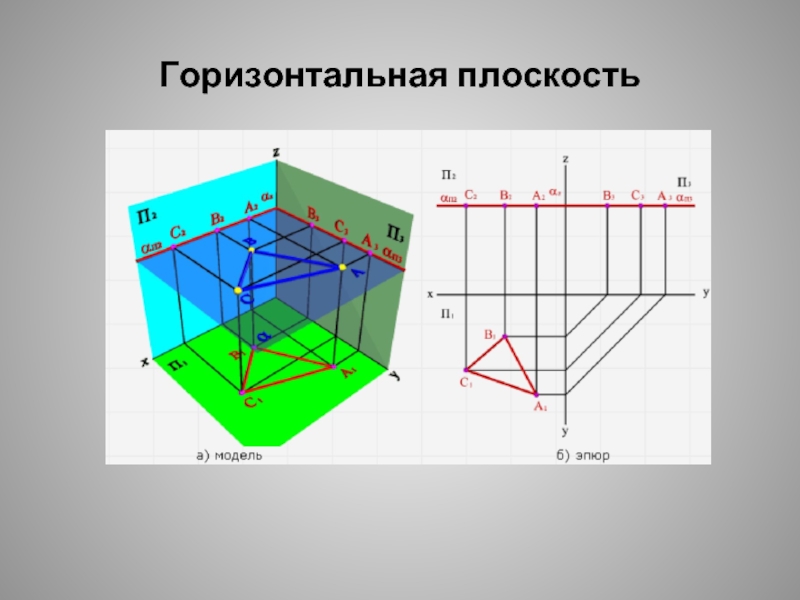
- 16. Горизонтальная плоскость
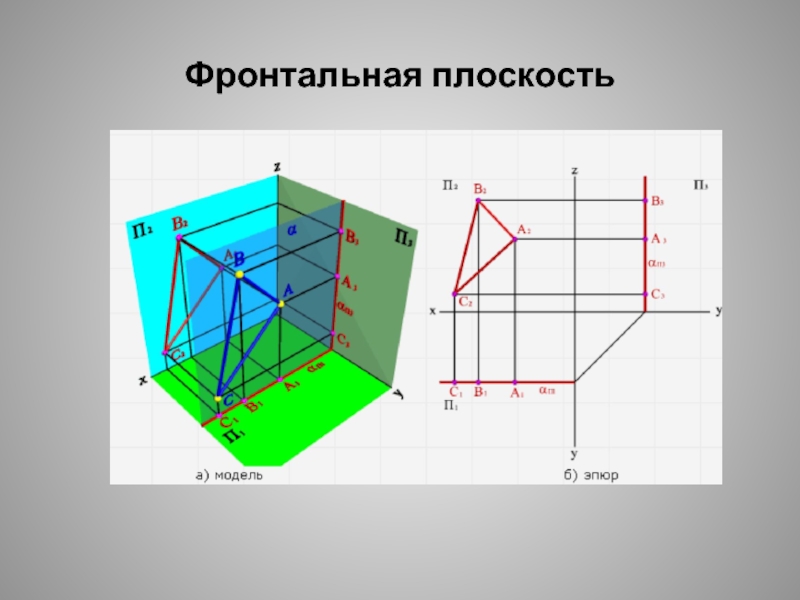
- 17. Фронтальная плоскость
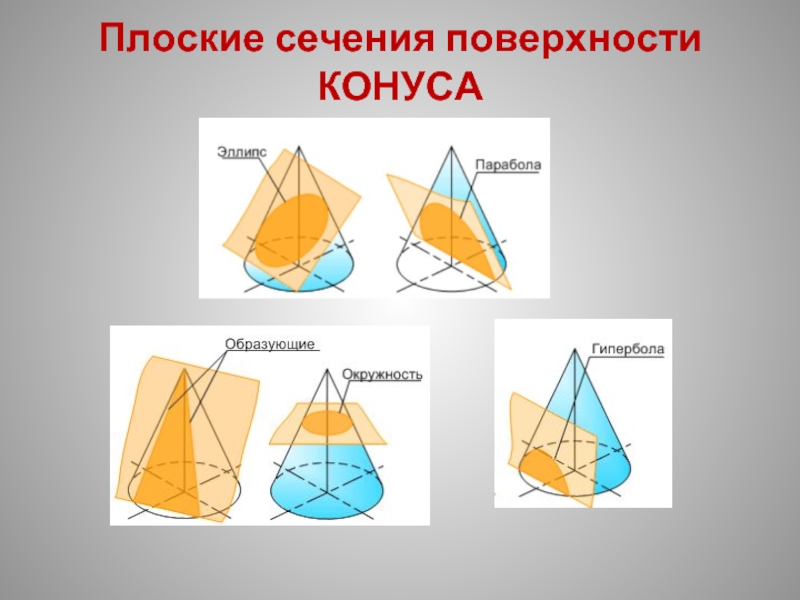
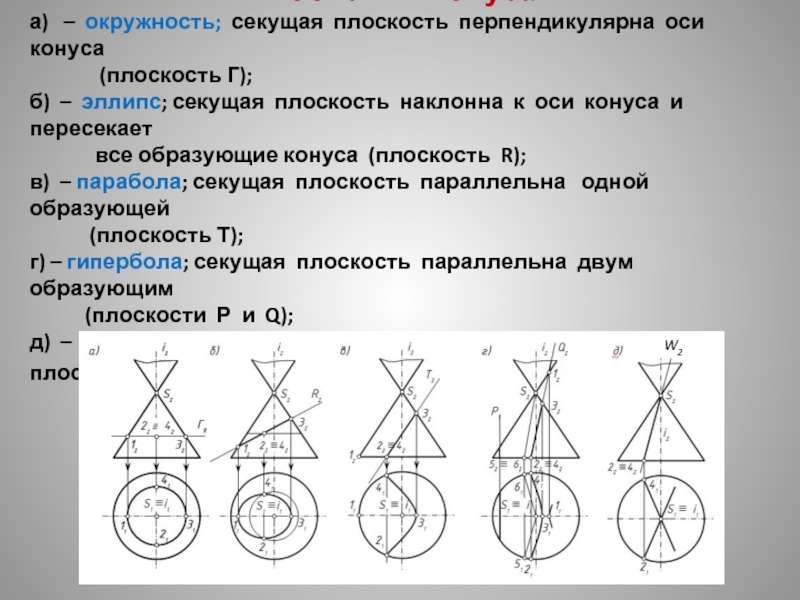
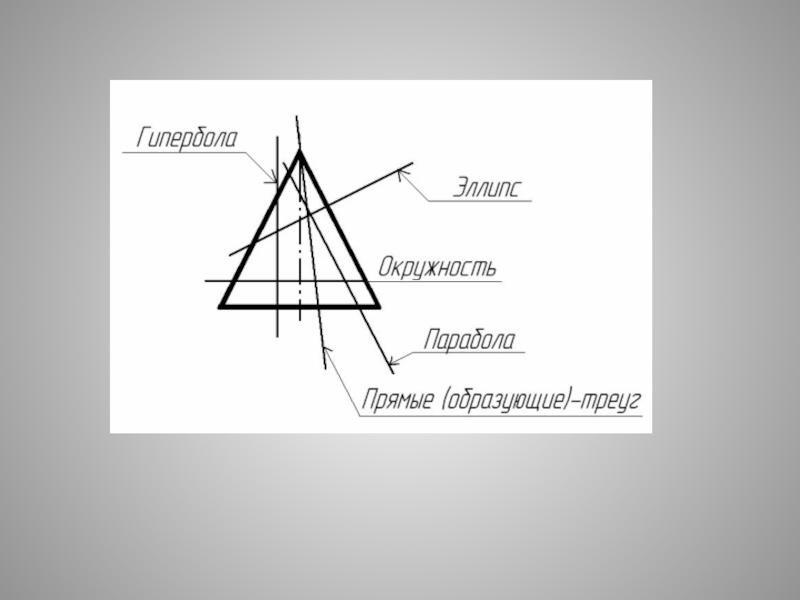
- 18. Плоские сечения поверхности КОНУСА
- 21. Задача Дана фронтальная проекция точки,
- 24. ПОСТРОЕНИЕ ЭЛЛИПСА ЭЛЛИПС – ДВАЖДЫ
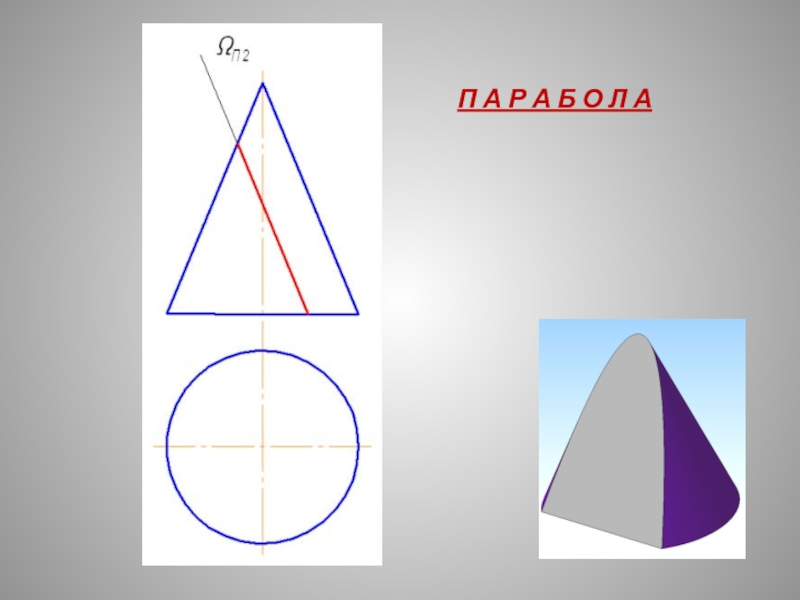
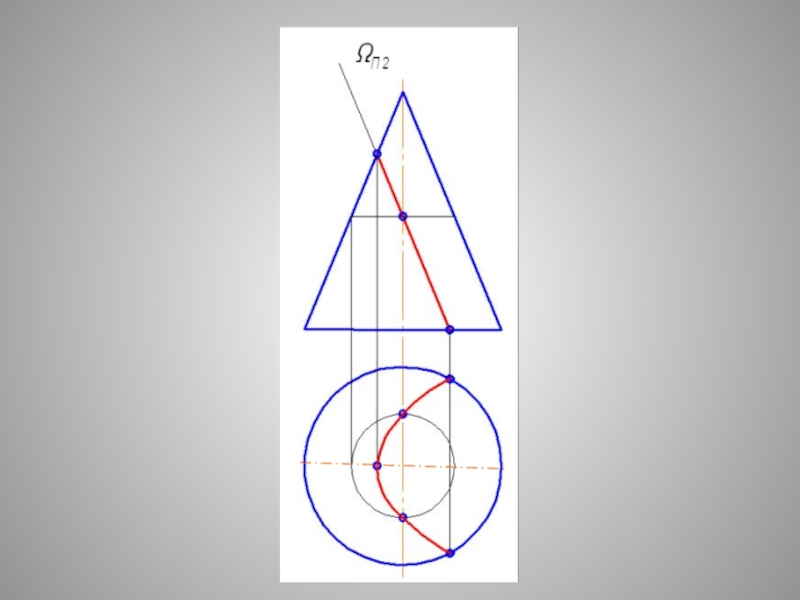
- 26. П А Р А Б О Л А
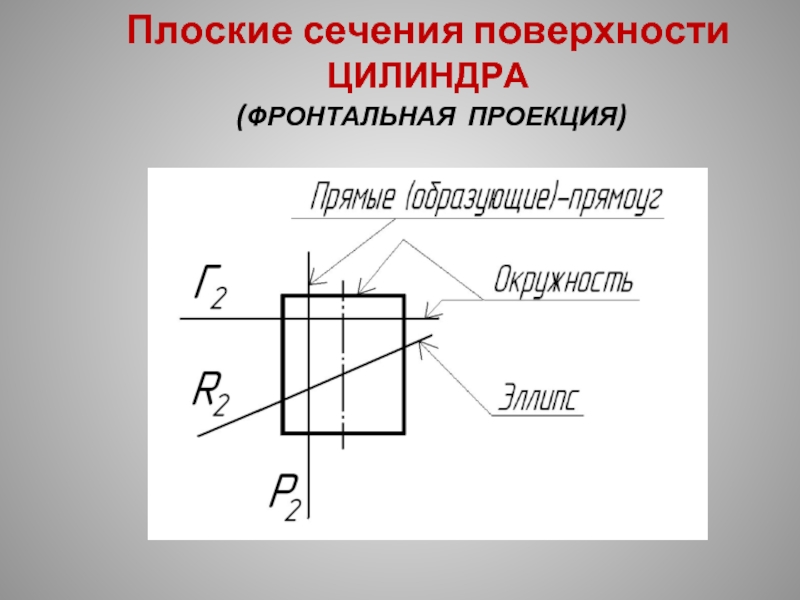
- 28. Плоские сечения поверхности ЦИЛИНДРА (ФРОНТАЛЬНАЯ ПРОЕКЦИЯ)
- 29. СЕЧЕНИЕ СФЕРЫ - ОКРУЖНОСТЬ ПРИ ЛЮБОМ
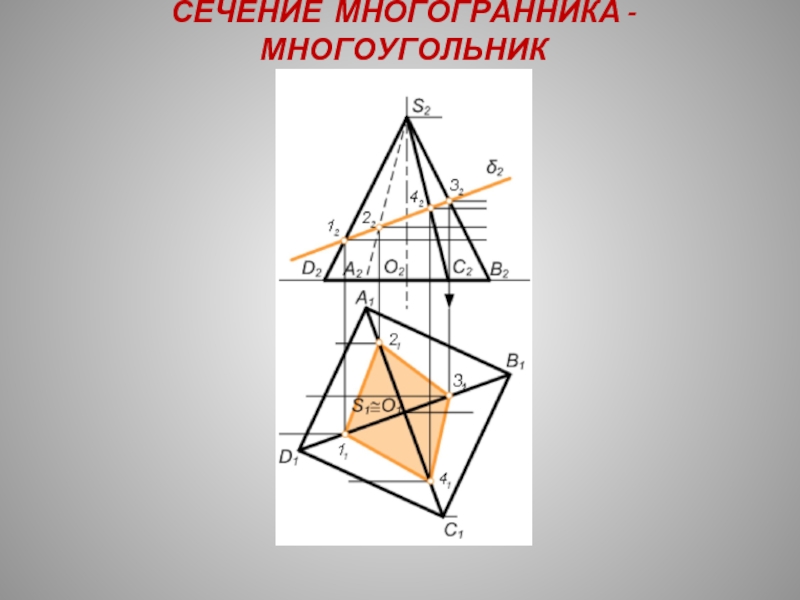
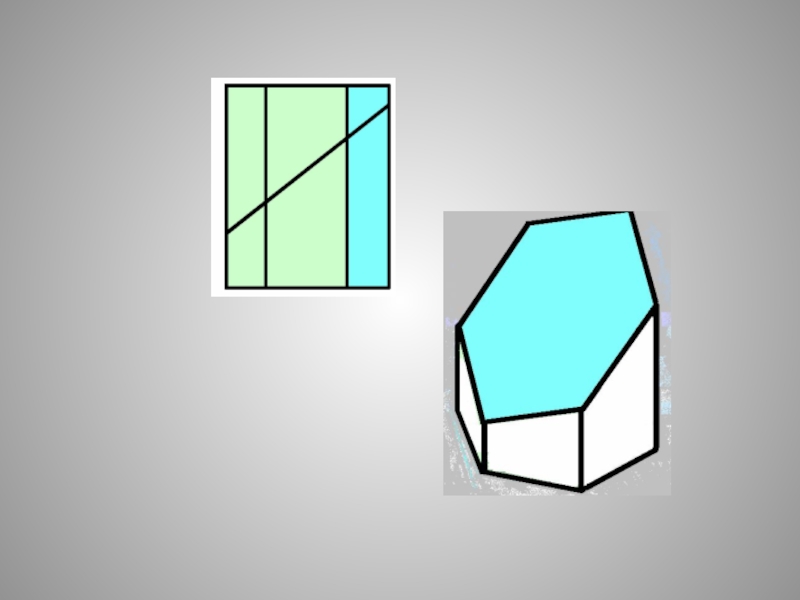
- 40. СЕЧЕНИЕ МНОГОГРАННИКА - МНОГОУГОЛЬНИК
Слайд 1 «Инженерная графика»
Слайд 2Поверхность как объект пространства Понятие «поверхность» в начертательной геометрии связано с представлением
Подвижная линия l называется образующей;
Неподвижная m, n, p, задающая направление перемещения, –
направляющей.
Слайд 3 Для задания поверхности на чертеже выбирают такую совокупность
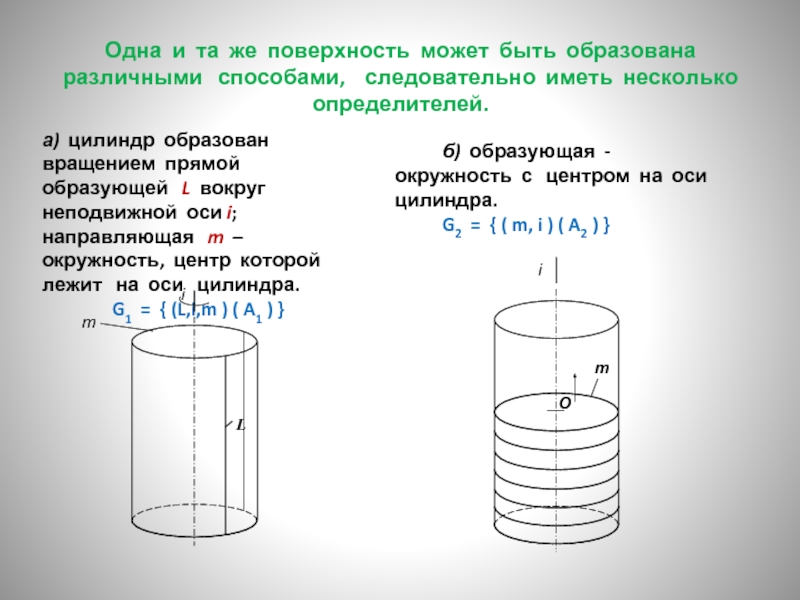
Слайд 4Одна и та же поверхность может быть образована различными способами,
а) цилиндр образован вращением прямой образующей L вокруг неподвижной оси i; направляющая m – окружность, центр которой лежит на оси цилиндра.
G1 = { (L,i,m ) ( A1 ) }
б) образующая - окружность с центром на оси цилиндра.
G2 = { ( m, i ) ( A2 ) }
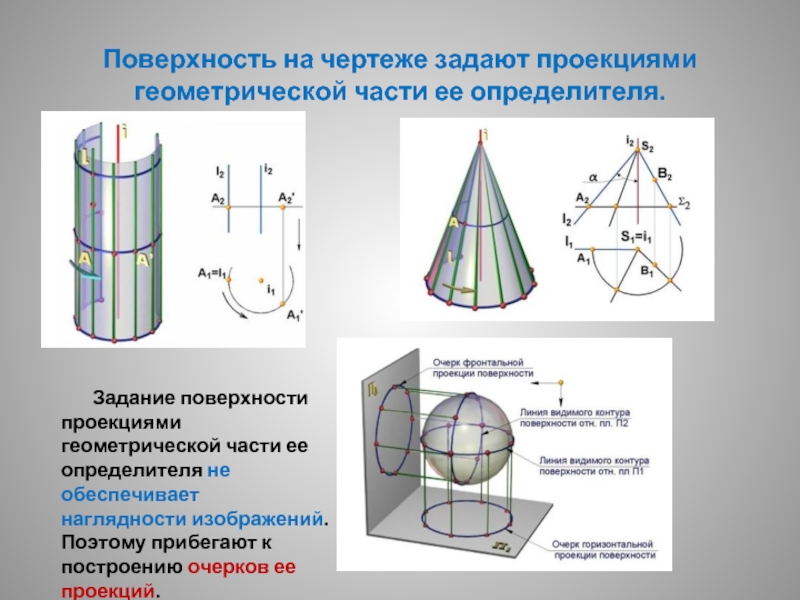
Слайд 5Поверхность на чертеже задают проекциями геометрической части ее определителя.
Слайд 6Линейчатые поверхности:
Развертывающиеся
Неразвертывающиеся
Нелинейчатые поверхности:
С образующей постоянной формы
(поверхности вращения и трубчатые пов-ти)
С
(циклические пов-ти)
Циклическая поверхность
Классификация поверхностей
При классификации поверхностей основополагающим является способ образования и свойства поверхности.
По виду образующей:
Линейчатые (образующая – прямая линия)
Нелинейчатые (образующая – кривая линия)
Слайд 7
Слайд 11
Задачи позиционные
Задачи на взаимную принадлежность геометрических образов
Задачи на взаимное пересечение геометрических
Слайд 12
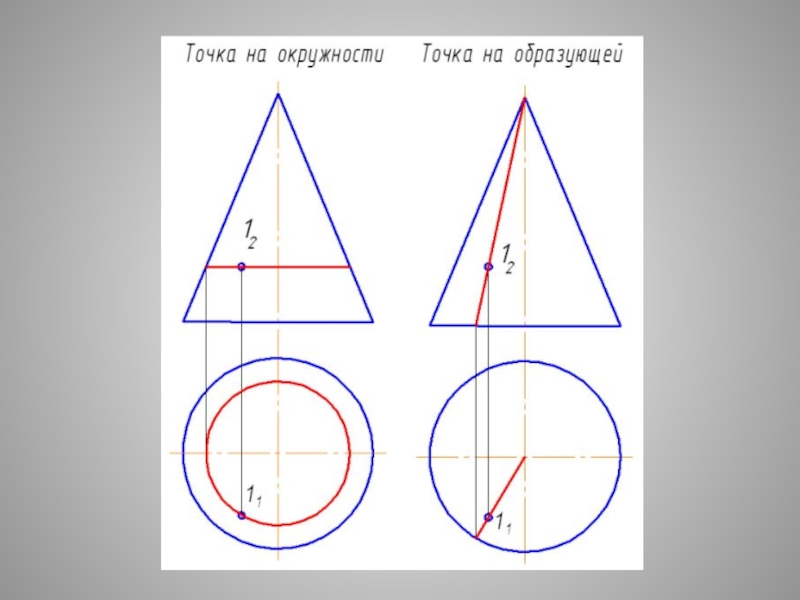
Точка и линия на поверхности
Точка принадлежит плоскости, если она принадлежит прямой,
Точка принадлежит поверхности, если она принадлежит линии, лежащей в данной поверхности.
Прямая принадлежит плоскости, если она имеет с ней две общие точки
Линия принадлежит поверхности, если имеет с ней n-ное количество общих точек.
Слайд 19
W2
Слайд 21
Задача
Дана фронтальная проекция точки, принадлежащей поверхности конуса.
Построить ее горизонтальную проекцию.
Диаметр основания
Высота конуса – 70 мм.
Слайд 23
АЛГОРИТМ
ПОВЕРХНОСТИ ВРАЩЕНИЯ 1. ВЫПОЛНИТЬ АНАЛИЗ УСЛОВИЯ: ОПРЕДЕЛИТЬ ФИГУРУ СЕЧЕНИЯ. 2. ПОСТРОИТЬ ХАРАКТЕРНЫЕ ТОЧКИ; ТОЧКИ ОБОЗНАЧИТЬ. 3. ПОСТРОИТЬ ДОПОЛНИТЕЛЬНЫЕ ТОЧКИ. 4. ВСЕ ПОЛУЧЕННЫЕ ТОЧКИ СОЕДИНИТЬ ПЛАВНОЙ КРИВОЙ С УЧЕТОМ ВИДИМОСТИ. ГЕОМЕТРИЧЕСКОЕ ТЕЛО считать
Н Е П Р О З Р А Ч Н Ы М.
Слайд 24
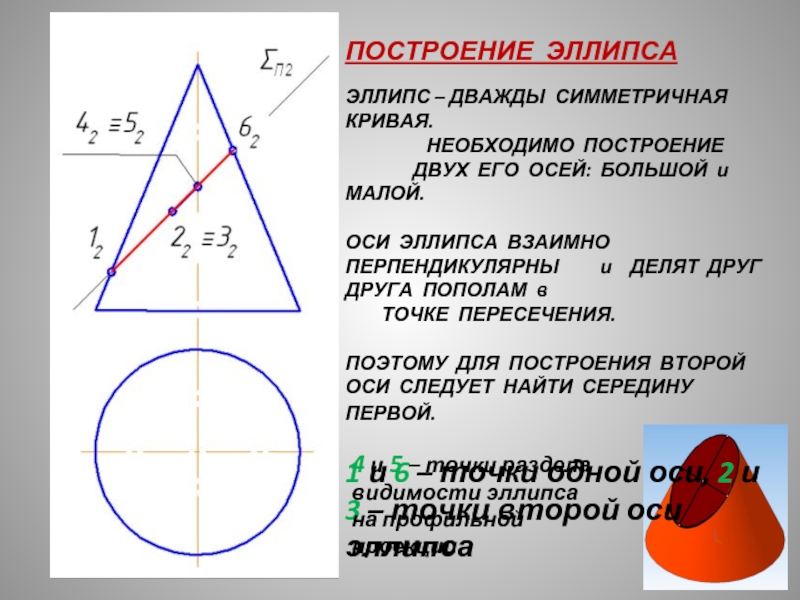
ПОСТРОЕНИЕ ЭЛЛИПСА
ЭЛЛИПС – ДВАЖДЫ СИММЕТРИЧНАЯ КРИВАЯ.
ДВУХ ЕГО ОСЕЙ: БОЛЬШОЙ и МАЛОЙ.
ОСИ ЭЛЛИПСА ВЗАИМНО ПЕРПЕНДИКУЛЯРНЫ и ДЕЛЯТ ДРУГ ДРУГА ПОПОЛАМ в ТОЧКЕ ПЕРЕСЕЧЕНИЯ. ПОЭТОМУ ДЛЯ ПОСТРОЕНИЯ ВТОРОЙ ОСИ СЛЕДУЕТ НАЙТИ СЕРЕДИНУ ПЕРВОЙ.
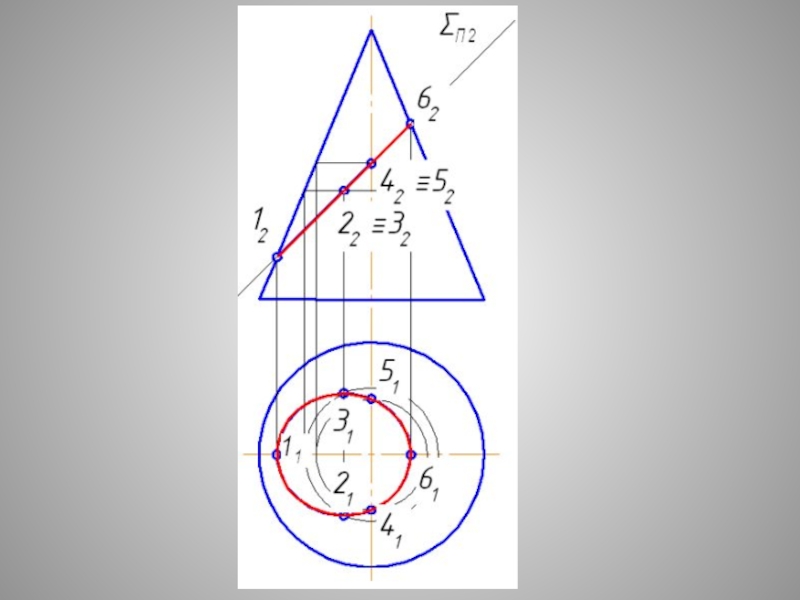
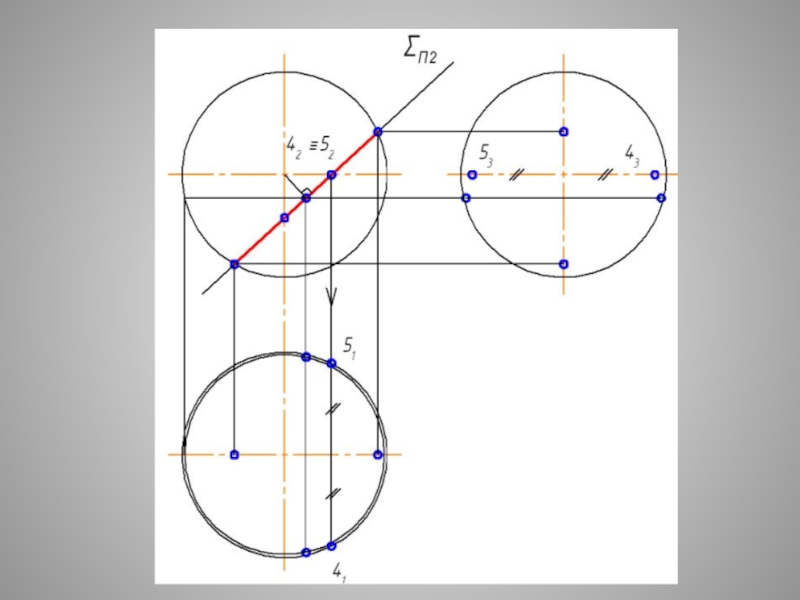
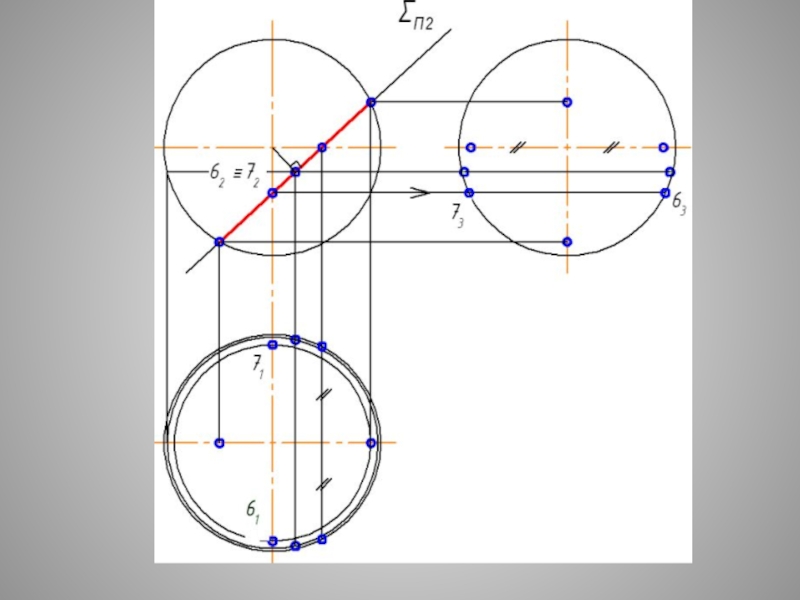
1 и 6 – точки одной оси, 2 и 3 – точки второй оси эллипса
4 и 5 – точки раздела видимости эллипса на профильной проекции
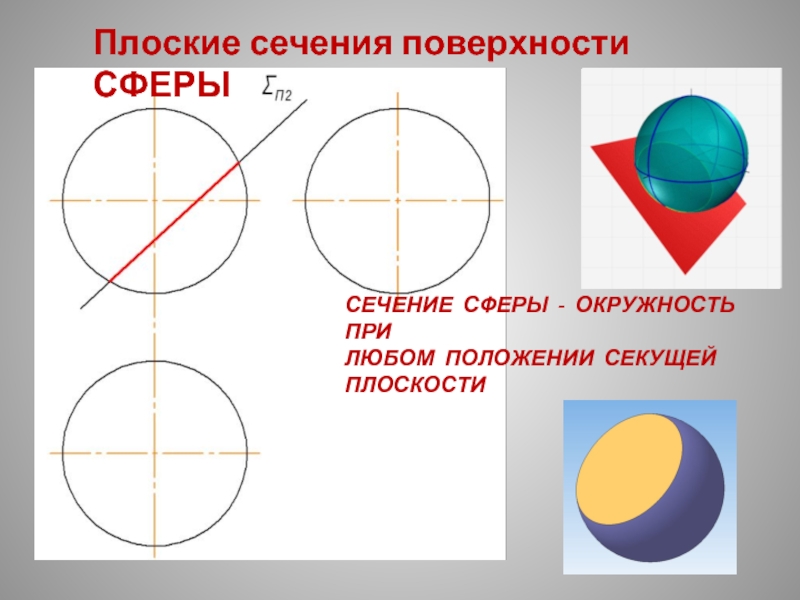
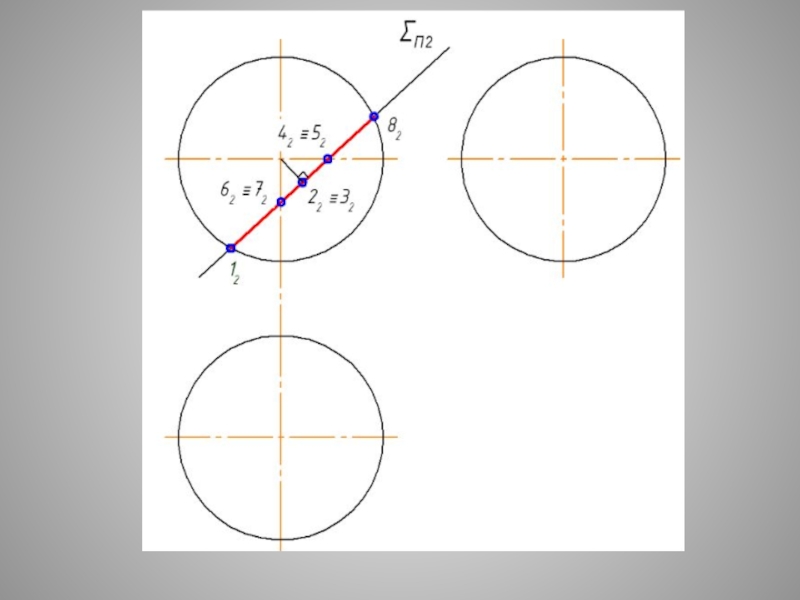
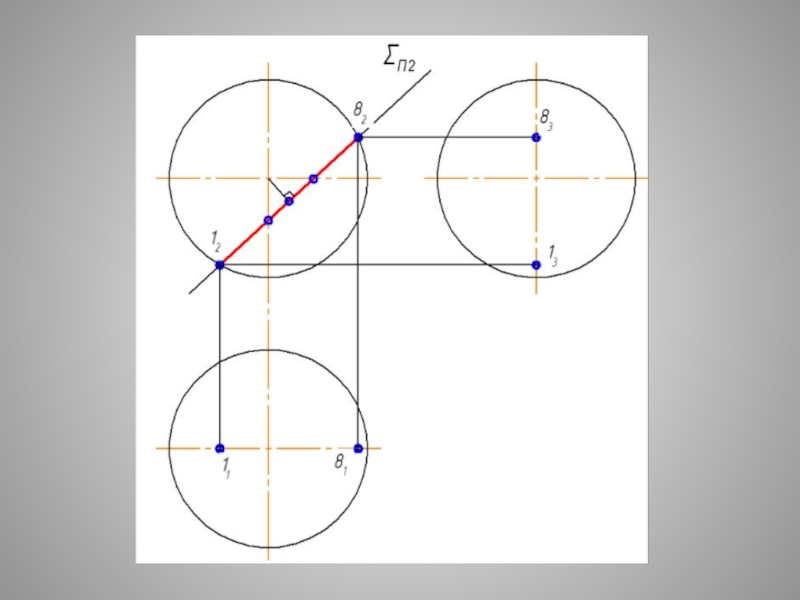
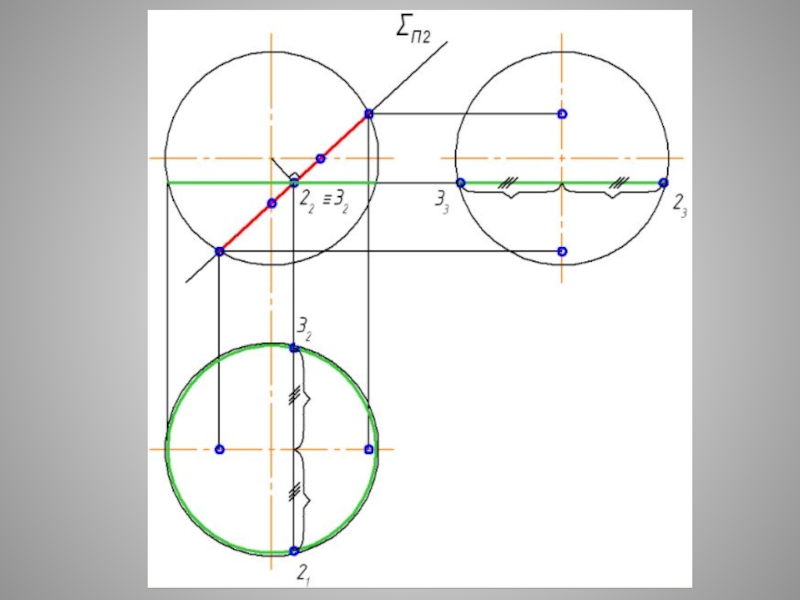
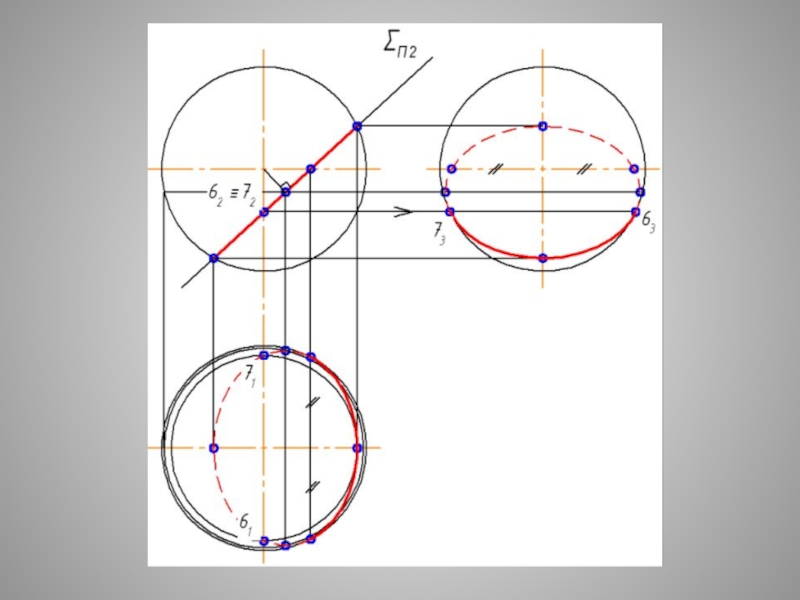
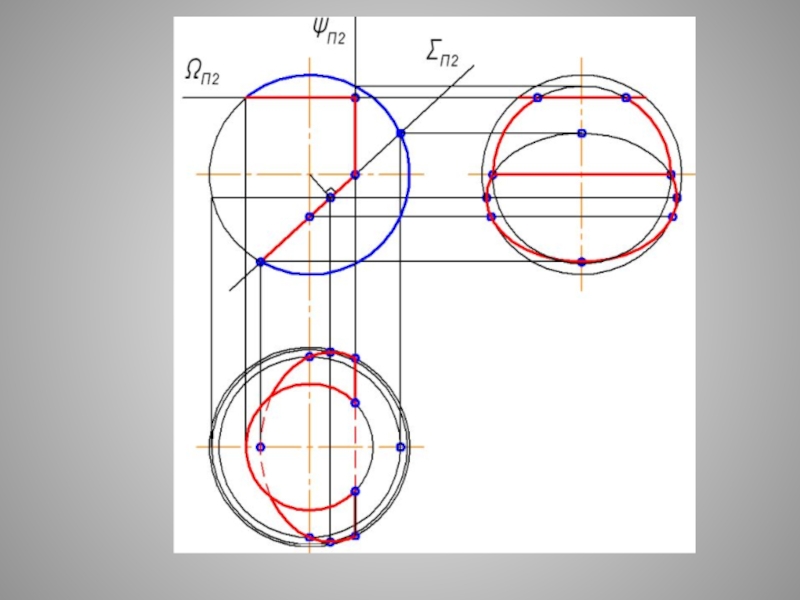
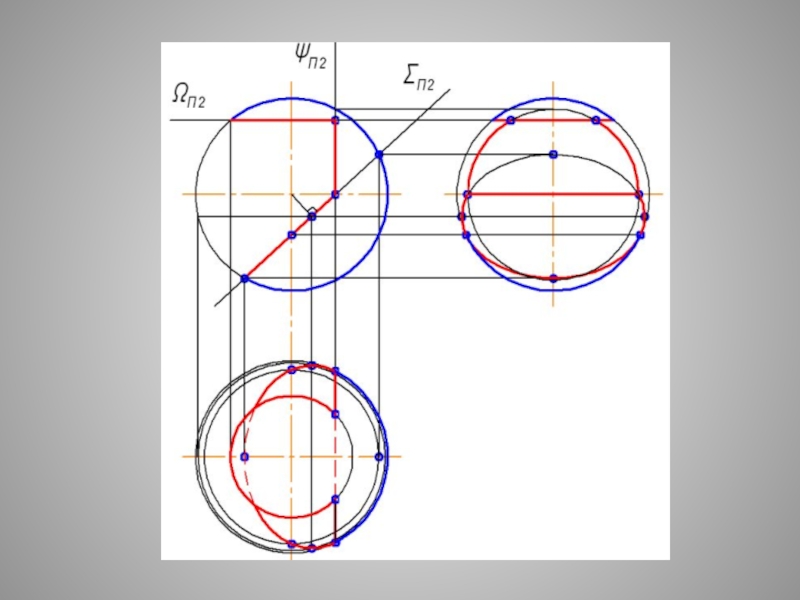
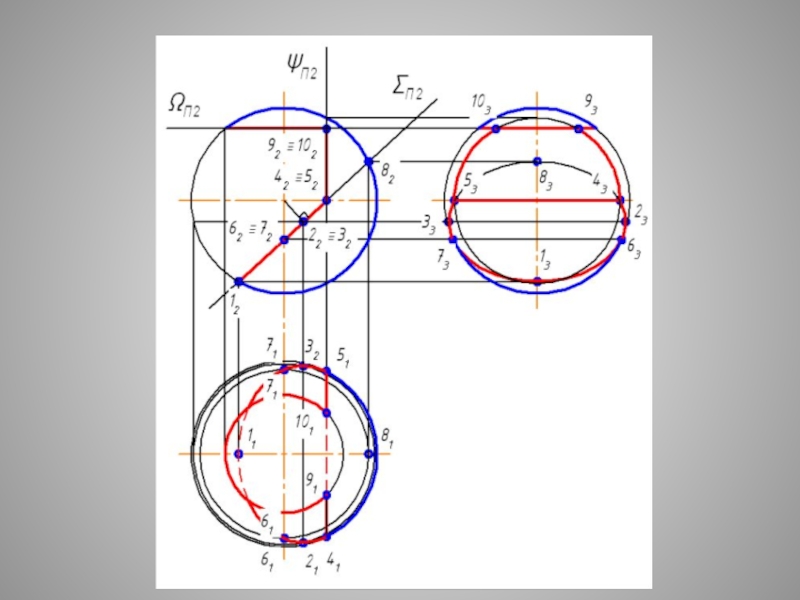
Слайд 29СЕЧЕНИЕ СФЕРЫ - ОКРУЖНОСТЬ ПРИ ЛЮБОМ ПОЛОЖЕНИИ СЕКУЩЕЙ
Плоские сечения поверхности СФЕРЫ
Слайд 39 АЛГОРИТМ ПОСТРОЕНИЯ ПРОЕКЦИЙ ТЕЛА