- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
ANSYS в инженерных задачах презентация
Содержание
- 1. ANSYS в инженерных задачах
- 2. Система уравнений Навье-Стокса Уравнение неразрывности (сохранения массы) Уравнение количества движения (сохранения импульса)
- 3. Система уравнений Навье-Стокса Уравнение энергии (сохранения энергии)
- 4. Анализ системы уравнений Навье-Стокса дифференциальные уравнения в
- 5. за решение Математический институт Клэя назначил премию
- 6. 10 января 2014 года математик Мухтарбай Отелбаев
- 7. Пример точного решения Течение Пуазейля ламинарное
- 8. Структура численного решения Дискретизация метод
- 9. Метод конечных объёмов Уравнение неразрывности и количества
- 10. Дискретная форма интегральных соотношений Метод конечных
- 11. В МКО заложено точное интегральное сохранение таких
- 12. Шаг по времени и невязки Шаг по
- 13. Уравнения Рейнольдса - напряжения Рейнольдса Уравнения Навье-Стокса, осреднённые по Рейнольдсу
- 14. Модели турбулентности Модели вихревой вязкости: Однопараметрическая модель
- 15. Алгебраические модели Алгебраические модели - это простейший
- 16. Турбулентная вязкость по физическому смыслу аналогична формуле
- 17. Модели с одним уравнением Кинетическая энергия единицы
- 18. Обтекание обращённой назад ступеньки Сравнение эксперимента и расчёта турбулентного обтекания автомобиля Модели с двумя уравнениями
- 19. Модели турбулентности В общем виде, используемые в
- 20. В случае SST модели последний член уравнения
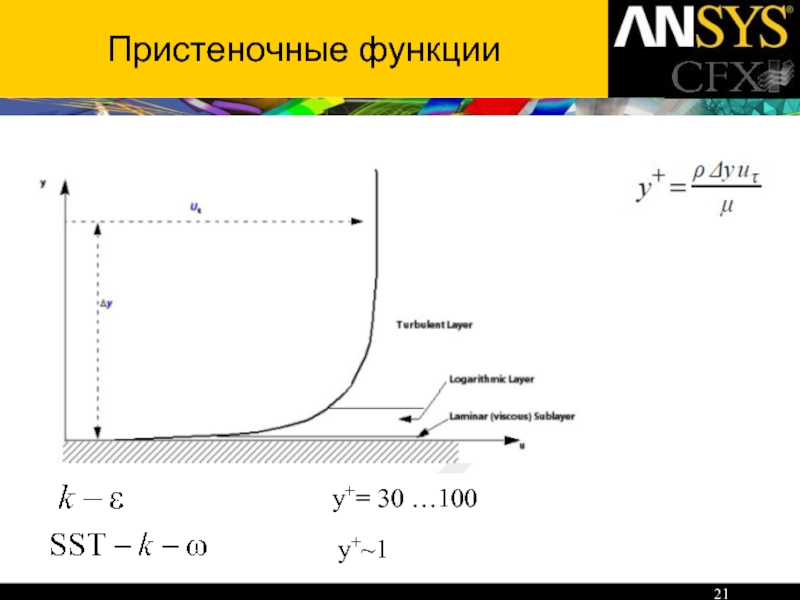
- 21. Пристеночные функции y+= 30 …100 y+~1
- 22. Цикл проектирования и анализа Создание геометрической модели
- 23. Архитектура комплекса ANSYS CFX CFX-Pre (Препроцессор физики)
- 24. CAD Система автоматизации проектных работ (САПР) или
- 25. CAD В ANSYS CFX могут импортироваться геометрические
- 26. Комплекс ANSYS CFX 1. ANSYS CFX-Pre –
- 27. CFX Mesh CFX Mesh – приложение генерации
- 28. ANSYS ICEM CFD ANSYS ICEM CFD -
- 29. ANSYS CFX-Pre Физический препроцессор ANSYS CFX-Pre импортирует
- 30. ANSYS CFX-Pre ANSYS CFX-Pre реализует процесс определения
- 31. ANSYS CFX-Solver Решатель ANSYS CFX - Solver
- 32. ANSYS CFX-Solver ANSYS CFX - Solver реализует
- 33. ANSYS CFX-Post Постпроцессор ANSYS CFX-Post предназначен для
- 34. ANSYS Workbench ANSYS Workbench входит в состав
- 35. ANSYS Workbench ANSYS Workbench включает следующие приложения:
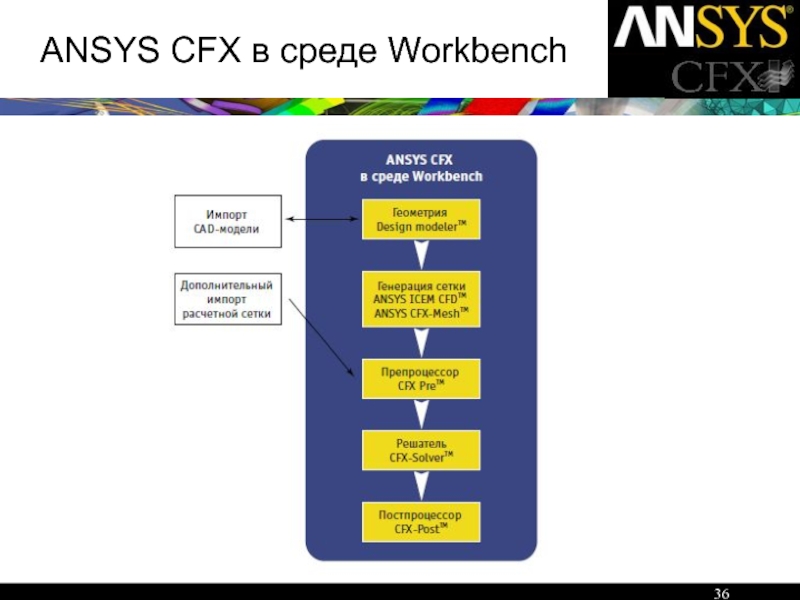
- 36. ANSYS CFX в среде Workbench
- 37. Области применения Аэрокосмическая промышленность: процессы обтекания тел,
- 38. Список источников Ландау Л.Д., Лифшиц Е.М. Механика
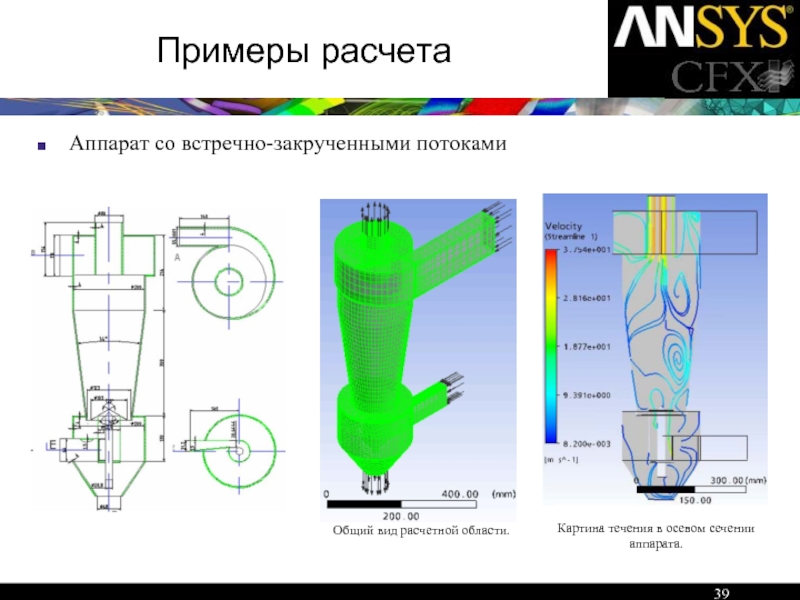
- 39. Примеры расчета Аппарат со встречно-закрученными потоками
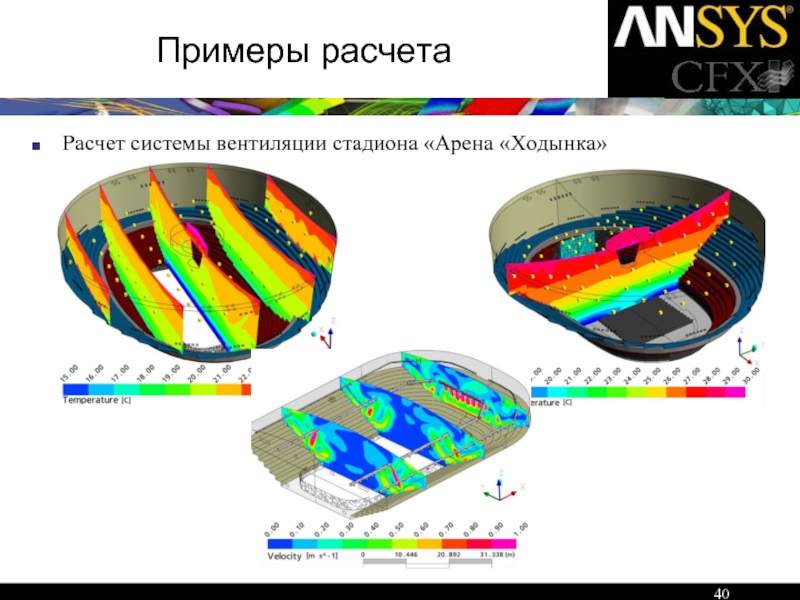
- 40. Примеры расчета Расчет системы вентиляции стадиона «Арена «Ходынка»
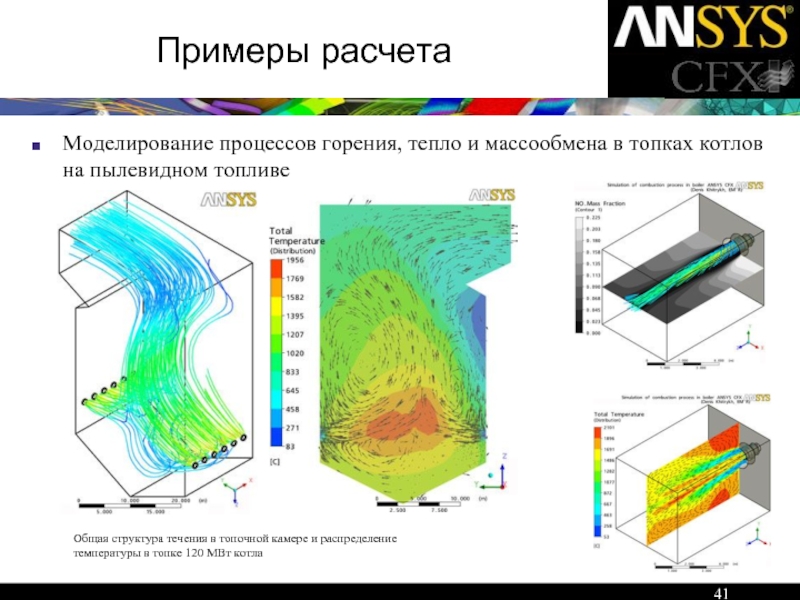
- 41. Примеры расчета Моделирование процессов горения, тепло и
- 42. Примеры расчета Численный анализ пожаровзрывоопасности объектов нефтегазовой
- 43. Примеры расчета Моделирование течения многофазного потока в
- 44. http://www.ansys.com/products/academic/ansys-student Бесплатно лицензионную версию на 5 месяцев
Слайд 2Система уравнений Навье-Стокса
Уравнение неразрывности (сохранения массы)
Уравнение количества движения (сохранения импульса)
Слайд 3Система уравнений Навье-Стокса
Уравнение энергии (сохранения энергии)
Уравнение состояния
- давление;
-
- скорость;
- температура;
- время;
- полная энтальпия;
- статическая энтальпия;
‑ источниковый член для импульса;
- источниковый член для энергии;
- коэффициент динамической вязкости;
- коэффициент теплопроводности;
- оператор Гамильтона (набла);
- обозначает векторную величину
Слайд 4Анализ системы уравнений Навье-Стокса
дифференциальные уравнения в частных производных как первого, так
наличие нелинейной зависимости членов уравнений от переменных
Слайд 5за решение Математический институт Клэя назначил премию в 1 млн долларов
Необходимо доказать или опровергнуть существование глобального гладкого решения задачи Коши для трёхмерных уравнений Навье — Стокса.
Найти вектор скорости и давление, которые удовлетворяют системе уравнений Навье-Стокса и начальному условию
«Проблема тысячелетия»
Слайд 610 января 2014 года математик Мухтарбай Отелбаев опубликовал статью, в которой
6 февраля 2014 года Лауреатом Филдсовской медали Теренсом Тао была опубликована работа, доказывающая невозможность решения проблемы тысячелетия, посвященной задаче Навье-Стокса, существующими на настоящий момент средствами [2].
По состоянию на 2014 год подтверждённые решения этих уравнений найдены лишь в некоторых частных случаях.
В остальных случаях используется численное моделирование.
Решение уравнений
Слайд 7Пример точного решения
Течение Пуазейля
ламинарное течение жидкости через каналы в виде
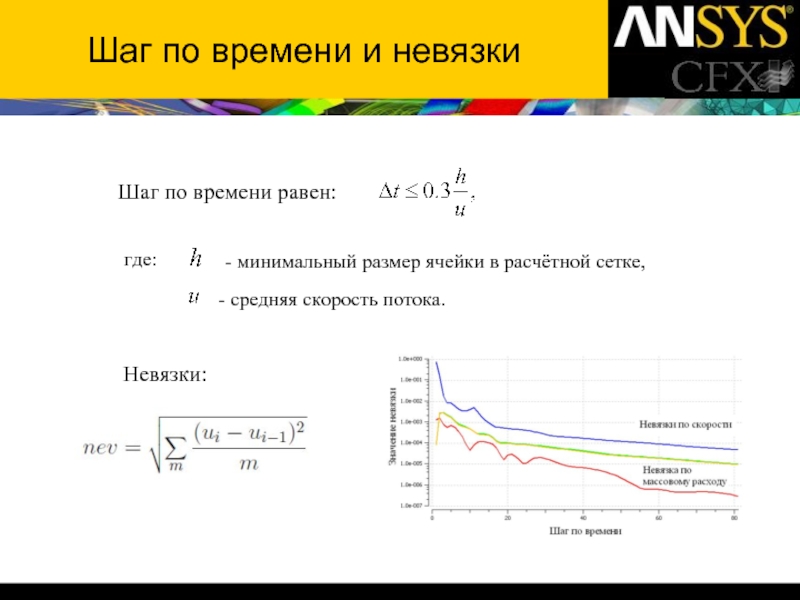
Слайд 8Структура численного решения
Дискретизация
метод конечных разностей (МКР)
метод конечных элементов (МКЭ)
метод конечных
Слайд 9Метод конечных объёмов
Уравнение неразрывности и количества движения в координатной форме
Интегрирование по
- контрольный объем
- контрольная поверхность, ограничивающая контрольный объем
- дифференциал декартовой составляющей вектора внешней нормали к поверхности
Слайд 10Дискретная форма интегральных соотношений
Метод конечных объёмов
- шаг по времени;
- вычисление для точки интегрирования и суммирование по всем точкам интегрирования данного контрольного объема
- величина соответствует предыдущему значению времени
- изменение массы через поверхность элемента
Слайд 11В МКО заложено точное интегральное сохранение таких величин, как масса, количество
Метод конечных элементов
Переменная
внутри объема
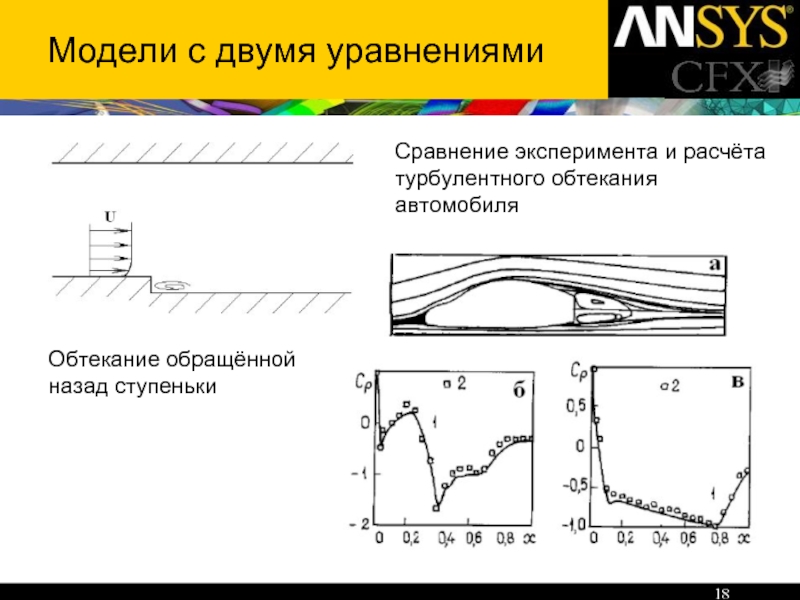
Слайд 12Шаг по времени и невязки
Шаг по времени равен:
где:
- минимальный размер ячейки
- средняя скорость потока.
Невязки:
Слайд 13Уравнения Рейнольдса
- напряжения Рейнольдса
Уравнения Навье-Стокса, осреднённые по Рейнольдсу
Слайд 14Модели турбулентности
Модели вихревой вязкости:
Однопараметрическая модель Колмогорова-Прандтля
Стандартная модель
Стандартная модель
Зонная модель
Зонная модель
Модель
Модели напряжений Рейнольдса:
Изотропная модель Launder-Reece-Rodi (LRR Reynolds Stress)
Квазиизотропная модель Launder-Reece-Rodi (QI Reynolds Stress)
Модель Speziale-Sarka-Gatski (SSG Reynolds Stress)
Модель SMC (Omega Reynolds Stress)
Модель BSL-RSS
Переходная модель ANSYS CFX Transition Model
Вихревые модели:
Модель крупных вихрей LES
Модель дискретных вихрей DES
Модель адаптивного масштаба SAS
Слайд 15 Алгебраические модели
Алгебраические модели - это простейший тип моделей турбулентности, согласно которым
Поскольку не решается никаких дополнительных уравнений движения, алгебраические модели также называют моделями нулевого порядка.
Тогда уравнение для напряжений Рейнольдса примет вид
Характерный масштаб пульсаций скорости записывается с помощью
характерного масштаба длины ?? (путь смешения Прандтля)
(1)
(2)
Слайд 16Турбулентная вязкость по физическому смыслу аналогична формуле вязкости для газов
где ?
? - плотность газа,
? - средняя скорость молекулы газа.
Алгебраические модели
Тогда уравнение для турбулентной вязкости примет вид
где ?? - это коэффициент пропорциональности, примем его =1.
Окончательно получаем формулу для напряжений Рейнольдса:
(3)
Слайд 17 Модели с одним уравнением
Кинетическая энергия единицы массы турбулентных флуктуаций
Уравнение для турбулентной
Чтобы замкнуть уравнение для кинетической энергии турбулентности, полага-
ется, что количество диссипированной турбулентной энергии определяется
энергосодержащим движением:
Слайд 18Обтекание обращённой назад ступеньки
Сравнение эксперимента и расчёта турбулентного обтекания автомобиля
Модели с
Слайд 19 Модели турбулентности
В общем виде, используемые в моделях с одним или двумя
дифференциальными
Расшифровка параметров для каждого вида уравнений:
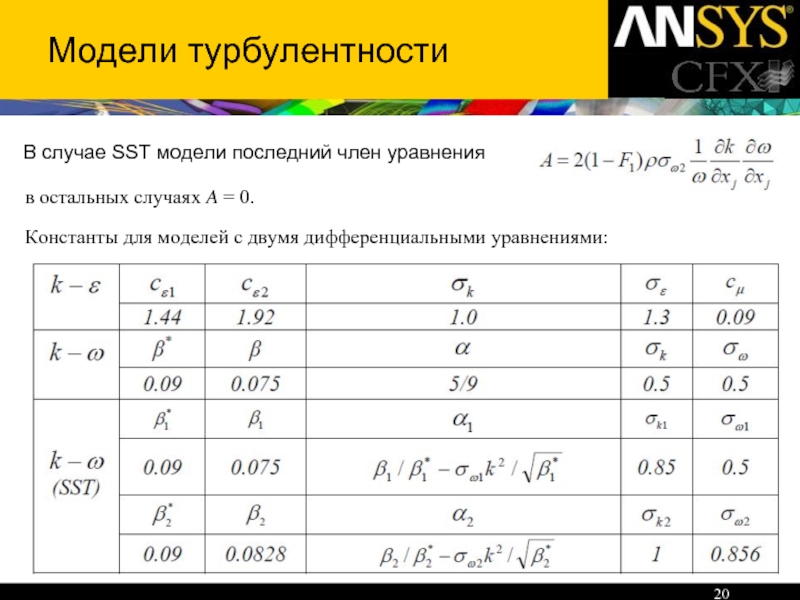
Слайд 20В случае SST модели последний член уравнения
Модели турбулентности
в остальных случаях A
Константы для моделей с двумя дифференциальными уравнениями:
Слайд 22Цикл проектирования и анализа
Создание геометрической модели (CAD)
Теоретический анализ, построение модели
Построение расчетной
Гидро-, газодинамический расчет и анализ (CFX)
Оптимизация
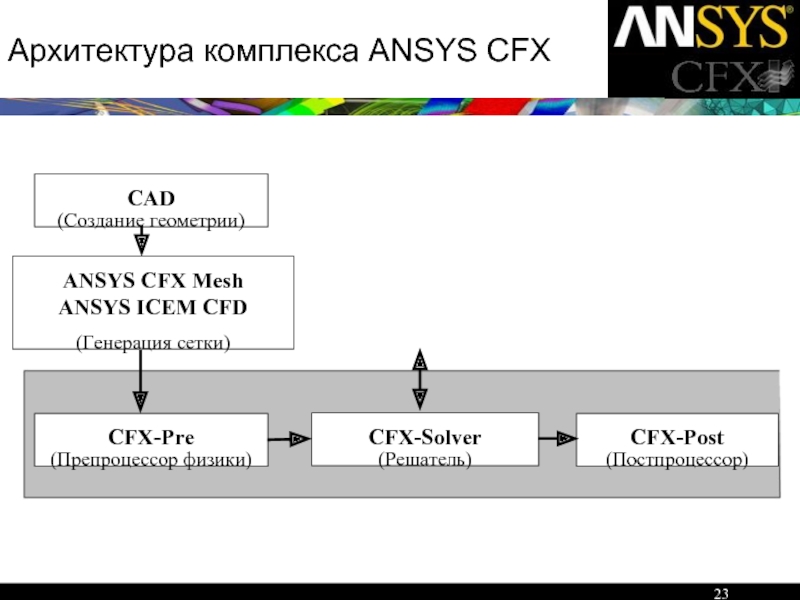
Слайд 23Архитектура комплекса ANSYS CFX
CFX-Pre
(Препроцессор физики)
CFX-Post
(Постпроцессор)
CFX-Solver
(Решатель)
ANSYS CFX Mesh
ANSYS ICEM CFD
(Генерация
CAD
(Создание геометрии)
Слайд 24CAD
Система автоматизации проектных работ (САПР) или CAD (англ. Computer-Aided Design) —
В современных системах проектирования CAD получает данные из систем твёрдотельного моделирования CAE (Computer-aided engineering), и передаёт в CAM (Computer-aided manufacturing) для подготовки производства (например генерации программ обработки деталей для станков с ЧПУ или ГАПС (Гибких Автоматизимрованных Производственных Систем)).
Слайд 25CAD
В ANSYS CFX могут импортироваться геометрические данные из CAD:
Solid Works (машиностроение);
Solid
Catia [V5] (аэрокосмическая промышленность);
BladeGen (лопаточные устройства турбомашин);
ACIS (3D CAD-система);
Parasolid и другие.
Слайд 26Комплекс ANSYS CFX
1. ANSYS CFX-Pre – приложение, в котором реализован процесс
2. ANSYS CFX-Solver – приложение, реализующее процесс решения задачи вычислительной гидродинамики.
3. ANSYS CFX-Post – это программа, предназначенная для анализа, визуализации и представления результатов, полученных в ходе решения задачи посредством ANSYS CFX Solver.
Слайд 27CFX Mesh
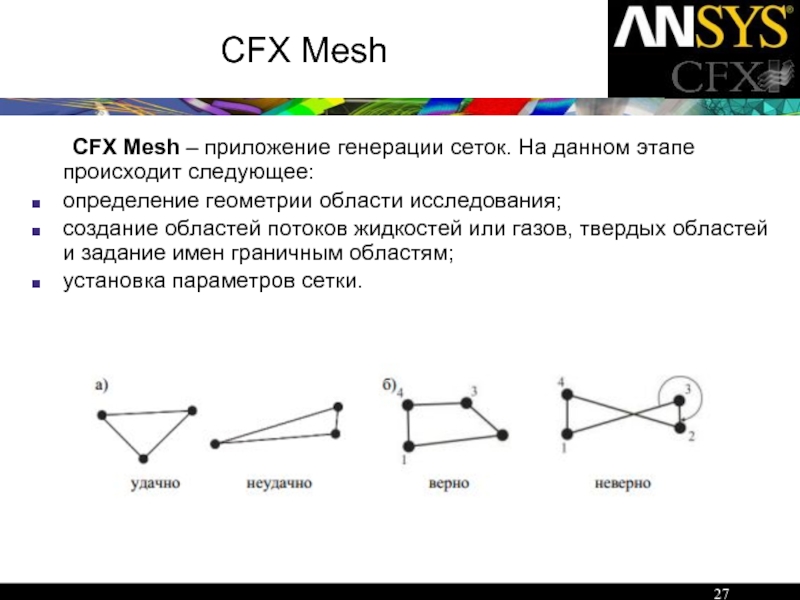
CFX Mesh – приложение генерации сеток. На данном этапе происходит
определение геометрии области исследования;
создание областей потоков жидкостей или газов, твердых областей и задание имен граничным областям;
установка параметров сетки.
Слайд 28ANSYS ICEM CFD
ANSYS ICEM CFD - Комплексное решение для задач генерации
ICEM CFD Tetra - полностью автоматический генератор неструктурированных объемных тетраэдрических сеток.
ICEM CFD HEXA - создание гексаэдрической сетки в полуавтоматическом режиме на основе любой геометрии.
Слайд 29ANSYS CFX-Pre
Физический препроцессор ANSYS CFX-Pre импортирует сетку, созданную генераторами сеток:
CFX Mesh;
ICEM
ANSYS;
ANSYS Meshing;
FLUENT;
Nastran
и другие.
Слайд 30ANSYS CFX-Pre
ANSYS CFX-Pre реализует процесс определения физики задачи:
физической модели;
её параметров и
граничные условия (входные, выходные);
модель теплообмена.
Слайд 31ANSYS CFX-Solver
Решатель ANSYS CFX - Solver импортирует задачу, поставленную посредством ANSYS
Слайд 32ANSYS CFX-Solver
ANSYS CFX - Solver реализует процесс решения задачи вычислительной гидро-
уравнения в частных производных интегрируются по всему объёму задачи в области исследования, соответствует применению закона сохранения (масс или момента) к каждой исследуемой области;
полученные интегральные уравнения преобразуются в систему алгебраических уравнений путем аппроксимирования членов в интегральных уравнениях;
алгебраические уравнения решаются численным методом.
Слайд 33ANSYS CFX-Post
Постпроцессор ANSYS CFX-Post предназначен для анализа, визуализации и представления результатов,
визуализация геометрии и исследуемых областей;
векторные графики для визуализации направления и величины потоков;
визуализация изменения скалярных величин (такие как температура, давление) внутри исследуемой области.
Слайд 34ANSYS Workbench
ANSYS Workbench входит в состав комплекса ANSYS и обеспечивает унифицированную
Слайд 35ANSYS Workbench
ANSYS Workbench включает следующие приложения:
DesignModeler;
CFX-Mesh;
Simulation;
FE Modeler;
DesignXplorer;
Engineering Data;
Customization and the Workbench
Слайд 37Области применения
Аэрокосмическая промышленность: процессы обтекания тел, химические процессы горения в ДВС,
Турбомашиностроение: потоки в турбинах, процессы вращения турбин
Нефтегазовая и химическая промышленность: химические процессы горения, процессы течения
Автомобилестроение: обтекание тел, процессы вентиляции, процессы горения в ДВС, процессы теплообмена
Судостроение и морская техника: процессы обтекания
Теплоэнергетика
Вентиляция и кондиционирование
Биомедицинские приложения: моделирование течения жидкостей организма; моделирование процессов теплообмена
Микроэлектромеханические системы MEMS: моделирование процессов теплообмена
Слайд 38Список источников
Ландау Л.Д., Лифшиц Е.М. Механика сплошных сред. М. 1953. 788
http://ru.wikipedia.org/wiki/%D3%F0%E0%E2%ED%E5%ED%E8%FF_%CD%E0%E2%FC%E5_%97_%D1%F2%EE%EA%F1%E0
Белов И. А., Исаев С. А. Моделирование турбулентных течений: Уч. пос. – СПб.: Балт. гос. техн. ун-т, 2001. – 108 с., ил.
Флетчер К. Вычислительные методы в динамике жидкостей: В 2-х томах: Т. 1: Пер. с англ. – М.: Мир, 1991. – 504 с, ил.
ANSYS CFX v.10. Release. Theory Reference.
Антипина Н.А. Математические модели рабочих процессов устройств для защиты нефтяного насоса от засорения // Диссертация на соискание ученой степени кандидата технических наук, Пермь, 2012
Слайд 39Примеры расчета
Аппарат со встречно-закрученными потоками
Общий вид расчетной области.
Картина течения в осевом
Слайд 41Примеры расчета
Моделирование процессов горения, тепло и массообмена в топках котлов на
Общая структура течения в топочной камере и распределение температуры в топке 120 МВт котла
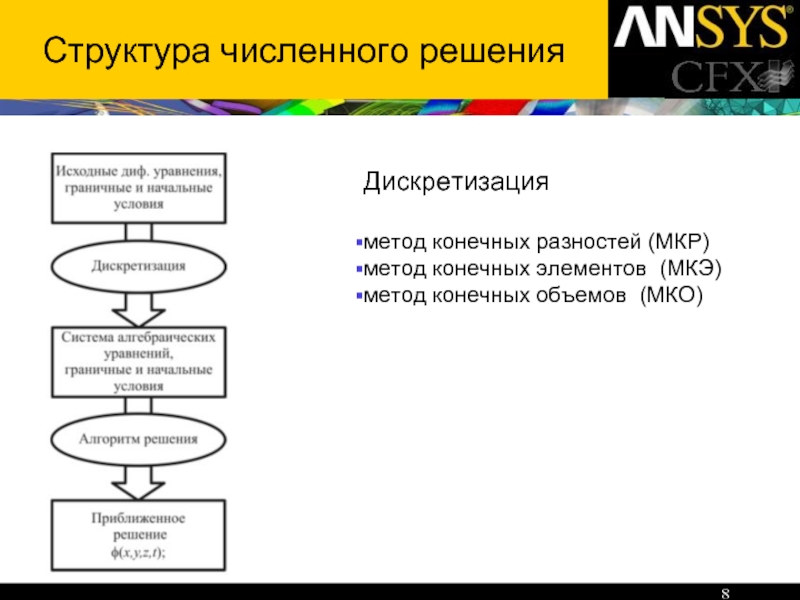
Слайд 42Примеры расчета
Численный анализ пожаровзрывоопасности объектов нефтегазовой отрасли, промышленности и строительства
Моделирование утечки
Изоповерхность концентрации углерода в момент времени t = 120 сек (CFX-Post)
Слайд 43Примеры расчета
Моделирование течения многофазного потока в трубопроводе с ловушкой для конденсата
Пример
На фотографии ловушки для конденсата
Внешний вид расчетной сетки до адаптации
Слайд 44http://www.ansys.com/products/academic/ansys-student
Бесплатно лицензионную версию на 5 месяцев можно скачать здесь:
Как решать задачи
Лыкова
crym@yandex.ru
8-908-26-000-27


















![CAD В ANSYS CFX могут импортироваться геометрические данные из CAD:Solid Works (машиностроение);Solid Edge (2D/3D CAD-система);Catia [V5]](/img/tmb/3/220015/58659bf300a222b2138d3e08b6190378-800x.jpg)