- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Теория и свойства меркаторской проекции презентация
Содержание
- 1. Теория и свойства меркаторской проекции
- 2. 1. Требования, предъявляемые к морским навигационным картам
- 3. Удовлетворяющие этим требованиям карты построены по проекции,
- 4. 2. Математическое обоснование принципа меркаторской проекции Представим,
- 5. Теперь разрежем цилиндр по образующей (по одному
- 6. Для доказательства этого положения рассмотрим, где обозначим
- 7. 3. Меридиональные части Расстояния по меридиану от
- 8. Расстояние по меридиану на меркаторской проекции между
- 9. Поэтому при измерении по морской навигационной карте
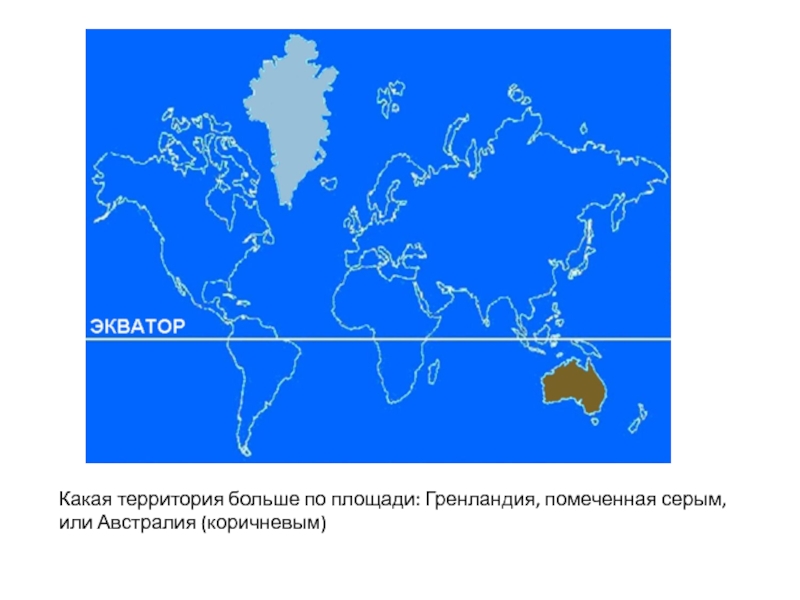
- 10. Какая территория больше по площади: Гренландия, помеченная серым, или Австралия (коричневым)
- 11. Площадь Австралии составляет 7,7 млн км2, а
- 12. Мореплаватели XIII–XVI века пользовались портуланами — картами,
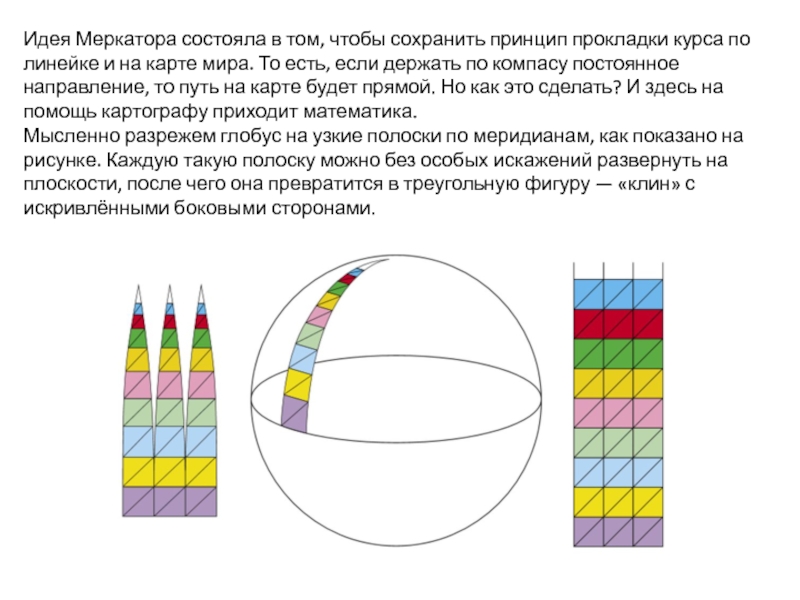
- 13. Идея Меркатора состояла в том, чтобы сохранить
- 14. Однако глобус при этом оказывается рассечённым, а
- 15. Выполним завершающие действия. Выпрямим «почти квадраты» до
- 16. В 1571 году Меркатор завершил свою главную
Слайд 21. Требования, предъявляемые к морским навигационным картам
При выборе проекции для построения
*линия пути судна, идущего постоянным курсом, т. е. локсодромия, изображалась прямой линией;
*величина углов, измеряемых с судна между разными ориентирами на местности, соответствовала величинам углов между теми же ориентирами на карте, т. е. проекция карты должна быть равноугольной;
*масштаб в пределах карты изменялся в возможно малых пределах т. е. искажения длин на карте не превышали ошибок графических построений и измерений на карте, выполняемых с помощью прокладочного инструмента.
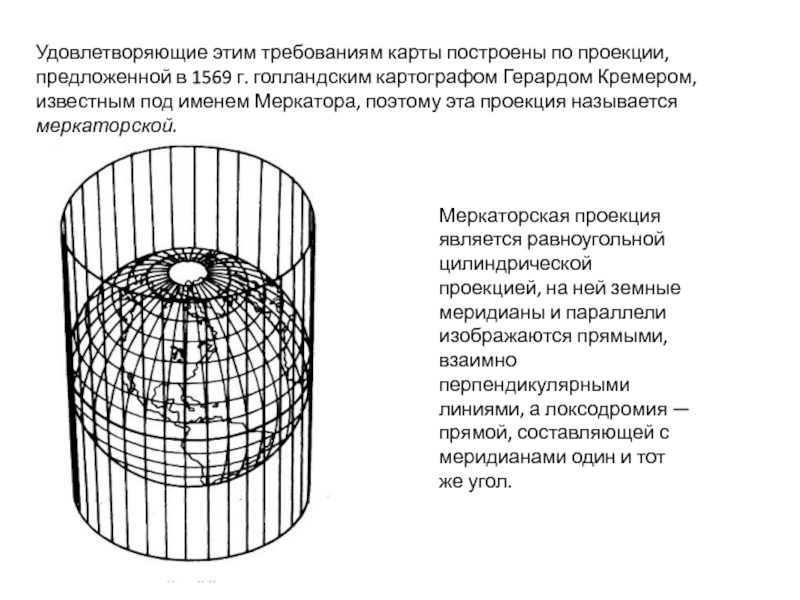
Слайд 3Удовлетворяющие этим требованиям карты построены по проекции, предложенной в 1569 г.
Меркаторская проекция является равноугольной цилиндрической проекцией, на ней земные меридианы и параллели изображаются прямыми, взаимно перпендикулярными линиями, а локсодромия — прямой, составляющей с меридианами один и тот же угол.
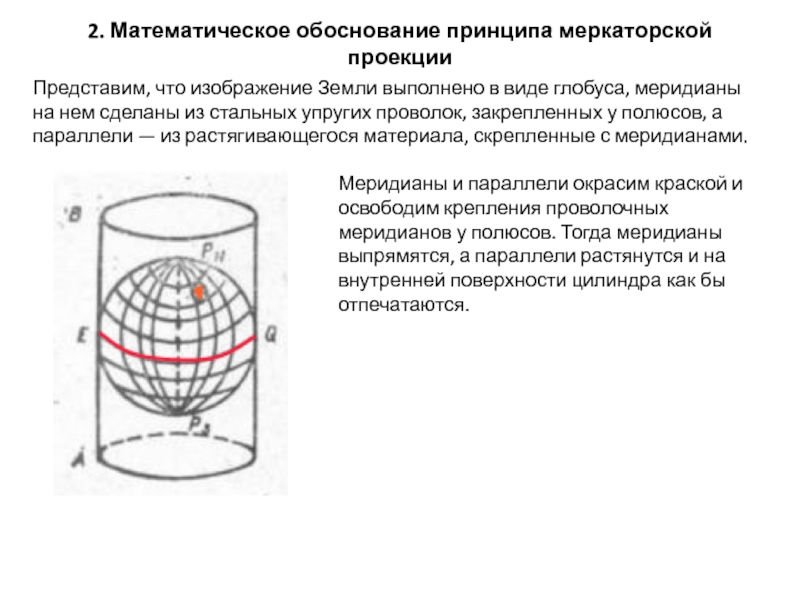
Слайд 42. Математическое обоснование принципа меркаторской проекции
Представим, что изображение Земли выполнено в
Меридианы и параллели окрасим краской и освободим крепления проволочных меридианов у полюсов. Тогда меридианы выпрямятся, а параллели растянутся и на внутренней поверхности цилиндра как бы отпечатаются.
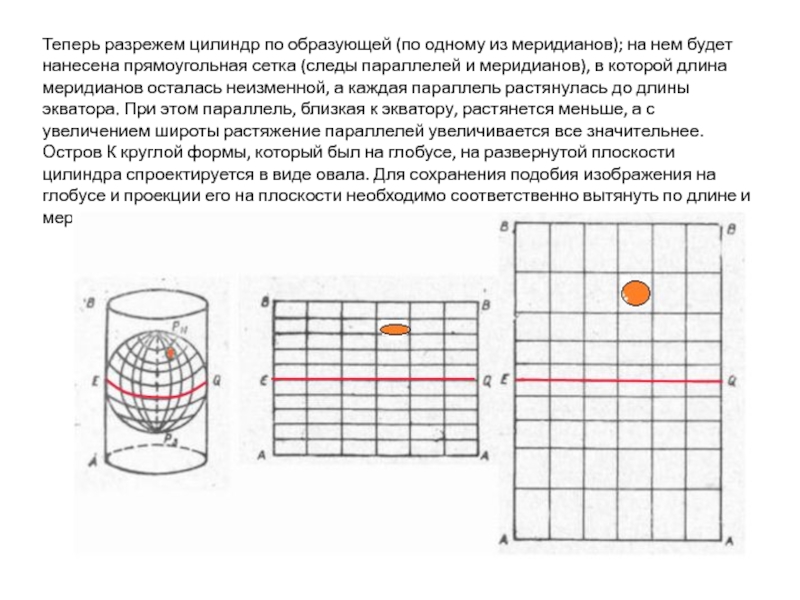
Слайд 5Теперь разрежем цилиндр по образующей (по одному из меридианов); на нем
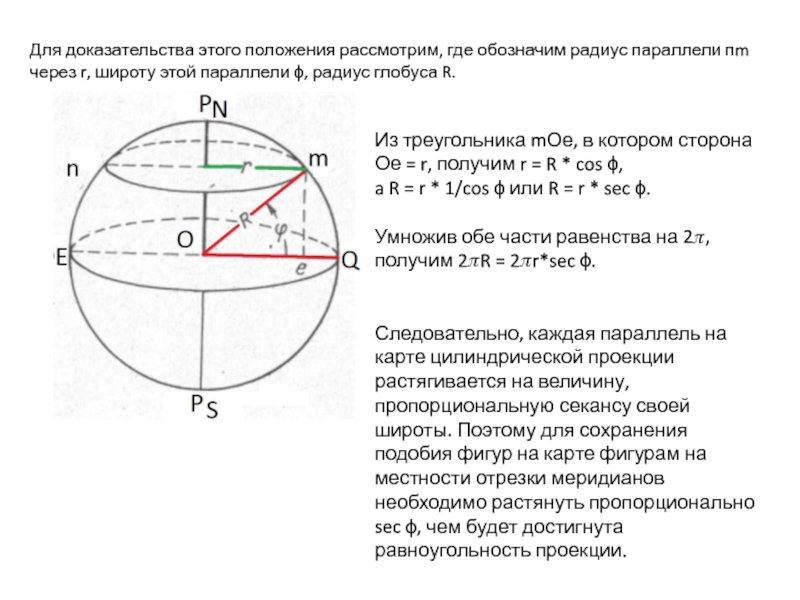
Слайд 6Для доказательства этого положения рассмотрим, где обозначим радиус параллели пm через
Из треугольника mОе, в котором сторона
Ое = r, получим r = R * cos ϕ,
a R = r * 1/cos ϕ или R = r * sec ϕ.
Умножив обе части равенства на 2?, получим 2?R = 2?r*sec ϕ.
Следовательно, каждая параллель на карте цилиндрической проекции растягивается на величину, пропорциональную секансу своей широты. Поэтому для сохранения подобия фигур на карте фигурам на местности отрезки меридианов необходимо растянуть пропорционально sec ϕ, чем будет достигнута равноугольность проекции.
Слайд 73. Меридиональные части
Расстояния по меридиану от экватора до данных параллелей на
Они обозначаются буквой D.
Для удобства меридиональные части выражают длиной дуги экватора, называемой экваториальной милей.
В табл. 2.28а (МТ—2000) длина меридиональных частей рассчитана применительно к эллипсоиду Красовского.
Значения в таблице вычислены для широт от 0 до 89° 59' через 1' широты с точностью до 0,1 экваториальной мили.
Для определения величины меридиональных частей на промежуточных значениях минуты широты (для десятых долей 1') применяют простое интерполирование.
Слайд 8Расстояние по меридиану на меркаторской проекции между двумя параллелями, выраженное в
Разность меридиональных частей двух параллелей равна алгебраической разности меридиональных частей этих параллелей
AD=D2-D1
Меридиональные части используют при построении картографической сетки морских карт в меркаторской проекции, а разность меридиональных частей входит в одну из основных формул письменного счисления
Разность меридиональных частей двух параллелей, отстоящих друг от друга на 1', даст нам длину отрезка, изображающего на карте меркаторской проекции одну экваториальную минуту в данной широте.
Эта разность меридиональных частей представляет не что иное, как изображение одной морской мили на карте меркаторской проекции. Меркаторской милей пользуются как единицей линейного масштаба для измерения широт и расстояний на карте меркаторской проекции.
Поскольку морская миля, как это было указано ранее, имеет постоянную величину на поверхности Земли, то она на морской карте меркаторской проекции изображается отрезками различной длины, в зависимости от широты места, к которому она относится.
Слайд 9Поэтому при измерении по морской навигационной карте расстояний между какими-либо точками
Практически для измерения расстояний на карте меркаторской проекции пользуются длиной меркаторской мили, соответствующей средней широте измеряемой линии.
Если принимать Землю за шар, то МЧ вычисляется по формуле
Для сфероида надо учесть сжатие Земли и формула для МЧ примет вид:
Где - эксцентриситет эллипсоида вращения;
а, в - большая и малая полуоси земного эллипсоида.
Слайд 10Какая территория больше по площади: Гренландия, помеченная серым, или Австралия (коричневым)
Слайд 11Площадь Австралии составляет 7,7 млн км2, а площадь Гренландии — только
Слайд 12Мореплаватели XIII–XVI века пользовались портуланами — картами, на которых изображался бассейн
Слайд 13Идея Меркатора состояла в том, чтобы сохранить принцип прокладки курса по
Мысленно разрежем глобус на узкие полоски по меридианам, как показано на рисунке. Каждую такую полоску можно без особых искажений развернуть на плоскости, после чего она превратится в треугольную фигуру — «клин» с искривлёнными боковыми сторонами.
Слайд 14Однако глобус при этом оказывается рассечённым, а карта должна быть сплошной,
Слайд 15Выполним завершающие действия. Выпрямим «почти квадраты» до настоящей квадратной формы. Как
Однако углы между направлениями при таком построении останутся неискажёнными, потому что каждый квадрат практически только изменился в масштабе, а направления при простом увеличении картинки не меняются. И именно этого добивался Меркатор, когда он придумывал свою проекцию!
Капитан может прокладывать свой курс на карте по линейке и вести по этому курсу свой корабль. При этом корабль будет плыть по линии, идущей под одним и тем же углом ко всем меридианам. Эта линия называется локсодромией.
Плавание по локсодромии очень удобно, поскольку оно не требует никаких специальных расчётов. Правда, локсодромия не является кратчайшей линией между двумя пунктами на земной поверхности.
Такую кратчайшую линию можно определить, натянув на глобусе нитку между этими пунктами.
Слайд 16В 1571 году Меркатор завершил свою главную работу — всеобъемлющий труд
Меркатор вспомнил миф об Атланте, или Атласе, который держит на своих плечах небесный свод.
Сборник карт всей земной поверхности, как бы держащей на себе небеса, он и назвал атласом.
С тех пор слово «атлас» стало обычным для собрания карт.