- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Реология горных пород презентация
Содержание
- 1. Реология горных пород
- 2. Виды деформаций Упругая Пластическая Вязкая
- 3. Упругость Способность тела восстанавливать свою форму и
- 4. Пластичность Пластичность - свойство горной породы необратимо
- 5. Механизмы пластической деформации Пластическая деформация обеспечивается: -
- 6. Вязкость Свойство тела оказывать сопротивле-ние перемещению молекул относи-тельно друг друга.
- 7. Идеальные реологические тела - носители идеальных деформаций
- 8. Аксиомы реологии Первая аксиома: под действием равномерного
- 9. Возвращение в исходному вопросу: С помощью какого
- 10. Вторая аксиома Каждый реальный материал обладает всеми
- 11. Третья аксиома Существует иерархия
- 12. ПРАВИЛА ПОСТРОЕНИЯ СЛОЖНЫХ ТЕЛ τ = τ1 = ... =
- 13. СЛОЖНЫЕ РЕОЛОГИЧЕСКИЕ ТЕЛА 2. Тело Максвелла: М
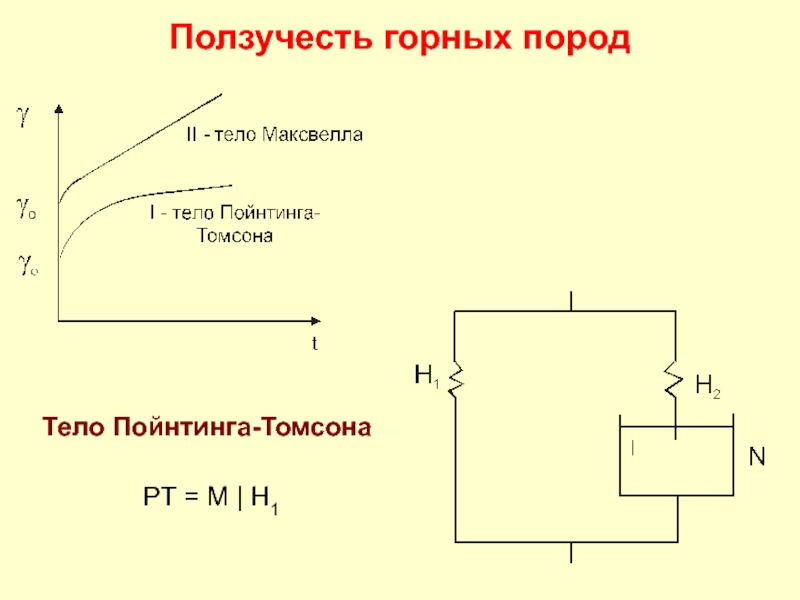
- 14. Ползучесть горных пород Тело Пойнтинга-Томсона PT = M | H1
- 15. Кривые изменения сдвиговой деформации во времени
- 16. Ползучесть и пластическая деформация По внешним признакам
- 17. К чему приводит ползучесть горных пород стенки
- 18. Ползучесть горных пород стенки скважины Инициатор ползучести
- 19. Ползучесть горных пород стенки скважины В мерзлых
- 20. Ползучесть Склонны к ползучести соленосные породы, многолетние
- 21. Релаксация напряжений Возвращаемся к исходному уравнению б)
- 22. Релаксация напряжений Релаксация напряжений характеризуется периодом (временем)
- 23. Тело Максвелла Тело Максвелла – упруго-вязкое тело.
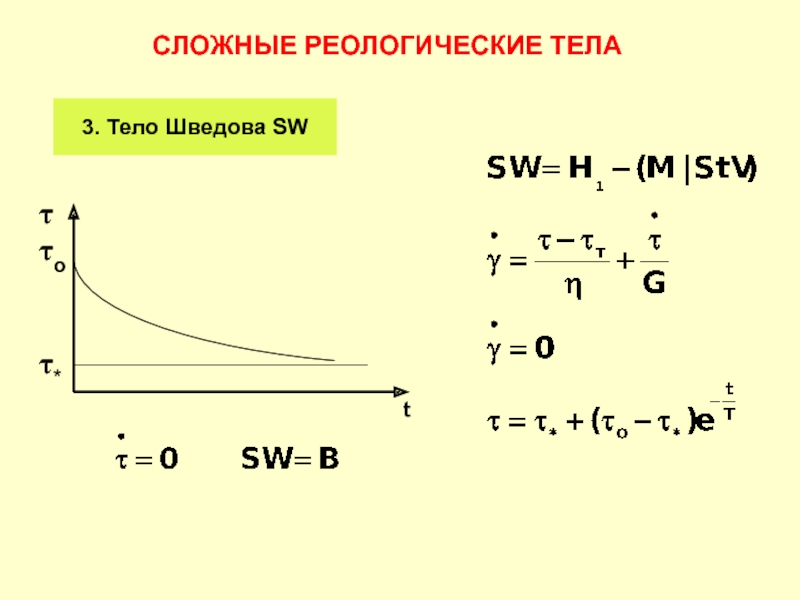
- 24. 3. Тело Шведова SW СЛОЖНЫЕ РЕОЛОГИЧЕСКИЕ ТЕЛА
- 25. Физические уравнения Упругий массив горных пород εx
- 26. Физические уравнения в) Вязкий массив горных пород теория старения теория упрочнения
- 27. Примерные вопросы к рейтингу Тело Максвелла, время
Слайд 1Реология горных пород
С помощью какого механического воздействия можно распознать природу тел
Слайд 3Упругость
Способность тела восстанавливать свою форму и объем (у твердых тел) или
только объем (жидкость, газы) после прекращения действия сил.
Упругая деформация исчезает после снятия нагрузки.
Слайд 4Пластичность
Пластичность - свойство горной породы необратимо изменять свою форму под действием
Уравнение состояния можно записать так:
Слайд 5Механизмы пластической деформации
Пластическая деформация обеспечивается:
- межзерновым скольжением;
- трансляцией;
- перекристаллизацией.
Межзерновое скольжение -
Трансляция – скольжение одного слоя кристал-лической решетки минерала относительно другого.
Перекристаллизация - искажение и изменение кристаллической решетки.
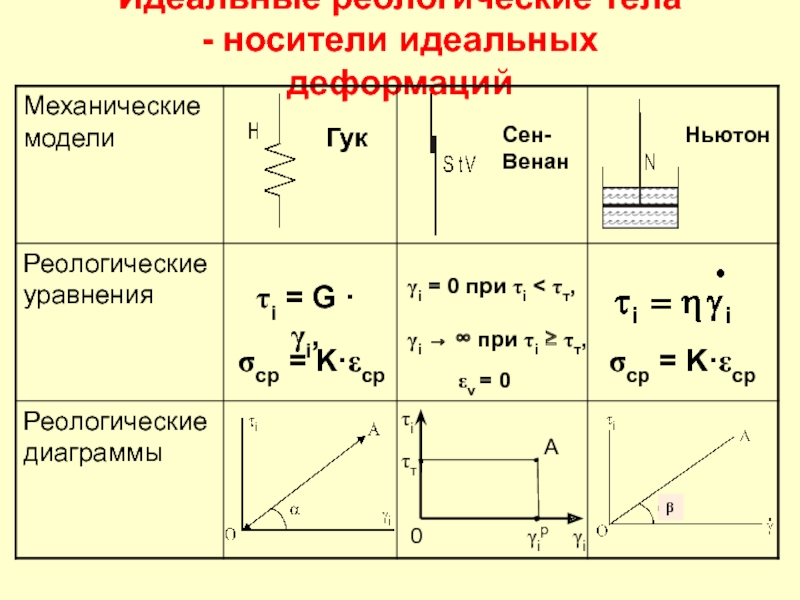
Слайд 7Идеальные реологические тела
- носители идеальных деформаций
Гук
Сен-Венан
Ньютон
τi = G · γi,
σср =
γi = 0 при τi < τт,
γi → ∞ при τi ≥ τт,
εv = 0
σср = K·εср
Слайд 8Аксиомы реологии
Первая аксиома: под действием равномерного всестороннего давления все материалы ведут
Слайд 9Возвращение в исходному вопросу:
С помощью какого механического воздействия можно распознать природу
ОТВЕТ:
Слайд 10Вторая аксиома
Каждый реальный материал обладает всеми реологическими свойствами, хотя и в
H, StV, N
H, StV, N
H, StV, N
Слайд 11
Третья аксиома
Существует иерархия реологичес-ких тел: тело, низшее по иерархии, должно
Последовательное и параллельное соединение идеальных тел: моделирование реальных тел.
Слайд 12ПРАВИЛА ПОСТРОЕНИЯ СЛОЖНЫХ ТЕЛ
τ = τ1 = ... = τn,
γ = γ1 + ... + γn
τ =
γ = γ1 = ... = γn
1. Последовательное соединение элементов
2. Параллельное соединение элементов
СЛОЖНЫЕ РЕОЛОГИЧЕСКИЕ ТЕЛА
1. Тело Прандтля: P = H – StV
γs – γe = γp
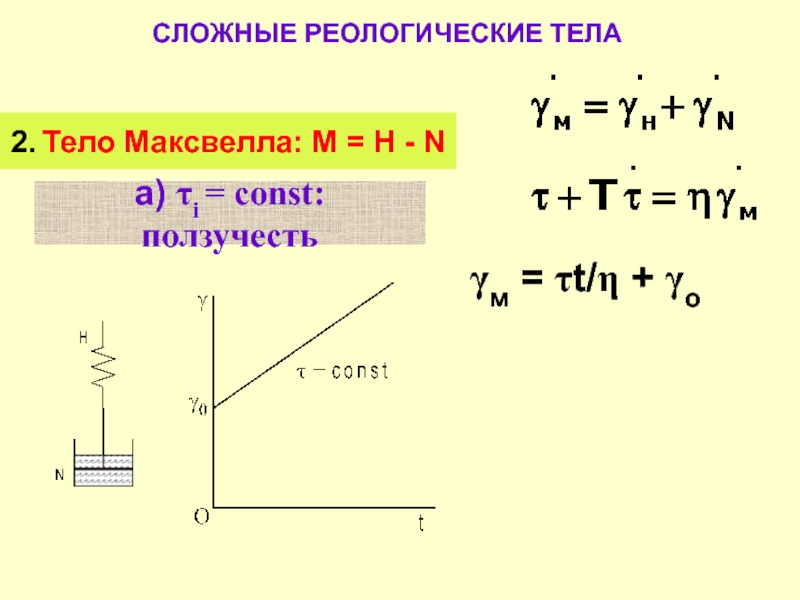
Слайд 13СЛОЖНЫЕ РЕОЛОГИЧЕСКИЕ ТЕЛА
2. Тело Максвелла: М = Н - N
а) τi
γм = τt/η + γо
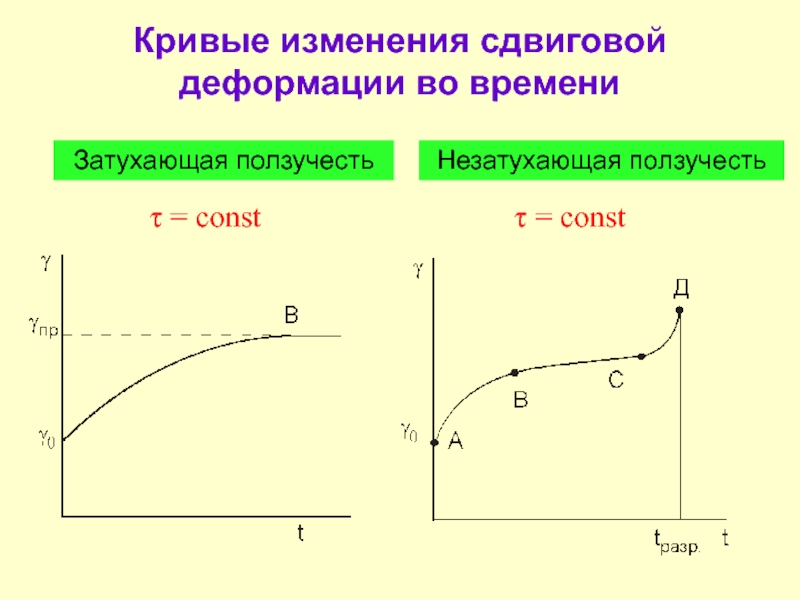
Слайд 15Кривые изменения сдвиговой деформации во времени
Затухающая ползучесть
Незатухающая ползучесть
τ =
τ = const
Слайд 16Ползучесть и пластическая деформация
По внешним признакам ползучесть похожа на пластическое течение
Ползучесть может возникнуть при нагрузках, меньших предела упругости (текучести) горных пород, причем длительность воздей-ствия нагрузки для фиксирования ползучести, как правило, велика.
Слайд 17К чему приводит ползучесть горных пород стенки скважины
Потеря устойчивости пород в
Слайд 18Ползучесть горных пород стенки скважины
Инициатор ползучести у горных пород разный:
- Ползучесть песчаников и других осадочных пород, имеющих глинистый цемент, объясняется свойства-ми этого цемента.
Слайд 19Ползучесть горных пород стенки скважины
В мерзлых горных породах роль цементиру-ющего вещества
Ползучесть соленосных пород определяется наличием в них солей. Эти горные породы начинают течь при весьма малых нагрузках, так как соли не имеют несущей способности и передают нагрузку так же, как жидкости.
Слайд 20Ползучесть
Склонны к ползучести соленосные породы, многолетние мерзлые пласты горных пород, аргиллиты,
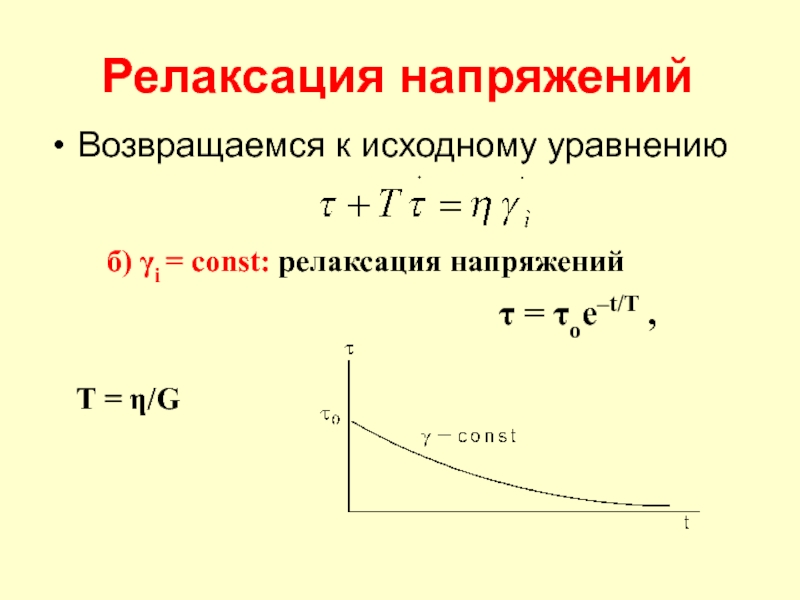
Слайд 21Релаксация напряжений
Возвращаемся к исходному уравнению
б) γi = const: релаксация напряжений
τ =
T = η/G
Слайд 22Релаксация напряжений
Релаксация напряжений характеризуется периодом (временем) релаксации (время, в течение которого
Время релаксации:
Известняки – 1,05 · 105 – 1010 с;
Песчаники – (1,07 - 2,6) · 105 с;
Глинистые сланцы (2,6 – 34,5) · 105 с;
Плотные глины – (8,6 – 17,3) · 105 с.
Лед – 102 -103 c;
Вода – 10– 11 с.
Слайд 23Тело Максвелла
Тело Максвелла – упруго-вязкое тело. Его поведение при деформировании оп-ределяется
- при t >> T – тело М ведет себя как жид-кость,
- при t << T – тело М ведет себя как твер-дое тело
Слайд 25Физические уравнения
Упругий массив горных пород
εx = [σx – v (σy +
εy = [σy – v (σx + σz)]/Е
εz = [σy – v (σx + σz)]/Е
γxy = τxy/G, γxz = τxz/G, γyz = τyz
б) Пластический массив горных пород
εx – εср = [(σх – σср)/2G] ∙ ω
εy – εср = [(σy – σср)/2G] ∙ ω
εz – εср = [(σz – σср)/2G] ∙ ω
γxy = τxy ∙ ω/G, γxz = τxz∙ ω/G, γyz = τyz ∙ ω/G
Слайд 27Примерные вопросы к рейтингу
Тело Максвелла, время релаксации и проявление упругих и
Дать определение понятию «ползучесть». Затухающая и незатухающая ползучесть. Кривые ползучести горных пород. Где при бурении ствола скважины возникают условия появления ползучести. К чему это приводит?
Охарактеризовать тело Прандтля. Привести деформационную кривую, характерную для этого тела?
Аксиомы реологии.
Написать реологические уравнения состояния, характеризующее изменение объема и формы тела Ньютона. Привести соответствующие графики.
Тела Гука, Сен-Венана, Ньютона.
Реологические параметры и их размерности.


















![Физические уравненияУпругий массив горных породεx = [σx – v (σy + σz)]/Еεy = [σy –](/img/tmb/4/323110/c5e8ca3b67cc1fbf2cb1cb317e362dbd-800x.jpg)







