Настенные знаки и пункты опорной сети, на которых невозможна установка прибора
Задача Ганзена
Линейная засечка
Полярный метод
Метод треугольника
Передача координат с вершины знака на землю
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Привязка геодезических построений к настенным знакам и пункту опорной сети, на котором невозможна установка прибора презентация
Содержание
- 1. Привязка геодезических построений к настенным знакам и пункту опорной сети, на котором невозможна установка прибора
- 2. 1. Настенные знаки и пункты опорной сети,
- 3. Рисунок 2 – Геодезический триангуляционный пункт по
- 4. Нормативные документы, регламентирующие способы закладки геодезических пунктов
- 5. 2. Задача Ганзена Рисунок 3 – Схема
- 6. Порядок решения: 1. Для определения вспомогательных углов
- 7. 3. Решением обратной геодезической задачи по исходным
- 8. 4. Вычисляют дирекционные углы направлений с исходных
- 9. 6. Из треугольников АВР и АВQ, используя
- 10. Контролем правильности измерений и вычислений является сравнение
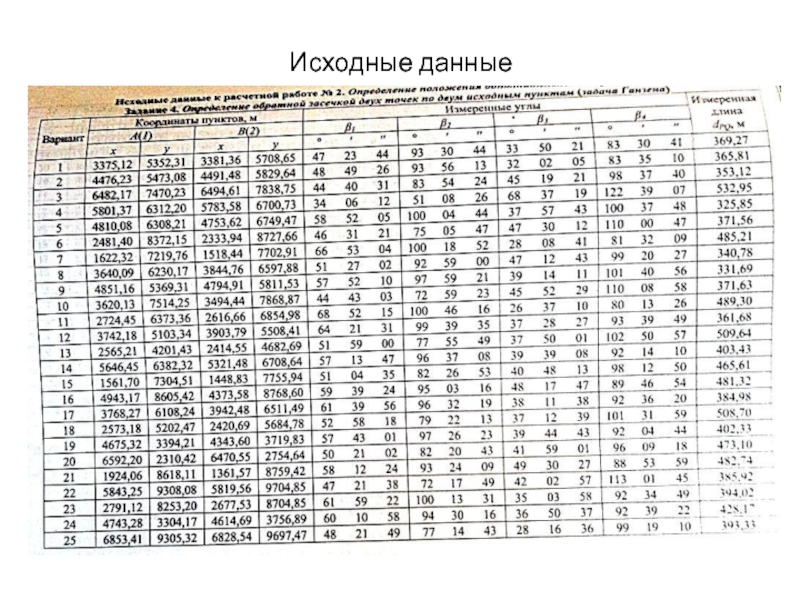
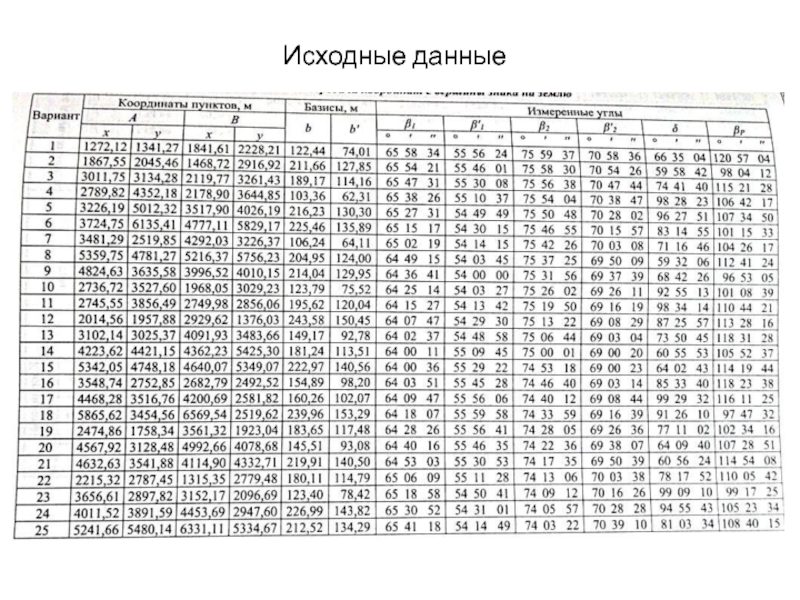
- 11. Исходные данные
- 12. 3. Линейная засечка Сущность линейной засечки состоит
- 13. При решении задачи по длинам сторон треугольников
- 14. Если в треугольнике известны все стороны, то
- 15. На практике решение задачи удобно выполнять по
- 16. Исходные данные
- 17. 4. Полярный метод Данный метод применяется при
- 18. Рисунок 5 – Схема снесения координат пункта
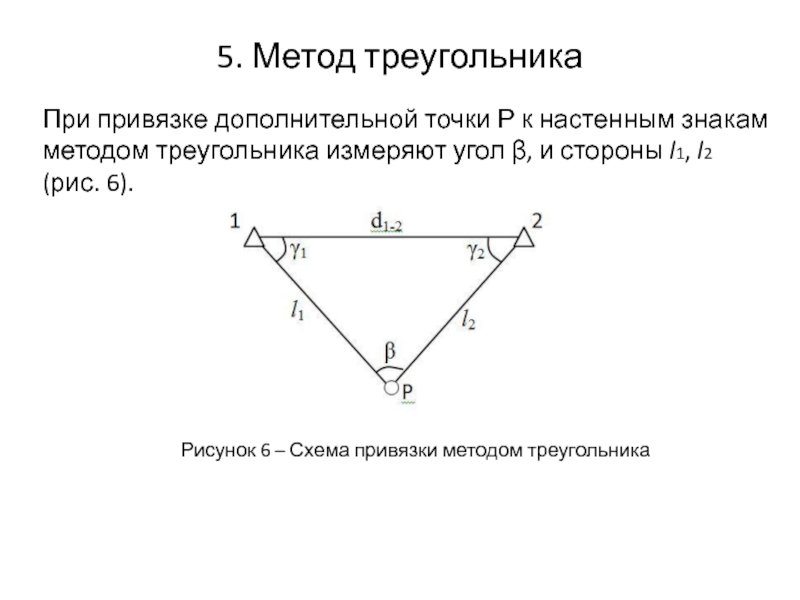
- 19. 5. Метод треугольника При привязке дополнительной точки
- 20. Вычисление координат т.Р выполняют в следующей последовательности:
- 21. 2. Находят дирекционные углы сторон 1-2, 1-А,
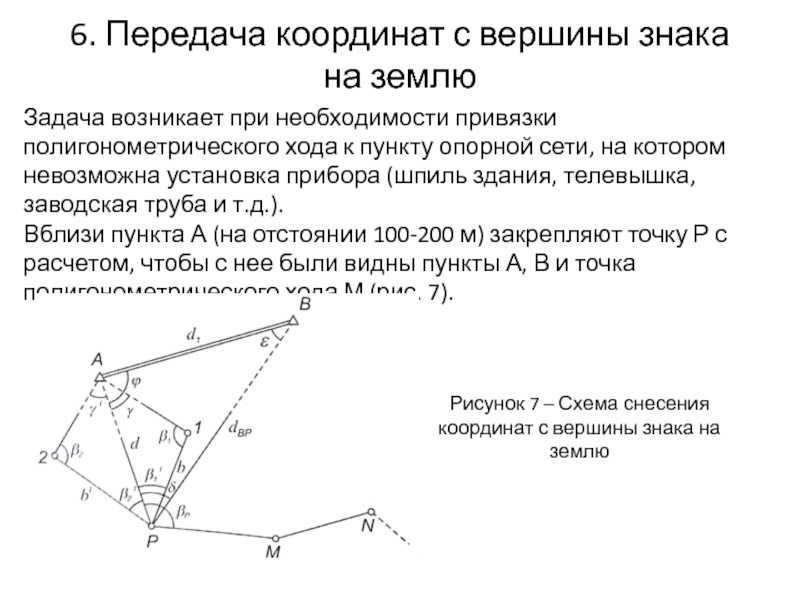
- 22. 6. Передача координат с вершины знака на
- 23. Из точки Р разбивают два базиса для
- 24. Задача решается в следующей последовательности: По известным
- 25. 3. Вычисляют дирекционный угол линии АР. Для
- 26. Контроль измерений и вычислений выполняют одним из
- 27. Оценка точности определения положения точки Р. Абсолютную
- 28. Исходные данные
Слайд 1Привязка геодезических построений к настенным знакам и пункту опорной сети, на
Слайд 21. Настенные знаки и пункты опорной сети, на которых невозможна установка
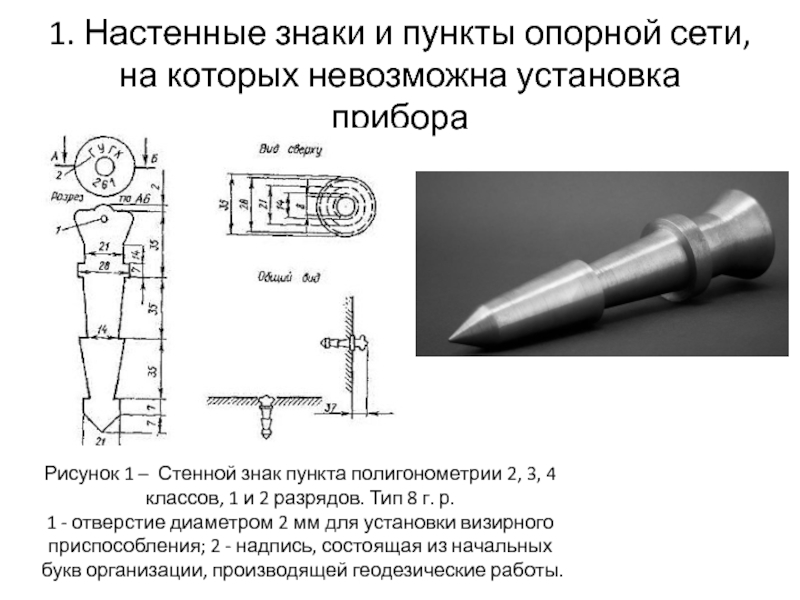
Рисунок 1 – Стенной знак пункта полигонометрии 2, 3, 4 классов, 1 и 2 разрядов. Тип 8 г. р.
1 - отверстие диаметром 2 мм для установки визирного приспособления; 2 - надпись, состоящая из начальных букв организации, производящей геодезические работы.
Слайд 3Рисунок 2 – Геодезический триангуляционный пункт по ул. Высоцкого на крыше
Слайд 4Нормативные документы, регламентирующие способы закладки геодезических пунктов и их конструкции:
Правила закладки
Инструкция по топографической съемке в масштабах 1:5000, 1:2000, 1:1000 и 1:500 (ГКИНП-02-033-82)
Основные положения о государственной геодезической сети российской федерации (ГКИНП (ГНТА)-01-006-03) 4. Руководство по созданию и реконструкции городских геодезических сетей с использованием спутниковых систем ГЛОНАСС/GPS (ГКИНП (ОНТА)-01-271-03)
и др.
Слайд 52. Задача Ганзена
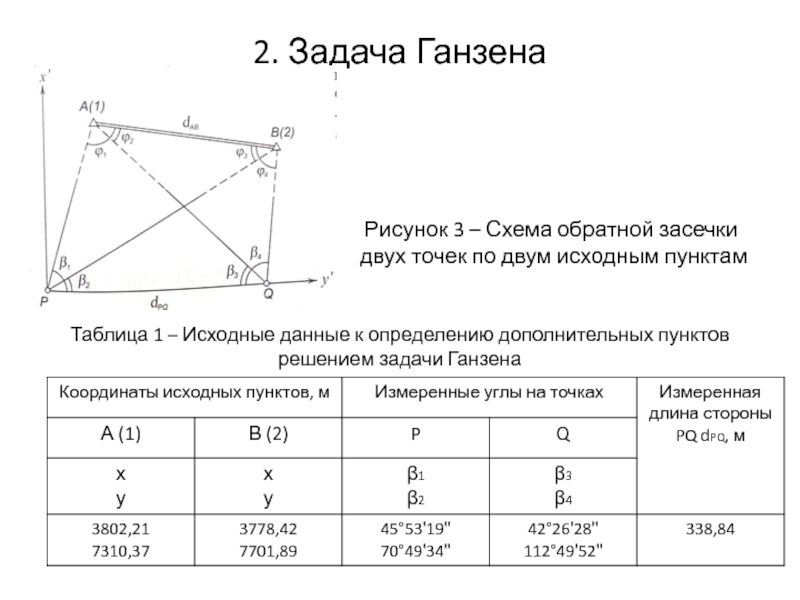
Рисунок 3 – Схема обратной засечки двух точек по
Таблица 1 – Исходные данные к определению дополнительных пунктов решением задачи Ганзена
Слайд 6Порядок решения:
1. Для определения вспомогательных углов ϕ1, ϕ2, ϕ3, и ϕ4
хʹР = 0; уʹР = 0; хʹQ = 0; уʹQ = 1000,00м.
2. Из треугольников PAQ и PBQ по формулам Юнга находят условные координаты точек А (хʹ1, уʹ1) и В (хʹ2, уʹ2):
Слайд 73. Решением обратной геодезической задачи по исходным координатам пунктов А и
Слайд 84. Вычисляют дирекционные углы направлений с исходных пунктов на определяемые точки,
αʹАР = αʹPQ +180° - β2 = 90° + 180° - 70°49ʹ34ʹʹ = 199°10ʹ26ʹʹ;
αʹАQ = αʹPQ + β3 = 90° + 42°26ʹ28ʹʹ = 132°26ʹ28ʹʹ;
αʹBР = αʹPQ +180° - (β2 - β1)= 90° + 180° - (70°49ʹ34ʹʹ - 45°53ʹ19ʹʹ) = 245°03ʹ45ʹʹ;
αʹBQ = αʹPQ + β4 = 90° + 112°49ʹ52ʹʹ = 202°49ʹ52ʹʹ.
5. Используя полученные условные дир. углы, вычисляют вспомогательные углы ϕ1, ϕ2, ϕ3, и ϕ4.
ϕ1 = αʹАР - αʹАB = 199°10ʹ26ʹʹ - 96°35ʹ01ʹʹ = 102°35ʹ25ʹʹ;
ϕ2 = αʹАQ - αʹАB = 132°26ʹ28ʹʹ - 96°35ʹ01ʹʹ = 35°51ʹ27ʹʹ;
ϕ3 = αʹBA - αʹBP = 276°35ʹ01ʹʹ - 245°03ʹ45ʹʹ = 31°31ʹ16ʹʹ;
ϕ4 = αʹBA - αʹBQ = 276°35ʹ01ʹʹ - 202°49ʹ52ʹʹ = 73°45ʹ09ʹʹ.
Слайд 96. Из треугольников АВР и АВQ, используя вспомогательные углы ϕ1, ϕ2,
ΔАВР:
ΔАВQ:
Слайд 10Контролем правильности измерений и вычислений является сравнение длины стороны РQ, вычисленной
Расхождение |dPQ изм – dPQ расч| не должно превышать допусков, установленных инструктивными документами для соответствующего вида геодезических работ.
В рассмотренном примере расчетное значение длины PQ равно 388,82 м.
Тогда |dPQ изм – dPQ расч| ≈(1/19000)d, что не превышает допустимой относительной погрешности измерения длин сторон полигонометрии 1-го разряда (1:10000).
Слайд 123. Линейная засечка
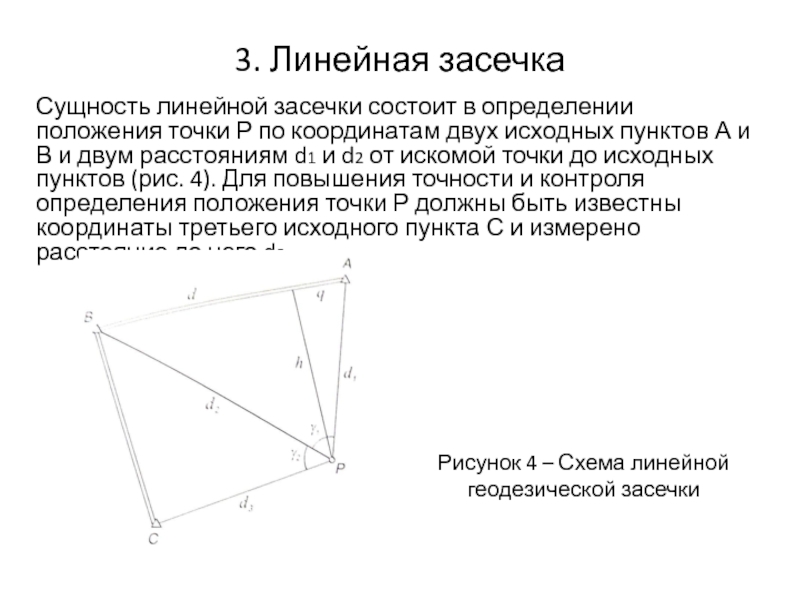
Сущность линейной засечки состоит в определении положения точки Р
Рисунок 4 – Схема линейной геодезической засечки
Слайд 13При решении задачи по длинам сторон треугольников вычисляют углы, используя формулы
Тогда по координатам исходных пунктов и вычисленным углам треугольников решением прямой или обратной геодезических засечек рассчитывают координаты точки Р.
Слайд 14Если в треугольнике известны все стороны, то используя теорему косинусов можно
Слайд 15На практике решение задачи удобно выполнять по преобразованным формулам, не требующим
Слайд 174. Полярный метод
Данный метод применяется при передаче топоцентрических координат (в государственной
Для снесения координат пункта наземной сети А на рабочий центр Р - место установки спутникового приемника способом полярной засечки (рис. 5) измеряют горизонтальный угол β1 и линию S1. Измеренные линии приводятся к горизонту.
Координаты т. Р вычисляют по формулам прямой геодезической задачи. Измерения на пункте В выполняют для контроля.
Слайд 18Рисунок 5 – Схема снесения координат пункта наземной сети на рабочий центр
Слайд 195. Метод треугольника
При привязке дополнительной точки Р к настенным знакам методом
Рисунок 6 – Схема привязки методом треугольника
Слайд 20Вычисление координат т.Р выполняют в следующей последовательности:
Находят углы γ1 и γ2
Контроль вычислений и измерений выполняют по формулам:
γ1 + γ2 + β = 180° ,
|d - dʹ| = 5 мм, где d – расстояние вычисленное по исходным координатам точек 1 и 2,
Слайд 212. Находят дирекционные углы сторон 1-2, 1-А, 2-А.
3. По формулам прямой
Исходные данные
Х1 = 7451,18×n(м); Y1 = 5326,34×n(м);
Х2 = 7451,32×n(м); Y2 = 5347,52×n(м);
l1 = 29,081×n(м); l2 = 29,382 ×n(м); β = 46°43ʹ59ʹʹ.
Слайд 226. Передача координат с вершины знака на землю
Задача возникает при необходимости
Вблизи пункта А (на отстоянии 100-200 м) закрепляют точку Р с расчетом, чтобы с нее были видны пункты А, В и точка полигонометрического хода М (рис. 7).
Рисунок 7 – Схема снесения координат с вершины знака на землю
Слайд 23Из точки Р разбивают два базиса для определения недоступного расстояния АР
Второй базис bʹ и углы при нем необходимы для контроля определения расстояния АР = d.
Слайд 24Задача решается в следующей последовательности:
По известным координатам пунктов А и В
Решением вспомогательных треугольников с базисами по теореме синусов дважды вычисляют недоступное расстояние АР = d:
где γ = 180° - (β1+ β1ʹ), γʹ = 180° - (β2+ β2ʹ).
Расхождение в значениях недоступного расстояния допускается в пределах точности измерения длин линий в полигонометрическом ходе (1/10000). За окончательное значение расстояния АР принимают среднее арифметическое.
Слайд 253. Вычисляют дирекционный угол линии АР. Для этого из треугольника АВР
Вычисляют вспомогательный угол ϕ:
ϕ = 180° - (δ + ε).
По дирекционному углу исходной стороны АВ и вспомогательному углу ϕ вычисляют дирекционный угол стороны АР.
Измеренный при точке Р угол βР дает возможность определить дирекционный угол стороны РМ.
4. По длине стороны АР и дирекционному углу АР решением прямой геодезической задачи находим координаты т.Р.
Слайд 26Контроль измерений и вычислений выполняют одним из следующих способов.
Из треугольника АВР
αВР = αАР + δ и ее длину dBP = d(sinϕ/sinε).
Повторно рассчитывают координаты т.Р относительно пункта В.
2. По координатам т.Р и пункта В решением обратной геодезической задачи определяют дирекционный угол ВР и вычисляют угол δ как разность дирекционных углов сторон РВ и РА.
Допустимое расхождение Δδ = |δвыч - δизм|≤2mβ.
Слайд 27Оценка точности определения положения точки Р. Абсолютную СКП определения недоступного расстояния
СКП положения точки Р находят по формуле: