- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Миграция Столта презентация
Содержание
- 1. Миграция Столта
- 2. Определение миграции Процедура обработки сейсморазведочных данных, которая
- 3. Основные операции при миграции Миграция увеличивает крутизну
- 5. Миграция Столта (F-K миграция) Алгоритм: Входные данные
- 6. Математические основы Двумерное преобразование Фурье Решения скалярного волнового уравнения Миграция в области F-K
- 7. Двумерное преобразование Фурье
- 8. Свойство f-k преобразования Сигналы с одним и
- 9. Решение скалярного волнового уравнения
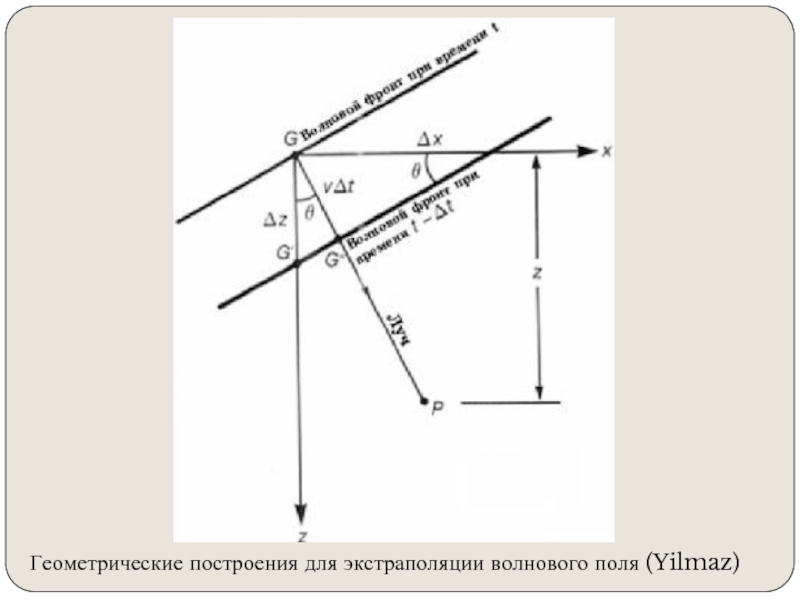
- 10. Геометрические построения для экстраполяции волнового поля (Yilmaz)
- 11. Уравнение миграции Stolt с постоянной скоростью
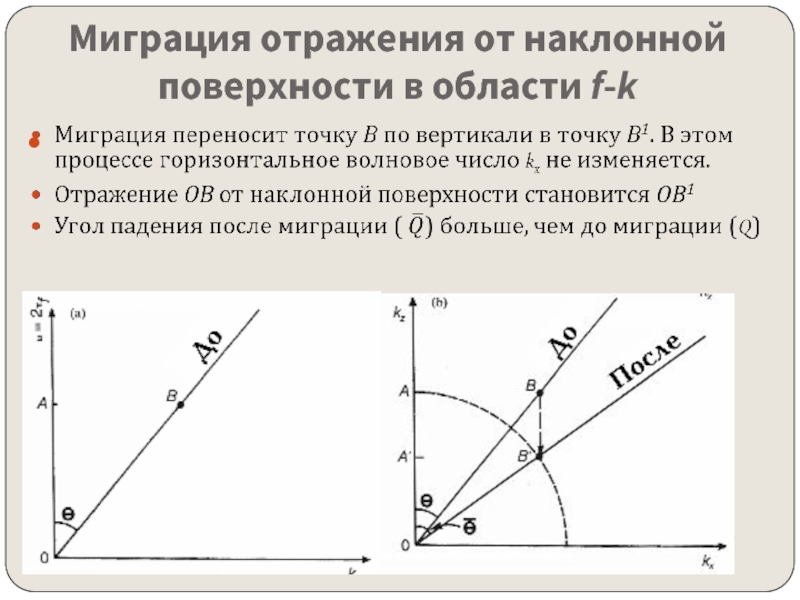
- 12. Миграция отражения от наклонной поверхности в области f-k
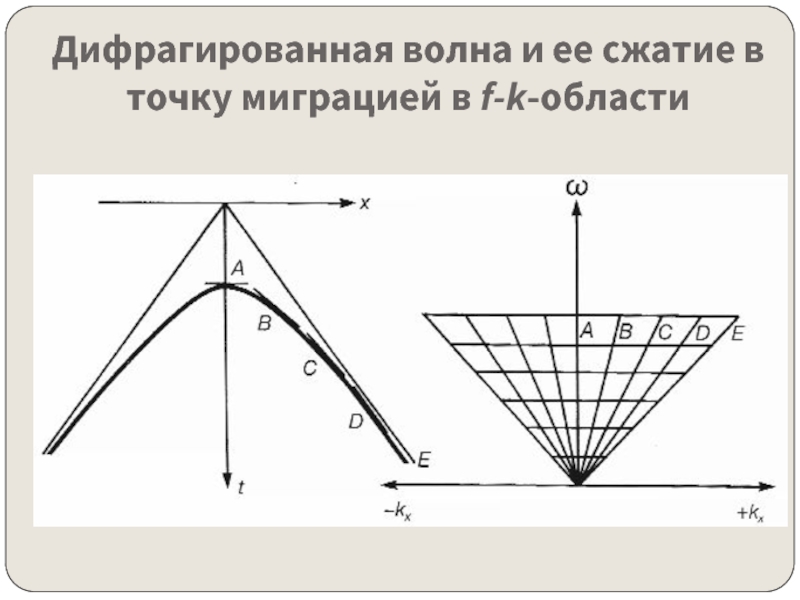
- 13. Дифрагированная волна и еe сжатие в точку миграцией в f-k-области
- 14. Миграция дифрагированной волны в областях (t,x) и (f,k) (в теории)
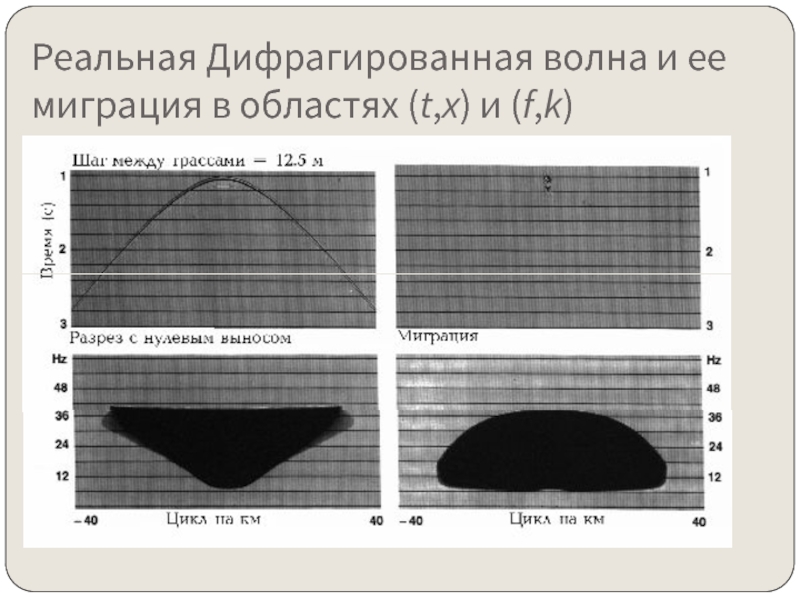
- 15. Реальная Дифрагированная волна и ее миграция в областях (t,x) и (f,k)
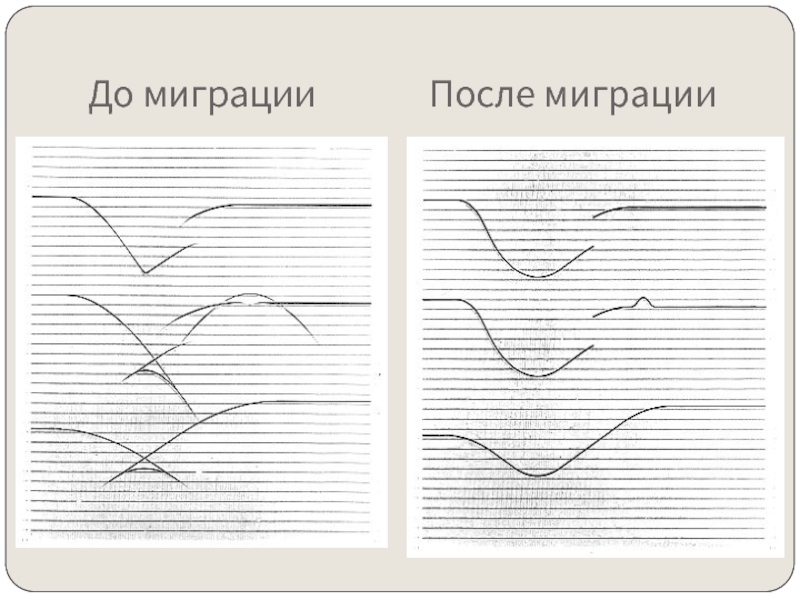
- 16. До миграции После миграции
- 17. Уравнение миграции Stolt в случае изменяющейся скорости
- 18. Преобразование координат
- 19.
- 20.
- 21. Миграция Столта на практике Метод Stolt может
- 22. Использование различных W
- 23. Суммарный разрез после введения статических поправок и
- 24. До миграции
- 25. После миграции
- 26. Список литературы Chun, Jacewitz - fundamentals of
- 27. Вопросы к зачету Каким образом осуществляется переход
- 28. Спасибо за внимание!
Определение миграции Процедура обработки сейсморазведочных данных, которая заключается в том, чтобы итоговый мигрированнный сейсмический разрез выглядел так же, как геологический разрез по профилю сьемки. Миграция перемещает наклонные отражающие поверхности в
Слайд 2Определение миграции
Процедура обработки сейсморазведочных данных, которая заключается в том, чтобы итоговый
мигрированнный сейсмический разрез выглядел так же, как геологический разрез по профилю сьемки.
Миграция перемещает наклонные отражающие поверхности в их истинные положения в разрезе и сжимает дифрагированные волны, тем самым подчеркивая элементы разреза (разломы, внедрения и т.д.)
(Yilmaz, seismic data processing)
Миграция перемещает наклонные отражающие поверхности в их истинные положения в разрезе и сжимает дифрагированные волны, тем самым подчеркивая элементы разреза (разломы, внедрения и т.д.)
(Yilmaz, seismic data processing)
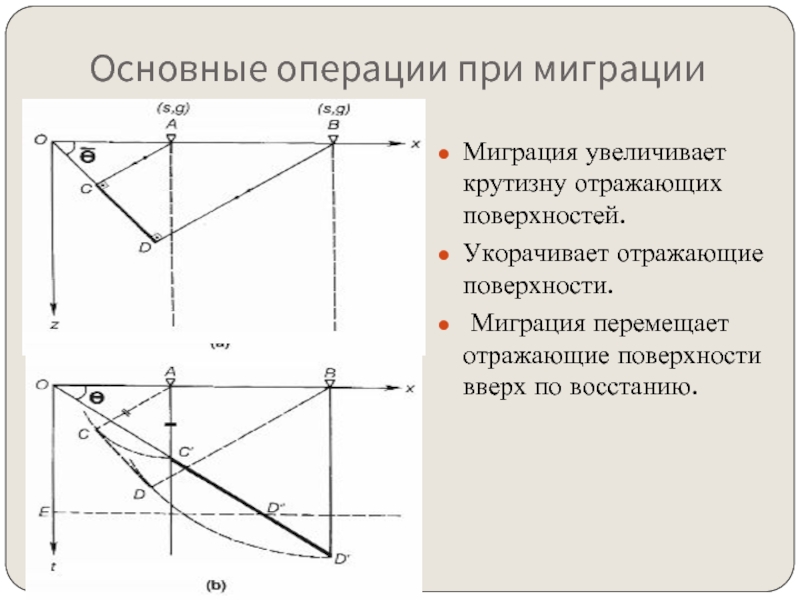
Слайд 3Основные операции при миграции
Миграция увеличивает крутизну отражающих поверхностей.
Укорачивает отражающие поверхности.
Миграция
перемещает отражающие поверхности вверх по восстанию.
Слайд 5Миграция Столта (F-K миграция)
Алгоритм:
Входные данные – сейсмический разрез с нулевым выносом.
Двумерное преобразование Фурье предполагает переход от осей t-х к осям f-k, где f- частота, k - волновое число
Слайд 6Математические основы
Двумерное преобразование Фурье
Решения скалярного волнового уравнения
Миграция в области F-K
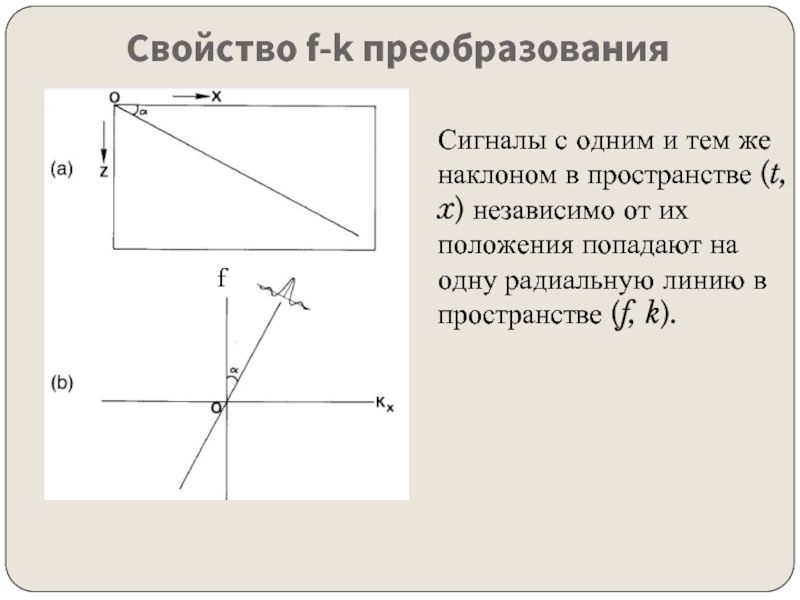
Слайд 8Свойство f-k преобразования
Сигналы с одним и тем же наклоном в пространстве
(t, x) независимо от их положения попадают на одну радиальную линию в пространстве (f, k).
Слайд 17Уравнение миграции Stolt в случае изменяющейся скорости
Задача: распространить алгоритм на случай
изменяющейся скорости без потери эффективности
Решение: преобразование координат, которое включает растяжение оси времен таким образом, чтобы волновое уравнение было не зависимым от скорости
Решение: преобразование координат, которое включает растяжение оси времен таким образом, чтобы волновое уравнение было не зависимым от скорости
Слайд 21Миграция Столта на практике
Метод Stolt может быть распространен на случай среды
с произвольной скоростью с помощью W – коэффициента растяжения Stolt. Теоретически W изменяется от 0 до 2.
W =1 соответствует алгоритму Stolt с постоянной скоростью
W<1, импульсный отклик сжимается вовнутрь вдоль его сильно наклоненных флангов;
при W>1 импульсный отклик раскрывается.
W =1 соответствует алгоритму Stolt с постоянной скоростью
W<1, импульсный отклик сжимается вовнутрь вдоль его сильно наклоненных флангов;
при W>1 импульсный отклик раскрывается.
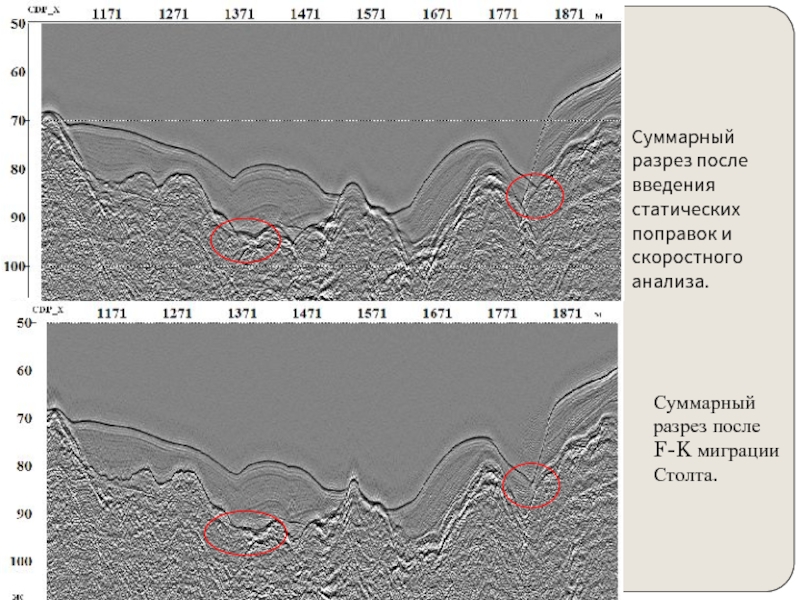
Слайд 23Суммарный разрез после введения статических поправок и скоростного анализа.
Суммарный разрез
после F-K миграции Столта.
Слайд 26Список литературы
Chun, Jacewitz - fundamentals of frequency-domain migration
Yilmaz, seismic data processing
Stolt
Seismic Imaging and Inversion
Слайд 27Вопросы к зачету
Каким образом осуществляется переход в F-K область?
Операции для получения
мигрированного разреза методом Stolt
Как осуществляется преобразование дифрагированных волн?
Как осуществляется преобразование дифрагированных волн?
