- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Гидрологические расчеты. Расчет расходов воды половодья и дождевых паводков ( Лекция 2) презентация
Содержание
- 1. Гидрологические расчеты. Расчет расходов воды половодья и дождевых паводков ( Лекция 2)
- 2. Основные темы лекции: Расчет максимальных расходов воды
- 3. Расчет максимальных расходов воды весеннего половодья и
- 4. Общая схема расчета максимальных расходов воды включает следующие этапы: © А. В. Сикан РГГМУ
- 5. На этом этапе производится: Этап 1.
- 6. Анализ хронологических графиков Ряд без видимых аномалий.
- 7. (1) (2) (3)
- 8. (1) (2) (3) Коэффициент автокорреляции незначим если
- 9. Коэффициент автокорреляции статистически незначим r(1) = -
- 10. (2) (1) (3) (4) Уильям Сили Госсет
- 11. (|t*| = 3,16) > (t2α=5% = 2,01).
- 12. Критерии однородности, используемые при наличии экстремальных значений,
- 13. Если выполняются неравенства (3) и (6) нулевая
- 14. Этап 4. Расчет параметров распределения Обычно рассчитываются
- 15. Для распределения Крицкого-Менкеля расчет оценок параметров распределения
- 16. Графический и графоаналитический методы в практике инженерных
- 17. Расчет параметров распределения с учетом исторического максимума
- 18. Определение исторического максимального расхода по установленному уровню
- 19. для метода моментов
- 20. Этап 5. Расчет погрешностей параметров распределения Формула
- 21. Этап 6. Построение эмпирической и аналитической кривых
- 22. Для наибольшего (или наименьшего) члена ряда наблюдений
- 23. Вопросы для самопроверки Общая схема расчета максимальных
- 24. © А. В. Сикан РГГМУ Владимиров А.М.
Слайд 1к.г.н., доц. Сикан Александр Владимирович
Российский государственный гидрометеорологический университет
Гидрологические расчеты
Часть II
лекция №
Слайд 2Основные темы лекции:
Расчет максимальных расходов воды весеннего половодья и дождевых паводков
Общая схема расчета максимальных расходов воды.
Учет выдающихся максимумов при расчете максимальных расходов воды.
Построение доверительного интервала для наибольшего члена ряда наблюдений.
© А. В. Сикан РГГМУ
Слайд 3Расчет максимальных расходов воды весеннего половодья и дождевых паводков при наличии
© А. В. Сикан РГГМУ
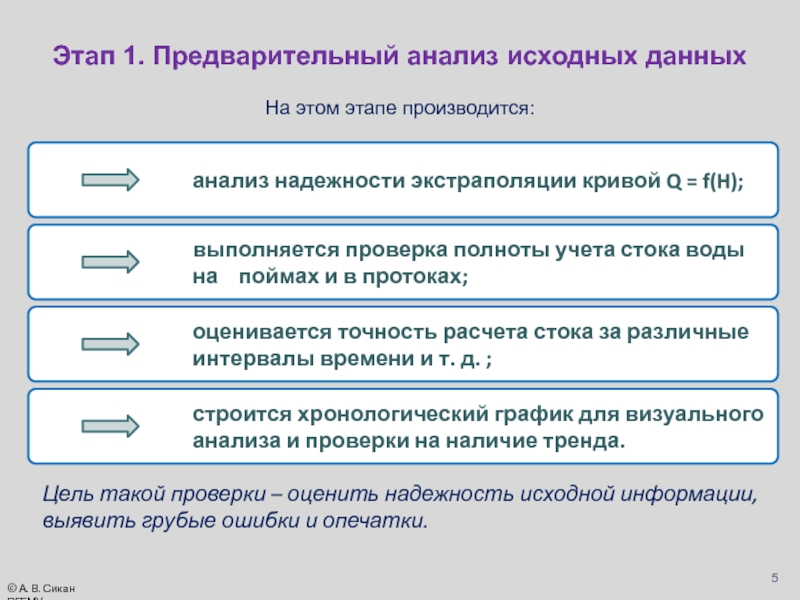
Слайд 5На этом этапе производится:
Этап 1. Предварительный анализ исходных данных
Цель такой
© А. В. Сикан РГГМУ
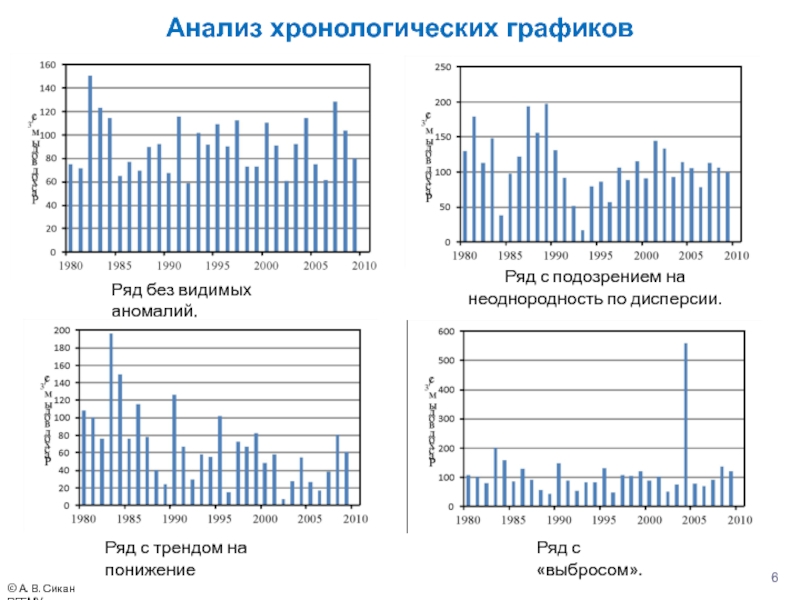
Слайд 6Анализ хронологических графиков
Ряд без видимых аномалий.
Ряд с подозрением на неоднородность по
Ряд с трендом на понижение
Ряд с «выбросом».
© А. В. Сикан РГГМУ
Слайд 7
(1)
(2)
(3)
(4)
Оценка значимости линейного тренда для зависимости
1-й вариант
2-й вариант
Тренд незначим если
где:
Тренд
где:
© А. В. Сикан РГГМУ
Слайд 8(1)
(2)
(3)
Коэффициент автокорреляции незначим если
Этап 2. Проверка ряда на случайность
В подавляющем большинстве
© А. В. Сикан РГГМУ
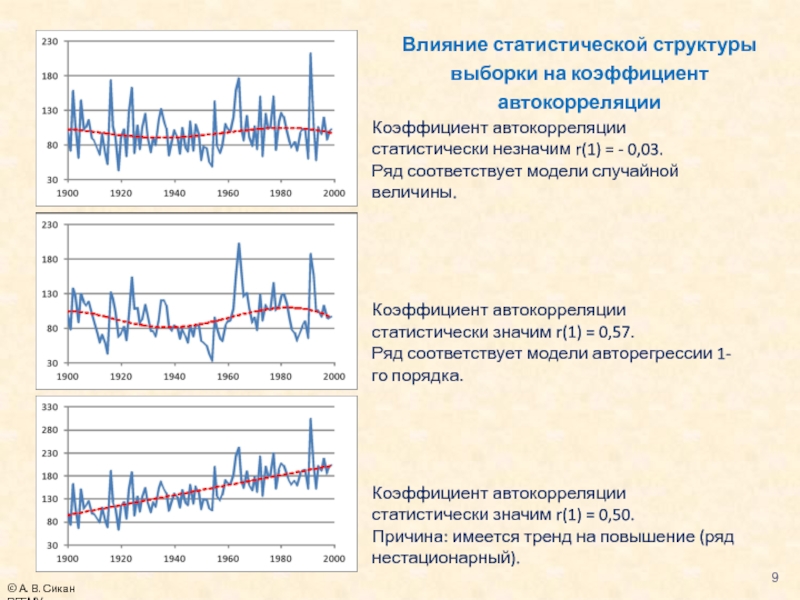
Слайд 9Коэффициент автокорреляции статистически незначим r(1) = - 0,03.
Ряд соответствует модели случайной
Коэффициент автокорреляции статистически значим r(1) = 0,57.
Ряд соответствует модели авторегрессии 1-го порядка.
Коэффициент автокорреляции статистически значим r(1) = 0,50.
Причина: имеется тренд на повышение (ряд нестационарный).
Влияние статистической структуры выборки на коэффициент автокорреляции
© А. В. Сикан РГГМУ
Слайд 10(2)
(1)
(3)
(4)
Уильям Сили Госсет Псевдоним – Стьюдент.
Английский ученый-статистик.
(1878-1937)
Рональд Эйлмер Фишер
Английский статистик и
(1890-1962)
Этап 3. Проверка ряда на однородность
Проверка однородности гидрологического ряда по дисперсии (критерий Фишера)
Проверка однородности гидрологического ряда по среднему значению (критерий Стьюдента)
Гипотеза об однородности ряда не опровергается, если выполняются неравенства (2) и (4).
© А. В. Сикан РГГМУ
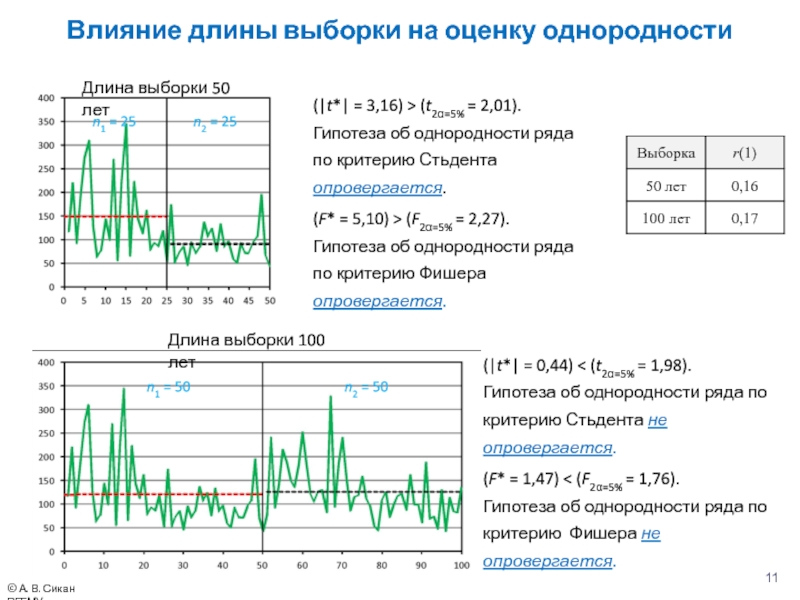
Слайд 11(|t*| = 3,16) > (t2α=5% = 2,01).
Гипотеза об однородности ряда по
(F* = 5,10) > (F2α=5% = 2,27).
Гипотеза об однородности ряда по критерию Фишера опровергается.
(|t*| = 0,44) < (t2α=5% = 1,98).
Гипотеза об однородности ряда по критерию Стьдента не опровергается.
(F* = 1,47) < (F2α=5% = 1,76).
Гипотеза об однородности ряда по критерию Фишера не опровергается.
Длина выборки 100 лет
Длина выборки 50 лет
Влияние длины выборки на оценку однородности
n1 = 25
n2 = 25
n1 = 50
n2 = 50
© А. В. Сикан РГГМУ
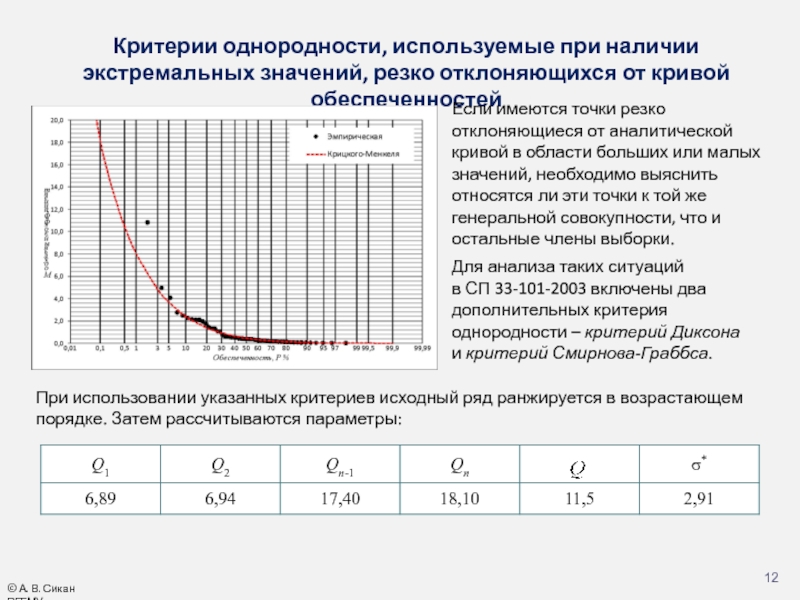
Слайд 12Критерии однородности, используемые при наличии экстремальных значений, резко отклоняющихся от кривой
Если имеются точки резко отклоняющиеся от аналитической кривой в области больших или малых значений, необходимо выяснить относятся ли эти точки к той же генеральной совокупности, что и остальные члены выборки.
Для анализа таких ситуаций
в СП 33-101-2003 включены два дополнительных критерия однородности – критерий Диксона
и критерий Смирнова-Граббса.
При использовании указанных критериев исходный ряд ранжируется в возрастающем порядке. Затем рассчитываются параметры:
© А. В. Сикан РГГМУ
Слайд 13Если выполняются неравенства (3) и (6) нулевая гипотеза об однородности ряда
Теоретические значения статистик Dα и Gα определяются по таблицам в зависимости от уровня значимости α, коэффициента автокорреляции r(1), коэффициента асимметрии Cs и длины ряда n.
Проверка однородности гидрологического ряда по критерию Диксона
Проверка однородности гидрологического ряда по критерию Смирнова-Граббса
© А. В. Сикан РГГМУ
Слайд 14Этап 4. Расчет параметров распределения
Обычно рассчитываются среднее значение ряда, коэффициент вариации
Если коэффициент вариации больше 0,6, следует произвести уточнение указанных характеристик, используя метод наибольшего правдоподобия.
© А. В. Сикан РГГМУ
Слайд 15Для распределения Крицкого-Менкеля расчет оценок параметров распределения производится в два этапа:
Рассчитываются вспомогательные статистики λ2 и λ3:
В зависимости от λ2 и λ3 по номограммам определяются значения Cv и Cs/Cv .
Метод наибольшего правдоподобия
© А. В. Сикан РГГМУ
Слайд 16Графический и графоаналитический методы в практике инженерных расчетов рассматриваются как вспомогательные.
В
Графический метод обычно применяют для подбора отношения коэффициента асимметрии к коэффициенту вариации, используя набор спрямляющих клетчаток
© А. В. Сикан РГГМУ
Слайд 17Расчет параметров распределения с учетом исторического максимума
При определении расчетных максимальных расходов
Сведения об исторических уровнях могут быть получены путем:
изучения меток высоких вод,
опроса населения,
сбора архивных материалов.
© А. В. Сикан РГГМУ
Слайд 18Определение исторического максимального расхода по установленному уровню осуществляется путем экстраполяции кривой
На основании проведенных исследований получают сам исторический максимум – QN
и продолжительность периода, в течение которого он не превышался – N.
Возможна и другая ситуация, когда в состав ограниченного ряда наблюдений за n лет входит выдающийся максимум. На кривой обеспеченности такой максимум отклоняется вправо относительно кривой, соответствующей основной массе расходов.
В этом случае исторический максимум известен, а период его непревышения (N) устанавливается путем опроса населения и сбора архивных материалов.
В Своде правил СП 33-101-2003 даны формулы (см. п.5.16), позволяющие уточнить значения параметров распределения с учетом исторического максимума.
© А. В. Сикан РГГМУ
Слайд 20Этап 5. Расчет погрешностей параметров распределения
Формула
Крицкого-Менкеля:
Формула Резниковского:
© А. В. Сикан
Слайд 21Этап 6. Построение эмпирической и аналитической кривых обеспеченностей
Эмпирическую ежегодную вероятность превышения
Для сглаживания и экстраполяции эмпирических кривых обеспеченностей, как правило, применяют трехпараметрические распределения:
Крицкого-Менкеля при любом отношении Cs/Cv
Пирсона III типа при Cs/Cv ≥ 2
Трехпараметрическое логнормальное распределение при Cs ≥ (3Cv + Cv3)
При неоднородности ряда гидрометрических наблюдений допускается применение усеченных и составных кривых распределения вероятностей.
© А. В. Сикан РГГМУ
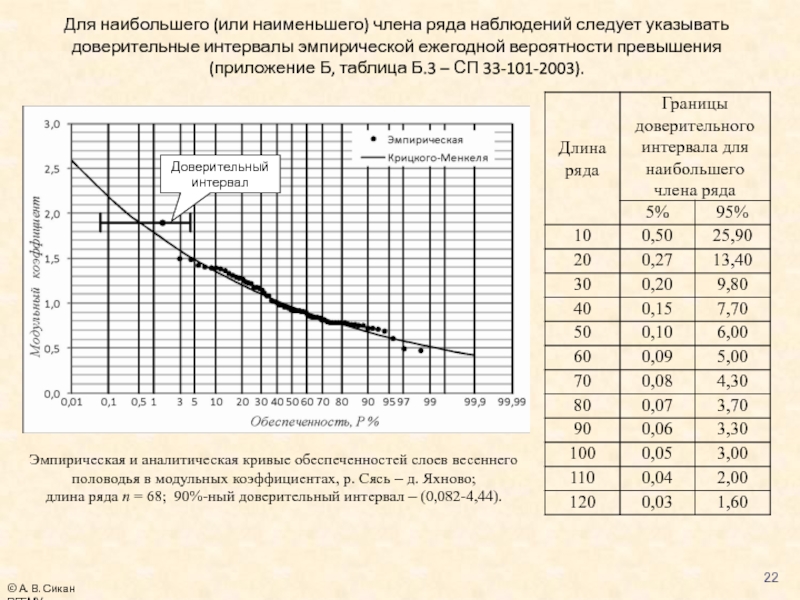
Слайд 22Для наибольшего (или наименьшего) члена ряда наблюдений следует указывать доверительные интервалы
Эмпирическая и аналитическая кривые обеспеченностей слоев весеннего половодья в модульных коэффициентах, р. Сясь – д. Яхново;
длина ряда n = 68; 90%-ный доверительный интервал – (0,082-4,44).
© А. В. Сикан РГГМУ
Слайд 23Вопросы для самопроверки
Общая схема расчета максимальных расходов воды. Перечислите основные этапы.
Какие
Какие методы используются при расчете статистических характеристик максимального стока?
Какова допустимая погрешность определения среднего значения и коэффициента вариации при расчетах максимального стока?
Какие типы кривых обеспеченностей наиболее часто используются в Российской гидрологической практике?
Как учитываются выдающиеся максимумы при расчетах максимальных расходов воды?
Как и с какой целью строится доверительный интервал для крайних членов выборки при расчете максимального стока?
© А. В. Сикан РГГМУ
Слайд 24© А. В. Сикан РГГМУ
Владимиров А.М. Гидрологические расчёты: п.9.1-9.2.
Сикан А.В.
СП 33-101-2003. «Определение основных расчетных гидрологических характеристик»: п.5.1-5.7; п.5.16; 5.26-5.28.
Методические рекомендации по определению расчетных гидрологических характеристик при наличии данных гидрометрических наблюдений: п.1-6; п.9.
Рекомендуемые материалы для изучения:
Конец лекции №2