- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Зубчатые передачи презентация
Содержание
- 1. Зубчатые передачи
- 2. Зубчатые передачи Принцип действия зубчатой передачи основан
- 3. Основные параметры Меньшее из пары зубчатых колес
- 4. Применение Зубчатые передачи наиболее широко распространены во
- 5. Основные параметры При этом особенности косозубых колес
- 6. Основные параметры У передач
- 7. Контактные напряжения и контактная прочность Контактные напряжения
- 8. Контактные напряжения и контактная прочность При вращении
- 9. Критерии работоспособности и расчета Условия работы зуба
- 10. Критерии работоспособности и расчета Поломка зубьев .
- 11. Расчетная нагрузка За расчетную нагрузку принимают максимальную
- 12. Особенности расчета косозубых и шевронных цилиндрических передач
- 13. Особенности расчета косозубых и шевронных цилиндрических передач
- 14. Червячные передачи Червячная передача относится к передачам
- 15. Волновые механические передачи Волновая передача основана на
- 16. Кинематические параметры и принцип действия В простой
- 17. Фрикционные передачи и вариаторы
- 18. Общие сведения Фрикционная передача состоит из двух
- 19. Достоинства и недостатки Достоинства: простота конструкции; бесшумность
- 20. Классификация Фрикционные
- 21. Классификация Фрикционные передачи с постоянным передаточным
- 22. Классификация
- 23. Способы прижатия катков Способы прижатия
- 24. Основные факторы, определяющие качество фрикционной передачи
- 25. Основные кинематические, силовые и геометрические соотношения
- 26. При расчетах вариаторов вместо отношения диаметров колес
- 27. Для передачи фрикционной передачей окружной силы Ft
- 28. Ременная передача состоит из ведущего и ведомого
- 29. ПРОФИЛИ РЕМНЕЙ РЕМЕННЫХ ПЕРЕДАЧ
- 30. возможность передачи движения между валами,
- 31. значительные габаритные размеры; непостоянство передаточного
- 32. Зубчатая передача представляет собой передаточный механизм, звеньями
- 33. Высокий КПД, значение которого достигает 0,99;
- 34. КЛАССИФИКАЦИЯ ЗУБЧАТЫХ ПЕРЕДАЧ а – цилиндрическая
- 35. Цепная передача состоит
- 36. отсутствие проскальзывания ремня; компактность;
- 37. удлинение цепи в процессе эксплуатации;
Слайд 2Зубчатые передачи
Принцип действия зубчатой передачи основан на зацеплении пары зубчатых колес:
По
По расположению зубьев на колесах различают передачи: прямозубые; косозубые.
По форме профиля зуба различают: эвольвентные; круговые.
Слайд 3Основные параметры
Меньшее из пары зубчатых колес называют шестерней, а большее —
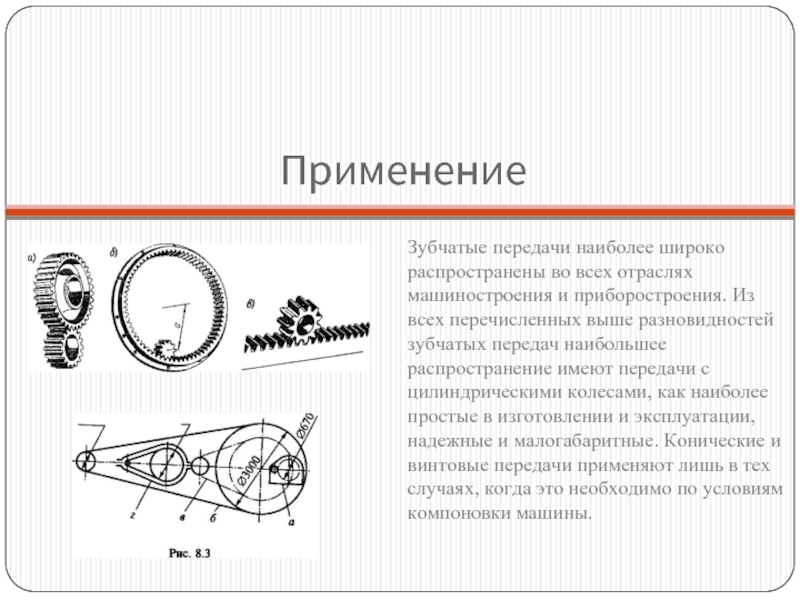
Слайд 4Применение
Зубчатые передачи наиболее широко распространены во всех отраслях машиностроения и приборостроения.
Слайд 5Основные параметры
При этом особенности косозубых колес рассматривают дополнительно: zx и z2
m = pin — окружной модуль зубьев (основная характеристика размеров зуба). Модули стандартизованы (ГОСТ 9563 — 80) в диапазоне 0,05...100 мм; d=pz/n = mz — делительный диаметр (диаметр окружности, по которой обкатывается инструмент при нарезании); db=dcosa, — основной диаметр (диаметр окружности, разверткой которой являются эвольвенты зубьев); dwl и dw2 — начальные диаметры (диаметры окружностей, по которым пара зубчатых колес обкатывается в процессе вращения):
dwi = 2aJ(z2/zi +1); dw2 = 2aw—dwl.
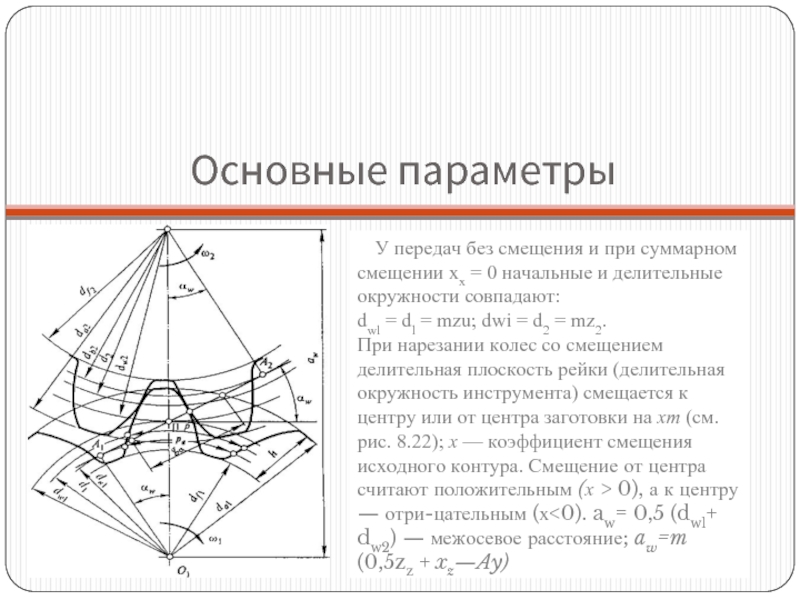
Слайд 6Основные параметры
У передач без смещения и при суммарном смещении хх =
dwl = dl = mzu; dwi = d2 = mz2.
При нарезании колес со смещением делительная плоскость рейки (делительная окружность инструмента) смещается к центру или от центра заготовки на хт (см. рис. 8.22); х — коэффициент смещения исходного контура. Смещение от центра считают положительным (х > 0), а к центру — отрицательным (х<0). aw= 0,5 (dwl+ dw2) — межосевое расстояние; aw=m (0,5zz + xz—Ay)
Слайд 7Контактные напряжения и контактная прочность
Контактные напряжения образуются в месте соприкосновения двух
Если контактные напряжения превышают величину допускаемого напряжения, то на поверхности деталей появляются вмятины, борозды, трещины или мелкие раковины.
При расчете контактных напряжений различают два характерных случая: первоначальный контакт в точке (два шара, шар и плоскость и т. п.); первоначальный контакт по линии (два цилиндра с параллельными осями, цилиндр и плоскость и т. п.).
На рис. 8.7 изображен пример сжатия двух цилиндров с
параллельными осями.
Слайд 8Контактные напряжения и контактная прочность
При вращении цилиндров под нагрузкой отдельные точки
Слайд 9Критерии работоспособности и расчета
Условия работы зуба в зацеплении. При передаче вращающего
Переменные напряжения являются причиной усталостного разрушения зубьев: поломка зубьев от напряжений изгиба и выкрашивание поверхности от контактных напряжений. С контактными напряжениями и трением в зацеплении связаны также износ, заедание и другие виды повреждения поверхностей зубьев.
Слайд 10Критерии работоспособности и расчета
Поломка зубьев . Поломка связана с напряжениями изгиба.
поломка от больших перегрузок ударного или даже статического действия (предупреждают защитой привода от перегрузок или учетом перегрузок при расчете);
усталостная поломка, происходящая от действия переменных напряжений в течение сравнительно длительного срока службы (предупреждают определением размеров из расчета на усталость). Особое значение имеют меры по устранению концентраторов напряжений (рисок от обработки, раковин и трещин в отливках, микротрещин от термообработки и т. п.).
Общие меры предупреждения поломки зубьев — увеличение модуля, положительное смещение при нарезании зубьев, термообработка, наклеп, уменьшение концентрации нагрузки по краям (жесткие валы, зубья со срезанными углами, бочкообразные зубья и пр.).
Повреждение поверхности зубьев. Все виды повреждения поверхности зубьев связаны с контактными напряжениями и трением.
Слайд 11Расчетная нагрузка
За расчетную нагрузку принимают максимальную величину удельной нагрузки, распределенной по
q=Fjqh,где F„ — нормальная сила в зацеплении; К= К^КрК, — коэффициент расчетной нагрузки; К^ — коэффициент распределения нагрузки между зубьями; Кр — коэффициент концентрации нагрузки; К, — коэффициент динамической нагрузки; h — суммарная длина линии контакта зубьев.
Концентрация нагрузки и динамические нагрузки различно влияют на прочность по контактным и изгибным напряжениям. Соответственно различают Кн= KHaKHpKHv — в расчетах по контактным напряжениям и KF=KFaKFpKFv — в расчетах по напряжениям изгиба.
Коэффициент распределения нагрузки между зубьями К^ определяется в зависимости от степени точности (п„) изготовления зубчатых колес по нормам плавности. Он учитывает влияние ошибок окружного шага и направления зубьев на величину в ненагружен- ной передаче. Для прямозубых передач:
Кш = 1 + 0,06 (лст— 5) < 1,25; для косозубых передач:
^«=1 + ^-5X1,6,
где С=0,15, если твердости поверхностей зубьев шестерни и колеса Я, и Я2 >350 НВ и С=0,25 при Я, и Я2<350 НВ или Я, >350 НВ, а Я2<350 НВ; 5<лст<9. В расчетах на прочность по напряжениям изгиба полагают KFa=KHa- Отметим, что для точно изготовленных передач («„=5) Кш = 1.
Слайд 12Особенности расчета косозубых и шевронных цилиндрических передач
Геометрические параметры. У косозубых колес
Индексы nut приписывают параметрам в нормальном и торцовом сечениях соответственно.
Прочность зуба определяют его размеры и форма в нормальном сечении. Форму косого зуба в нормальном сечении принято определять через параметры эквивалентного прямозубого колеса (рис. 8.25).
Слайд 13Особенности расчета косозубых и шевронных цилиндрических передач
Нормальное к зубу сечение косозубого
2„ = dvjm„ = dj{m„ cos2 /p)=m,z/(m, cos3 p), zv=z/cos3 p.
Слайд 14Червячные передачи
Червячная передача относится к передачам зацеплением с перекрещивающимися осями валов.
Слайд 15Волновые механические передачи
Волновая передача основана на принципе преобразования параметров движения за
Слайд 16Кинематические параметры и принцип действия
В простой передаче i равно отношению радиусов,
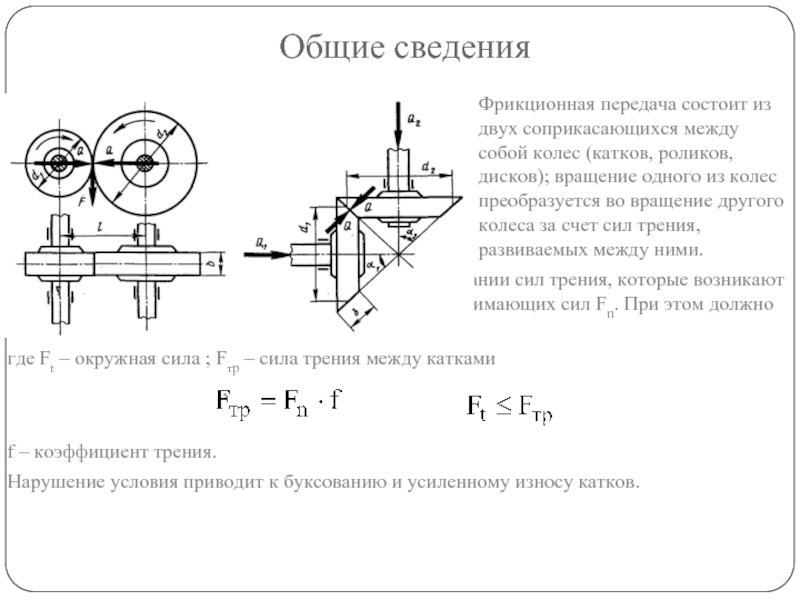
Слайд 18Общие сведения
Фрикционная передача состоит из двух соприкасающихся между собой колес (катков,
Работа фрикционной передачи основана на использовании сил трения, которые возникают в месте контакта двух тел вращения под действием сжимающих сил Fn. При этом должно быть
где Ft – окружная сила ; Fтр – сила трения между катками
,
f – коэффициент трения.
Нарушение условия приводит к буксованию и усиленному износу катков.
Слайд 19Достоинства и недостатки
Достоинства:
простота конструкции;
бесшумность работы;
равномерность вращения, что удобно для приборов;
возможность бесступенчатого
предохранение частей от поломок;
отсутствие мёртвого хода при реверсе передачи;
небольшая стоимость .
Недостатки:
потребность в прижимных устройствах;
значительные давления на валы и опоры;
повреждение катков при пробуксовке;
непостоянство передаточного числа из-за пробуксовки.
.
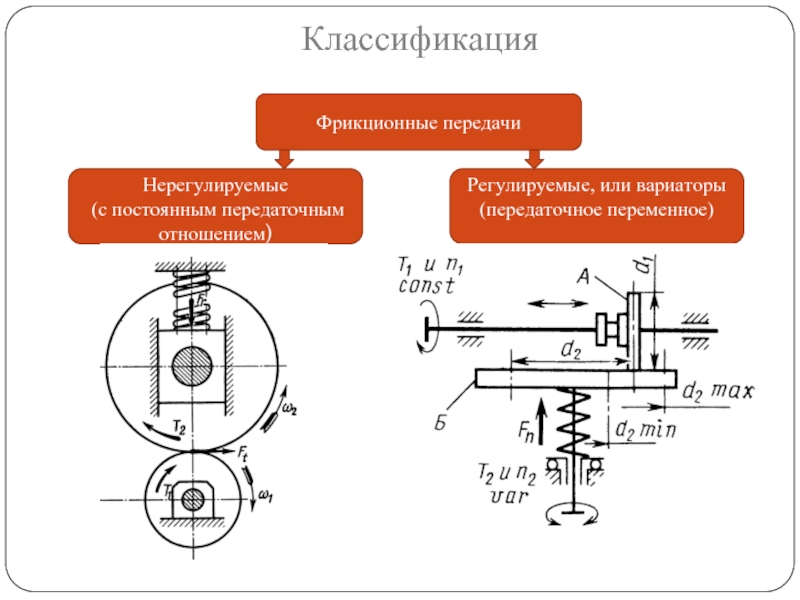
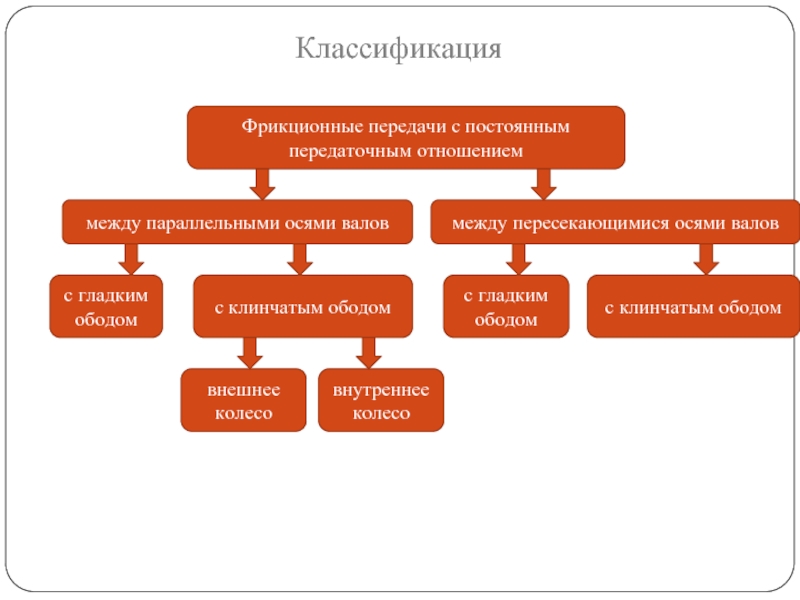
Слайд 20Классификация
Фрикционные передачи
Нерегулируемые
(с постоянным передаточным отношением)
Регулируемые, или вариаторы
(передаточное переменное)
Слайд 21Классификация
Фрикционные передачи с постоянным передаточным отношением
между параллельными осями валов
между пересекающимися осями
с гладким ободом
с клинчатым ободом
с гладким ободом
с клинчатым ободом
внешнее колесо
внутреннее колесо
Слайд 23Способы прижатия катков
Способы прижатия катков :
с постоянной силой ( вследствие
с переменной силой ( применением специальных нажимных устройств, например, шариковое самозатягивающее устройство, винтовое нажимное устройство ).
Способ прижатия катков оказывает большое влияние на качественные характеристики передачи :к.п.д., постоянство передаточного отношения, контактную прочность и износ катков. Лучшие показатели получают при регулируемом прижатии.
Слайд 24Основные факторы, определяющие качество фрикционной передачи
Скольжение является причиной износа, уменьшения к.п.д.
Различают три вида скольжения :
буксование;
упругое скольжение;
геометрическое скольжение.
Буксование наступает при перегрузках, когда не соблюдается условие Ft•Fтр. При буксовании ведомый каток останавливается, а ведущий скользит по нему, вызывая местный износ или задиры поверхности, что в конечном счете выводит передачу из строя. Поэтому при проектировании следует принимать достаточный запас сцепления k и не допускать использование фрикционной передачи в качестве предохранительного устройства от перегрузки.
Упругое скольжение связано с упругими деформациями в зоне контакта. Если бы катки были абсолютно жесткими, то первоначальный контакт по линии оставался бы таким и под нагрузкой. При этом окружные скорости будут равны и скольжения не будет. При упругих телах первоначальный контакт по линии переходит под нагрузкой в контакт по некоторой площадке.
Удлинение поверхности ведущего колеса, соприкасающейся с укорачивающейся поверхностью ведомого колеса, приводит к скольжению, которое начинается в точке 2, возрастает на участке 2-3 и в т.3 достигает максимального значения.
Геометрическое скольжение возникает на площадке контакта вдоль образующих колес, зависит от формы последних и связано с неравенством скоростей на площадке контакта у ведущего и ведомого катков. Оно является решающим для фрикционных передач.
Слайд 25Основные кинематические, силовые
и геометрические соотношения
В связи с проскальзыванием ведомого колеса
где ζ - [ дзета ] - коэффициент, учитывающий упругое скольжение (от 0,995 для передач, работающих всухую, до 0,95 – для вариаторов).
Можно записать оттуда
.
Для конической фрикционной передачи D1 и D2 – средние диаметры колес.
Таким образом, передаточное число фрикционной передачи с условно постоянным передаточным отношением
,
где η - коэффициент полезного действия передачи.
Для конической фрикционной передачи с углом взаимного расположения валов, равным 90°,
.
Для передач с постоянным передаточным отношением, работающих всухую, можно не учитывать коэффициент ζ. Тогда
и
.
Слайд 26При расчетах вариаторов вместо отношения диаметров колес D2/D1 принимают отношение их
Передаточное число вариатора изменяется от минимального Umin до максимального Umax значения.
Отношение максимальной угловой скорости ведомого колеса вариатора ω2max к минимальной его угловой скорости ω2min называется диапазоном регулирования
.
Для простых вариаторов, у которых радиус ведущего колеса остается постоянным, а радиус ведомого колеса изменяется в пределах от R2min до R2max
.
Диапазон регулирования в простых регуляторах D<4.
Для сдвоенных вариаторов при одновременном и симметричном изменении радиусов ведущего R1 и ведомого R2 колес
Диапазон регулирования в сдвоенных вариаторах D≤16.
Слайд 27Для передачи фрикционной передачей окружной силы Ft ее колеса должны прижиматься
,
где k – коэффициент запаса сцепления колес.
В силовых передачах машин k=1.25÷1.5, в передачах приборов k=2.5÷3.
Коэффициент трения между колесами :
для стали по стали в масле f=0.04÷0.05 ;
или чугуну в сухую f=0.15÷0.2.
Силы Fn1 и Fn2, действующие на валы конической фрикционной передачи с углом взаимного расположения валов, равным 90°
К.п.д. фрикционной передачи в зависимости от вида передачи может быть равен 0.7÷0.96. В основном, к.п.д. фрикционной передачи колеблется в пределах от 0.95÷0.96.
С целью уменьшения потерь и повышения η целесообразно увеличивать диаметры и сохранять постоянными во время работы передачи коэффициент тяги.
Последнее достигается применением механизмов, автоматически регулирующих усилие нажатия в зависимости от передаваемой окружной силы.
Слайд 28Ременная передача состоит из ведущего и ведомого шкивов, расположенных на расстоянии
Ременные передачи
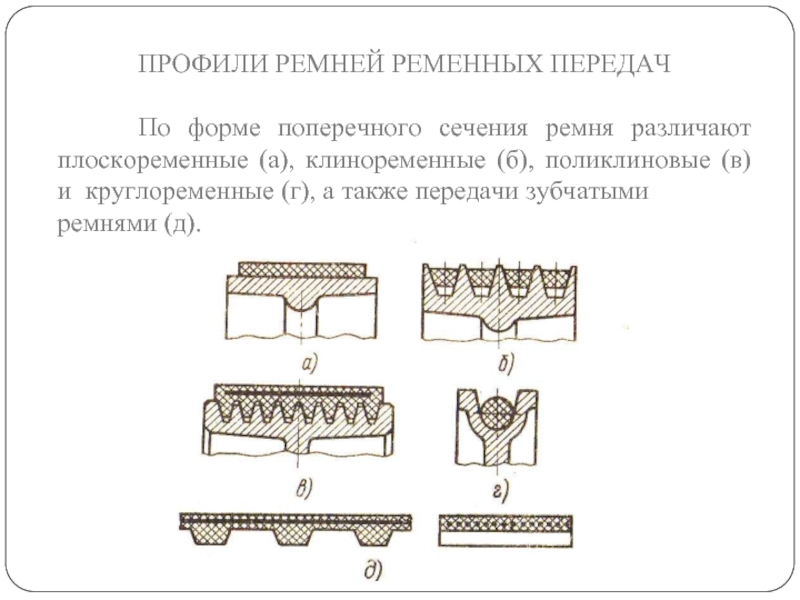
Слайд 29ПРОФИЛИ РЕМНЕЙ РЕМЕННЫХ ПЕРЕДАЧ
По форме поперечного сечения ремня
ремнями (д).
Слайд 30
возможность передачи движения между валами,
расположенными на значительном расстоянии;
плавность и
ограниченность передаваемой нагрузки;
простота конструкции;
лёгкость обслуживания;
небольшая стоимость изготовления.
Достоинства ременных передач
Слайд 31
значительные габаритные размеры;
непостоянство передаточного отношения из-за
проскальзывания ремня;
повышенное давление на
Недостатки ременных передач
Слайд 32Зубчатая передача представляет собой передаточный механизм, звеньями которого являются зубчатые колёса,
Зубчатые передачи
Слайд 33
Высокий КПД, значение которого достигает 0,99;
Возможность применения при окружных скоростях до
150 м/с для передачи мощностей от долей киловатт
до десятков тысяч киловатт;
высокая кинематическая точность;
точность изготовления;
надёжность и долговечность работы в различных
условиях эксплуатации.
Преимущество зубчатых передач
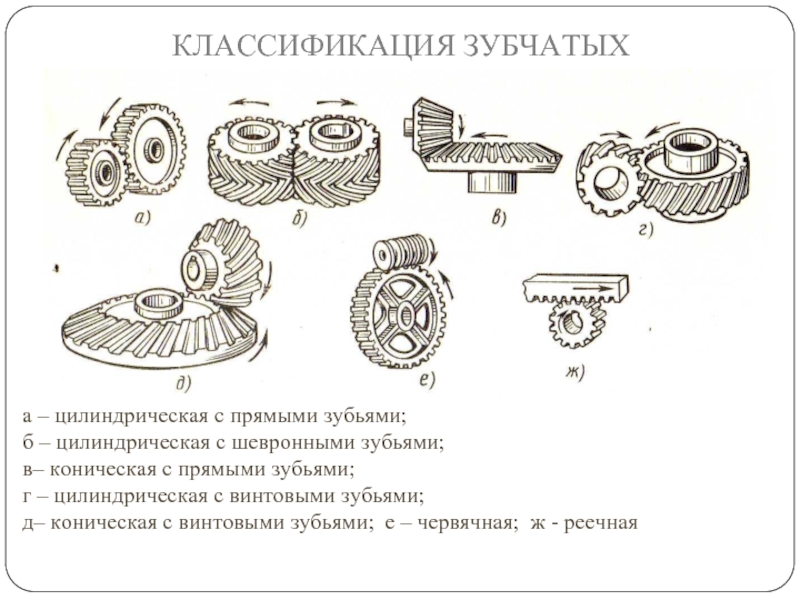
Слайд 34КЛАССИФИКАЦИЯ ЗУБЧАТЫХ ПЕРЕДАЧ
а – цилиндрическая с прямыми зубьями;
б – цилиндрическая
в– коническая с прямыми зубьями;
г – цилиндрическая с винтовыми зубьями;
д– коническая с винтовыми зубьями; е – червячная; ж - реечная
Слайд 35
Цепная передача состоит из двух, называемых
звёздочками, зубчатых
некотором расстоянии друг от друга и огибаемых цепью.
ЦЕПНЫЕ ПЕРЕДАЧИ
Слайд 36
отсутствие проскальзывания ремня;
компактность;
меньшая нагрузка на валы и подшипниковые
опоры, так
предварительного натяжения цепи;
высокий КПД, достигающий 0,98.
Достоинства цепных передач
Слайд 37
удлинение цепи в процессе эксплуатации;
возникновение динамических нагрузок в связи
с
шум при работе;
сложность эксплуатации.
Недостатки цепных передач